Ievads datoru arhitektūrā. 2 lekcija. Skaitļošanas sistēmas

1.

Ievads datoru arhitektūrā
DST203
2. lekcija
Skaitļošanas sistēmas
Asoc.prof. Dr.sc.ing. Dmitrijs Bļizņuks
1

2.

Saturs
Skaitliskās sistēmas: BIN HEX OCT
Pārveidošana starp sistēmām
Binārie skaitļi ar zīmi
Skaitļošanas operācijas: ADD SUB
MUL DIV
2

3.

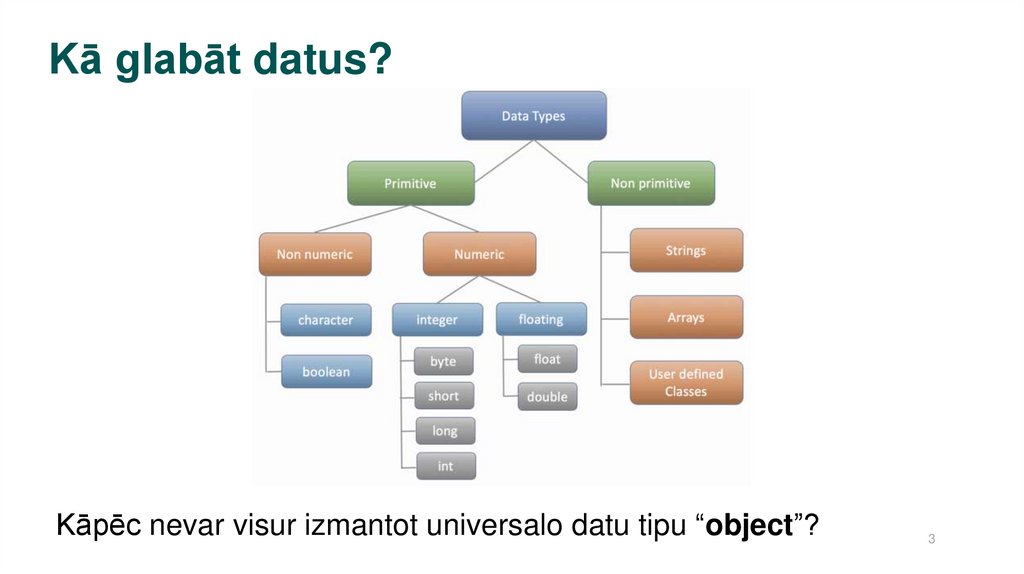
Kā glabāt datus?
Kāpēc nevar visur izmantot universalo datu tipu “object”?
3

4.

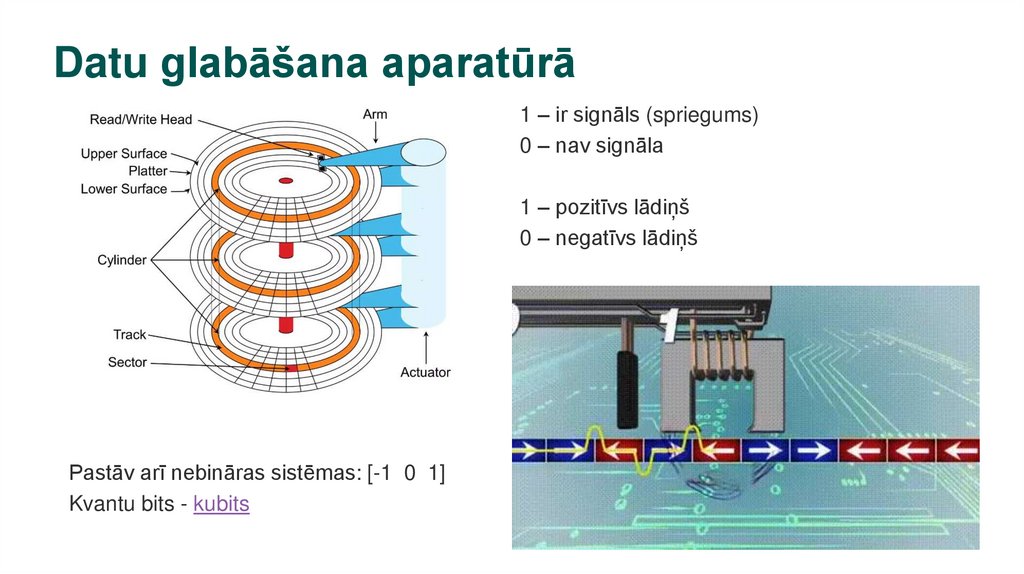
Datu glabāšana aparatūrā
1 – ir signāls (spriegums)
0 – nav signāla
1 – pozitīvs lādiņš
0 – negatīvs lādiņš
Pastāv arī nebināras sistēmas: [-1 0 1]
Kvantu bits - kubits
4

5.

Datu attēlošana
• Vizualizēšanas ērtība:
vai 6759813
• LV numurzīmju kombināciju skaits:
– Divi latiņu burti 262 un četri cipari 104 kopā 6 760 000
• Cik baitus jāatvēl universālam datu tipam?
• Kāpēc netiek izmantoti datu tipi attēls skaņa uc?
5
Rīgas Tehniskā universitāte

6.

Datu attēlošana
Maksimāls reālo objektu vienību skaits: mašīnas
personas. Pietiek ar vien 6-8 cipariem
Vēl lielāks?
Zinātniskie aprēķini (attālumi kosmosā molekulu
daudzums …) – 8 baiti 9223372036854775807
Laiks! 232 = 4 294 967 296 s >136 gadi
6
Rīgas Tehniskā universitāte

7.

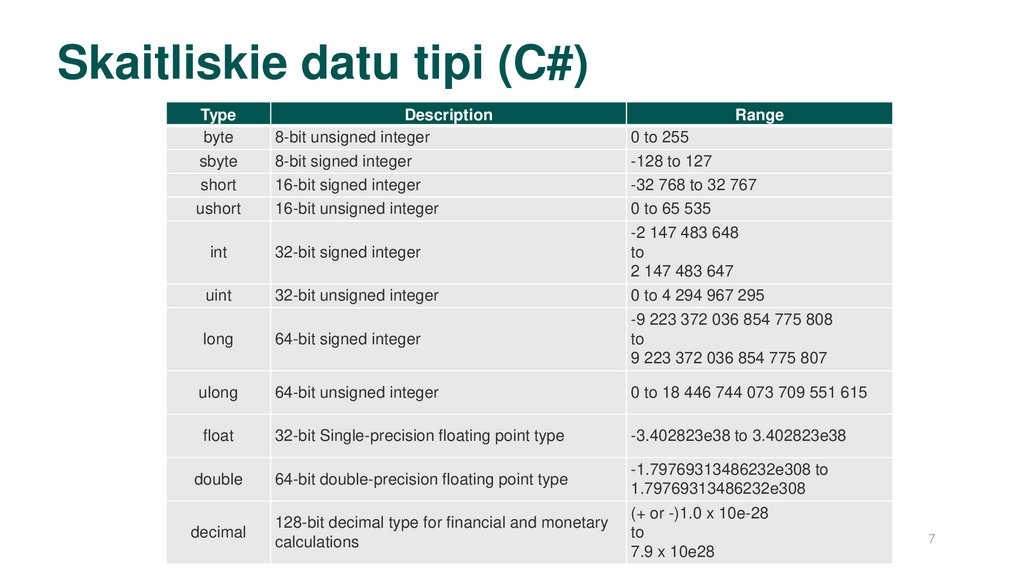
Skaitliskie datu tipi (C#)
Type
byte
sbyte
short
ushort
Description
8-bit unsigned integer
8-bit signed integer
16-bit signed integer
16-bit unsigned integer
Range
0 to 255
-128 to 127
-32 768 to 32 767
0 to 65 535
int
32-bit signed integer
-2 147 483 648
to
2 147 483 647
uint
32-bit unsigned integer
0 to 4 294 967 295
long
64-bit signed integer
-9 223 372 036 854 775 808
to
9 223 372 036 854 775 807
ulong
64-bit unsigned integer
0 to 18 446 744 073 709 551 615
float
32-bit Single-precision floating point type
-3.402823e38 to 3.402823e38
double
64-bit double-precision floating point type
-1.79769313486232e308 to
1.79769313486232e308
decimal
128-bit decimal type for financial and monetary
calculations
(+ or -)1.0 x 10e-28
to
7.9 x 10e28
7

8.

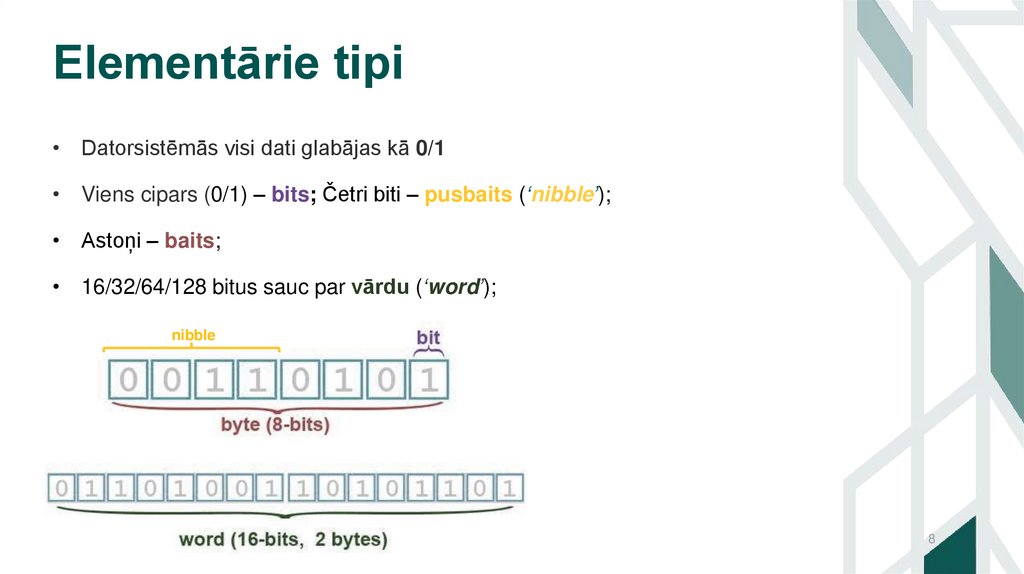
Elementārie tipi
• Datorsistēmās visi dati glabājas kā 0/1
• Viens cipars (0/1) – bits; Četri biti – pusbaits (‘nibble’);
• Astoņi – baits;
• 16/32/64/128 bitus sauc par vārdu (‘word’);
nibble
8

9.

Skaitļošanas sistēmu bāze
• Skaitļošanas sistēmas bāze norāda:
– Kā interpretēt katru ciparu
– Cik daudz ciparu ir iespējamas (0 1 2 3 4 5 6 7 8 9 A B C D E F)
• Kopējo vērtību var attēlot kā
a0*b0+b1*a1+b2*a2 +…+bn-1*an-1 +bn*an
kur “a” ir cipars “n” to pozīcija un “b” bāze
9

10.

• Heksadecimāla sistēma ir
tipiska neapstrādāto (‘raw’)
datu attēlošanai. Jo ir ērti
skatīt datus kur katrs baits ir
atdalīts;
• HEX
–
heksadecimālā
sistēma ar bāzi 16;
• Viens baits rakstāms ar
diviem simboliem.
• Piemēram: FF 10 2A.
10

11.

#AA00AA – fuchsia
AA 00
AA
170 0
170
red green blue
AA00AA (16) = 11141290 (10)
11141375 (10) = ?(16)
11

12.

12

13.

HEX uz DEC
Pārveidot no HEX uz DEC
– 1C216 = 2*160 + 12*161 + 1*162 = 2 + 192 + 256 = 45010
Alternatīvi – izmantojot tipiskās “apaļas” vērtības
– 10016 = 25610
– 20016 = 51210
– 30016 = 76810
Ļauj ātri pārveidot skaitļus, kuri ir tuvi apaļiem
– 20F16 = 20016 + F16 = 51210 + 1510 = 52710
– 1FF16 = 20016 - 116 = 51210 - 110 = 51110
13
13

14.

Patstāvīgi
12516 ? 10
40016 ? 10
7FFF16 ? 10
7FFFFFFF16 ? 10
14
14

15.

Rezultāti
12516 29310
40016 102410
7FFF16 3276710
7FFFFFFF16 214748364710
15
15

16.

DEC uz HEX
Princips – dalām ar bāzi un pierakstam atlikumu
1369510 ?16
– 13695:16=855*16 atlikums 1510 | F16
– 855:16=53*16
atlikums 710 | 716
No lejas uz augšu!
– 53:16=3*16
atlikums
510 | 516
– 3:16=0
atlikums
310 | 316
Rezultāts – 357F16
16
16

17.

Patstāvīgi
199910=?16
819210=?16
1638310=?16
17
17

18.

Rezultāti
199910=7CF16
819210=200016
1638310=3FFF16
18
18

19.

Pamatoperācijas
Operācijas notiek tāpat kā skolā ar desmitnieku sistēmu
167FD42
+ 256789
18D64CB
157FD43
- 456789
11295BA
DEC
HEX
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
A
11
B
12
C
13
D
14
E
15
F
19
19

20.

Negatīvas bināras vērtības
Ar n bināriem cipariem ir iespējams attēlot 2n kombinācijas kur
lielākais skaitlis ir 2n-1 skaitot no nulles. Lai attēlot negatīvas
vērtības ir jāpielieto zīmes kodēšanas principu.
Populārākie principi:
complement’)
skaitlis-zīme
un
papildkods
(‘two's
20
20

21.

Skaitlis-zīme
0000
+0
0001
+1
0010
+2
0011
+3
0100
+4
0101
+5
0110
+6
0111
+7
1000
-0
1001
-1
1010
-2
1011
-3
1100
-4
1101
-5
1110
-6
1111
-7
21

22.

Skaitlis-zīme
• Ir divas nulles +0 un -0 salīdzināšanā
jāignorē zīmi
• Nevar uzreiz veikt skaitliskās operācijas, jo
vecākais bits ir zīme
• Ērts cilvēkiem, nelietojams datorsistēmām
0000
+0
0001
+1
0010
+2
0011
+3
0100
+4
0101
+5
0110
+6
0111
+7
1000
-0
1001
-1
1010
-2
1011
-3
1100
-4
1101
-5
1110
-6
1111
-7
22

23.

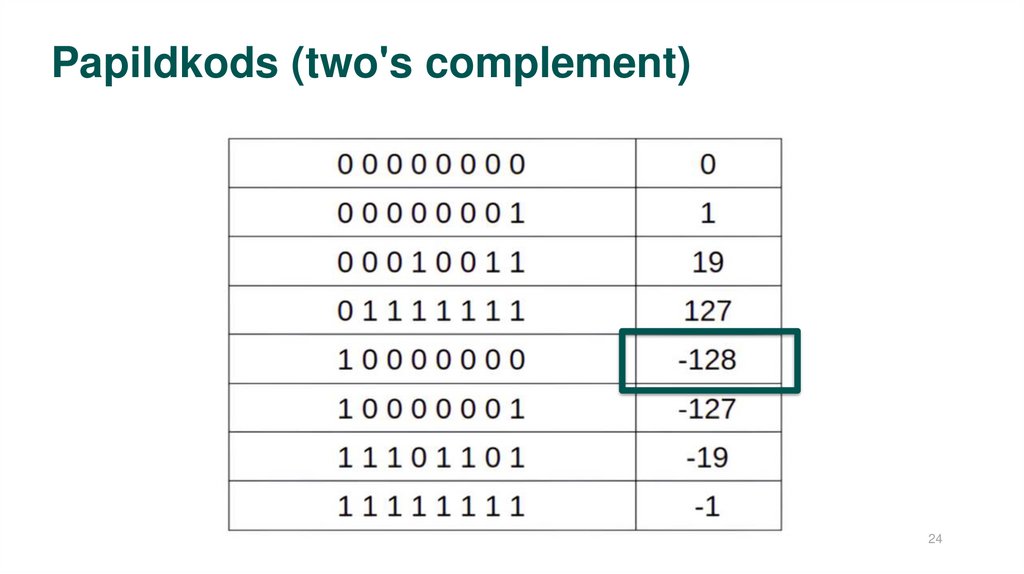
Papildkods (‘two's complement’)
• Viena nulle
• Var tieši operēt (saskaitīt, atņemt) ar
skaitļiem
• Pārveidošana notiek divos soļos:
invertēšana un +1 pieskaitīšana
• Negatīvo skaitļu ir par vienu vairāk
23

24.

Papildkods (two's complement)
24

25.

Bināra saskaitīšana
• Tāpat kā ar desmitnieku cipariem:
0+0=0
0+1=1
1+1=0 (papildus 1 tiek pārnests nākošā –
vecākā kartā)
• Operaciju rezultātā var notikt pārpilde (‘overflow’)
25

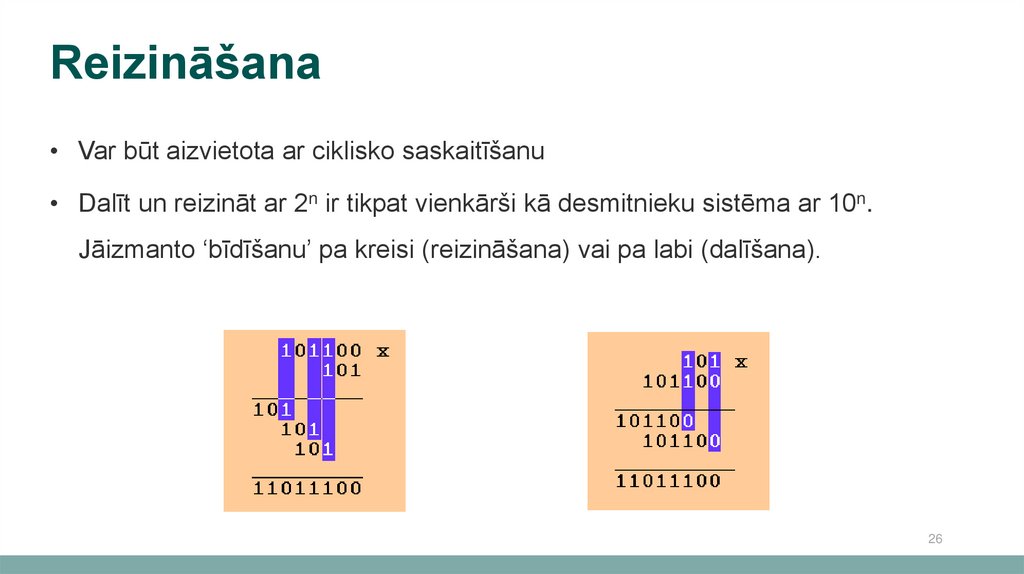
26.

Reizināšana
• Var būt aizvietota ar ciklisko saskaitīšanu
• Dalīt un reizināt ar 2n ir tikpat vienkārši kā desmitnieku sistēma ar 10n.
Jāizmanto ‘bīdīšanu’ pa kreisi (reizināšana) vai pa labi (dalīšana).
26

27.

Dalīšana
Desmitnieku sistēma
Heksadecimālā sistēma
27

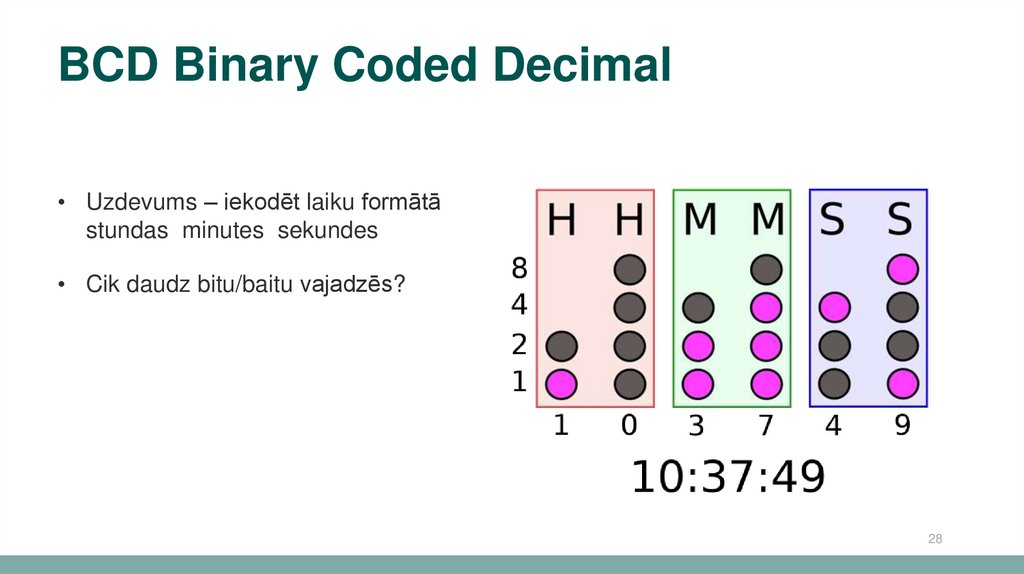
28.

BCD Binary Coded Decimal
• Uzdevums – iekodēt laiku formātā
stundas minutes sekundes
• Cik daudz bitu/baitu vajadzēs?
28

29.

Papildus materiāli
– http://en.wikipedia.org/wiki/Signed_number_representations
– http://en.wikipedia.org/wiki/Overflow_flag
– http://en.wikipedia.org/wiki/Multiplication_algorithm
– http://en.wikipedia.org/wiki/Division_(digital)
– http://en.wikipedia.org/wiki/Pentium_FDIV_bug
– http://en.wikipedia.org/wiki/Two's_complement
– http://en.wikipedia.org/wiki/Arithmetic_overflow
– http://en.wikipedia.org/wiki/Category:Computer_arithmetic
29
29