Похожие презентации:
Комбинаторика
1. КОМБИНАТОРИКА
Основные понятия, определения и решение задач.Составитель учитель математики МАОУ СОШ № 40
САЛИЙ ВАЛЕНТИНА ПАВЛОВНА
2. Что изучает комбинаторика?
• В науке и практике часто встречаются задачи, решаякоторые приходится составлять различные комбинации из
конечного числа элементов и подсчитывать число
комбинаций. Такие задачи получили название
комбинаторных задач, а раздел математики, в котором
рассматриваются подобные задачи, называют
комбинаторикой. Слово «комбинаторика» происходит от
латинского слова combinare, которое означает «соединять,
сочетать».
3. Пример 1
• Из группы теннисистов, в которую входят четыре человека– Антонов, Григорьев, Сергеев и Федоров, тренер
выделяет пару для участия в соревнованиях. Сколько
существует вариантов выбора такой пары?
4. Решение
• Составим сначала все пары, в которые входитАнтонов (для краткости будем писать первые
буквы фамилий). Получим три пары : АГ, АС, АФ.
Выпишем пары, в которые входит Григорьев, но
не входит Антонов : ГС, ГФ. Далее составим пары,
в которые входит Сергеев, но не входят Антонов и
Григорьев : СФ. Других вариантов нет. Итак,
получили шесть пар : АГ, АС, АФ,ГС,ГФ,СФ.
• Способ рассуждений, которым решена задача,
называют перебором возможных вариантов.
5. Пример 2
• Четыре ученика класса Миша, Саша,Алёша, Таня углублённо изучают
математику. На математическую
олимпиаду требуется послать двух
учеников. Сколькими способами это можно
сделать?
6.
7. Пример 3
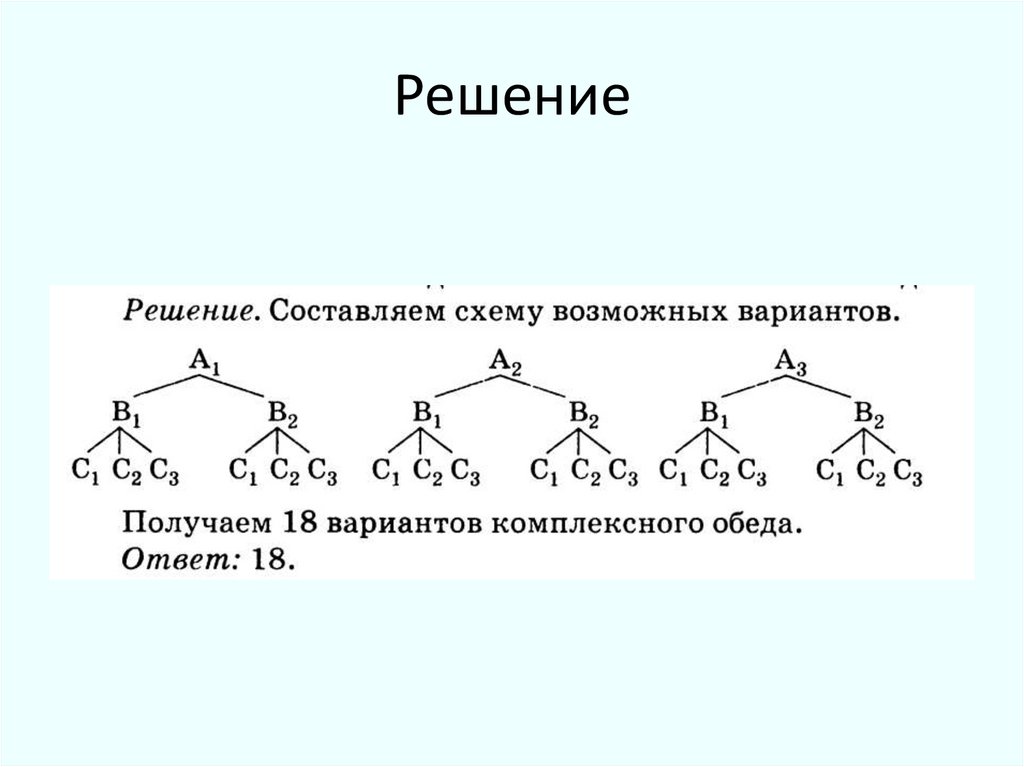
• В меню столовой три первых блюда А1 ,А2А3, два вторых В1, В2 и три сока С1, С2, С3.
Сколько вариантов комплексного обеда
можно составить из этих блюд?
8. Решение
9. Решите задачи
• №1 У Ирины пять подруг: Вера, Зоя, Марина,Полина и Светлана. Она решила двух из них
пригласить в кино. Укажите все возможные
варианты выбора подруг. Сколько таких
вариантов?
• №2 Стадион имеет четыре выхода: А, В, С,Д.
Укажите все возможные способы, какими
посетитель может войти через один выход , а
выйти через другой. Сколько таких способов?
10.
№3 Из цифр 1,2,3 составьте все возможныедвузначные числа при условии, что:
а) цифры в числе не повторяются;
б) допускается повторение цифр в числе.
11. Решение задач
• №1. ВЗ, ВМ, ВП, ВС; ЗМ,ЗП,ЗС; МП,МС; ПС.Всего 10 вариантов.
• №2 АВ, АС, АД; ВС, ВД,СД;
ВА,СА,ДА,СВ,ДВ,ДС. Всего12 вариантов.
• №3 а)12, 13, 23,21,31,32.
• б) 11,12,13,22,21,23,31.32,33.
12. Пример 4
• В посёлке имеется 5 светофоров. Каждыйможет находиться в одном из трёх
состояний (гореть красным, зелёным или
жёлтым светом). Сколькими способами
можно зажечь все светофоры?
13. Решение
• Первый светофор может быть включён тремяразными способами. Для каждого способа
включения первого светофора можно получить 3
способа включения второго светофора, т.е. будем
иметь 3 • 3 способов включения двух светофоров.
Из всякого способа включения двух светофоров
снова можно получить три способа включения
третьего светофора, изменяя его состояние, всего
получаем 3 • 3 • 3 способов включения трёх
светофоров. При включении каждого нового
светофора число способов увеличивается в три
раза. Значит, пять светофоров могут быть включены
3 • 3 • 3 • 3 • 3 = З5 способами. Ответ: 243 способа.
14. Правила сложения и умножение
• Задачи комбинаторики решаются проще,если использовать комбинаторные
правила сложения и умножения. Пусть
даны два непересекающихся множества
элементов: А ={a1 а2, ..,аn} и B ={Ь1, Ь2, .., Ьn }.
15. Правило сложения.
• Если элемент а(а ϵ А) может быть выбран nспособами, а элемент Ь(Ь ϵ В) может быть
выбран m способами, то число способов,
которыми можно выбрать один элемент из
множества А или множества B, равно сумме
n + m.
16. Пример 5
• В одном классе 25 учеников, в другом — 27учеников. Сколькими способами можно
выбрать одного ученика из двух классов?
17. Решение
• Решение. 25 + 27 = 52. Ответ: 52.18. Пример 6
• Для проезда из города М в город N можновоспользоваться 5 автобусными
маршрутами или 3 железнодорожными.
Сколькими способами можно проехать из
города М в город N?
19. Решение
• Решение. По формуле сложения количествоспособов равно сумме 5 + 3 = 8. Ответ: 8.
20. Правило умножения (основное правило комбинаторики).
• Если элемент а(а ϵ А) может быть выбран nспособами, а элемент b (b ϵ В) после
каждого выбора элемента а может быть
выбран m способами, то число способов,
которыми можно выбрать пару элементов а
и b в указанном порядке по одному из
каждого множества, равно произведению
n •m.
21. Пример 7
• В одном классе 25 учеников, в другом — 27учеников. Сколькими способами можно
выбрать двух учеников по одному из
каждого класса?
22. Решение
• Одного ученика первого класса можновыбрать 25 способами, а второго класса —
27 способами. Двух учеников по одному из
каждого класса (по правилу умножения)
можно выбрать 25 • 27 способами; 25 • 27
= 675. Ответ: 675.
23. Пример 8
• На книжной полке стоит 6 историческихроманов и 4 приключенческих. Сколькими
способами можно взять с полки 2 книги
разных жанров?
24. Решение
• По правилу умножения существует 6 • 4способов взять с полки 2 книги разных
жанров. Ответ: 24.
25. Правило умножения в общем виде.
• Пусть имеем n элементов, из которыхтребуется выбрать один за другим некоторые
k элементов. Если первый элемент можно
выбрать n1 способами, после чего второй
элемент можно выбрать n2 способами, затем
третий элемент — n3 способами и т.д., то число
способов, которыми могут быть выбраны все k
элементов, равно произведению
n1 • n2 • n3 • ... • nk.
26. Пример 9
• Собрание из 30 человек должно выбратьпредседателя и секретаря. Сколькими
способами это можно сделать?
27. Решение
• Председателем собрания можно выбрать30 способами, после чего секретаря — 29
способами (из 29 оставшихся членов
собрания). По правилу умножения
существует 30 • 29 способов выбора
председателя и секретаря. 30•29 = 870.
Ответ: 870.
28. Пример 10
• Сколькими способами можно рассадить 5гостей за праздничным столом, если
приготовлено 8 мест?
29. Решение
• Для первого гостя имеется 8 возможностейвыбрать место. После выбора места
первым, для второго гостя остаётся 7
возможностей, аналогично для третьего
гостя — 6 возможностей (из 6 свободных
мест), для четвёртого — 5 вариантов, для
пятого — 4. По правилу умножения
получаем 8 • 7 • 6 • 5 • 4 = 6720 способов
рассадить гостей. Ответ: 6720.
30. Пример 11
• Из 10 членов шахматного кружка требуетсясоставить команду из 3 человек для участия
в соревнованиях. Сколькими способами
это можно сделать?
31. Решение
• Первого члена команды (на первую доску)можно выбрать 10 способами, после чего
второго (на вторую доску) — 9 способами,
а третьего (на третью доску) — 8
способами. Всего получаем 10 • 9 • 8= 720
вариантов выбора трёх шахматистов из
десяти. Ответ: 720.
32. Перестановки
• Перестановкой называется конечноемножество, в котором установлен порядок
его элементов. Число перестановок из n
элементов обозначают символом Рn (от
французского слова permutation —
«перестановка»).
33. Формула для вычисления перестановок
• Число перестановок из n элементов равнопроизведению всех натуральных чисел от
1 до n;
• Рn = n!.
34. Пример 12
• Сколькими способами семья из 5 человекможет занять пять спальных мест в
пятиместном гостиничном номере?
35. Решение
• Р5=1 • 2 • 3 • 4 • 5 = 120.• Ответ: 120.
36. Пример 13
• Каким числом способов 8 человек могутнаходиться в очереди?
37. Решение
• Р8=1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 = 40 320.Ответ: 40 320.
38. Пример 14
• Сколько различных четырёхзначных чиселможно составить из цифр 9, 7, 5, 0, если в
каждом числе все цифры должны быть
разными?
39. Решение
• Если бы среди данных цифр не было нуля, токоличество составленных из них четырёхзначных
чисел (без повтора цифр в каждом числе) было бы
равно количеству перестановок из 4 элементов:
• Р4 = 1 • 2 • 3 • 4 = 24.
• Целое число не может начинаться цифрой 0. Среди
найденных 24 чисел с цифры 0 будет начинаться
столько чисел, сколько существует перестановок из
3 элементов (цифр 9, 7, 5): Р3 = 1 • 2 • 3 = 6.
• Значит, четырёхзначных чисел, составленных из
данных цифр, будет Р4 - Р3 = 24 - 6 = 18. Ответ: 18.
40. Пример 15
• 9 мальчиков купили 9 билетов в театр.Сколькими способами они могут занять 9
кресел в театральном ряду, если Миша,
Петя и Ваня обязательно хотят сидеть
рядом (в любом порядке).
41. Решение
• Будем считать трёх неразлучных друзей (Мишу, Петю и Ваню)как один элемент общей компании, а три занятых ими кресла —
как одно место. Тогда можем считать, что размещаем 7 человек
в 7 креслах. Это можно сделать столькими способами, каково
число перестановок из 7 элементов: Р7 =1 • 2 • 3 • 4 • 5 • 6 • 7 =
5040.
• В то же время трое друзей (Миша, Петя и Ваня) в своих трёх
креслах могут распределиться Р3 способами
• Р3 = 1 • 2 • 3 = 6.
• Таким образом, каждой перестановке из 7 элементов
соответствует любая перестановка из трёх элементов. Всего
перестановок по правилу умножения будет
• Р7 • Р3 = 5040 • 6 = 30 240.
• Ответ: 30 240.
42. Размещения
43. Обозначение
44. Формула для вычисления размещений
45. Пример 16
• Учащиеся класса изучают 11 различныхпредметов. Сколькими способами можно
составить расписание на один день, чтобы
в нём было 5 различных предметов?
46.
47. Пример 17
• Сколько четырёхзначных чисел можносоставить из нечётных цифр, если все
цифры в числе различны?
48.
49. Пример 18
• Сколькими способами 10 человек могутзанять четыре кресла, имеющиеся в
комнате?
50.
51. Пример 19
• В одиннадцатом классе 25 учащихся. Навыпускном вечере ребята обменялись друг
с другом фотокарточками. Сколько всего
было роздано фотокарточек?
52.
53. Сочетания
• Сочетанием из n элементов по k называетсялюбое множество, составленное из k
элементов, выбранных из данных п
элементов. В отличие от размещений,
сочетания различаются только элементами,
и не имеет значения, в каком порядке
заданы элементы.
• Например, {а, Ь, с} и {Ь, с, а} — одно и то же
сочетание.
54. Формула для вычисления сочетаний
55. Пример 20
• В вазе стоят 10 красных и 5 белых роз.• а) Сколькими способами можно составить
букет из 3 роз?
• б) Сколькими способами можно составить
букет из 1 красной и 2 белых роз?
56.
57. Пример 21
• Из 9 мальчиков и 11 девочек спортивногокласса для участия в соревнованиях надо
составить команду, в которую должны
входить 3 мальчика и 3 девочки.
Сколькими способами это можно сделать?
58. Решение
59. Пример 22
На витрине магазина выставлено 6 сортовсыра и 5 видов йогурта. Покупателю
требуется 2 куска сыра разных сортов и 3
йогурта разного вида. Сколькими
способами покупатель может составить
свою покупку?
60. Решение
61. Решите задачи
• 1. Для проезда из города М в город N можновоспользоваться 5 автобусными маршрутами или 3
железнодорожными. Сколькими способами можно
проехать из города М в город N?
• 2. Из города А в город С можно проехать лишь с
пересадкой в городе Б. Из А в Б существуют 3
автобусных маршрута и 2 железнодорожных. Из Б в С
можно проехать 4 поездами или 2 автобусами. Сколько
существует вариантов проезда из города А в город С?
• 3. Из 5 первокурсников, 7 второкурсников и 10
третьекурсников надо выбрать трёх студентов на
конференцию. Сколькими способами это можно
сделать, если студенты должны быть разных курсов?
62. Решение задач
• 1. По формуле сложения количествоспособов равно сумме 5 + 3 = 8. Ответ: 8.
• 2. Из А в Б можно проехать 3 + 2 = 5
способами, а из Б в С — 6 способами
(4 + 2 = 6). По формуле умножения из А в С
можно проехать 5 • 6 = 30 способами.
Ответ: 30.
• 3.По теореме умножения получаем 5•7•10
= 350 способов. Ответ: 350.
63. Решите задачи
• 4. Сколькими способами можно расставить наполке 10 различных книг?
• 5. На полке стоит 8 разных книг по математике и 2
разные книги по физике. Сколькими способами
можно расставить эти книги, если книги по физике
должны стоять рядом?
• 6. Сколькими способами можно расставить на
полке 7 различных книг так, чтобы определённые
три книги стояли рядом?
• 7. Сколькими способами можно расставить на
полке 7 различных книг, чтобы определённые 3
книги не стояли рядом?
64. Решение задач 4,5
• 4. Количество способов равно числу перестановокиз 10 элементов. Р10 = 10! = 1 • 2 • 3 • 4 • 5 • 6 • 7
8 • 9 • 10 = 3 628 800. Ответ: 3 628 800.
• 5. Будем рассматривать 2 книги по физике как одну
книгу. Тогда 9 книг можно расставить Р9 способами.
Далее 2 книги по физике можно в каждом случае
поставить двумя разными способами. По правилу
умножения общее количество вариантов равно 2
Р9 = 2 • 9! = 2 • 1 • 2 3 • 4 • 5 • 6 • 7 • 8 9 = 725 760.
Ответ: 725 760.
65. Решение задачи 6
• Если 3 указанные книги рассматривать какодну книгу, то 5 книг (7-3 + 1 = 5) можно
расставить Р5 способами. Затем для
каждого полученного способа имеем Р3
способов расстановки 3 книг. По правилу
умножения всего будет Р5 • Р3 вариантов
расстановки книг согласно условию задачи.
Р5 • Р3 = 5! • 3! = 1 • 2 • 3 • 4 • 5 • 1 • 2 • 3 =
720. Ответ: 720.
66. Решение задачи 7
• 7 книг можно расставить на полке Р7способами; Р7 = 1 • 2 • 3 • 4 • 5 • 6 • 7 =
5040. В 720 случаях указанные книги будут
стоять рядом (см. задачу 6). Значит, в
остальных случаях будут выполняться
условия данной задачи. 5040 - 720 = 4320.
Ответ: 4320.
67. Решите задачи
• 8. Сколькими способами можно рассадить 4 учащихся на 20местах?
• 9. Требуется распределить 4 путевки на 4 различные турбазы
среди 9 работников. Каким количеством способов можно это
сделать?
• 10. Сколько трёхзначных чисел можно составить из цифр 9, 8, 7,
6, 2, если цифры в числе не повторяются?
• 11. Ученики 6 класса изучают 11 различных учебных предметов.
Сколькими способами можно составить расписание из 5
различных предметов на понедельник, если математика
должна быть вторым уроком?
• 12. Сколькими способами можно рассадить 6 пассажиров в
разные вагоны (по одному в вагон), если в составе поезда 11
вагонов?
68. Задача 8
Задача 9Задача 10
69. Задача 11
3адача 1270. Задача 13
• Сколько существует пятизначных чисел снеповторяющимися цифрами, которые
делятся на 10?
71. Способы решения задачи 13
72. Задача 14
• Сколько существует двузначных чисел снеповторяющимися цифрами, у которых
обе цифры чётные?
73. Задача 15
• Из 16 рабочих надо выделить 5 длявыполнения некоторой работы. Сколькими
способами это можно сделать?
74. Задача 16
• На плоскости даны 9 точек, никакие 3 изних не лежат на одной прямой. Сколько
прямых можно провести, соединяя точки
попарно?
75. Задача 17
• Сколькими способами можно составитьбукет из 5 цветков, если имеем 8 ромашек
и 7 васильков?
76. Задача 18
• Сколькими способами можно разделитьгруппу из 15 человек на 2 группы так, чтобы
в одной было 10 человек, а в другой — 5?
77. Задача 19
• Сколькими способами читатель библиотекиможет выбрать 3 книги из 5 предложенных
библиотекарем?
78. Задача 20
• В турнире принимали участие 15шахматистов, и каждые 2 шахматиста
встретились один раз. Сколько партий было
сыграно в турнире?
79. Задача 21
• Сколько можно составить из простыхделителей числа 2730 составных чисел,
которые содержат только три простых
делителя?
80. Задача 22
• В коробке лежит 12 синих и 8 красныхкарандашей. Сколькими способами можно
выбрать 3 синих и 2 красных карандаша?
81. Задача 23
• Сколькими способами можно отправить 15школьников в 3 спортивных лагеря, если в
один из них могут принять 8 школьников,
во второй — 3, а в третий — 4 школьника?
82. Решение задачи 23
83. Задача 24
• Сколькими способами можно разделить 10билетов в кино, 4 билета в театр и 3 билета
в цирк среди 17 человек?
84. Решите задачи
• 25. Сколько четырехзначных чисел, кратных10, можно составить из цифр 0,5,7,8, и 9?
• 26. Сколькими различными способами
можно назначить двух ребят на дежурство
в столовой, если в классе 24 учащихся?
• 27. Сколькими различными способами
могут распределиться призовые места
( первое, второе, третье ) между пятью
велогонщиками?
85. Решите задачи
• 28. Сколько различных четырехзначныхчисел можно составить с использованием
нечетных цифр, если цифры в числе не
повторяются?
• 29. Сколько различных трехзначных чисел,
кратных пяти, можно составить из нечетных
цифр, если цифры в числе не могут
повторятся?
86. Решите задачи
• 30. Секретный замок состоит из трехбарабанов, на каждом из которых
набирается одна из цифр от 0 до 9. Сколько
существует способов выбрать код этого
замка, если владелец использует только
нечетные цифры, которые могут
повторятся?
• 31. Сколько существует трехзначных чисел,
в записи которых нет цифры 3?
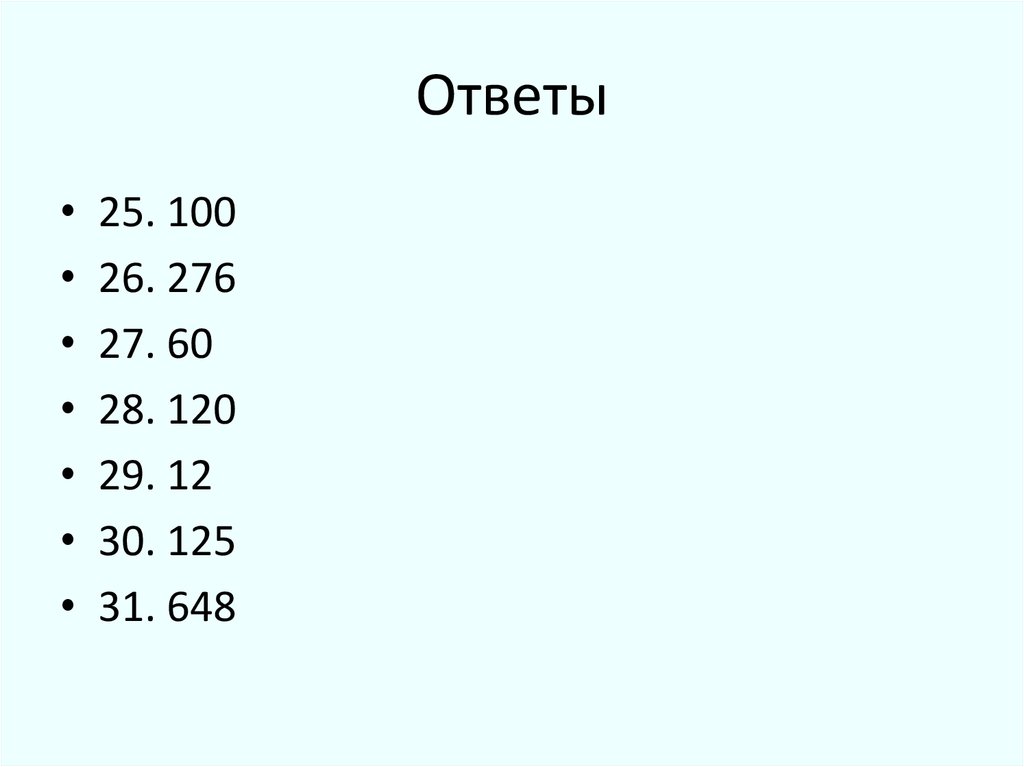
87. Ответы
• 25. 100• 26. 276
• 27. 60
• 28. 120
• 29. 12
• 30. 125
• 31. 648





















































































 Математика
Математика








