Теория вероятностей сложных событий ЕГЭ-2023 (задание №4)

1.

Теория вероятностей
сложных событий
ЕГЭ-2023 (задание №4)
Выполнила Петренко Н.В., учитель
математики МБОУ СОШ №7,
региональный тьютор
ст. Воронежская, Усть-Лабинский район

2.

Задание №3
m то, чтов вопросе
P( A)
n
скольковсего
m
число благоприятных исходов
n
общее число исходов
Что такое исход и чем задание №4 отличается от
задания №3?

3.

Задание №4
Элементарные события (исходы) – простейшие события,
которыми может окончится случайный опыт.
Сумма вероятностей всех исходов случайного опыта всегда
равна 1
Исходы случайного опыта могут быть:
Совместные события – это исходы, которые могут наступить в
одном случайном опыте.
Несовместные события – это исходы, которые не наступают в
одном случайном опыте.
Независимые (зависимые) – это исходы, наступление которых не
зависят (зависят) друг от друга в нескольких случайных опытах.
Противоположные:
называется противоположным событию А, если
состоит из тех и только тех элементарных исходов,
которые не входят в А.
A

4.

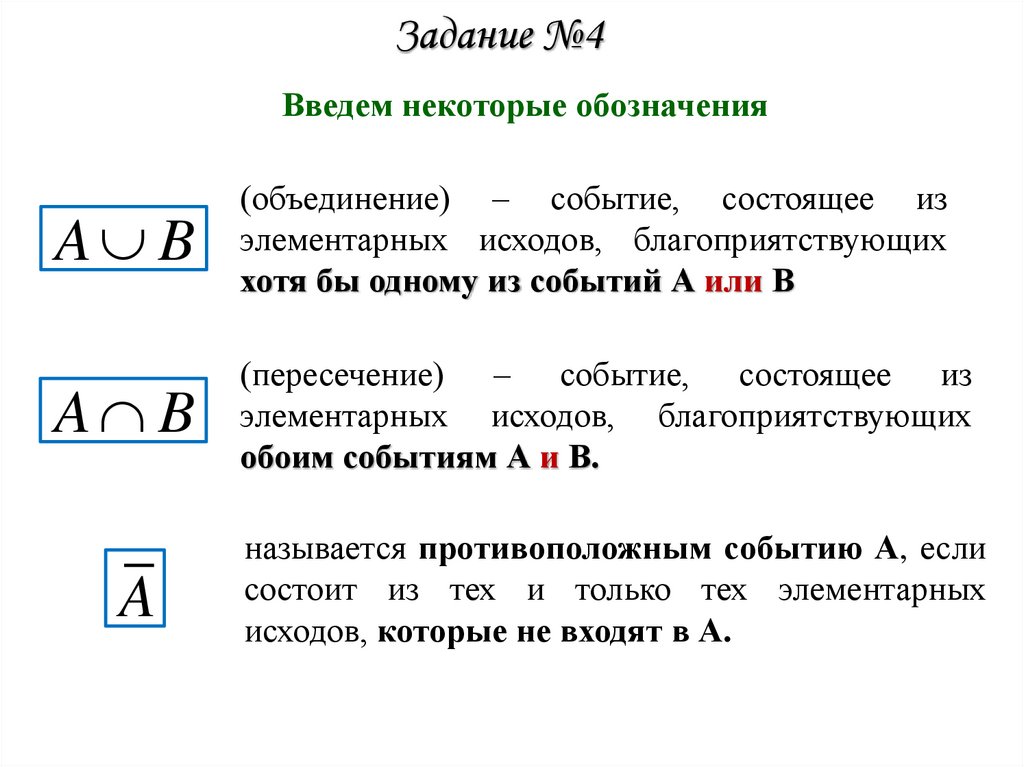
Задание №4
Введем некоторые обозначения
A B
(объединение) – событие, состоящее из
элементарных исходов, благоприятствующих
хотя бы одному из событий А или В
A B
(пересечение) – событие, состоящее из
элементарных исходов, благоприятствующих
обоим событиям А и В.
A
называется противоположным событию А, если
состоит из тех и только тех элементарных
исходов, которые не входят в А.

5.

Задание №4 (дополнительные формулы)
1. Формула сложения для несовместных событий:
Р А В Р А Р В
2. Формула умножения вероятностей независимых событий:
Р А
В Р А Р В
3. Вероятности противоположных событий:
Р А Р А 1
Р А 1 Р А
4. Формула сложения вероятностей совместных:
Р А В Р А Р В Р А В

6.

Пример 1
Игральная кость подбрасывается один раз, какова
вероятность того, что выпадет «2» или «3»?
ИЛИ = «+»
1
P("2")
6
1
P("3")
6
1 1
P("2"или "3")
6 6
1
3

7.

Пример 2
Игральная кость подбрасывается два раза, какова
вероятность того, что выпадет на первой выпадет «2» и
на второй выпадет «3»?
И = «∙»
1
P("2")
6
1
P("3")
6
1 1
P("2"и "3")
6 6
1
36

8.

Пример 3
Игральная кость подбрасывается 3 раза, какова вероятность
того, что 6 появится хотя бы раз?
Исходы, которые влияют на решение задачи:
666 66Н 6Н6 Н66 НН6 Н6Н 6НН ННН
Благоприятные события
5 5 5
P ( A)
6 6 6
Противоположное
событие
5 5 5
P( A) 1 P( A) 1
6 6 6
91
216

9.

1
Вероятности сложных событий
Демо-версия ЕГЭ-2022
Симметричную игральную кость бросили 3 раза.
Известно, что в сумме выпало 6 очков. Какова
вероятность события «хотя бы раз выпало 3
очка»?
123 141
132 114
213 411
231
312
222
n=10
m=6
6