Многогранники

1.

Многогранники

2.

Александрийский маяк
В 285 г. до н.э. на острове
Фарос архитектор Сострат
Книдский построил маяк в
виде трехэтажной башни.
Восьмигранник
Параллелепипед

3.

Египетские пирамиды
Египетские пирамиды словно
вырастают из песков
пустыни колоссальные,
величественные,
подавляющие
человека
необычайными
размерами и
строгостью очертаний. Стоя у
подножия пирамиды, трудно себе
представить, что эти огромные
каменные горы созданы руками
людей. А между тем они были
действительно
сложены
из
отдельных каменных глыб, как в
наше время дети складывают
пирамиды из кубиков.

4.

Москва - СИТИ
здания в форме параллелепипеда.

5.

Спасская башня Казанского Кремля
Четыре яруса башни
представляют собой
пирамида
многогранники
куб

6.

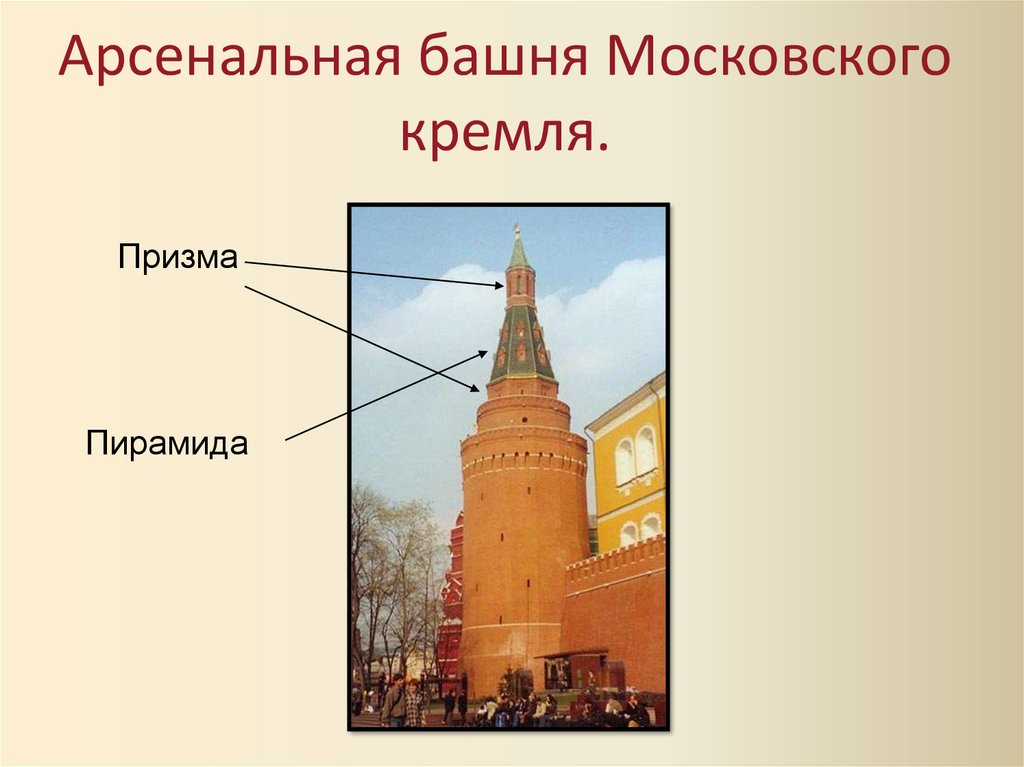
Арсенальная башня Московского
кремля.
Призма
Пирамида

7.

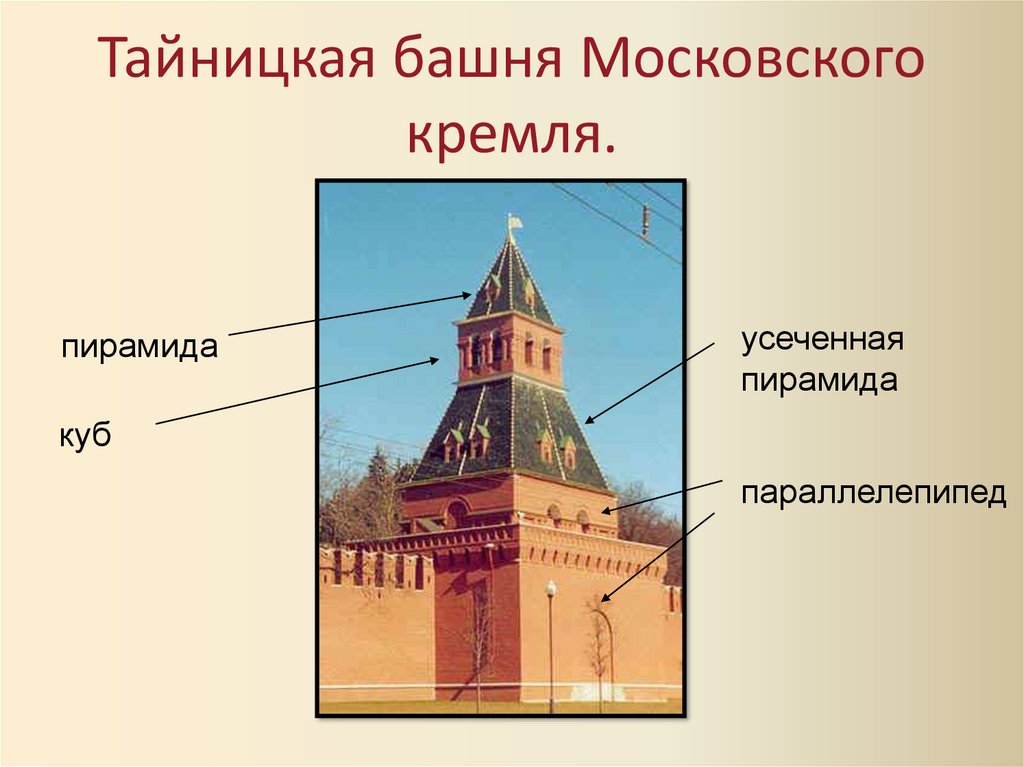
Тайницкая башня Московского
кремля.
пирамида
усеченная
пирамида
куб
параллелепипед

8.

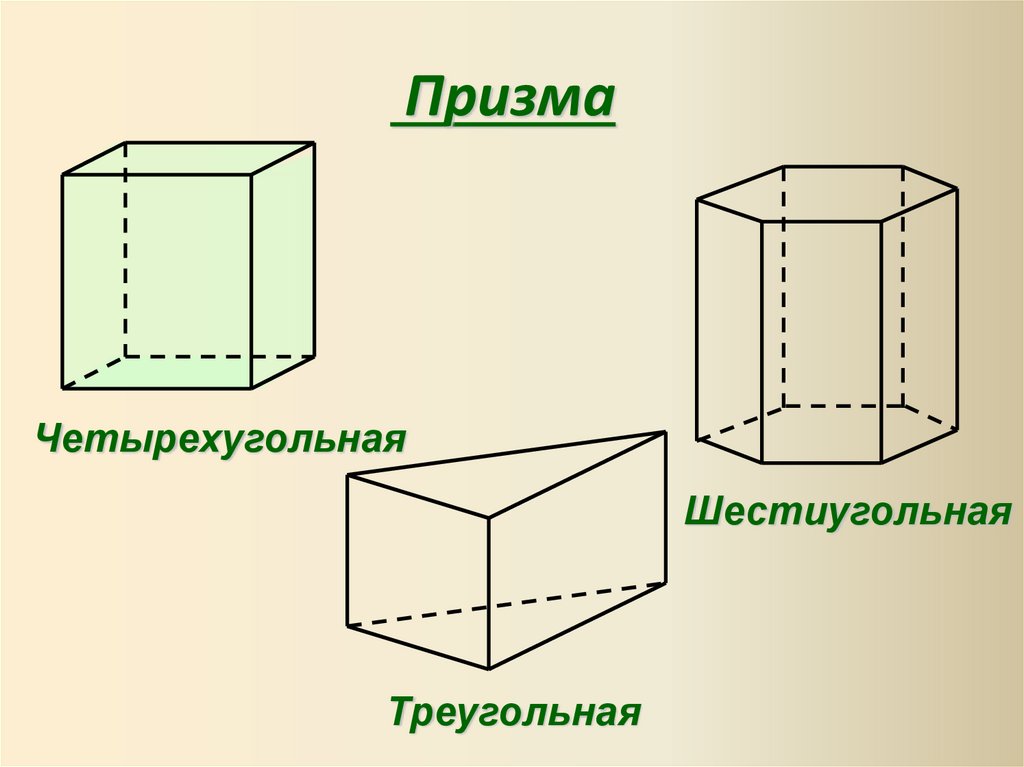
Призма
Четырехугольная
Шестиугольная
Треугольная

9.

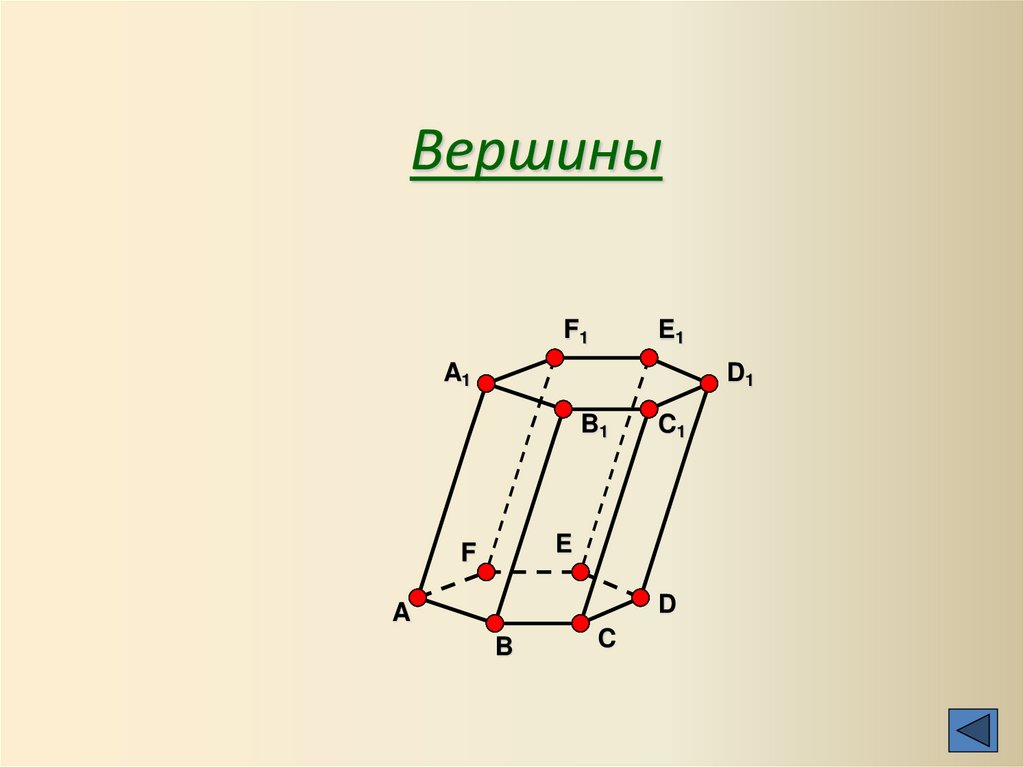
Вершины
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

10.

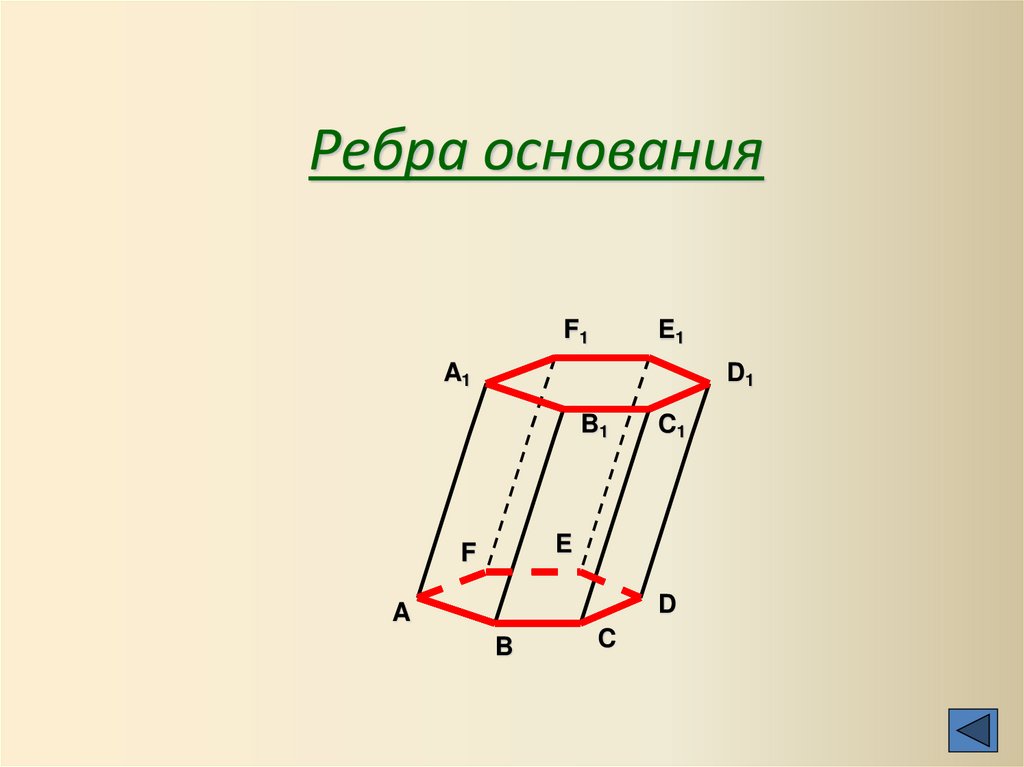
Ребра основания
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

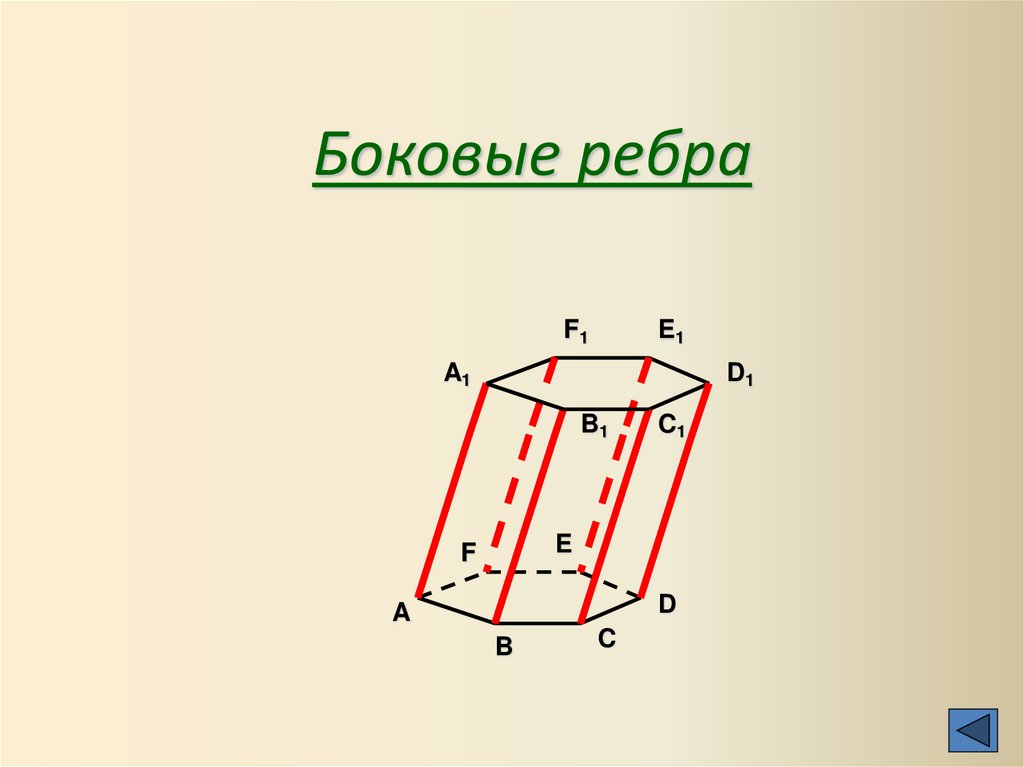
11.

Боковые ребра
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

12.

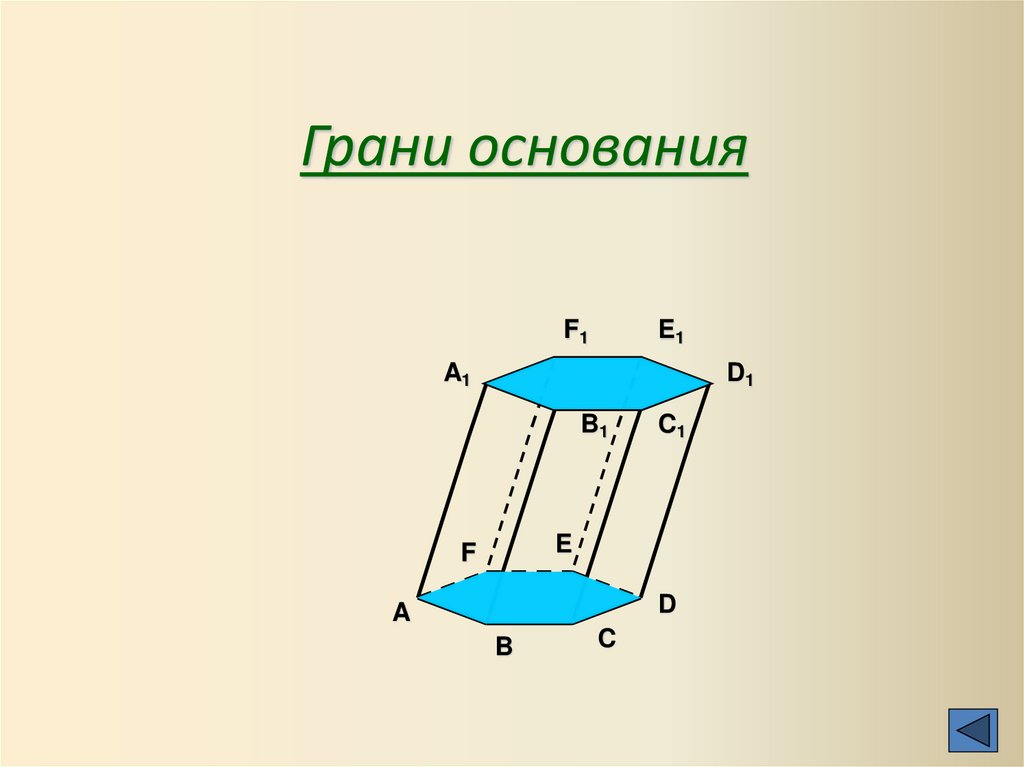
Грани основания
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

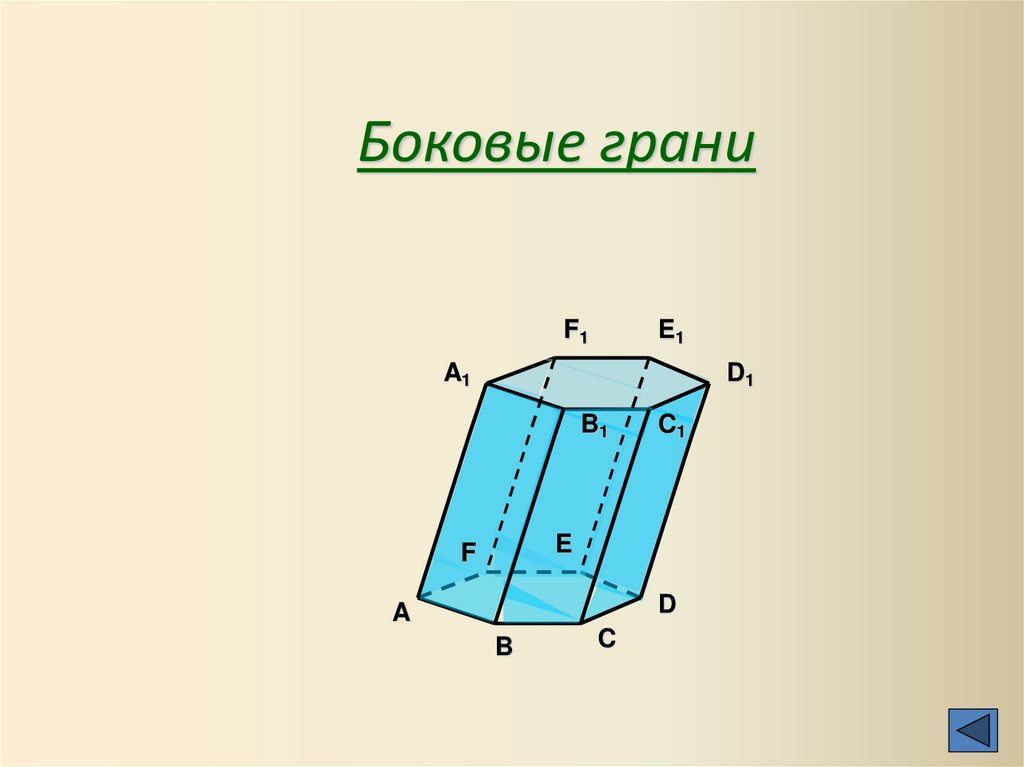
13.

Боковые грани
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

14.

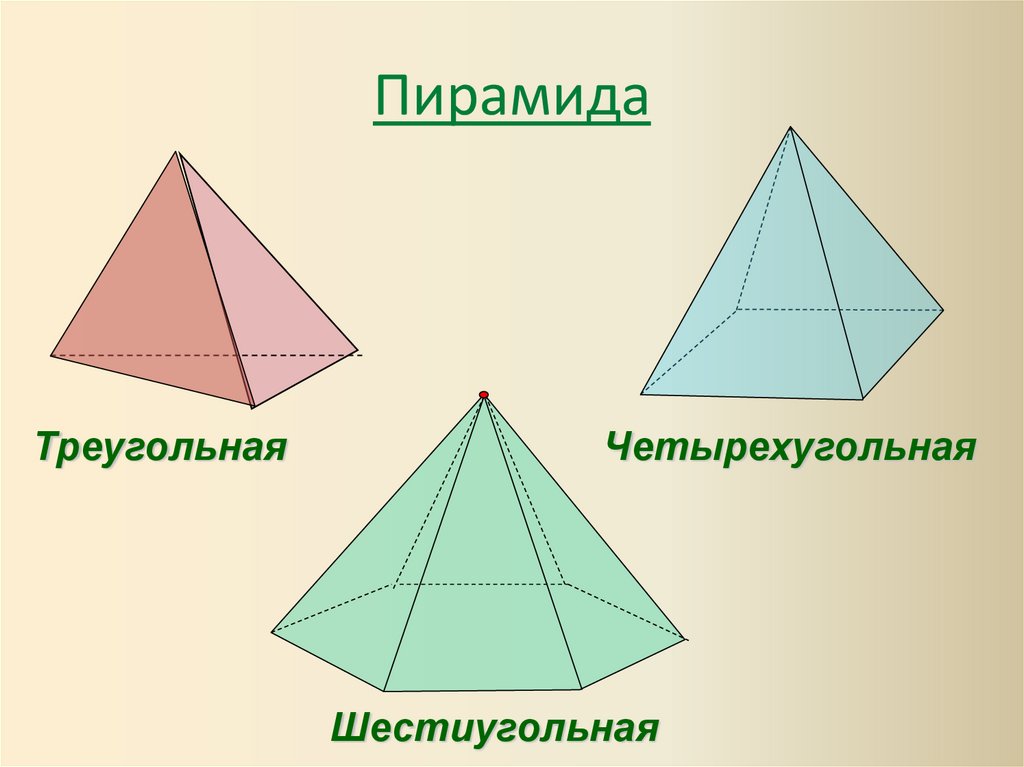
Пирамида
Треугольная
Четырехугольная
Шестиугольная

15.

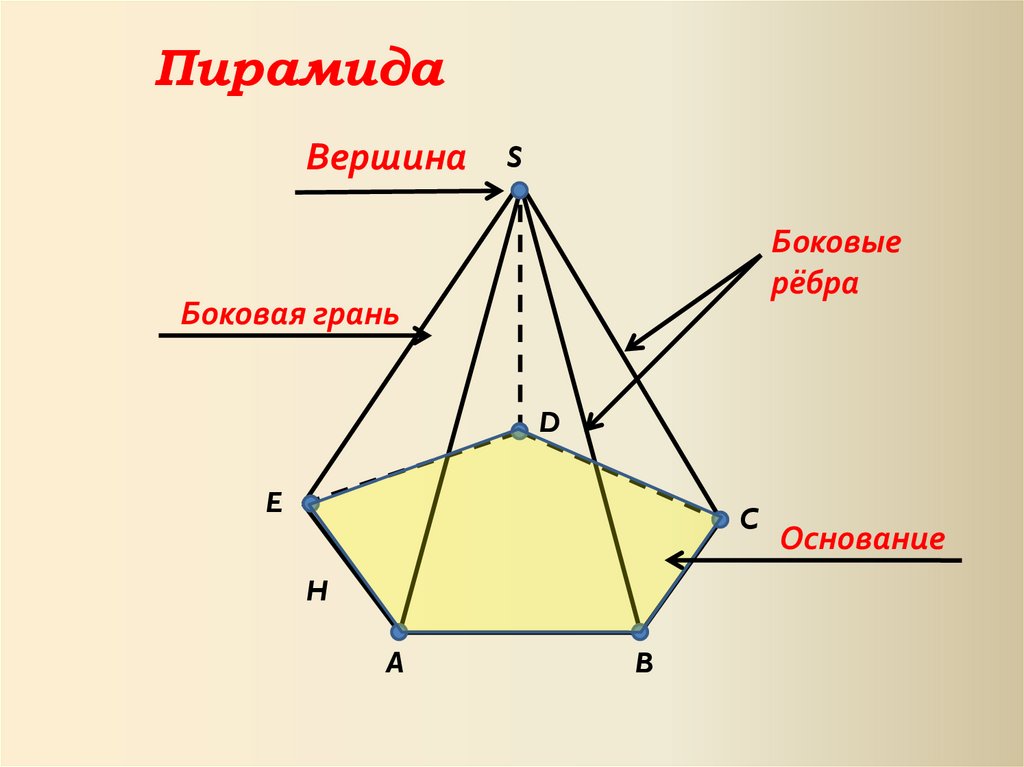
Пирамида
Вершина
S
Боковые
рёбра
Боковая грань
D
E
C
H
A
B
Основание

16.

S
N
K
M
L
B
C
B
A
A
C
D
D
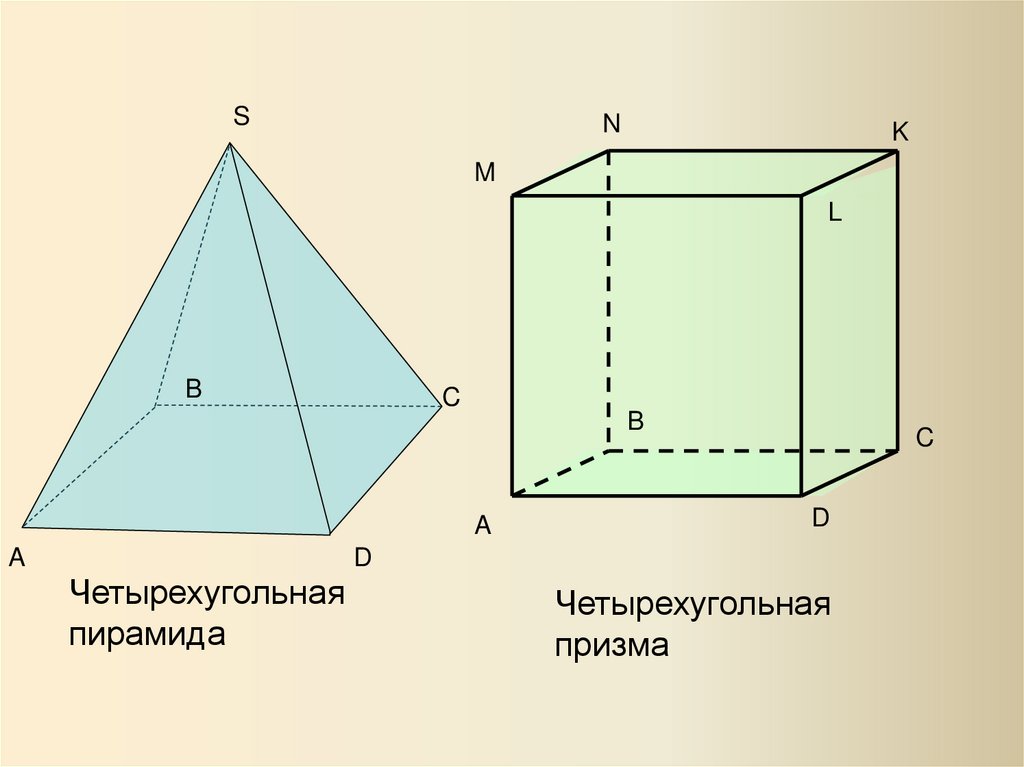
Четырехугольная
пирамида
Четырехугольная
призма

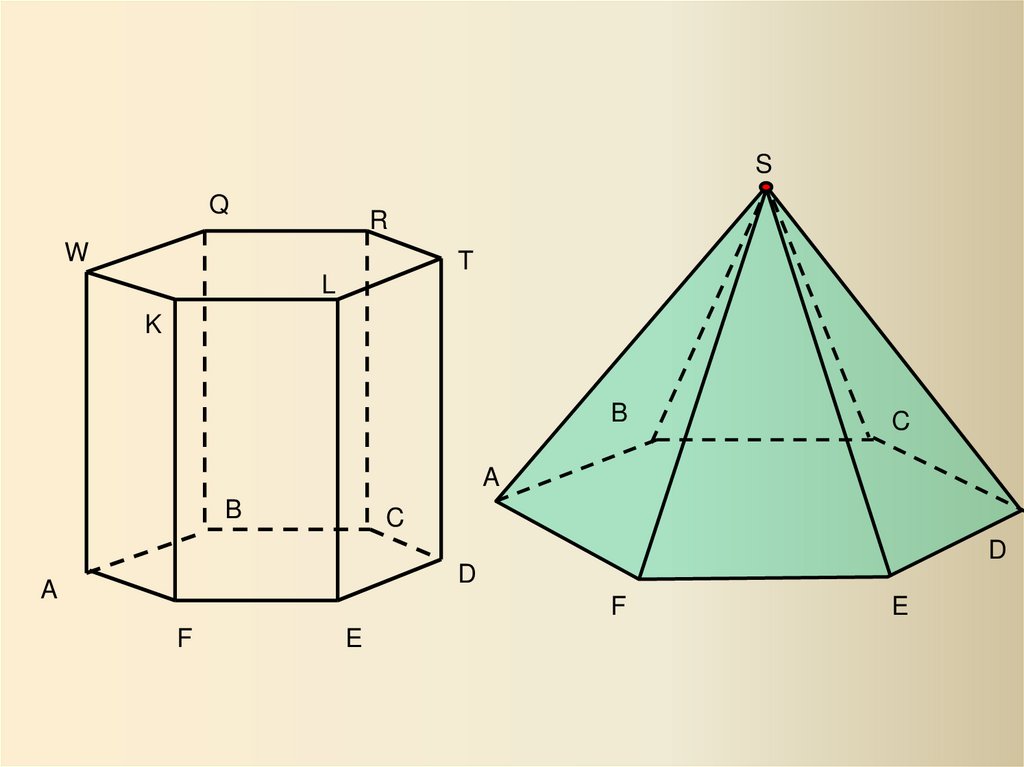
17.

S
Q
R
W
T
L
K
B
C
A
B
C
D
D
A
F
F
E
E

18.

Отдохнем!!!

19.

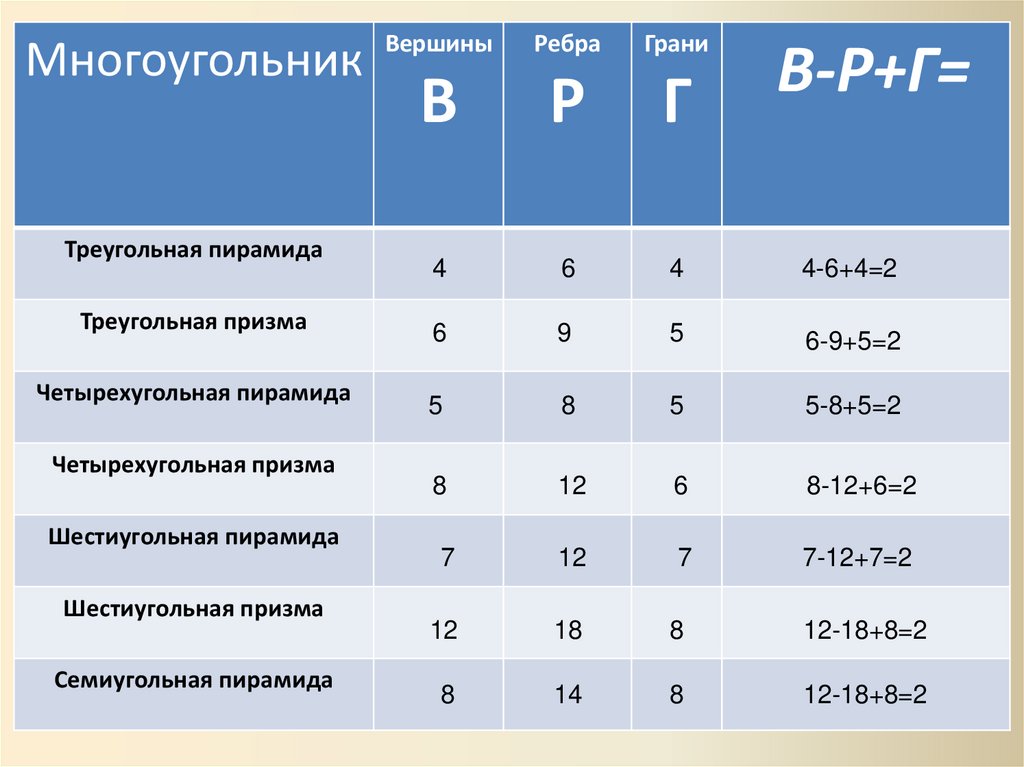
Вершины
Ребра
Грани
В
Р
Г
4
6
4
4-6+4=2
Треугольная призма
6
9
5
6-9+5=2
Четырехугольная пирамида
5
8
5
5-8+5=2
8
12
6
8-12+6=2
7
12
7
7-12+7=2
12
18
8
12-18+8=2
8
14
8
12-18+8=2
Многоугольник
Треугольная пирамида
Четырехугольная призма
Шестиугольная пирамида
Шестиугольная призма
Семиугольная пирамида
В-Р+Г=

20.

ЛЕОНАРД ЭЙЛЕР
(1707-1783)
Математик, механик,
физик и астроном.
По происхождению швейцарец. В
1726 был приглашен в
Петербургскую академию наук
и переехал в 1727
в Россию.

21.

22.

Огонь
Воздух
Вода
Земля
Все мироздание

23.

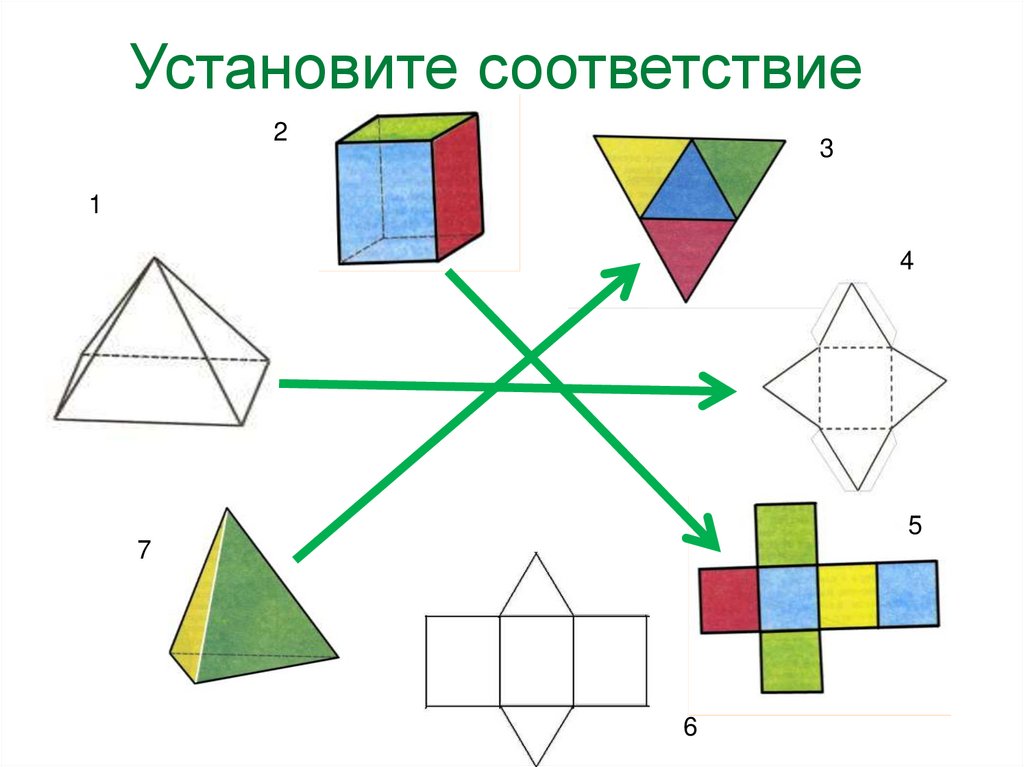
Установите соответствие
2
3
1
4
5
7
6

24.

25.

Домашнее задание:
1. № 771
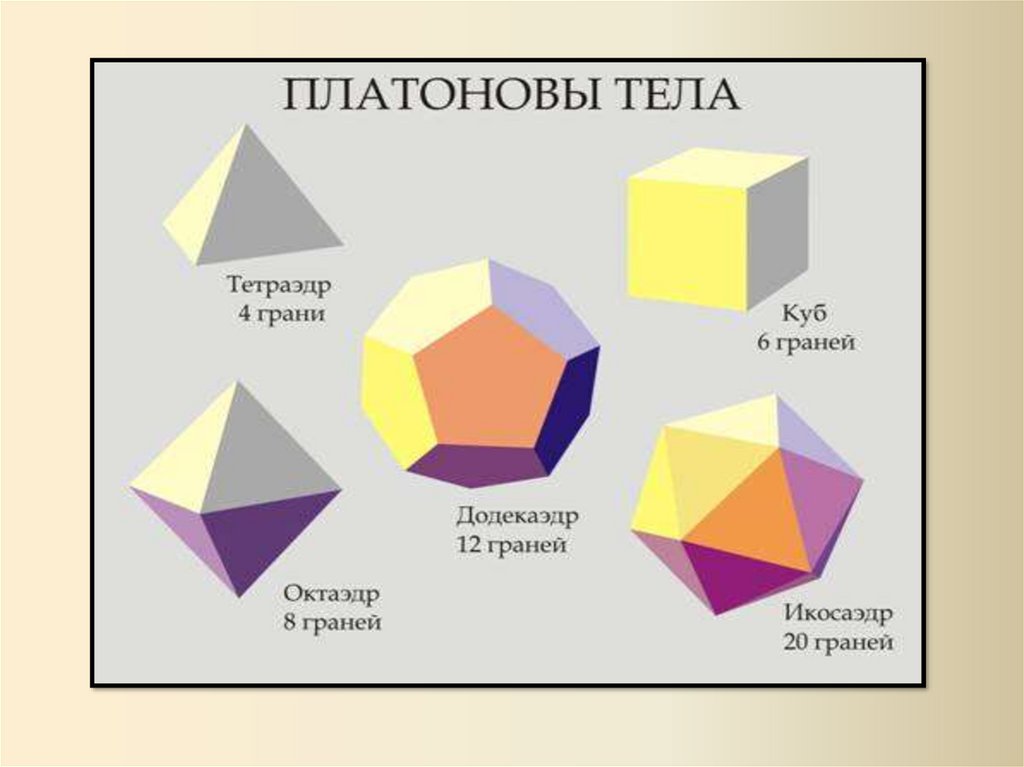
2. Изучить самостоятельно
Платоновы тела,
проверить, справедлива
ли для них формула
Эйлера.