Прямолинейное равномерное движение

1. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ

2.

ПРОВЕРЬ СЕБЯ
1. Дайте понятие системы отсчета
2. Сколькими координатами задается
положение тела :
а) на прямой
б) на плоскости
в) в пространстве
3. Дайте определение перемещения
4. В каком случае путь и перемещение
совпадают
( при прямолинейном движении в
одном направлении)
5. Может ли путь быть ненулевым при
нулевом перемещении ?
( да, если начальное и конечное
положение тела совпадают)
у
0
S
у
у0
х0
х
S
х
S -путь
z
S-перемещение
у
х
х0
уS0
S
S= 2 Пr
S =z00
х0
х

3.

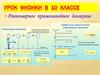
ПРОВЕРЬ СЕБЯ
6. В каком случае проекция вектора на ось считается
- положительной
- отрицательной
- равной нулю
• Если от проекции начала вектора к проекции
его конца надо двигаться по направлению оси
• Если от проекции начала вектора к проекции
его конца надо двигаться в направлении,
противоположном направлению оси
• Если вектор перпендикулярен оси координат
7. Изобразите векторы, проекции которых
удовлетворяют следующим условиям :
aх> 0
в х< 0
Сх = 0
aу> 0
ву = 0
Су < 0
с
в
а
х
aх> 0
сх= 0 вх< 0

4.

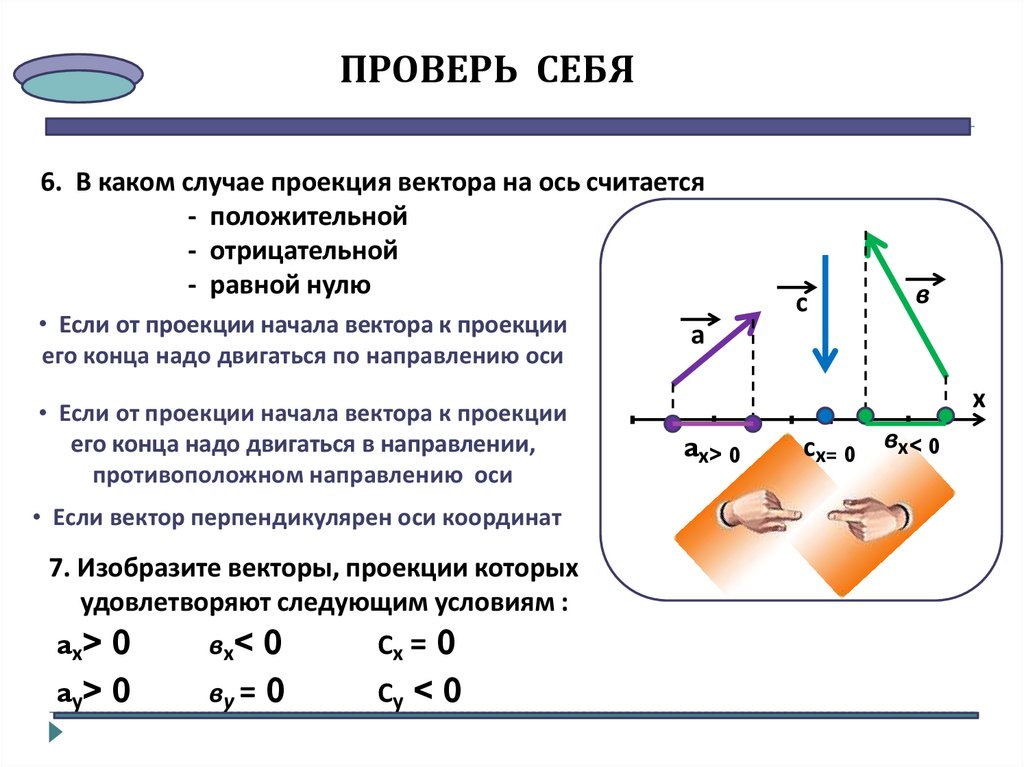
ПРОВЕРЬ СЕБЯ
8. Вспомните, как связаны проекция вектора перемещения
и координаты тела
Sx = х - х0
Sy = y - y0
9. Вспомним формулы для расчета
координат тела в любой
момент времени
х = х0 + sx
y = y0 + sy
Данные формулы могут принимать разный
вид в зависимости от того, как движется тело.
Сегодня мы узнаем, как будут
выглядеть ЭТИ формулы
для равномерного прямолинейного движения
у
у
Sу
S
у0
Sх
х0
х
х

5.

Движение называется равномерным, если за любые равные
промежутки времени тело проходит одинаковые пути
Может быть криволинейным
Может быть прямолинейным
(траектория – кривая линия)
( траектория – прямая линия)
1с
1с
1с
1с
1с
1с
1с
1с
1с
1с
Равномерное прямолинейное движение –
самый простой вид движения:
• траектория – прямая линия
• за любые равные промежутки времени
тело проходит равные пути

6.

Одинаковым
ли будет для
данных случаев
Рассмотрим равномерное
прямолинейное
движение тела
двух одинаковых
перемещение
в единицутел
времени?
t1= t2
S1
0
S2
х1
х2
Чем отличаются данные движения?
Чем сходны данные движения?
S1= S2
t1 < t2
S1
0
S2
S1< S2
х1 = х 2
х
х

7.

Очевидно, что перемещение, совершаемое телами в единицу времени,
в рассмотренных примерах различно, т.е. тела имеют разную скорость.
Скоростью равномерного прямолинейного движения называют векторную
величину, равную отношению перемещения тела к промежутку времени,
в течение которого это перемещение произошло
v
s
v=
t
0
х
х0
S
х
v – векторная величина, направленная так же, как и перемещение
Выясним физический смысл модуля скорости:
s
х - х0
v=
=
t
t
Скорость показывает , какое расстояние пройдено телом в единицу времени,
т.е. быстроту изменения координаты тела

8.

Каков смысл данных значений скоростей тел ?
v= 10 м/с
v= 25 м/мин
Это значит, что за каждую секунду тело проходит 10 м
v= 300 км/ч
v= 7,9 км/с
За каждый час тело проходит путь, равный 300 км
За каждую минуту координата тела изменяется на 25м
За каждую секунду тело проходит путь, равный 7,9 км
Важно помнить, что единицей скорости в СИ является 1 м/с
Способы перевода в СИ:
1. 36 км/ч - 10 м/с
108 км/ч – х м/с
Х = 1о8 х 10/ 36 = 30 м/с
2. 300 м/мин = 300 м/60 с = 5 м/с
162 км/ч = 162 000 м / 3 600 с = 45 м/с

9.

Работаем с проекциями величин
Проекция скорости vx и перемещения sx
Положительна
если тело движется в
положительном направлении
оси координат ( х > х0 )
vx2 > 0
Sx2 > 0
Отрицательна
если тело движется в
отрицательном направлении
оси координат ( х < х0 )
vx3 = 0, Sx3 = 0
v1
0
х02
х2
S2
vx1 = 0, Sx1= 0
v4
v3=0
v2
х1
vx4 < 0
Sx4 < 0
Равна нулю, если тело покоится
или движется в направлении,
перпендикулярном оси координат ( х = х0 )
х03
х4
х04
S4
х

10.

Если известна начальная координата
и скорость движения, можно определить координату тела
в данный момент времени
х - х0
vx =
t
х - х0 = vx t
х= х0 + vx t
Полученная формула может видоизменяться в зависимости
от знака проекции скорости и значения начальной координаты
v2
v1
х2 0
х= х1 + v1 t
т.к. v1x > 0
х1
v3
х3
х = - v2 t
х= х3 – v3 t
т.к. v3x < 0
х
т.к. v2x < 0 , x2= 0

11.

Графическое представление движения
Графики скорости ( модуля скорости)
и проекции скорости
v,м/с
vx,м/с
v1x>0
40
70
v1
60
50
0
v2
-10
S2
10
-20
t,с
1
2
3
4
t,с
10
30
20
S1x
20
S1
40
0
30
5
6
7
8
Позволяет сравнить численные значения
скоростей, но направления движения
определить не позволяет
-30
1
2
3
4
S2x
5
6
7
v2x< 0
-40
Позволяет сравнить численные значения
скоростей и определить направление
движения тел.

12.

График зависимости координаты от времени
х= х0 +vx t
Учимся «читать» графики
х, м
50
х - х0
vx 1 = х - х 0
vx 2 =
t
t
3
40
1
Тело движется из точки с координатой
в положительном
х0 = - 20 м
Тело движется
из точки
с координатой
направлении
ОХ ( т.к. vx1> 0 )
в отрицательном
х0 = 50 м оси
0)
равномерно
соОХ
скоростью
направлении
оси
( т.к. vx25<м/с
равномерно
со скоростью
10 вид:
м/с
x(t) имеет
Зависимость
t,с
х = -20
5t вид:
x(t)+ имеет
Зависимость
30
20
10
0
1
2
3
4 5
t=4c
t=5c
0 м – (-20 м)
=0 м – 50 м
= 5 м/с
=
4c
= -10 м/с
5c
1 тело х0 = - 20 м х = 0 м
х= 0 м
2 тело х0 = 50 м
х = 50 - 10t
6
-10
-20
2
-20
0
0
x
50
-30
3 тело - самостоятельно
х