Neurčitý integrál primitívna funkcia

1. 1. NEURČITÝ INTEGRÁL PRIMITÍVNA FUNKCIA

DEFINÍCIA Funkcia F sa nazýva primitívna funkcia k funkcii f
na intervale J , ak pre všetky x J je F x f x (v krajných
bodoch intervalu uvažujeme jednostranné derivácie).
VETA Nech funkcia F je primitívna funkcia k funkcii f na intervale
J a C R , potom aj funkcia G F C je primitívnou funkciou k
funkcii f na intervale J.
Poznámka Ak teda k danej funkcii f existuje primitívna funkcia F na
intervale J, existuje ich nekonečne veľa.

2. 1. NEURČITÝ INTEGRÁL PRIMITÍVNA FUNKCIA

DEFINÍCIA Množinu F C; C R všetkých primitívnych funkcií k
funkcii f, označujeme symbolom
f x dx
nazývame
neurčitý
integrál. Píšeme f x dx F x C .
Poznámka Platí
f x .
f
x
dx
f
x
C
,
f
x
dx
Proces hľadania primitívnej funkcie k danej funkcii nazývame
integrovaním alebo
integráciou funkcie, argument x nazývame
integračnou premennou, konštantu C
konštantou.
nazývame integračnou

3. 1. NEURČITÝ INTEGRÁL VÝPOČET PRIMITÍVNEJ FUNKCIE

VETA Nech funkcia f je spojitá na intervale J, potom k nej na
intervale J existuje primitívna funkcia F .
VETA (Veta o lineárnosti) Nech k funkciám f a g existujú primitívne
funkcie na intervale J a aspoň jedna z reálnych konštánt a, b je rôzna
od nuly. Potom existuje primitívna funkcia k funkcii af bg na
intervale J a platí
a f x b g x dx a f x dx b g x dx .

4. 1. NEURČITÝ INTEGRÁL NIEKTORÉ ZÁKLADNÉ VZORCE INTEGROVANIA

Vzorce platia na intervaloch, na ktorých sú funkcie definované.
a dx a x C
x a 1
x dx a 1 C
a
pre a R ,
pre a 1 ,
x
x
C,
e
dx
e
cos x dx sin x C ,
1
a2 x
1
x dx ln x C ,
ax
x
a dx ln a C
sin x dx cos x C ,
pre a 0, a 1 ,
dx
2
dx
x2 a2
a x
1
C,
ln
2a a x
ln x x 2 a 2 C ,
f x
f x dx ln f x C .

5. 1. NEURČITÝ INTEGRÁL SUBSTITUČNÁ METÓDA

VETA Nech : a, b , má spojitú deriváciu. Nech F je
primitívna funkcia k funkcii f t na , . Potom funkcia F x
je primitívna k f x x na a, b .
Túto vetu je možné prepísať pomocou integrálov, čo nás privedie
k substitučnej metóde.
x t
f x x dx x dx dt f t dt .

6. 1. NEURČITÝ INTEGRÁL METÓDA PER PARTES

VETA Nech funkcie u x , v x majú spojité derivácie na intervale J.
Potom na intervale J platí u x v x dx u x v x u x v x dx .

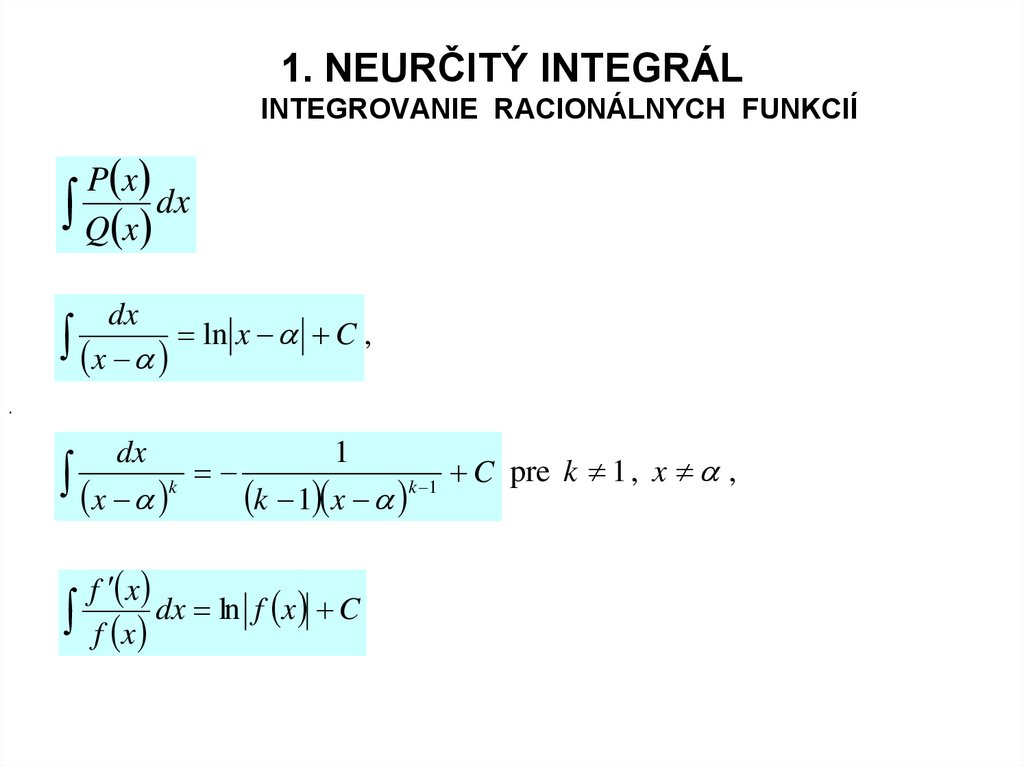
7. 1. NEURČITÝ INTEGRÁL INTEGROVANIE RACIONÁLNYCH FUNKCIÍ

P x
Q x dx
dx
x ln x C ,
.
dx
x
k
1
k 1 x
f x
f x dx ln f x C
k 1
C pre k 1 , x ,

8. 1. NEURČITÝ INTEGRÁL INTEGROVANIE IRACIONÁLNYCH FUNKCIÍ Lineárna iracionalita

Integrál typu R[ x, 1 Ax B , 2 Ax B , , n Ax B ] dx , kde R je
k
k
k
racionálna funkcia a k1 , k 2 , , k n sú prirodzené čísla, riešime
pomocou substitúcie
Ax B t k ,
pričom k je najmenší spoločný násobok čísel k1 , k 2 , , k n . Pomocou
tejto substitúcie prevedieme daný integrál na integrál z racionálnej
funkcie.

9. 1. NEURČITÝ INTEGRÁL INTEGROVANIE IRACIONÁLNYCH FUNKCIÍ Kvadratická iracionalita

Integrál typu
dx
Ax 2 Bx C
, kde A 0 ,
riešime úpravou výrazu pod odmocninou na štvorec a následnou
substitúciou nájdeme riešenie tohto integrálu pomocou integračného
vzorca
dx
x2 a2
ln x x 2 a 2 C .

10. 1. NEURČITÝ INTEGRÁL INTEGROVANIE IRACIONÁLNYCH FUNKCIÍ Kvadratická iracionalita

Integrál typu
Pn x
Ax 2 Bx C
dx , A 0 , počítame pomocou tzv.
Ostrogradského metódy (metódy neurčitých koeficientov), pričom
vytvoríme nasledujúcu rovnosť, kde Pn x je polynóm n-tého stupňa,
Qn 1 x je polynóm stupňa n 1 a k je neznáma konštanta
Pn x
Ax 2 Bx C
dx Qn 1 x Ax 2 Bx C k
dx
Ax 2 Bx C
.

11. 1. NEURČITÝ INTEGRÁL INTEGROVANIE EXPONENCIÁLNYCH FUNKCIÍ

x
x
vypočítame
pomocou
substitúcie
R
(
e
)
dx
e
t.

12. 1. NEURČITÝ INTEGRÁL INTEGROVANIE GONIOMETRICKÝCH FUNKCIÍ

R(sin x) cos x dx vypočítame pomocou substitúcie sin x t .
R(cos x) sin x dx vypočítame pomocou substitúcie cos x t .