Number System

1. Number System

A number system is defined as a system of writing to express numbers.
It is the mathematical notation for representing numbers of a given set by using
digits or other symbols in a consistent manner.
Humans use the DECIMAL system (“deci” stands for “ten”)
To convert data into strings of numbers, computers use the BINARY number system
Elementary storage units inside computers are electronic switches.
Each switch holds one of two states: on (1) or off (0).
ON
OFF
We use a bit (binary digit), 0 or 1, to represent the state.
0 (00)
1 (01)
2 (10)
3 (11)

2.

Bits and Bytes
A bit is the smallest unit of information a computer can use, having a value of 1 or 0.
Computers work with collections of bits, grouping them to represent larger pieces of data,
such as letters of the alphabet.
Eight bits make up one byte. A byte is the amount of memory needed to store one
alphanumeric character.
With one byte, the computer can represent one of 256 different symbols or characters.
1 01
10
1 01
01 1 01

3. Common Number Systems

System
Base
Symbols
Decimal
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binary
2
0, 1
Octal
8
0, 1, 2, 3, 4, 5, 6, 7, 10, ….
Hexadecimal
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
A, B, C, D, E, F, 10, …

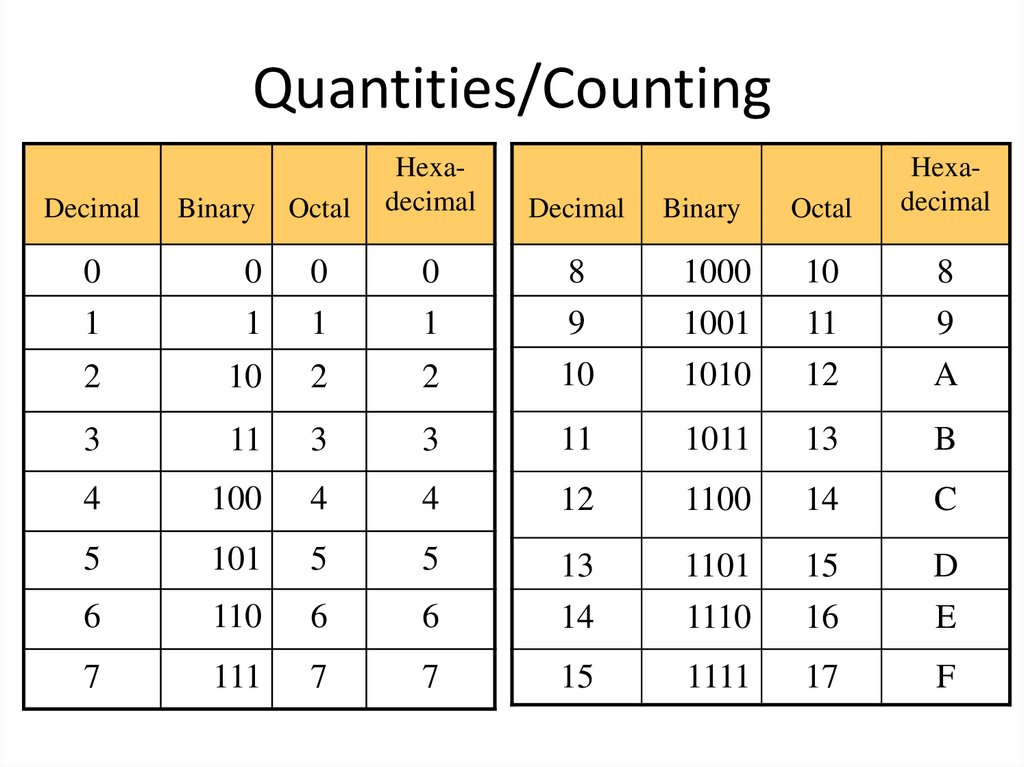
4. Quantities/Counting

Decimal
Binary
Octal
Hexadecimal
Decimal
Binary
Octal
Hexadecimal
1000
1001
1010
10
11
12
8
9
A
0
1
0
1
0
1
0
1
2
10
2
2
8
9
10
3
11
3
3
11
1011
13
B
4
100
4
4
12
1100
14
C
5
101
5
5
6
110
6
6
13
14
1101
1110
15
16
D
E
7
111
7
7
15
1111
17
F

5. Decimal to Binary

Repeated Division-by-2 Method (for whole number)
To convert a whole number to binary, use successive division by 2 until the quotient
is 0. The remainders form the answer, with the first remainder as the least
significant bit (LSB) and the last as the most significant bit (MSB).
(43)10 = (101011)2

6. Example

12510 = ?2
2 125
2 62
2 31
2 15
7
2
3
2
1
1
0
1
1
1
1
12510 = 11111012

7. Binary to Decimal

• Technique
– Multiply each bit by 2n, where n is the “weight” of
the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results

8. Example

Bit “0”
1010112 =>
1 x 20 =
1 x 21 =
0 x 22 =
1 x 23 =
0 x 24 =
1 x 25 =
1
2
0
8
0
32
4310

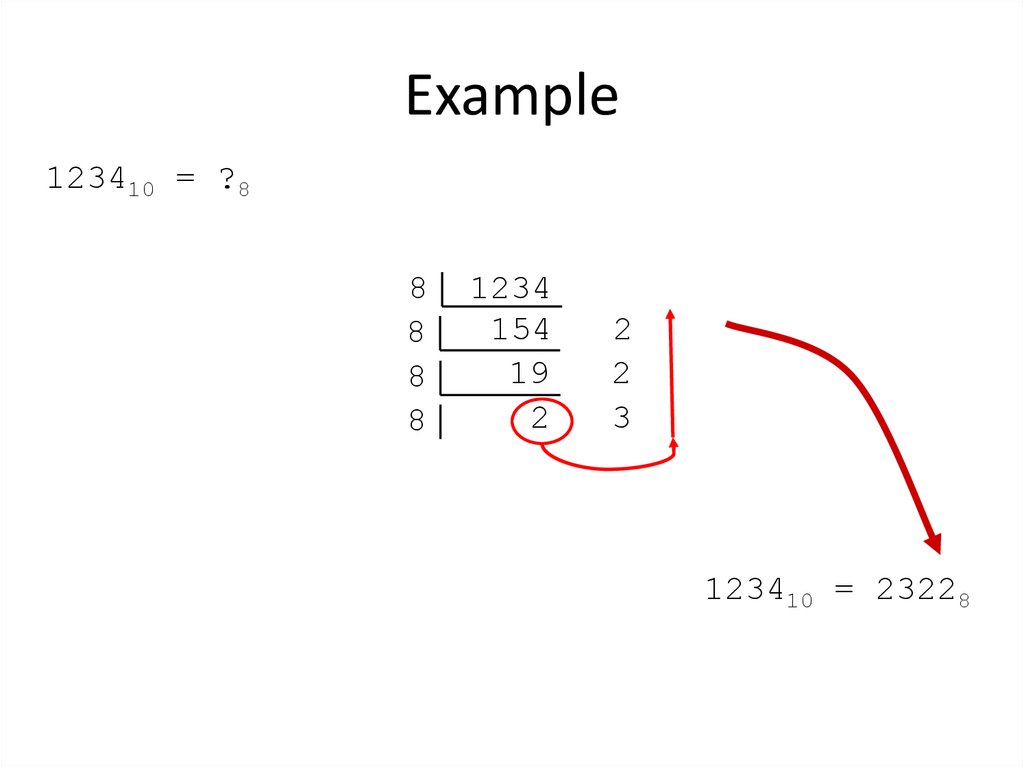
9. Decimal to Octal

• Technique
– Divide by 8
– Keep track of the remainder

10. Example

123410 = ?8
8
8
8
8
1234
154
19
2
2
2
3
123410 = 23228

11. Octal to Decimal

• Technique
– Multiply each bit by 8n, where n is the “weight” of
the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results

12. Example

7248 =>
4 x 80 =
2 x 81 =
7 x 82 =
4
16
448
46810

13. Decimal to Hexadecimal

• Technique
– Divide by 16
– Keep track of the remainder

14. Example

123410 = ?16
16
16
16
1234
77
4
2
13 = D
123410 = 4D216

15. Hexadecimal to Decimal

• Technique
– Multiply each bit by 16n, where n is the “weight”
of the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results

16. Example

ABC16 =>
C x 160 = 12 x
1 =
12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810

17. Exercise – Convert ...

Decimal
33
Binary
Octal
Hexadecimal
1110101
703
1AF
Don’t use a calculator!
Skip answer
Answer

18. Exercise – Convert …

Answer
Hexadecimal
Decimal
33
Binary
100001
Octal
41
117
1110101
165
75
451
111000011
703
1C3
431
110101111
657
1AF
21

19. Thank you