Дискретная математика. Теория множеств

1.

Дискретная математика
Презентации к курсу лекций
Преподаватель: Шамшев Анатолий
Борисович
Блог: http://anshamshev.wordpress.com

2.

Литература
– Новиков Ф. А. Дискретная математика для программистов :
учеб. пособие для вузов / Ф. А. Новиков. - 2-e изд. - СПб. [и
др.] : Питер, 2005
– Шевелев, Ю. П. Дискретная математика : учеб. пособие
для вузов / Ю. П. Шевелев. - СПб. [и др.] : Лань, 2008.
– Хаггарти, Род. Дискретная математика для программистов
: учеб. пособие для вузов / Род Хаггарти ; пер. с англ. под
ред. С. А. Кулешова с доп. А. А. Ковалева, В. А.
Головешкина, М. В. Ульянова . - 2-e изд., доп. - М. :
Техносфера, 2005
– Плотников, А. Д. Дискретная математика : учеб. пособие /
А. Д. Плотников. - М. : Новое знание, 2005
– Судоплатов, С. В. Дискретная математика : учебник для
вузов / С. В. Судоплатов, Е. В. Овчинникова ; М-во
образования и науки Рос. Федерации, Новосибир. гос. техн.
ун-т. - 2-е изд., перераб. - М. ; Новосибирск : Инфра-М :
НГТУ, 2005.
2

3.

Структура курса
1. 8 лекционных занятий
2. 16 практических занятий
3. Расчётно-графическая работа
4. Экзамен
3

4.

Балльно-рейтинговая система
• Виды работ, способы контроля и оценки:
– Лекции – 8 лекций – опросы – 2 балла (2 – «+», 1 – «+/-»). Всего 16
баллов
– Контрольные – 4 контрольные – 5 баллов. Всего 20 баллов
– РГР – 3 задачи по 4 балла (3 балла - задача, 1 - доп. вопрос по
теме задачи), дополнительный теоретический вопрос (по всему
курсу) - 3 балла. Всего 15 баллов. Для сдачи РГР необходимо
набрать 12 баллов.
– Максимальное количество баллов – 51 балл
– Сроки сдачи: лекции – даты лекционных занятий, контрольные –
даты написания, РГР – последнее занятие семестра. Если работа
сдана позже срока, оценка снижается на 20%.
• Критерии допуска:
– Экзамен – сдача всех контрольных работ со средним баллом не
менее 3.0 и сданная РГР.
• Текущие достижения – файлы в папке «Оценки групп»
• Оценки экзамена (дробные оценки округляются по правилам
округления) (автомат по предмету):
– 46 - 51 балл – оценка «5»
– 36 – 45 баллов – оценка «4»
– 25 – 35 баллов – оценка «3».
4

5.

Для чего нужна и области
применения дискретной математики
• Формальное представление задачи
• Доказательство корректности алгоритмов
• Готовые алгоритмы с доказанной
корректностью, сведение задач
• Область применения: любая предметная
область, в которой можно выделить
отдельные объекты и их взаимосвязи
5

6.

Теория множеств
• Множества
• Операции над множествами
• Упорядоченные множества
• Соответствия
• Отображения и функции
• Отношения
6

7.

Множество. Основные понятия
• Множество – некоторая неупорядоченная
совокупность однородных различимых
объектов или элементов.
• Элемент множества отдельный объект множества.
• Конечные множества можно задавать
перечислением их элементов. При
перечислении элементов множества
можно использовать характеристически
свойства.
7

8.

Способы задания множеств
• Перечисление элементов
М = {a1, a2, a3, …, ak}
M9 = {1, 2, 3, 4, 5, 6, 7, 8, 9}
• Выделение определяющего свойства
M = {x | P(x)}
M9 = {n | n & n < 10}
• Определение порождающей процедуры
M = {x | x = f}
M9 = {n | for n from 1 to 9 write n}
Иные способы, определяемые потребностями
решаемой задачи
8

9.

Парадоксы слайд 1/4 : Парадокс
Банаха-Тарского
• Парадокс удвоения шара: теорема в теории
множеств, утверждающая, что трёхмерный шар
равносоставлен двум своим копиям.
• Один шар делится на бесконечное множество
бесконечно малых частей, из которых можно
составить два конечных шара, равных исходному
• Следует заметить, что существование удвоения
шара по методу Банаха — Тарского, хотя и
кажется весьма подозрительным с точки зрения
повседневной интуиции, тем не менее не является
парадоксом в логическом смысле этого слова,
поскольку не приводит к логическому
противоречию.
9

10.

Парадоксы слайд 2/4 :
Парадокс лжеца
• Парадокс лжеца — утверждение «То, что я утверждаю
сейчас — ложно» (либо «Я лгу», либо «Данное
высказывание — ложь»).
• Если это высказывание истинно, значит, исходя из его
содержания, верно то, что данное высказывание — ложь;
но если оно — ложь, тогда то, что оно утверждает,
неверно; значит, неверно, что данное высказывание —
ложь, и, значит, данное высказывание истинно. Таким
образом, цепочка рассуждений возвращается в начало.
• Считается, что этот парадокс был сформулирован
представителем мегарской школы Евбулидом. Иногда это
называют парадоксом Эпименида, приписывая его
авторство Эпимениду.
• Это высказывание противоречит закону исключённого
третьего.
10

11.

Парадоксы слайд 3/4 :
Парадокс Рассела
Пусть К — множество всех множеств, которые не содержат себя в
качестве своего элемента. Содержит ли К само себя в качестве
элемента? Если предположить, что содержит, то получаем
противоречие с "Не содержат себя в качестве своего элемента". Если
предположить, что К не содержит себя как элемент, то вновь возникает
противоречие, ведь К — множество всех множеств, которые не
содержат себя в качестве своего элемента, а значит должно содержать
все возможные элементы, включая и себя.
Противоречие в парадоксе Рассела возникает из-за использования в
рассуждении внутренне противоречивого понятия множества всех
множеств и представления о возможности неограниченного
применения законов классической логики при работе с множествами.
Для преодоления этого парадокса было предложено несколько путей.
Наиболее известный состоит в предъявлении для теории множеств
непротиворечивой формализации , по отношению к которой являлись
бы допустимыми все «действительно нужные» (в некотором смысле)
способы оперирования с множествами. В рамках такой формализации
утверждение о существовании множества всех множеств было бы
невыводимым.
11

12.

Парадоксы слайд 4/4 :
Парадокс всемогущества
Парадо́кс всемогу́щества — семейство связанных парадоксов, имеющих отношение
к вопросу о том, что может сделать всемогущее существо, в особенности может ли
существо, которое в состоянии выполнить любое действие, сделать что-либо, что
ограничило бы его способность выполнять действия.
Общая современная версия парадокса всемогущества выражается в вопросе
«Может ли всемогущий создать такой камень, который не сможет поднять?».
Этот вопрос порождает дилемму. Всемогущий может или создать камень, который не
сможет поднять, или же не сможет создать такой камень. Если он сможет создать
такой камень, который не сможет поднять, тогда он перестанет быть всемогущим,
если же он не сможет это сделать, то он уже является не всемогущим.
Этот парадокс схож с другим классическим парадоксом, парадоксом непреодолимой
силы: Что произойдет, если человек, имеющий непреодолимую силу встретит
камень, который невозможно сдвинуть? Один из ответов на этот парадокс состоит в
том, что если существует непреодолимая сила, тогда по определению не существует
объекта, который не может быть сдвинут; и наоборот, если существует объект,
который невозможно сдвинуть, то никакая сила не может быть признана
непреодолимой. Но такие рассуждения не подходят к случаю всемогущества,
поскольку парадокс состоит в том, чтобы потребовать у всемогущего сделать
всемогущество невозможным. В контексте законности, парадокс всемогущества
иногда выражается в терминах законодательного всемогущества: власть может
12
создать любой закон в любое время

13.

Сравнение множеств
• Два множества равны между собой,
они состоят из одних и тех же элементов
если
– Свойства: для любых трех множеств X, Y, Z верно
• рефлексивность
X = X;
• коммутативность
• транзитивность
X = Y Y = X;
(X = Y) & (Y = Z) X = Z.
X Y, если x X и x Y;
– Свойства:
X Y, если X Y и X Y
(идемпотентность)
Множество X является подмножеством множества
Y, если любой элемент множества X принадлежит и
множеству Y.
• рефлексивность
X X
• транзитивность
X Y & Y Z, X Z
• свойства 0 и 1 Y U
13

14.

Универсум и пустое множество
• Пустое множество, обозначаемое
или {} есть множество, не содержащее
элементов
• Универсальное множество или
универсум есть множество,
элементами которого являются все
возможные элементы множества.
14

15.

Операции над множествами
• Объединение
A B = {x |x A x B}
• Пересечение
A B = {x |x A & x B}
• Разность
A\B = {x |x A & x B}
• Симметрическая разность
A/B = (A B)\(A B ) = {x | (x A & x B) (x A & x B)}
• Дополнение
A = {x | x A} = U\A, где
U - некоторый универсум.
15

16.

Объединение
• Объединением множеств А и В называется
множество, состоящее из всех тех и только тех
элементов, которые принадлежат хотя бы
одному из множеств А или В.
– Свойства
• рефлексивность
• коммутативность
• ассоциативность
• свойство 0
• свойство 1
А А=A
А В=В А
А (В С) = (А В) С = А В С
А =А
А U=U
А
В
16

17.

Пересечение
• Пересечением множеств А и В называется
множество, состоящее из всех тех и только тех
элементов, которые принадлежат как множеству А,
так и множеству В.
– Свойства
• рефлексивность А А = A
• коммутативность А В = В А
• ассоциативность А (В С) = (А В) С = А В С
• свойство 0
А =
• свойство 1
А U=А
А
А В
В17

18.

Разность
• Разностью множеств А и В называется
множество, состоящее из всех тех и только
тех элементов, которые принадлежат
множеству А и не принадлежат множеству В.
– Свойства
А\ =А
А\U=
• свойство 0
• свойство 1
\А=
U\А=A
А
А\В
В
18

19.

Симметрическая разность
• Симметрической разностью множеств А и
В называется множество, состоящее из всех
тех и только тех элементов, которые
принадлежат объединению множеств А и В,
и не принадлежат их пересечению.
– Свойства
• коммутативность А / В = В / А
• ассоциативность А / (В/С) = (А/В) / С = А / В / С
• свойство 0
А/ =А
• свойство 1
А/U=A
В
А
19

20.

Законы теории множеств
• Дистрибутивный
– A (B C) = (A B) (A C)
– A (B C) = (A B) (A C)
• Закон поглощения
– (A B) A = A
(A B) A = A
• Законы де Моргана
– A B A B
A B A B
• Выражение для разности
– A \ B = A B
20

21.

Декартово произведение
множеств, булеан, мощность
множества
• Булеаном множества А называется
множество всех подмножеств множества А и
обозначается как P(А)
• Декартовым произведением множеств А и
В называется множество, определяемое
следующим образом: А В = {(a,b) | a A &
b B}. Объект (a,b) называется
упорядоченной парой.
• Мощность множества |M| количество элементов множества
21

22.

Степень множества
• Степенью множества А называется его
прямое произведение самого на себя: Аn =
A A ... A.
n раз
Соответственно,
А0 = { }; А1 = A; А2 = A A;
• Теорема:
Аn = A An-1.
|A B| = |A| |B|.
22

23.

Проекция множества
• Кортеж – множество, для которого важен
порядок следования элементов
• Пусть А - множество, состоящее из
кортежей длины n, тогда проекцией
множества А называют множество
проекций кортежей из А.
(операция проекции может применяться только к
таким множествам, элементами которых являются
кортежи одинаковой длины).
– Если А = X Y, то Пр1А = Х, Пр2А = Y.
– Если А X Y, то Пр1А Х, Пр2А Y.
23

24.

Соответствия
• Соответствие - это множество пар вида
(a,b), образующихся при сопоставлении
заданным образом элементов множества А
элементам множества В, и сами
сопоставляемые множества А и В.
q = (A, B, Q),
Q A B.
– ПрАQ A называется областью
определения соответствия, или источником
соответствия.
– ПрВQ В называется областью значений
соответствия, или приемником.
– Множество пар Q, определяющих
соответствие, называется графиком
24
соответствия.

25.

Способы задания
соответствия
• В виде описания в соответствии с
определением
А={красный, желтый, зеленый}; B={стоять, идти};
А
Q={(красный, стоять),(зелёный, идти)}
• Графически
B
• В виде матрицы
A\B
стоять идти
красный
1
0
желтый
0
0
зелёный
0
1
25

26.

Обратное соответствие
• Соответствие, обозначаемое как q-1 = (B, A,Q-1),
где Q-1 B A, является обратным для
соответствия q=(A,B,Q), где Q A B, и
получается, если данное соответствие q
рассматривать в обратном направлении.
– Пример:
А={красный, желтый, зеленый}; B={стоять,
идти};
Q={(красный, стоять),(зеленый, идти)}.
Q-1={(стоять, красный),(идти, зеленый)}.
– Свойства:
(q-1)-1 = q.
26

27.

Композиция соответствий
• Композиция соответствий - это
операция
с 3-мя множествами А, В, С, на
которых заданы два соответствия
q = (A, B, Q), где Q A B и
р = (В, С, Р), где Р B C,
причем область значений первого
соответствия q совпадает с областью
определения второго р
Пр2Q = Пр1Р.
• Обозначение:
27
q(p) = (A, C, Q P), Q P A C.

28.

Отображения
• Полностью определенное на множестве
источнике соответствие q(A,B,Q) (где множество А есть область определения данного соответствия q)
называется отображением множества А в
множество В.
• Обозначения
– Г: А В = (А,В,Г), где Г А В, ПрАГ = А или
(А,В,Г), Г А В | a A b B
• Каждому элементу x A отображение Г ставит в
соответствие подмножество Г(x) В, которое
называют образом элемента x.
• Пусть X A; x X, Г(x) В – образ элемента х,
тогда Г(Х) = Г ( х ) – образ множества Х
х Х
28

29.

Отображения
• Отображение i : X X называется
тождественным, если I(x) = x для всех х Х,
и обозначается как idX или как 1Х.
Свойство:
Для любого отображения Г : X Y имеет место
1Y g = g 1X = g.
• Отображение Г : X Y называется инъекцией,
если для любых 2-х x1,x2 X из равенства
Г(x1)=Г(x2) следует x1=x2.
• Отображение Г : X Y называется сюръекцией,
если для каждого y Y существует такой x X, что
y=Г(x).
• Отображение Г : X Y называется биекцией, если
оно одновременно является инъекцией и
29
сюръекцией.

30.

Примеры
А
а1
В
b1
а2
А
b2
а3
b3
а4
b4
Соответствие
А
а1
а2
b1
b2
а3
а4
В
b3
b4
Инъекция
b3
а4
b4
В
b1
а2
b2
а3
а1
Отображение
А
а1
а2
а1
а2
b3
b4
Биекция
В
b1
b2
а3
b2
а3
а4
В
b1
А
а4
b3
b4
Сюръекция
30

31.

Свойства отображений
• Если
Х1 А и Х2 А, то
Г ( X1 X 2 ) Г ( X1 ) Г ( X 2 )
• Если
Х1 А и Х2 А, то
Г ( X1 X 2 ) Г ( X1 ) Г ( X 2 ) – верно
только в случае однозначного
отображения.
31

32.

Частный случай отображения
• Отображение вида Г: А А является частным
случаем отображения Г: А В, при А=В,
представляет собой отображение множества А
в себя самого и определяется парой (А, Г), где
Г А2.
• Композицией 2-х отображений вида Г:А А и
:А А называется отображение Г ,
определяемое как (Г )(х) = Г( (х)).
• Если Г= , то Г2(х)=Г(Г(х)), Г3(х)=Г(Г2(х)), …
Гn(х)=Г(Гn-1(х)); Г0(х)=Г(Г-1(х))=(ГГ-1)(х)=x
32

33.

Функции
• Однозначное отображение f:X Y
называется функцией. Однозначность
означает, что для любых пар (x1,y1) f и
(x2,y2) f из x1 = x2 следует y1 = y2.
• Если Y R, то функция f называется
функцией с вещественными значениями.
• Для любых пар (x,y) f
y = f(x).
• Формальное определение
f = { (x,y) X Y | y = f(x) }
33

34.

Способы задания функций
• Перечисление пар (х,у)
• Формула преобразования х в у
• График функции
34

35.

Функции многих переменных
• Если в выражении
Х=U V,
то имеем функцию 2-х переменных f(u,v), где
u U, v V.
• Или формально
f = { (u,v,y) U V Y | y = f(u,v) }
• Функция n переменных
f = { (x1,x2,…,xn,y) X1 X2 … Xn Y | y = f(x1,x2,…,xn) }
f:X Y
35

36.

Операции над функциями
• Обратная функция
f-1: Y X
• Композиция функций
если f: X Y, g: Y Z, то f g: X Z
z = (f g)(x) = g(f(x))
36

37.

Функционал
• Функционал устанавливает
зависимость между множеством чисел
и некоторым множеством функций (т.е.
это зависимость числа от функции)
• Например, определенный интеграл
b
J ( f ) f ( x )dx
число
a
функция
37

38.

Оператор
• Оператор устанавливает
соответствие между двумя
множествами функций, каждой
функции одного множества ставится
в соответствие определенная
функция другого множества.
df
f ( x )
[ f ( x )]
dx
Оператор дифференцирования
38

39.

Отношения
• Термин «отношение» обозначает некоторые виды
соответствий, заданные на одном множестве.
• Если задано соответствие (Х,R),
то о элементе у R(х) говорят, что он находится в
отношении R к элементу х: у R х.
• Отношением называется пара множеств
(Х,R), где R Хn.
• Элементами множества Хn являются упорядоченные
n-ки, и такое отношение называют n-арным или nместным; множество упорядоченных пар элементов
называют бинарным, упорядоченных троек тернарным.
39

40.

Отношения
Если R A2 - отношение, заданное на множестве
А, то
• Обратное отношение R-1={(a,b) | (b,a) R}
• Дополнение отношения R ={(a,b) | (a,b) R}
• Тождественное отношение I = {(a,a) | a A}
• Универсальное отношение
U= {(a,b) | a A & b A}
[U = A2]
• Ядро отношения
O = R° R-1
40

41.

Свойства отношений
• Рефлексивность
хRхистинно ;
• Антирефлексивность
хRх
ложно;
• Симметричность
хRу уRх;
• Антисимметричность
(х R у)&(у R х) x=y ;
• Несимметричность
(полнота, или
линейность)
Если (х R у) – истинно, то (у R х) – ложно;
• Транзитивность
(х R у)&(у R z) x R z .
41

42.

Теорема о свойствах
отношений
• Если R A A - отношение на множестве
А, то тогда
– R - рефлексивно
– R - антирефлексивно
– R - симметрично
– R - антисимметрично
I R;
R I = ;
R = R-1;
R R-1 I;
– R - несимметрично
= U;
(полно) R I R-1
– R - транзитивно
R ° R R;
42

43.

Отношение эквивалентности
• Отношение является отношением
эквивалентности, если оно рефлексивно,
симметрично и транзитивно.
• Элементы множества рассматриваются как
эквивалентные тогда, когда любой из этих
элементов при некотором рассмотрении может
быть заменен другим.
• Например,
на множестве студентов – отношение «быть в
одной группе» или «быть на одном курсе»;
на множестве целых чисел – «иметь
одинаковый остаток при делении на число n». 43

44.

Классы эквивалентности
• Если на множестве Х определено отношение
эквивалентности, то подмножество элементов,
эквивалентных некоторому элементу х Х,
называют классом эквивалентности.
• {Aj X | j = 1 n} – множество классов
эквивалентности для множества Х.
Так как все элементы одного класса эквивалентности
эквивалентны между собой, то всякий элемент х Х может
находиться только в одном классе. Х будет являться
объединением непересекающихся множеств Аj, так что
полная система классов {Aj X | j = 1 n} – есть разбиение
множества Х.
• Каждому отношению эквивалентности на
множестве Х соответствует некоторое разбиение
множества Х на классы эквивалентности Aj. 44

45.

Отношения порядка
• Отношения порядка определяют порядок
расположения элементов множества.
• Отношение является отношением
нестрого порядка, если оно рефлексивно,
антисимметрично и транзитивно ( , , , ).
• Отношение является отношением
строго порядка, если оно
антирефлексивно, несимметрично и транзитивно
(<, , >, , ).
• Множество Х называется упорядоченным, если
сравнимы между собой любые 2 его элемента,
то есть для них имеет место
x < y или x = y или x > y
45

46.

Отношение доминирования
• Между элементами множества Х
имеет место отношение
доминирования, если эти элементы
обладают следующими свойствами:
– Антирефлексивность (никакой
элемент не может доминировать над
самим собой).
– Несимметричность (в каждой паре
элементов только один из них может
доминировать над другим).
46

47.

Реализация множеств
• Посредством двоичного вектора
• Массив
• Связанный список
• Последовательность
47

48.

Двоичный вектор
Недостатки: ограниченность количества элементов множества,
необходимость упорядочивания элементов множества
48

49.

Массив
• Количество элементов множества ограничено
размером массива
• Время поиска элемента определяется размером
массива (справедливо для неупорядоченных
массивов)
• Для хранения массива необходимо выделять память
(частично справедливо для динамических массивов)
• Более сложная реализация операций над
множествами
49

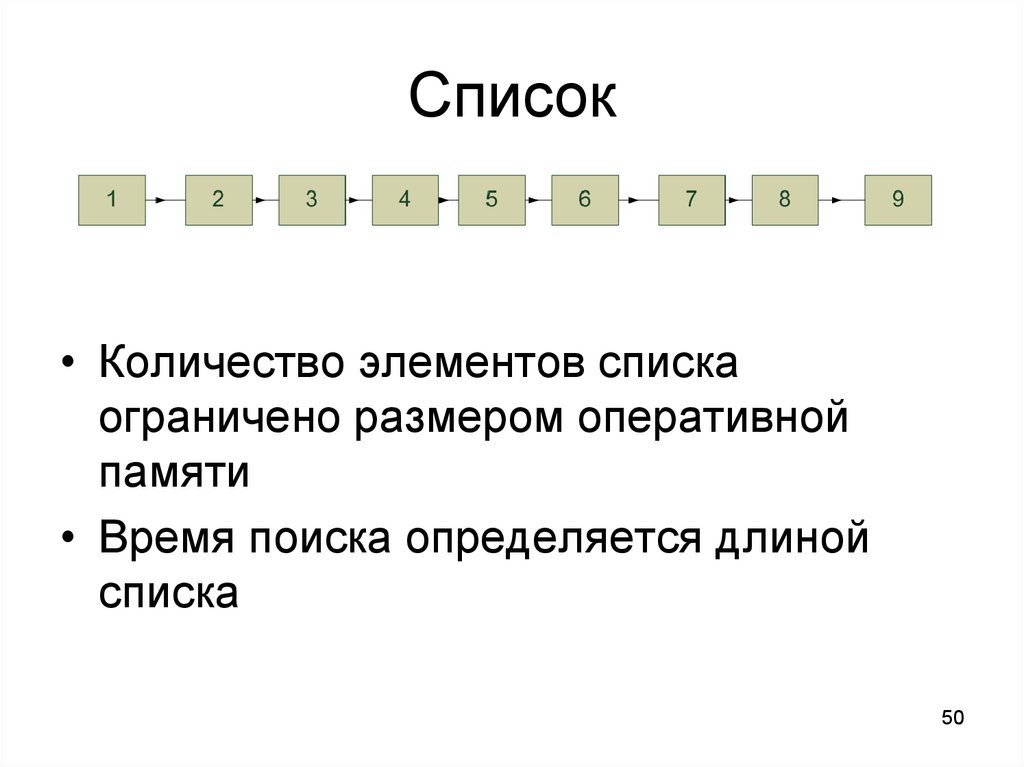
50.

Список
• Количество элементов списка
ограничено размером оперативной
памяти
• Время поиска определяется длиной
списка
50

51.

Класс HashSet<T> и
последовательности
• HashSet<T> - универсальный класс, содержащий
основные операции над множествами
• Последовательность – Sequence – способ
представления бесконечных множеств в
функциональном программировании
• Задача: найти индекс элемента последовательности
Фибоначчи, содержащего 1000 разрядов в его
строковой записи.
let res =
2+(Seq.unfold ( fun (u, v) -> Some (v, (v, v + u)) ) (1I,1I)
|> Seq.findIndex (fun x -> x.ToString().Length = 1000))
51

52.

Применение множеств
• Словарь
• Хэш – таблицы
• Очередь с приоритетами
• Отношение «многие – ко – многим» и
мультисписки
• Деревья двоичного поиска
52

53.

Словарь
• Часто возникает задача проверить
наличие в множестве некоторого
элемента. Для таких целей
используется словарь, который может
быть как упорядоченным, так и
неупорядоченным.
• Dictionary<TKey, Tvalue>
• Недостаток: быстрый рост времени
выполнения поиска по мере роста
словаря
53

54.

Хэш - таблица
• Множество разбивается на подмножества,
называемые сегментами. Задаётся хэш –
функция, принимающая уникальное значение
для каждого сегмента.
• Открытое хеширование – в таблице
сегментов хранятся значение хэш – функции
и указатель на список элементов сегмента
• Закрытое хеширование – элементы сегмента
хранятся в таблице сегментов
54

55.

Хэш-таблица
55

56.

Очереди с приоритетом
• На множестве элементов задана
функция приоритета, принимающая
целочисленные значения или значения
из линейно упорядоченного множества
• Пример: планирование разделения
времени процессора, приоритеты при
передаче данных
• Реализация – связанный список,
частично упорядоченное дерево
56

57.

Отношение «многие – ко –
многим» и мультисписки
• Мультисписок – структура, в которой
каждый элемент имеет более одного
указателя и может принадлежать
одновременно нескольким спискам
• Пример – список учебных курсов и
посещающих их студентов
57

58.

Деревья двоичного поиска
• Дерево, узлы которого хранят элементы
множества.
• Все элементы, хранящиеся в узлах
левого поддерева любого элемента x
всегда меньше x, а узлы правого
поддерева – всегда больше x.
• Если обойти дерево во внутреннем
(симметричном) порядке, то
полученный список будет отсортирован
в соответствии с заданным отношением
порядка
58

59.

Двоичное дерево
59