Системы счисления

1.

Системы счисления

2.

Понятие
Система счисления – это способ записи чисел по определенным
правилам с помощью специальных знаков – цифр.
Знаки (символы), используемые в СС для обозначения чисел,
называются цифрами.
Алфавит – это набор цифр.

3.

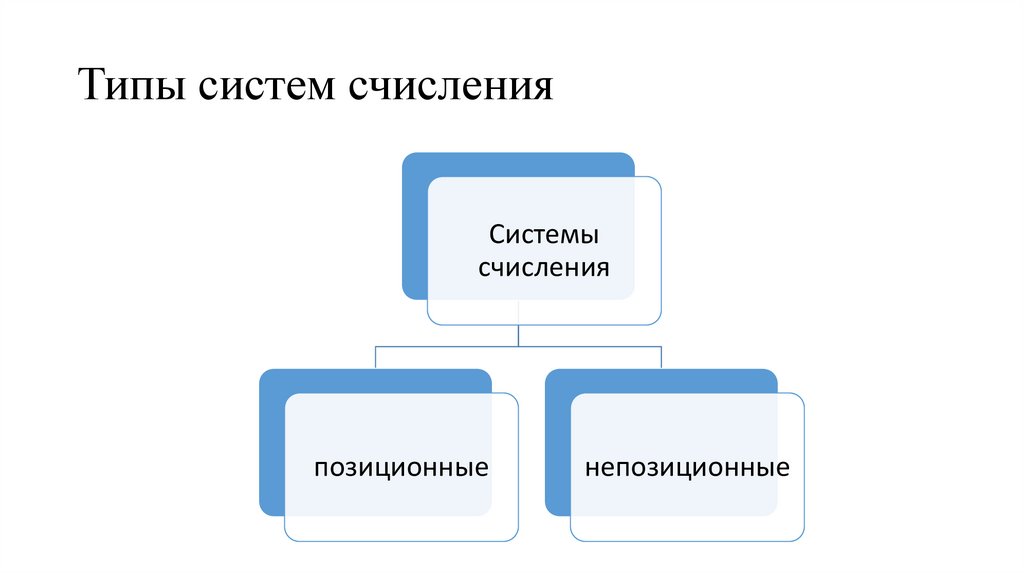
Типы систем счисления
Системы
счисления
позиционные
непозиционные

4.

Непозиционные системы счисления
Римская система счисления - непозиционная система счисления,
в которой для записи чисел используются буквы латинского
алфавита:
1 - I, 5 - V, 10 - X, 50 - L, 100 - C, 500 - D и 1000 - M.
черта над цифрой увеличивает ее значение в 1 000 раз:

5.

Правила записи чисел
Для правильной записи больших чисел римскими цифрами
необходимо сначала записать число тысяч, затем сотен, затем
десятков и, наконец, единиц.
Натуральные числа записываются при помощи повторения этих цифр.
При этом, если большая цифра стоит перед меньшей, то они
добавляются (принцип сложения), если же меньшая – перед большей,
то меньшая вычитается из большей (принцип вычитания). Последнее
правило применяется только во избежание четырехкратного повторения
одной цифры. Например, I, Х, С ставятся соответственно перед Х, С, М
для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400.
Например, VI = 5 + 1 = 6, IV = 5 - 1 = 4 (вместо IIII); XIX = 10 + 10 – 1 =
19 (вместо XVIIII), XL = 50 - 10 = 40 (вместо XXXX).

6.

Позиционные системы счисления
Арабская(Десятичная) система счисления состоит из 10 цифр
0123456789
В позиционных системах значение каждой цифры определяется её
позицией в записи числа.
Любое число десятичной системы представляется в виде:
765=700+60+5=7*100+6*10+5*1=7*102+6*101+5*100
76.54=7*10+6*1+5*0,1+4*0,01=7*101+6*100+5*10-1+4*10-2

7.

Позиционные системы счисления
Двоичная система счисления состоящая из 2 цифр:
0и1
Пример:
100010012=13710

8.

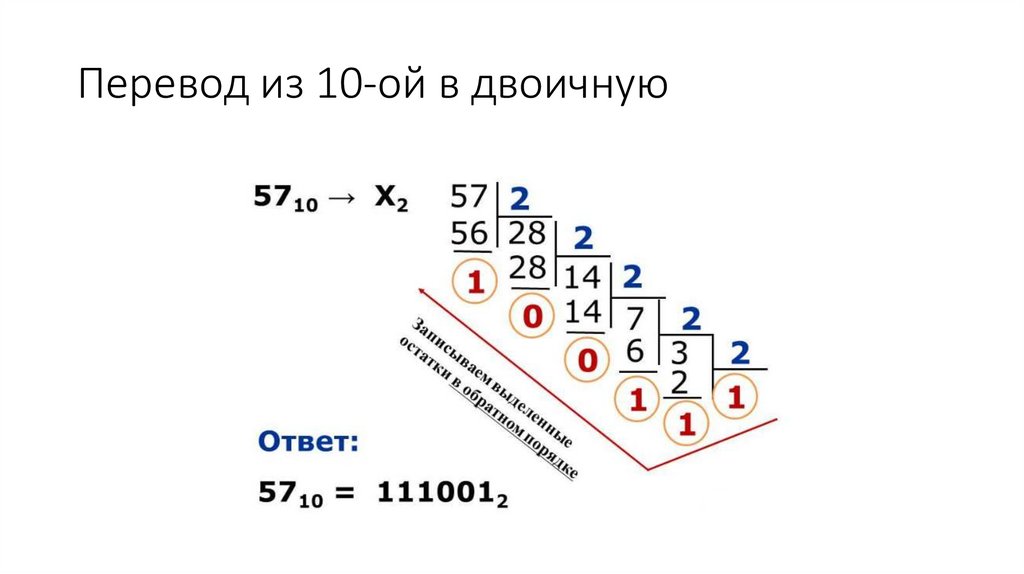
Перевод из 10-ой в двоичную
Правила перевода
• Разделить десятичное число на 2. Получится частное и остаток.
• Частное опять разделить на 2. Выполнять деление до тех пор,
пока последнее частное не станет меньшим 2.
• Записать последнее частное и все остатки в обратном порядке.
Полученное число и будет двоичной записью исходного
десятичного числа.

9.

Перевод из 10-ой в двоичную

10.

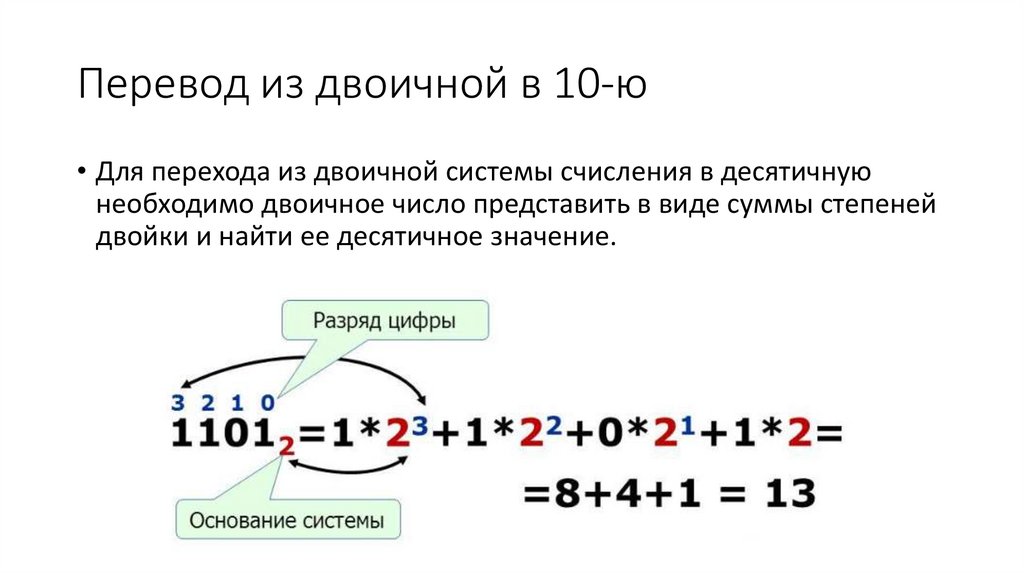
Перевод из двоичной в 10-ю
• Для перехода из двоичной системы счисления в десятичную
необходимо двоичное число представить в виде суммы степеней
двойки и найти ее десятичное значение.

11.

Самостоятельная часть
1. Распишите число в развернутой форме: 458,2373,93710
2. Представить римские числа в десятичной системе счисления:
CDIX,CVXLIX,MCCXIX.
3. Перевести число в двоичную систему: 458,2373,93710.
4. Перевести число в десятеричную систему: 1101,10010,1010101