Похожие презентации:
Aibės, veiksmai su aibėmis
1. Aibės
2.
Aibė yra jos elementų visumaPavyzdžiai
Elementų tvarka
nėra svarbi:
A = {1, 2, 3, 4};
B = {a, ą, e, ė, ę, i, į, y, u, ų, ū};
C = {Onutė, Marytė};
{1, 2, 3} = {2, 3, 1}
= {3, 1, 2} = …
D = {1, 2, 3, …, n};
E = {1, 8, 27, …, k3, …};
F = { x: x turi savybę P}
(Taip pat rašoma
F = { x | x turi savybę P},
F = { x: P(x)}, ir t.t. )
3.
• Aibę sudarantys objektai vadinami aibės elementais.Žymima: a, b, c, d, x, y, …. (mažosiomis raidėmis)
• Pagal elementų skaičių aibės skirstomos į baigtines
(šių aibių elementus galima išvardyti) ir begalines
(elementų išvardyti negalima).
Pavyzdžiui,
skaičių aibė A={-1; 0; 1} turi tris elementus – skaičius -1,
0 ir 1. Ši aibė A yra baigtinė.
N ={1; 2; 3; ...} - natūraliųjų skaičių aibė yra begalinė.
4.
Jeigu a yra aibės A elementas (įeina į aibę A), tai rašomaa A
Jeigu a nėra aibės A elementas, tai rašoma
a A.
Pavyzdžiui, 1 ∈ {0, 1, 3, 5} ir 2 {0, 1, 3, 5}.
Paminėkime gerai žinomas matematikoje skaičių aibes:
N = {1, 2, 3, . . .} – natūralieji skaičiai,
Z = {...,−2, −1, 0, 1, 2, 3, . . .} – sveikieji skaičiai,
Q = { m/n , m ∈ Z, n ∈ N} – racionalieji skaičiai,
R – realieji skaičiai.
5.
6.
7.
8.
Aibės A ir B yra lygios (rašoma A = B), jeiguA B ir B A.
9.
Tuščia aibė neturi elementų. Ji žymima arba {}.Pavyzdžiui,
{1, 2} ∩ {3, 4, 5} = ∅
{x ∈ R : x2 + 1 = 0} = ∅
Universali aibė (U arba I) – visos nagrinėjamos aibės yra
jos poaibiai.
10.
Pavyzdžiai1. Nurodyti aibės A elementus, jeigu
A = {x : x – sveikas skaičius ir x2 < 30}
A = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
11.
2. Nurodyti aibės poaibius:a) {a};
a) , {a};
b) {a, b};
b) , {a}, {b}, {a, b};
c) {a, b, c};
c) , {a}, {b}, {c}, {a, b},
{a, c}, {b, c}, {a, b, c};
d)
d) ;
12.
3. Ar teisingi teiginiai?a) ;
a) taip;
b) ;
b) ne;
c) A;
A- bet kuri aibė
c) taip;
d) A;
A- bet kuri aibė
d) ne;
e) {2} {1, 2, 3};
e) ne;
f) {2} {1, {2}, 3};
f) taip;
g) {2} {1, 2, 3};
g) taip;
h) {2} {1, {2}, 3};
h) ne;
i) = { };
i) ne;
j) { }.
j) taip.
13.
4. Kiek elementų sudaro aibę?a) { , { }};
a) du;
b) {{ , { }}};
b) vienas;
c) {1, 2, 3, {1, 2, 3}};
c) keturi;
d) { , { }, { , { }}};
d) trys;
e) { , { }, a, b, {a, b}, {a, b,
{a, b}}}.
e) šeši.
14. Veiksmai su aibėmis
15.
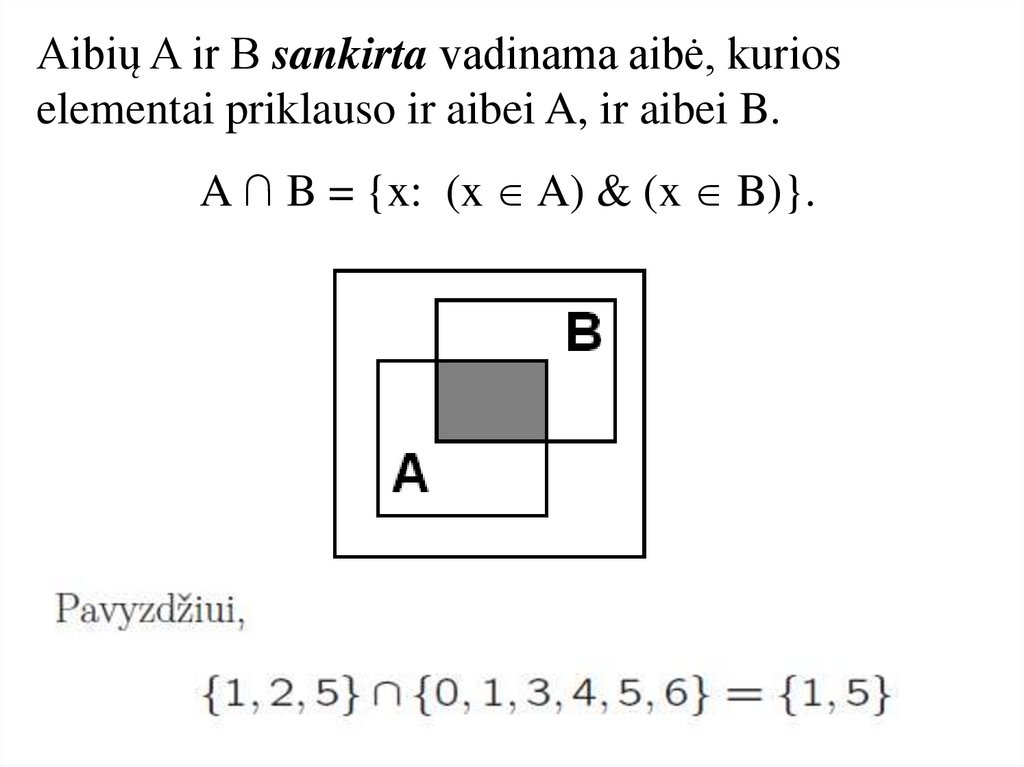
Aibių A ir B sankirta vadinama aibė, kurioselementai priklauso ir aibei A, ir aibei B.
A ∩ B = {x: (x A) & (x B)}.
16.
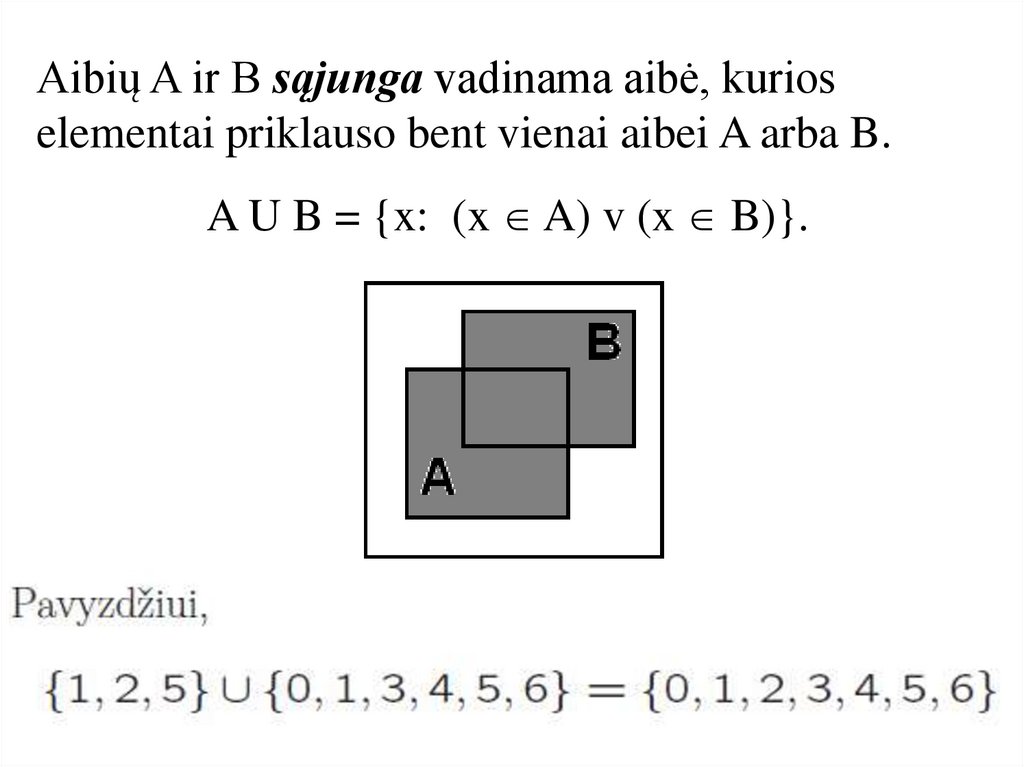
Aibių A ir B sąjunga vadinama aibė, kurioselementai priklauso bent vienai aibei A arba B.
A U B = {x: (x A) v (x B)}.
17.
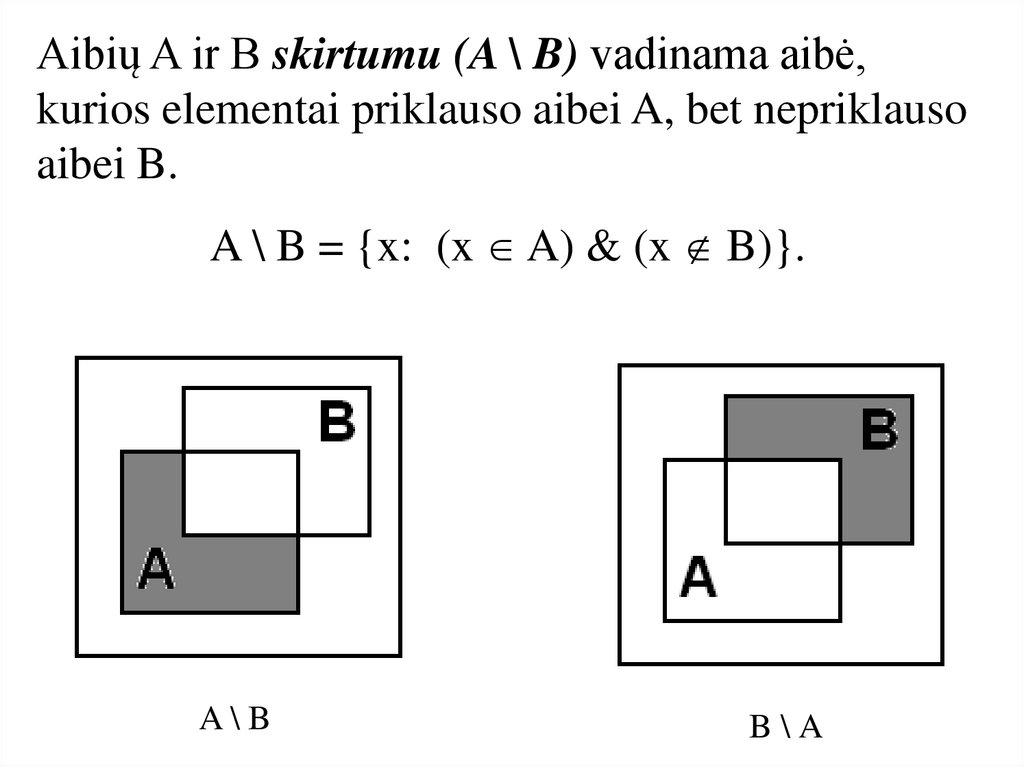
Aibių A ir B skirtumu (A \ B) vadinama aibė,kurios elementai priklauso aibei A, bet nepriklauso
aibei B.
A \ B = {x: (x A) & (x B)}.
A\B
B\A
18.
19.
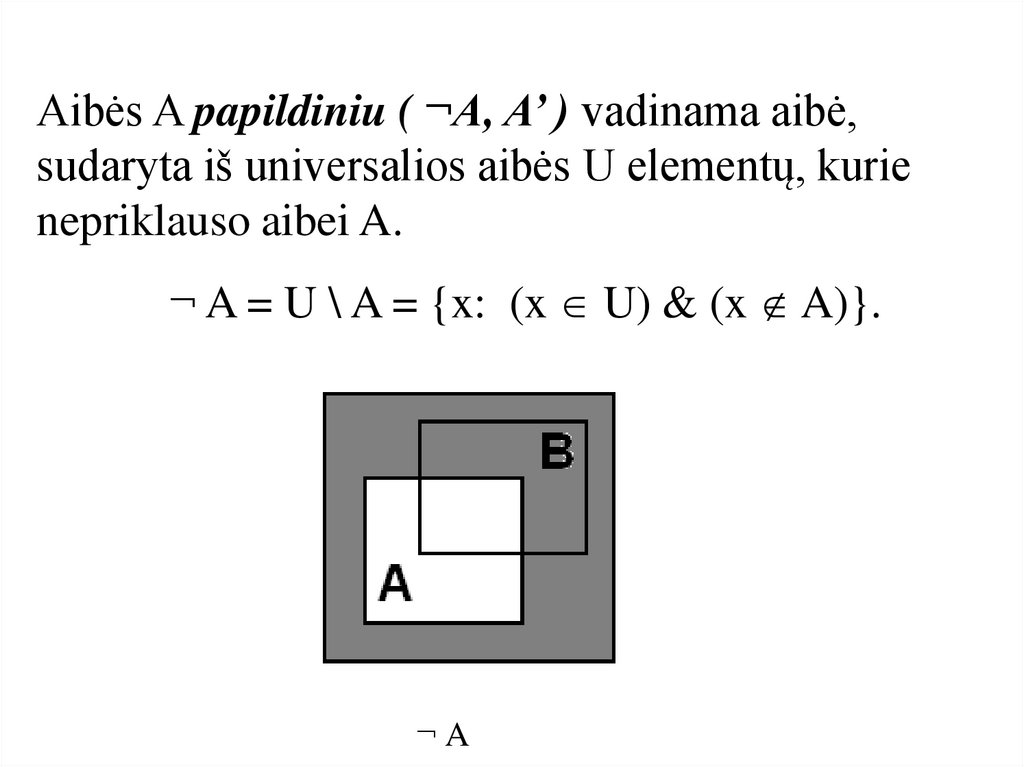
Aibės A papildiniu ( ¬A, A’ ) vadinama aibė,sudaryta iš universalios aibės U elementų, kurie
nepriklauso aibei A.
¬ A = U \ A = {x: (x U) & (x A)}.
¬A
20.
PavyzdžiaiTegul A = {1, 2, 3, 4, 5, 6, 7}, B = {4, 5, 6, 7, 8, 9, 10}, C
= {2, 4, 6, 8, 10}, U = {1, 2, 3, 4, 5, 6, 7 , 8, 9, 10}.
Raskite
a) A C;
a) {1, 2, 3, 4, 5, 6, 7, 8, 10};
b) A B;
b) {4, 5, 6, 7};
c) A (B C);
c) {2, 4, 5, 6, 7};
d) (A B) C;
d) {2, 4, 5, 6, 7, 8, 10};
e) ¬ (A B);
e) {1, 2, 3, 8, 9, 10};
f) ¬ A ¬ B;
f) ;
g) (A B) \ (A B);
g) {1, 2, 3, 8, 9, 10};
h) A \ B.
h) {1, 2, 3}.
21.
PavyzdžiaiTegul A = {1, 2, 3, 4, 5, 6, 7}, B = {4, 5, 6, 7, 8, 9, 10}, C = {2, 4,
6, 8, 10}, U = {1, 2, 3, 4, 5, 6, 7 , 8, 9, 10}.
Raskite
a) A \ C;
a) {1, 3, 5, 7};
b) (A \ B) (B \ A);
b) {1, 2, 3, 8, 9, 10};
c) A (B ¬ C);
c) {5, 7};
d) (A B) \ ¬ B;
d) {4, 5, 6, 7 , 8, 9, 10};
e) (A \ ) (A \ A);
e) {1, 2, 3, 4, 5, 6, 7};
f) ¬ A ¬ B.
f) .
22.
Kurie teiginiai teisingi?a) A = A;
a) ne;
b) Jeigu A B, tai A B = A;
b) taip;
c) Jeigu A B = A, tai A B;
c) taip;
d) A \ A = A;
d) ne;
e) A = A;
e) taip;
f) Jeigu A B, tai A B = A;
f) ne;
g) A \ = A;
g) taip;
h) Jeigu A B = A, tai B A.
h) taip;
23.
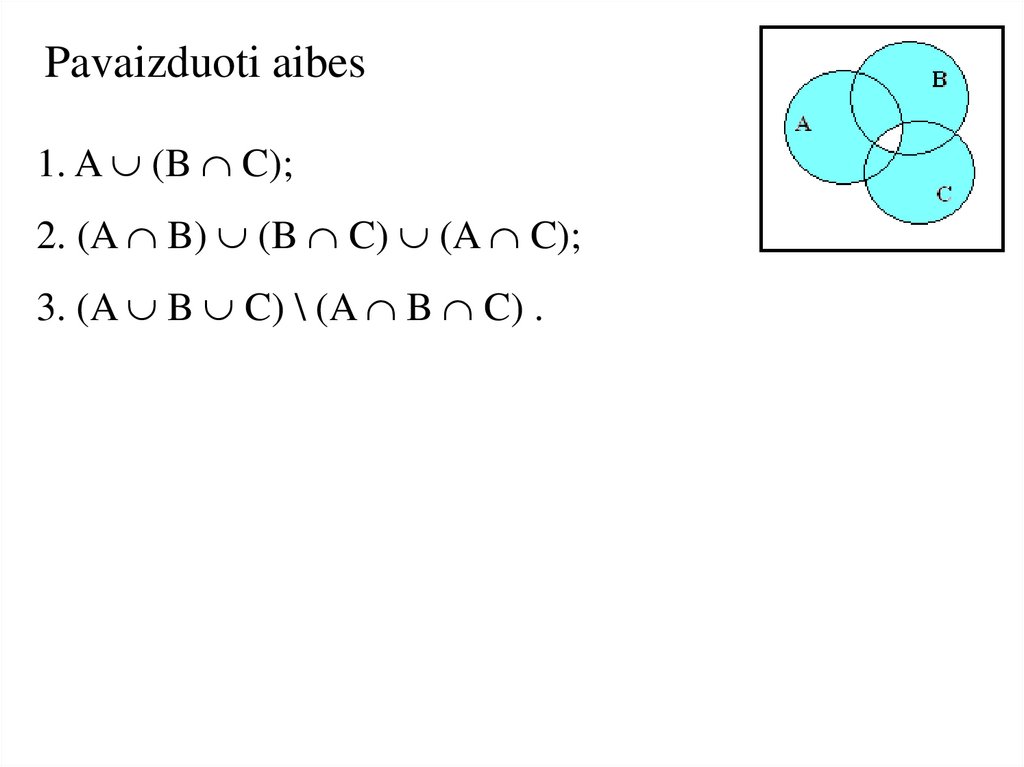
Pavaizduoti aibes1. A (B C);
2. (A B) (B C) (A C);
3. (A B C) \ (A B C) .
24.
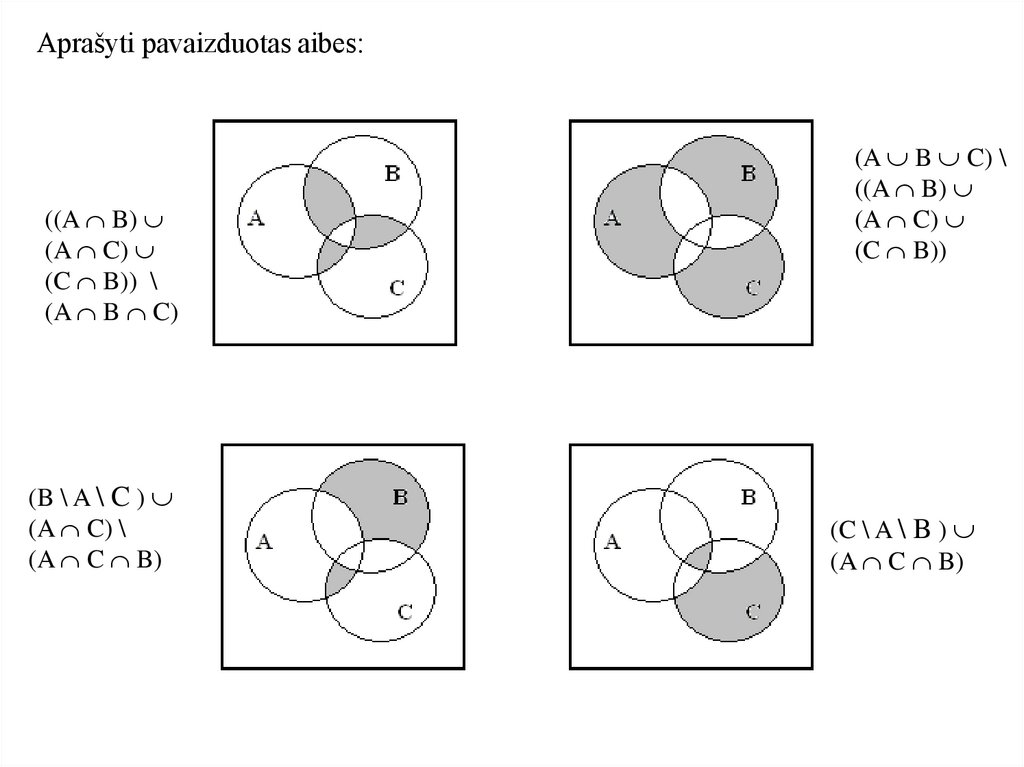
Aprašyti pavaizduotas aibes:((A B)
(A C)
(C B)) \
(A B C)
(B \ A \ C )
(A C) \
(A C B)
(A B C) \
((A B)
(A C)
(C B))
(C \ A \ B )
(A C B)
25. Operacijų su aibėmis savybės
26.
Komutatyvumo dėsniaiA B=B A
A B=B A
Asociatyvumo dėsniai
(A B) C = A (B C)
(A B) C = A (B C)
Distributyvumo dėsniai
A (B C) = (A B) (A C)
A (B C) = (A B) (A C)
27.
De Morgano dėsniai¬ (A B) = ¬A ¬ B
¬ (A B) = ¬A ¬ B
A U =A
A =A
A ¬A=U
Idempotentumo dėsniai
A ¬A=
A A=A
¬ (¬ A) = A
A A=A
28.
Įrodysime distributyvumo dėsnį:A (B C) = (A B) (A C)










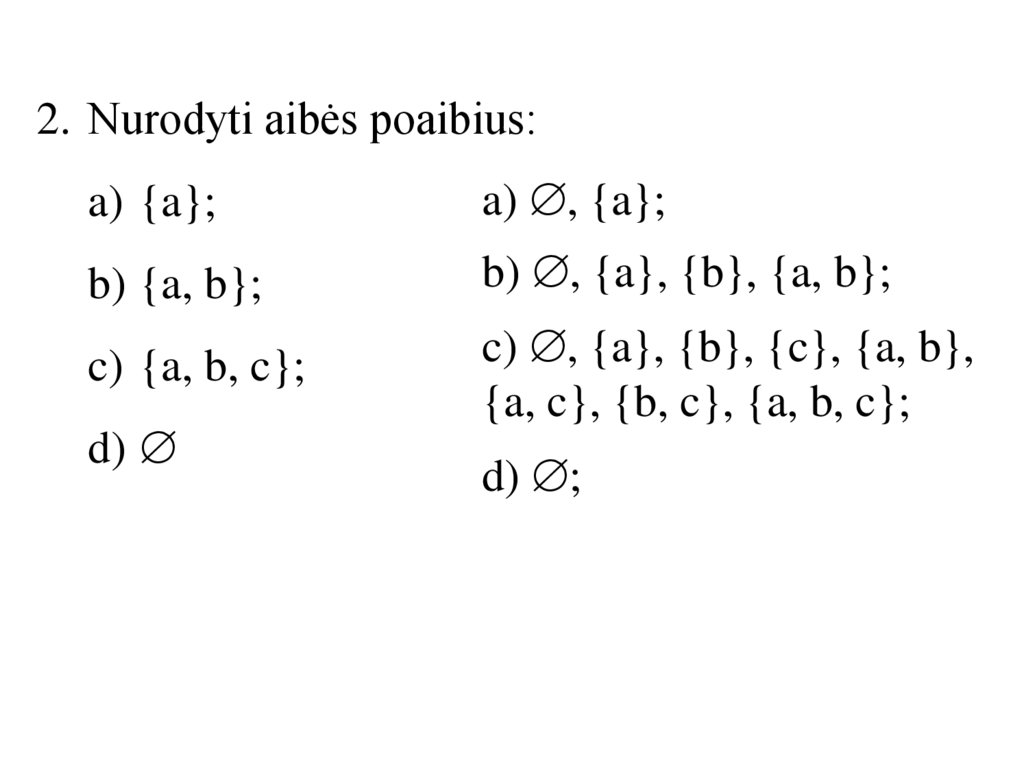











 Математика
Математика