Предел функции

2.12M

Категория: $Математика$ Математика

Похожие презентации:

Предел функции

1. Предел функции

2. Предел функции в точке

Пусть функция y = f(x) определена в некоторой окрестности точки x0,
кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x) A
x x0

3. Предел функции в точке

0; 0; x : x x0 f ( x ) A
ε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ –
окрестности точки x0 точки графика функции лежат
внутри полосы, шириной 2ε, ограниченной прямыми: у
=А+ε,у=А-ε.

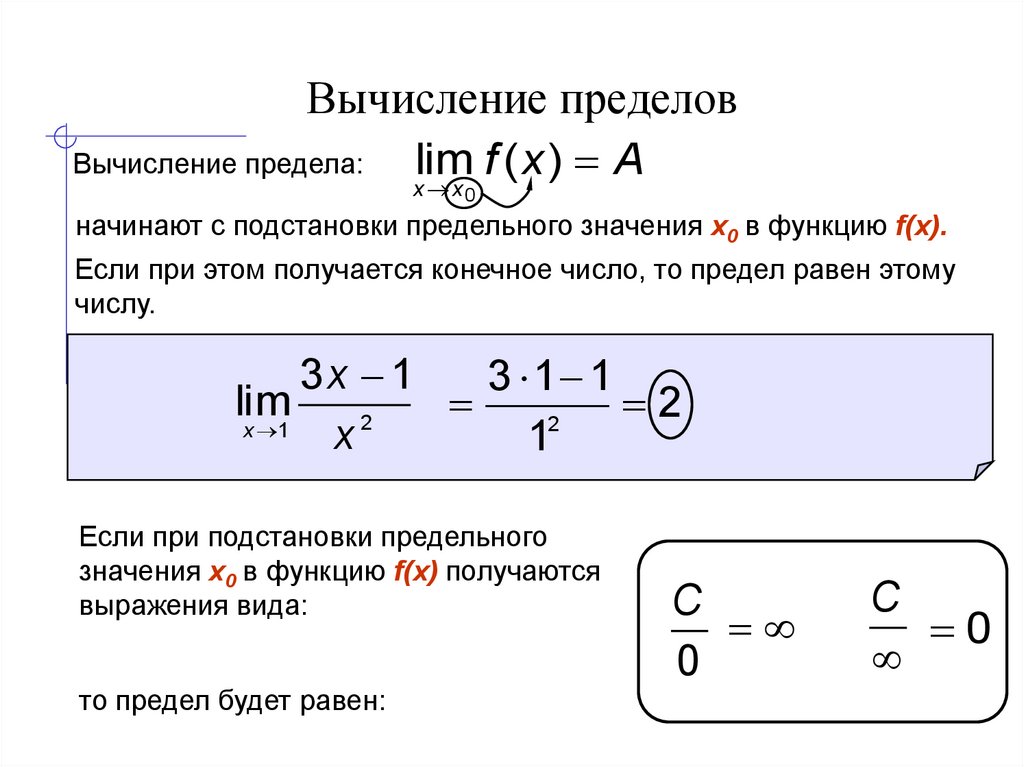
4. Вычисление пределов

Вычисление предела:
lim
f
(
x
)
A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0

5. Вычисление пределов

Часто при подстановке предельного значения x0 в функцию f(x)
получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.

6. Раскрытие неопределенностей

Раскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
необходимо разложить
наlim
lim
Если f(x) – иррациональная
x 0
x 0
0
x
множители
числитель
и
x 1 умножить
1
дробь, x
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2

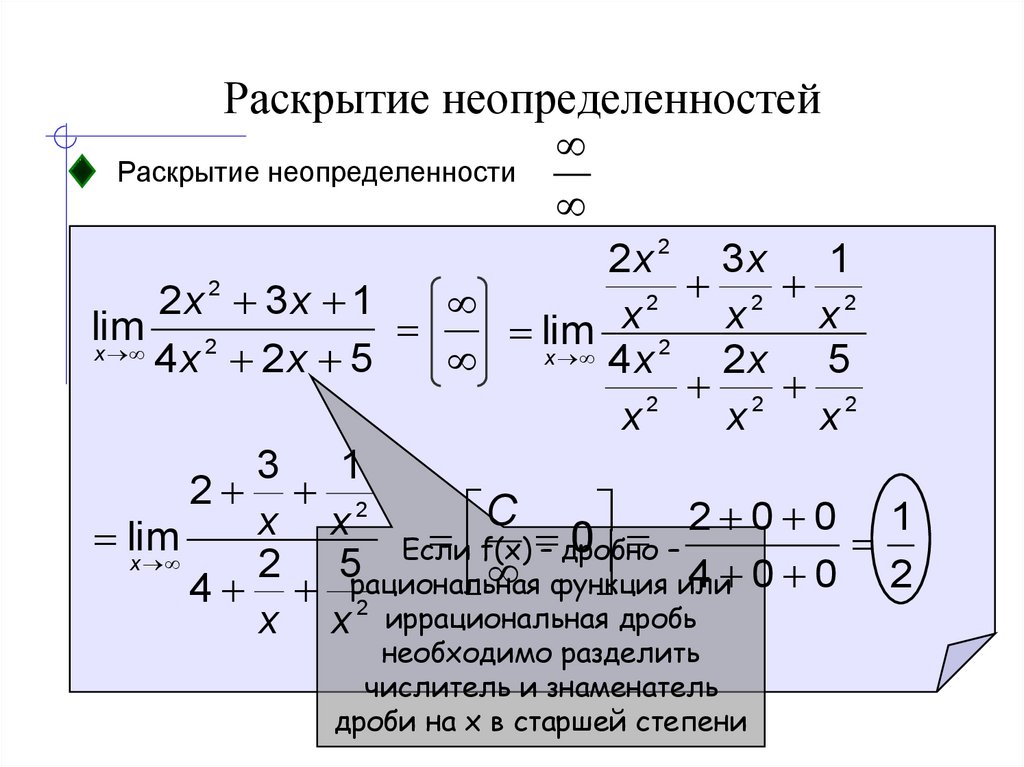
7. Раскрытие неопределенностей

Раскрытие неопределенности
2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
x
x 4 x 2
4 x 2 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени

8. Раскрытие неопределенностей

Раскрытие неопределенности
2
2
lim
x
1
x
1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
lim
x
2
2
2
2
2
Умножим и разделим
2
( x 1) ( x функцию
1)
на
сопряженное
lim
2
x
2
2
выражение.
2
2
x 1 x 1
2
0
x 1 x 1
2