Похожие презентации:
Лекция №9. Тема 4. Статистические методы обработки результатов измерений и контроля качества
1.
Лекция № 9Тема 4. Статистические методы обработки
результатов измерений и контроля качества
4.6. Обработка результатов косвенных
измерений
4.7. Обработка результатов совместных
измерений
2.
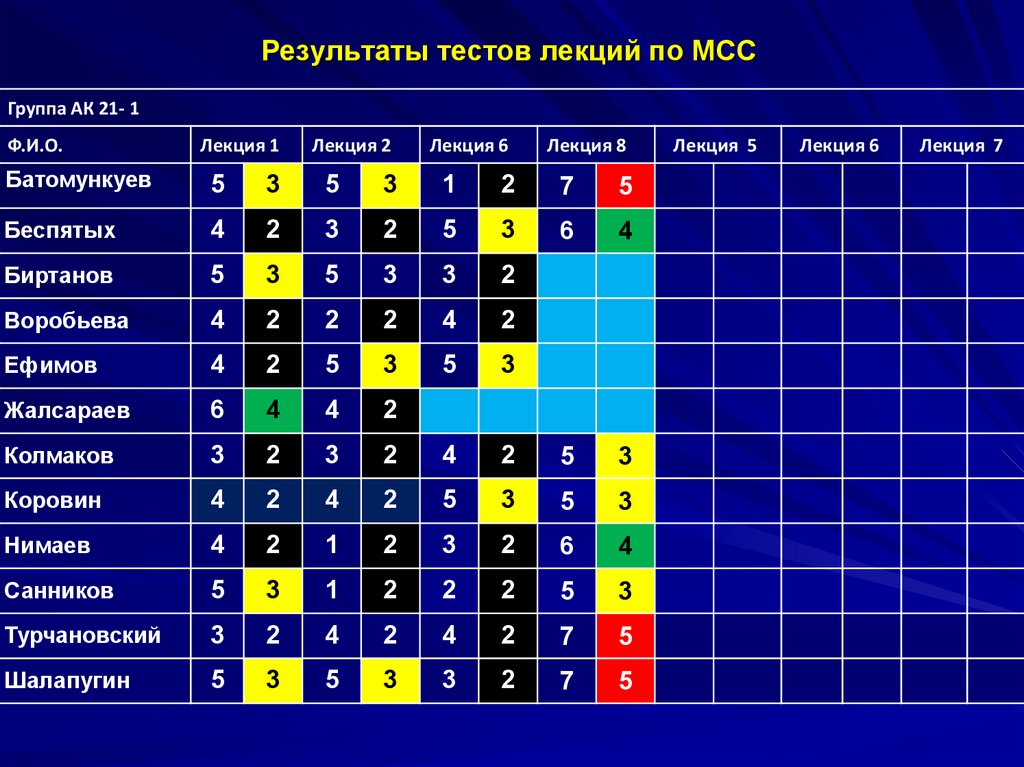
Результаты тестов лекций по МССГруппа АК 21- 1
Ф.И.О.
Лекция 1
Лекция 2
Лекция 6
Лекция 8
Батомункуев
5
3
5
3
1
2
7
5
Беспятых
4
2
3
2
5
3
6
4
Биртанов
5
3
5
3
3
2
Воробьева
4
2
2
2
4
2
Ефимов
4
2
5
3
5
3
Жалсараев
6
4
4
2
Колмаков
3
2
3
2
4
2
5
3
Коровин
4
2
4
2
5
3
5
3
Нимаев
4
2
1
2
3
2
6
4
Санников
5
3
1
2
2
2
5
3
Турчановский
3
2
4
2
4
2
7
5
Шалапугин
5
3
5
3
3
2
7
5
Лекция 5
Лекция 6
Лекция 7
3.
4.6. Обработка результатов косвенных измерений13
При косвенных измерениях искомое значение величины
находят расчетом на основе измерения других величин,
связанных с измеряемой величиной известной зависимостью
А f x1 ,..., xm .
Результатом косвенного измерения является оценка
величины А , которую находят подстановкой в формулу
оценок аргументов xi .
Линейные косвенные
измерения
m
А bi xi
i 1
Погрешности измерения аргументов могут быть заданы
своими границами , либо доверительными границами с
доверительными вероятностями Рi.
При малом числе аргументов (меньше пяти) простая оценка
погрешности результата получается суммированием предельных
погрешностей
A x1 x2 ... xm
(m < 5)
4.
4.6. Обработка результатов косвенных измерений12
Однако эта оценка является излишне завышенной,
поскольку такое суммирование фактически означает, что
погрешности измерения всех аргументов одновременно
имеют максимальное значение и совпадают по знаку.
Вероятность такого совпадения практически равна нулю. Для
нахождения более реалистичной оценки переходят к
статистическому суммированию погрешностей аргументов.
Полагая, что в заданных границах погрешности аргументов
распределены равномерно, доверительные границы ΔА(Р)
погрешности результата измерения рассчитывают по
формуле
А( Р ) k
m
bi2 xi2
i 1
k = 1,1 при Р = 0,95 и k = 1,4 при Р = 0,99,
зависит от числа составляющих
неисключенных систематических
погрешностей.
5.
11Нелинейные косвенные измерения
Такие измерения характеризуются тем, что результаты
измерений аргументов подвергаются функциональным
преобразованиям, что приводит к изменению законов их
распределения.
x2
1 -2
е
2
f( x)
q x2
f (q )
1
5 q
е
-
q
2
При измерениях отказываются от использования
интервальных оценок погрешности результата,
ограничиваясь приближенной верхней оценкой ее границ. В
основе приближенного оценивания погрешности лежит
линеаризация функции А f x1 ,..., xm и дальнейшая
обработка результатов, как при линейных измерениях.
6.
Нелинейные косвенные измеренияПусть измеряемая величина А является функцией от
10
x1 ,..., xm
А f x1 ,..., xm
Для простоты считают, что значения распределены по нормальному
закону, измерения равноточные, погрешности измерения не
коррелированы (если погрешность не вызвана каким-либо общим
фактором, изменяющимся случайным образом, например температурой).
Очевидно, что абсолютные погрешности измеряемой величины
являются функцией погрешности прямых измерений
А F x1 , x2 ,..., xm .
В простейшем случае для одной переменной
A A f x x
А f x
f x
А А f x
x .
x
7.
Нелинейные косвенные измеренияf x
А А f x
x .
x
f x
А
x ;
x
f x x
A
100%
100%
A
x A
A
А f x1 ,..., xm
В общем случае для функции
f
f
f
xm
A
x1
x2 ...
x1
x 2
x m
х
i
Если результаты прямых измерений
определены со средними
квадратическими отклонениями i
, то оценка среднего
квадратического отклонения результата косвенных измерений
2
2
2
f 2
f 2 f 2
xm .
x1
x 2 ...
x1
x2
xm
A
9
8.
Нелинейные косвенные измеренияПри коррелированных погрешностях измерений
m f
2
m f f
2
i
A
i j ri j ,
i 1 xi
i , j 1 x i x j
i j
rij - коэффициент корреляции 1 ri j 1 .
f
Ei
i
x i
m
A E
i 1
2
i
- частная погрешность косвенного
измерения.
Если Е k A / 3 , то ею можно пренебречь.
Это условие называется критерием
ничтожных погрешностей, а сами
погрешности, отвечающие этому условию,
называются ничтожными.
8
9.
Правила оценивания погрешности результатакосвенного измерения
Правило 1.
Погрешности в суммах
и разностях.
А x1 x2
А x1 x 2
Правило 2. Погрешности в произведениях и частных.
А x1 x2 А x1 / x2
А x1 x2
Правило 3. Измеренная величина умножается на точное
число.
А C x
А C x
Правило 4. Возведение в степень.
А = xn
А n x
Правило 5. Погрешность в произвольной функции
одной переменной.
А
dA
x
dx
7
10.
4.7. Обработка результатов совместных измерений 6Совместные измерения – это измерения двух или более
неоднородных физических величин для определения зависимости
между ними
Целью совместных измерений является установление
функциональной зависимости между величинами.
Для отыскания зависимости у =f(x) между переменными х и у
необходимо последовательно устанавливая и измеряя
значения х, одновременно измерять величину у, получив,
таким образом координаты исследуемой зависимости (хi , уi ).
Возникающая задача при выполнении совместных измерений:
1. Аппроксимация зависимости по экспериментальным данным так,
чтобы она наилучшим образом описывала истинную зависимость.
2. Ответ на вопрос действительно ли аппроксимирующая функция
наилучшим образом приближается к искомой зависимости и какой
мерой можно оценить приближение экспериментальной зависимости
к истинной.
11.
4.7. Обработка результатов совместных измеренийПодход к решению подобных задач возможен на основе
применения метода наименьших квадратов. В этом методе
оценки параметров зависимости определяют из условия, что
сумма квадратов отклонений расчетных значений
аппроксимирующей функции от экспериментальных
значений должна быть минимальна.
Результаты измерений должны удовлетворять следующим
условиям, при которых получаются несмещенные оценки
параметров зависимости, имеющие минимальные дисперсии:
- значения аргументов хi известны точно;
- систематические погрешности исключены и результаты
измерений уi содержат лишь случайные погрешности,
которые независимы и имеют одинаковые дисперсии;
- погрешности измерения уi имеют нормальное распределение.
5
12.
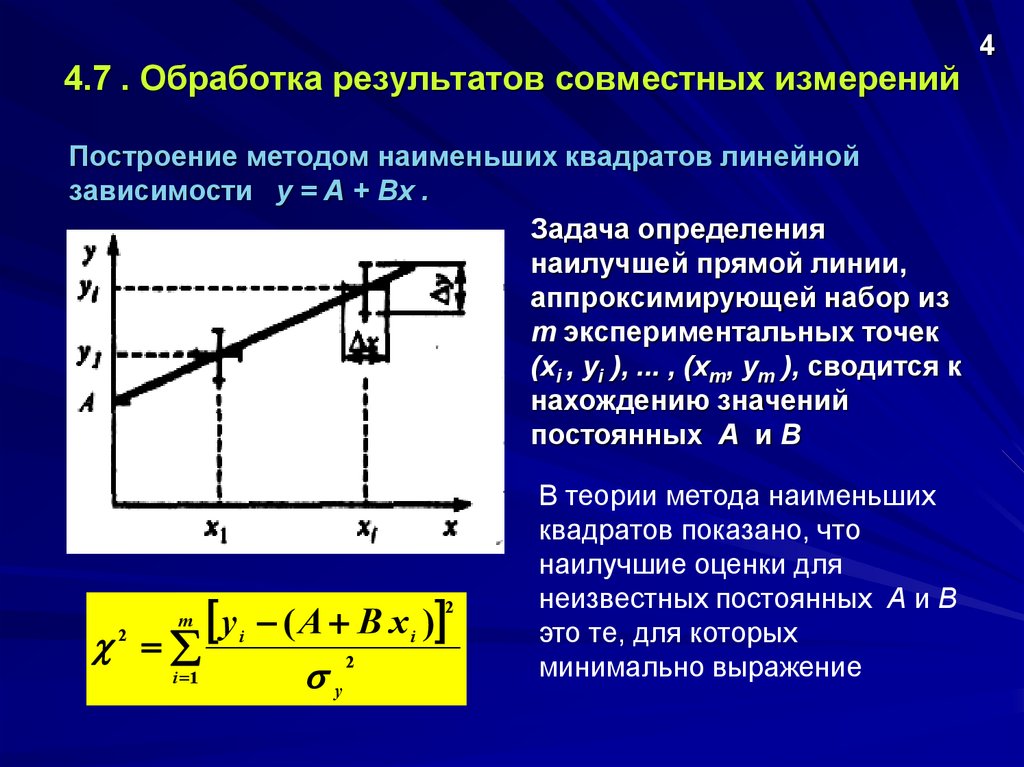
4.7 . Обработка результатов совместных измеренийПостроение методом наименьших квадратов линейной
зависимости у = А + Вх .
Задача определения
наилучшей прямой линии,
аппроксимирующей набор из
т экспериментальных точек
(хi , yi ), ... , (хm, уm ), сводится к
нахождению значений
постоянных А и В
т
у ( A В х )
i 1
у
2
2
i
i
2
В теории метода наименьших
квадратов показано, что
наилучшие оценки для
неизвестных постоянных А и В
это те, для которых
минимально выражение
4
13.
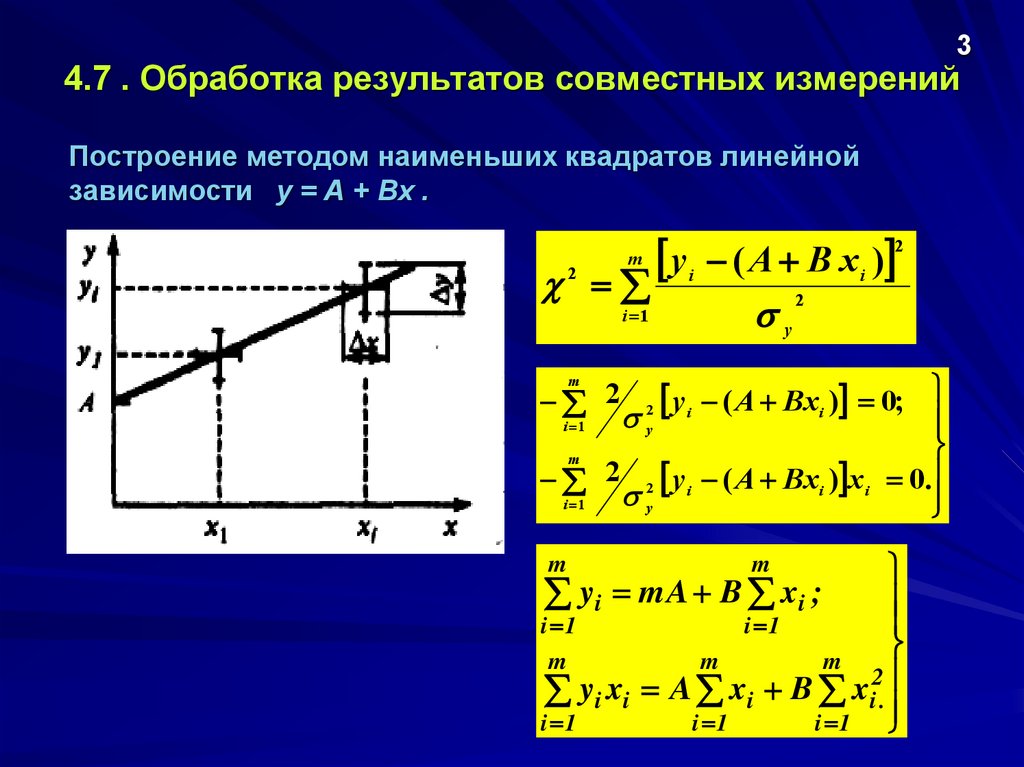
34.7 . Обработка результатов совместных измерений
Построение методом наименьших квадратов линейной
зависимости у = А + Вх .
т
у ( A В х )
i 1
у
2
2
m
2
i
i
2
y ( A Bx ) 0;
2
y
i
i
m
2 2 y i ( A Bx i ) x i 0.
y
i 1
i 1
i 1
i 1
m
m
m
yi xi A xi B xi2.
i 1
i 1
i 1
m
m
yi mA B xi ;
14.
Построение методом наименьших квадратовлинейной зависимости у = А + Вх
m
B
m
m
m yi x i yi x i
i 1
m
i 1
m
2
xi
i 1
2
m
yi
xi
A i 1 B i 1
m
m
xi
i 1
m
m
i 1
Представление о приближении аппроксимирующей функции к
истинной зависимости получим, оценив погрешности в определении
постоянных А и В, которые определяются расчетом по правилам
косвенных измерений, исходя из погрешностей измерения Δy1 , … ,
Δуm.
СКО погрешности измерения σу
может быть известно до начала
m
1
2 измерений, либо вычислено по
2у
yi A Bxi
результатам измерения
m 2 i 1
m
А2 у2 x i2 G
i 1
2
G m xi xi
i 1
i 1
m
B2 m y2 G
m
2
2
15.
Установление зависимости сопротивленияметаллического проводника от температуры
Rt R0 1 t
Rt A B t
1
А = R0; В = R0α.
Результаты совместных измерений:
t 0,С
… … . 10
20
30
40
Rt , Ом … … 10,3
10,9
11,3
11,6
4
B
4
4
4 yi x i yi x i
i 1
4
4
i 1
i 1
2
xi
i 1
2
xi
i 1
4
4
A
yi
i 1
А = 9,95 Ом; В = 0,043 Ом/град
σRt = 0,2 Ом – из пасп. данных
σA =0,24 Ом; σB = 0,009 Ом/град
4
4
B
xi
i 1
y = Rt
x=t
4
А = (9,95 ± 0,24) Ом;
В = (0,043 ± 0,009) Ом/град.
16.
Проверка усвоения материала лекции 7ЗАДАНИЕ № 1 ( выберите один вариант ответа)
Электрическая мощность Р определяется по результатам
измерений падения напряжения U = 240 ± 3 В и силы тока
I = 5 ± 0,1 А, Р = UI. Погрешности измерений носят
систематический характер. Предельные границы истинного
значения мощности равны …
ВАРИАНТЫ ОТВЕТОВ:
1
2
3
4
1191 Вт
1161 Вт
1190,7 Вт
1161,3 Вт
≤ Р ≤ 1209 Вт
≤ Р ≤ 1239 Вт
≤ Р ≤ 1208,7 Вт
≤ Р ≤ 1190,7 Вт
17.
Проверка усвоения материала лекции 7ЗАДАНИЕ № 2 ( выберите один вариант ответа)
Электрическая мощность Р определяется по результатам
измерений падения напряжения U = 220 В и силы тока I = 5 А,
Р = UI. Средние квадратичные отклонения показаний:
вольтметра σU = 1 В, амперметра σI = 0,04 А . Результат
измерения мощности с вероятностью Р = 0,9944 (tp = 2,77)
можно записать …
ВАРИАНТЫ ОТВЕТОВ:
1 P = 1100 ± 14 Вт,
2 P = 1100 ± 0,1 Вт,
3 P = 1100 ± 28 Вт,
4 P = 1100 ± 38 Вт ,
Р = 0,9944
Р = 0,9944
Р = 0,9944
tp = 2,77
18.
Проверка усвоения материала лекции 7ЗАДАНИЕ № 3 ( выберите один вариант ответа)
Коэффициент трения определяется по формуле kтр = Fтр/FN
Измерением получены значения Fтр = 50 ± 0,5H, FN = 1000 ± 10 Н.
Результат определения kтр следует записать …
ВАРИАНТЫ ОТВЕТОВ:
1
2
3
4
kтр = (50,00 ± 0,05) * 10-3
kтр = (50,0 ± 0,5 кг) * 10-3
kтр = 51 * 10-3
kтр = (50 ± 1) * 10-3















 Математика
Математика








