Ražošana un izmaksas
1. Ražošana un izmaksas
2.
Tehnoloģisko sakarību starp ražošanas resursu(faktoru) izmantošanas struktūru un maksimāli
iespējamo produkcijas izlaidi izsaka ražošanas
funkcija.
Ražošanas funkcijas matemātiskā izteiksme:
Q = f (L, K, t, utt.), kur
Q – ražošanas apjoms,
L – darba apjoms,
K – kapitāla apjoms,
t – tehniskais progress,
utt. – pārējie faktori.
Tātad ražošanas apjoms ir izlietoto ražošanas
faktoru funkcija.
3.
Katrs uzņēmējs ir izvēles priekšā - kāduražošanas faktoru kombināciju izvēlēties?
Protams, tādu, kad produkcijas maksimums
tiek nodrošināts pie vismazākā resursu
patēriņa.
Konkretizējot šo vienkāršoto pieņēmumu,
apskatīsim ražošanas faktoru kombināciju
sakarības īsā (short run) un ilgā (long run)
laika periodā, īsā laika periodā vismaz
viens ražošanas faktors ir nemainīgs, bet
ilgā periodā mainās visi ražošanas faktori.
4. Ražošanas funkcija ar vienu mainīgu ražošanas faktoru
Šajā gadījumā visi faktori, izņemot vienu (darba), ir nemainīgi.Ražošanas funkcijas matemātiskā izteiksme ir šāda:
Q = f (L, K, t, etc) = f (L), kur
K, t, etc - nemainīgi lielumi.
Galvenais jautājums - kā darba faktora (L) izmaiņas ietekmēs
kopējo ražošanas apjomu. Lai to noskaidrotu, nepieciešams zināt
un izprast jēdzienus kopējais produkts (total product), vidējais
produkts (average product) un robežprodukts (marginal product).
Kopējais produkts (TP) ir produkcijas apjoms, kas iegūts, izlietojot
noteiktu mainīgā faktora daudzumu.
Vidējais produkts (AP) ir kopējais produkts uz izlietotā mainīgā
faktora vienību. Ekonomikā šo attiecību sauc par darba
ražīgumu.
Robežprodukts (MP) ir kopējā produkta pieaugums (TPn – TPn-1),
kas iegūts mainīgā faktora pieauguma (Ln – Ln-1) dēļ.
5. Ražošanas rezultāti ar vienu mainīgu faktoru
Darbafaktors,
vienības
Kopējais produkts
(TP), vienības
0
1
2
3
4
5
6
7
8
9
0
10
25
38
49
57
62
63
61
58
Darba
robežprodukts
MP = TPn – TPn-1 / Ln
– Ln-1
Vidējais produkts
AP = TP / L
10
15
13
11
8
5
1
-2
-3
10,0
12,5
12,7
12,3
11,4
10,3
9,0
7,6
6,4
6.
Pirmkārt, kopējais produkts pieaug līdz 7.darba vienībasizmantošanai. Sākot ar 8. strādājošo, kopējais produkts
samazinās. Tas liecina, ka šīs darba vienības
izmantošana ir nelietderīga.
Otrkārt, arī vidējais produkts sākumā palielinās, bet, sākot
ar 4.darba vienības izmantošanu, tas krītas.
Treškārt, ļoti svarīga un zīmīga ir robežprodukta dinamika.
Skaidri ir saskatāma robežprodukta saistība ar kopējā un
vidējā produkta dinamiku. Tieši tad, kad robežprodukts
kļūst negatīvs, arī kopējais produkts samazinās.
Robežprodukta dinamika liecina, ka robežprodukts ir
pakļauts krītošam robežražības likumam. Sākot ar 3.
darba vienību, robežprodukts ar katru nākamo darba
faktora pieaugumu samazinās.
Robežražīguma samazināšanās likuma koncepcija ir
šāda - palielinoties kāda ražošanas faktora patēriņam
(pārējiem nemainoties), ražošanas apjoma dinamika
nonāks līdz robežai, kad papildus faktora izmantošana
relatīvi vai pat absolūti samazinās produkcijas izlaides
pieaugumu.
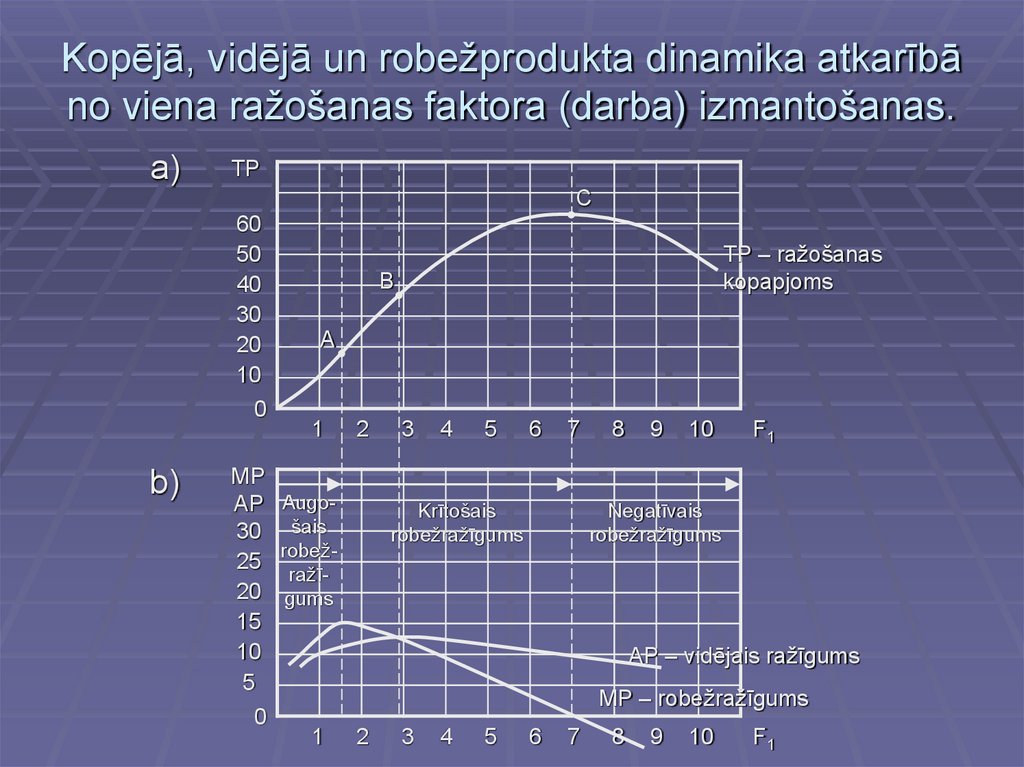
7. Kopējā, vidējā un robežprodukta dinamika atkarībā no viena ražošanas faktora (darba) izmantošanas.
a)TP
C
60
50
40
30
20
10
0
b)
B
A
1
2
MP
AP Augo30 šais
robež25
ražī20 gums
15
10
5
0
TP – ražošanas
kopapjoms
1
3
4
5
6
7
Krītošais
robežražīgums
8
9
10
F1
Negatīvais
robežražīgums
AP – vidējais ražīgums
MP – robežražīgums
2
3
4
5
6
7
8
9
10
F1
8.
Līdz punktam A ražošanas apjoma līkne ir izliekta uz augšu, kasliecina, ka ražošanas apjoms palielinās straujāk nekā faktora L
izmantošana (augošs robežražīgums).
Sākot ar punktu A stāvoklis mainās, un ražošanas apjoma līkne ir
izliekta uz leju. Tas nozīmē, ka produkcijas izlaide notiek lēnāk nekā
faktora L pieaugums. Kopējā produkta pieauguma temps krītas.
Zīmīgi, ka, sākot ar punktu A, robežprodukts samazinās un sāk
darboties krītošais robežražīguma likums.
Arī vidējais produkts turpina palielināties līdz punktam B. Šajā punktā
izveidojas līdzsvars starp vidējo produktu un robežproduktu. MP un
AP līkņu krustpunktā AP līkne sasniedz maksimumu un pēc tam,
samazinoties robežproduktam (MP), arī vidējais produkts (AP)
samazinās. Robežprodukta un vidējā produkta samazināšanās
izraisa vēl lielāku kopējā produkta (TP) pieauguma tempu
samazināšanos.
Beidzot nonākam punktā C, kopējais produkts sasniedz savu
maksimumu, bet MP = 0. Kad robežprodukts (MP) kļūst negatīvs, arī
kopējais produkts (TP) absolūti samazinās.
Robežprodukts ir tas faktors, kas ietekmē gan kopējo, gan arī vidējo
produktu. Krītošā ražīguma likumam ir pakļauta gan kopējā, gan
vidējā produkta dinamika, bet šī procesa noteicošais faktors ir
krītošais robežražīgums.
9. Ražošanas funkcija ar diviem mainīgiem faktoriem
Reālajā saimnieciskajā situācijā mainās ne tikai viensražošanas faktors. Tādējādi nākamais solis racionālas
uzņēmēja rīcības izpētē ir ražošana ar diviem mainīgiem
faktoriem.
Ražotāja izvēle ir saistīta ar savstarpēji aizvietojamu
ražošanas faktoru izvēli, lai ražotu fiksētu produkcijas
apjomu. Viena faktora samazināšanās tiek kompensēta
ar otra faktora palielināšanos, nemainot ražošanas
izlaides apjomu.
Šīs divfaktoru ražošanas funkcijas matemātiskā izteiksme ir:
Q = f (L, K), kur
gan darbs (L), gan arī kapitāls (K) ir mainīgi lielumi.
10.
Divfaktoru ražošanas funkcijas grafiskais attēls irvienādo ražošanas apjomu līkne,
starptautiskajā terminoloģijā – izokvante.
Vienādo apjomu līknes (izokvantes).
Mašīnlaika
stundas
K
6
5
4
3
2
1
0
A
-ΔK
B
ΔL
1
C
2
3
D
4
Q3 = 300
Q2 = 200
Q1 = 100
E
5
6
Darba stundas
7
8
9
L
11.
Vienāda apjoma līkne (izokvante) ir ģeometriskavieta visām tām ražošanas faktoru kombinācijām,
ar kuru palīdzību var sasniegt noteiktu ražošanas
apjomu. Mūsu piemērā pirmajā gadījumā Q ir 100,
otrajā - 200, bet trešajā - 300 vienības. Var novilkt
bezgala daudz vienādo apjomu līkņu, un katra no
tām raksturos noteiktu apjoma līmeni.
Izokvantēm ražošanas faktoru izvēlē ir tāda pati
loma kā vienaldzības līknēm, nosakot patērētāja
priekšrocības. Līdz ar to arī ražotāja līdzsvara
koncepcija metodoloģiski sakrīt ar patērētāja
līdzsvara modeļu variantu.
12.
Uzņēmējs ar izokvantes palīdzību meklēvisracionālāko darba un kapitāla kombināciju,
aizvietojot vienu ar otru. Aizvietošanas iespējas
nosaka gan tehnoloģiskie, gan arī ekonomiskie
nosacījumi.
Pieņemsim, ka atrodamies punktā A. Ražošanas
apjoms tiek sasniegts, izlietojot vienu darba
stundu un sešas mašīnstundas. Tehnoloģiskās
iespējas vēl vairāk samazināt darba patēriņu ir
problemātiskas. Bezcilvēku tehnoloģijas līmeni
mēs neesam sasnieguši, un to atspoguļo
izokvantes slīpuma leņķis, kas arvien vairāk
samazinās, un līkne kļūst vertikāla.
Punktā E stāvoklis ir pretējs. Samazināt kapitāla
izmantošanu tīri tehnoloģiski nav iespējams.
13.
Kurā punktā būs visracionālākā uzņēmēja izvēle?Lai atbildētu uz šo jautājumu, mums jāiepazīstas
ar jēdzienu, kura nosaukums ir tehniskās
aizvietojamības robežnorma, saīsināti MRTS.
Tas ir mērs, kas izsaka, par cik mainītos viena
ražošanas faktora (kapitāla) izlietošana,
mainoties otra faktora (darba) izmantošanai par
vienu vienību.
Konkrētajā piemērā darba aizvietošanas
robežnorma ar kapitālu ir šāda:
-ΔK
MRTSLK=
ΔL , kur
MRTSLK - tehniskās aizvietojamības robežnorma,
∆K - kapitāla pielietojuma izmaiņas,
∆L - darba pielietojuma izmaiņas.
14.
Šis vienādojums nosaka izokvantes konfigurāciju vaislīpuma leņķi. Tomēr neatbildēts paliek jautājums – kādu
noteikumu gadījumā uzņēmējs izvēlēsies vislabāko
darba un kapitāla kombināciju?
Labākā kombinācija būs variants, kad ieguvums no
ražošanas faktoru aizvietošanas ir vienāds ar
zaudējumiem, atsakoties no otra ražošana faktora.
Šā stāvokļa matemātiskā izteiksme:
ΔL x MPL = –ΔK x MPK
Tātad robežprodukts vai robežražīgums atrisina šo
problēmu, faktiski robežprodukts ir tas, kas nosaka
darba un kapitāla aizvietošanas robežas. Līdz ar to var
izvērstākā formā noteikt izokvantes slīpumu vai
tehniskās aizvietojamības robežnormu.
-ΔK
MPL
MRTSKL=
=
ΔL
MPK
15.
Lai uzņēmējs izvēlētos vislabāko ražošanasfaktoru kombināciju, pastāvot noteiktam
ražošanas apjomam, viņam jāzina ražošanas
faktoru cenas.
Izmaksu summu, kas saistīta ar dotā apjoma
ražošanu, sauc par kopējām izmaksām (TC).
Dotajā gadījumā ar divu faktoru kombināciju
kopējās izmaksas var izteikt ar formulu:
TC = PL x QL + PK x QK, kur
TC – kopējās izmaksas,
PL – darba vienības cena,
PK – kapitāla vienības cena,
QL – darba vienību apjoms,
QK – kapitāla vienību apjoms.
16.
Ja pieņemam, ka dotajā brīdī ražošanas faktoru (darba unkapitāla) cenas ir nemainīgas, tad šo vienādojumu var
uzrakstīt par vienādo izmaksu vienādojumu (izokostu).
Vienādo izmaksu taisne izsaka visas iespējamās divu
ražošanas faktoru (QL un QK) kombinācijas, kas atbilst
vienādai izmaksu summai.
Lai ražotājs būtu līdzsvarā, tad vai nu viņam ir jāmaksimizē
produkcijas izlaide kopējo izmaksu ietvaros un
jānodrošina šāda sakarība realizācijā:
Q = f (L, K) = maks.
TC = PL x QL + PK x QK = konst.
vai arī jāiegūst dotais ražošanas apjoms ar minimālām
ražošanas izmaksām:
Q = f (L, K) = konst.
TC = PL x QL + PK x QK = min.
17.
Tātad ražotāja līdzsvars vai uzņēmējavisracionālākā ražošanas faktoru izvēle būs tad,
kad produkcijas maksimums tiks nodrošināts ar
vismazāko resursu patēriņu.
Praktiski ražošanas faktoru aizvietošana izmaksu
minimizācijas virzienā turpināsies līdz tam
laikam, kamēr atsevišķu ražošanas faktoru
robežražīgums, ko izsaka šo faktoru
robežprodukts, nebūs proporcionāls šo faktoru
cenām.
Tādējādi ražotāja līdzsvaru var izteikt ar izteiksmi:
MPL
=
MPK
=
MPn
PL
PK
Pn , kur
MP – darba, kapitāla un citu resursu robežprodukts,
P – darba, kapitāla un citu resursu cenas.
18.
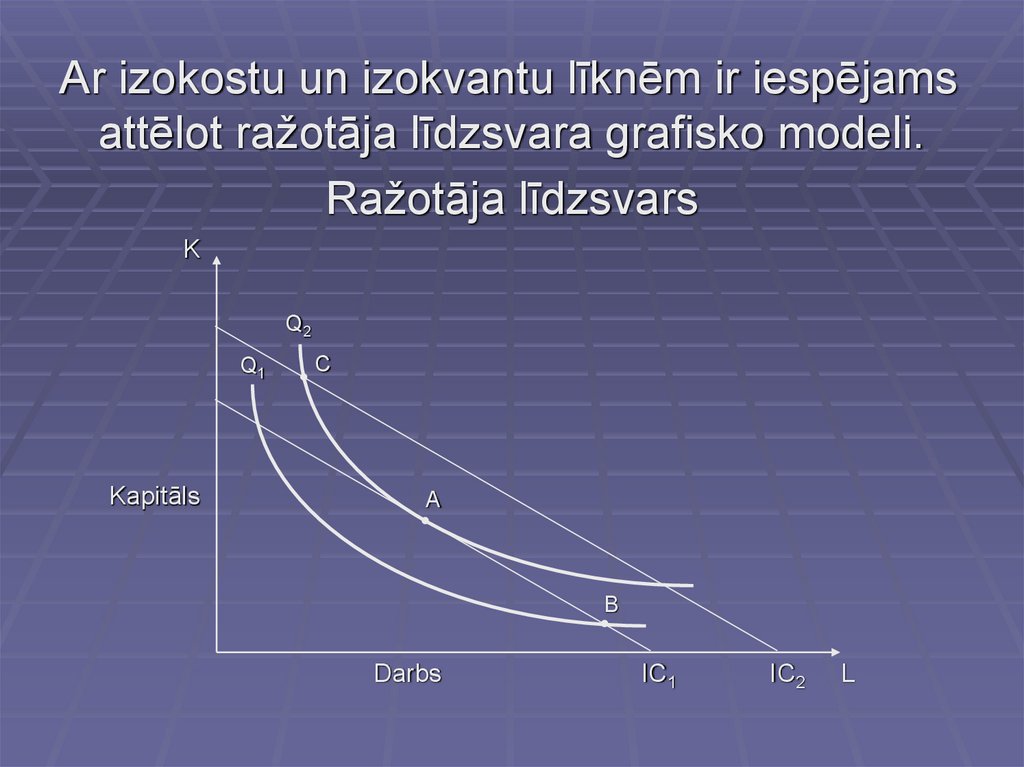
Ar izokostu un izokvantu līknēm ir iespējamsattēlot ražotāja līdzsvara grafisko modeli.
Ražotāja līdzsvars
K
Q2
Q1
Kapitāls
C
A
B
Darbs
IC1
IC2
L
19.
Ražotajā līdzsvara punkts ir A, šajā punktā uzņēmējsminimizēs izmaksas pie dotā ražošanas apjoma Q2.
Tieši šajā punktā – vienādo izmaksu un vienādo
ražošanas apjomu līkņu pieskares punktā – sakrīt
vienādo izmaksu taisnes un vienādā apjoma līknes
slīpums.
Tā kā vienādo izmaksu taisnes slīpumu nosaka darba un
kapitāla vienības cenu attiecības, bet vienādo apjomu
līknes slīpumu nosaka tehniskās aizvietojamības norma,
tad A punktā:
MPL
PL
= MRTSKL =
MPK
PK
Neviens cits punkts neatbilst ražotāja līdzsvara
noteikumiem. Punkts C nav pieņemams, jo tas atrodas
uz augstāku izmaksu līknes IC2 bet punkts B atspoguļo
zemāku ražošanas līmeni Q1.
20. Īslaicīgās ražošanas izmaksas
Ražošanas izmaksas ir uzņēmēja izdevumu kopums, kasnepieciešams, lai ražotu noteiktu preču un pakalpojumu
apjomu. Visu izmaksu summu, kas saistīta ar dotā
produkcijas apjoma ražošanu sauc par kopējām
izmaksām (total cost TC).
Izmaksas īsā laika periodā klasificē kā pastāvīgās (fixed
cost - FC) un mainīgās (variable cost - VC). Izmaksas,
kuru lielums nav atkarīgs no ražojamās produkcijas
apjoma, ir pastāvīgās izmaksas, bet izmaksas, kuru
lielums mainās atkarībā no ražošanas apjoma, ir
mainīgās izmaksas.
Šāds iedalījums attiecas tikai uz īso laika periodu – kurā
nemainās kāds no ražošanas faktoriem (parasti kapitāla
izmaksu elementi – iekārtas, ēkas).
Ilglaicīgā periodā mainās visi ražošanas faktori.
21. Izmaksas augstskolā (piemērs)
TCIzmaksas
VC
TVC
Mācību personāla
darba alga
Administrācija
Telpu uzturēšana
Apsardze
Apkure
Amortizācija
Telpas
FC
q1
q2
q
Kopējās izmaksas (TC) ir kopējo pastāvīgo (TFC) un kopējo
mainīgo (TVC) izmaksu summa:
TC = TFC + TVC, kur
TFC – konstants,
TVC – f(Q), kur Q ir ražošanas apjoms.
Ja kopējās mainīgās izmaksas (TVC) ir ražošanas apjoma funkcija,
tad arī kopējās izmaksas (TC) ir ražošanas apjoma funkcija TC =
f(Q), jo TFC ir fiksēts lielums.
22.
Kāda nozīme ir kopējām izmaksām?Pirmkārt, tas apstāklis, ka TC = f(Q), noteic, ka kopējās izmaksas var
minimizēt tikai tad, ja ir noteikts ražošanas apjoms. Tātad kopējās
izmaksas ir viens no ražošanas apjoma optimizēšanas faktoriem.
Otrkārt, uzņēmējam vienmēr ir jāsalīdzina kopējās izmaksas (TC) un
kopējie ienākumi (total revenue - TR). Ja TC > TR, tad firma atrodas
zaudējumu zonā, bet ja TC < TR, tad firmai ir ienākumi. Pie TC un TR
līdzsvara firma atrodas uz bezzaudējuma punkta.
Vidējās izmaksas (average cost - AC) ir izmaksas, rēķinot uz vienu
produkcijas vienību. Mēs izšķiram vidējas kopējās izmaksas (average
total cost - ATC), vidējās fiksētās izmaksas (average fixed cost - AFC)
un vidējās mainīgās izmaksas (average variable cost -AVC).
Vidējās izmaksas aprēķina, dalot kopējās izmaksas ar produkcijas
apjomu Q.
ATC =
TC
Q
=
TC
Q
TFC
Q
; AFC =
+
TVC
Q
ATC = AFC + AVC
TFC
Q
; AVC =
TVC
Q
;
23.
Vidējas izmaksas kā izmaksas uz vienu ražošanas vienībuizmanto teorijā un praksē, salīdzinot tās ar realizācijas
cenu. Sevišķi liela nozīme ir vidējām mainīgām
izmaksām (AVC).
Ja realizācijas cena ir zemāka par AVC, tad uzņēmēja
stāvoklis ir bezcerīgs.
Ja cena pārsniedz vidējās mainīgās izmaksas, bet
nekompensē vidējās fiksētās izmaksas (AFC), tad
stāvoklis nav labs, tomēr ar attiecīgā biznesa slēgšanu
nedrīkstētu steigties, jo AFC ir ieguldītas noteiktajā
ražotnē un, slēdzot uzņēmumu, vislabākajā gadījumā
izdosies atgūt tikai daļu no šīm izmaksām. Bezgalīgi
šāds stāvoklis nevar turpināties, uzņēmējam jāmeklē ceļi
izmaksu samazināšanai.
Vidējās mainīgās izmaksas var salīdzināt ar dzīvības līniju ja vidējās mainīgās izmaksas ir zemākas par cenu, tad
biznesam ir cerības izdzīvot, bet ja tās pārsniedz cenu,
tad cerību vairs nav.
24.
Vissvarīgākā izmaksu grupa – robežimaksas (marginal cost - MC).Robežizmaksas ir kopējo izmaksu pieaugums, palielinot ražošanas apjomu
par vienu vienību. Tās ir pēdējās ražotās vienības izmaksas:
ΔTC
MC =
ΔQ
Tā kā pastāvīgās izmaksas (TFC) nav atkarīgas no ražošanas apjoma, tad
robežizmaksas kā papildus produkcijas vienības izmaksas ir atkarīgas tikai
no kopējām mainīgām izmaksām.
ΔTVC
MC =
ΔQ
Tātad MC = f(TVC), tas ir, robežizmaksas ir kopējo mainīgo izmaksu funkcija.
Robežizmaksām ir noteicošā nozīme ražošanas apjoma optimizācijā. Tās
nosaka robežlīniju, aiz kuras ražošanas paplašināšana nes zaudējumus.
Šo robežu nosaka robežizmaksu un tirgus cenas vienlīdzība (MC = P). Ja vēl
vienas ražotās vienības izmaksas pārsniedz attiecīgās preces cenu, tad
firmai zaudējumi ir neizbēgami.
Robežizmaksām ir stratēģiska nozīme. Tās parāda, cik firmai maksā pēdējās
vienības ražošana, un vienlaikus parāda to ieguvumu, ko iespējams gūt,
atsakoties no šīs vienības ražošanas.
Tātad robežizmaksas sniedz informāciju par ražošanas izmaksu izmaiņām
ražošanas apjoma paplašināšanās vai sašaurināšanās gadījumos. Vidējās
izmaksas šādu informāciju nedod. Robežizmaksu nozīme gan cenu
formēšanā, gan ražošanas apjoma optimizācijā, gan arī peļņas
maksimizācijas procesos nav apstrīdama.
25. Kopējo izmaksu, vidējo un robežizmaksu grafiska analīze
Kopējāsizmaksas
TC
TVC
60
40
TFC
20
0
2
4
6
8
Vidējās
un robežizmaksas
10
12
Ražošanas apjoms
MC
40
ATC
30
20
AVC
10
AFC
0
2
4
6
8
10
12
Ražošanas apjoms
26.
Sakarības, ko izsaka kopējo izmaksu grafiskais modelis:1) Kopējo izmaksu (TC) dinamiku nosaka kopējās mainīgās
izmaksas (TVC), jo kopējās fiksētās izmaksas (TFC) īsā
periodā ir nemainīgas. Tādējādi TC un TVC līkņu
konfigurācija ir identiska;
2) TC un TVC līknēm ir S veida konfigurācija. Sākumā
kopējās izmaksas ir augstas, jo fiksētās izmaksas
ražošanā ir vērā ņemams faktors, tās eksistē pat tad, kad
nenotiek ražošana. Vidus posmā ražošanas apjoms
pieaug straujāk nekā izmaksas (mainīgā faktora pieaugošā
ražība). Šinī posmā uzņēmējs gūst ļoti labus ieņēmumus.
Beigu posmā TVC līkne ir krasi izliekta uz augšu. Šeit ar
pilnu spēku darbojas krītošais ražīguma likums;
3) Treškārt - faktiski TVC pieauguma dinamiku nosaka
robežizmaksu (MC) pieaugums. Kopējo mainīgo izmaksu
līknes slīpums ir atkarīgs no tā, kā mainās robežizmaksas,
mainoties ražošanas apjomam.
27.
Sakarības, ko izsaka vidējo un robežizmaksu grafiskaismodelis:
1) Vidējo kopējo izmaksu (ATC) un vidējo mainīgo izmaksu
(AVC) līknēm ir U veida konfigurācija (var būt deformēta U
veida līkne). Arī vidējās izmaksas sākotnēji ir augstas. To
cēlonis ir nelieli ražošanas apjomi un fiksēto izmaksu
esamība. Iespaidīgais vidējo izmaksu kritums ir saistīts tieši
ar pastāvīgo izmaksu (FC) ekonomiju, pieaugot ražošanas
apjomam.
Vidējo kopējo izmaksu pieaugums ir saistīts ar vidējo mainīgo
izmaksu (AVC) pieaugumu, ko nespēj amortizēt vidējo
pastāvīgo izmaksu (AFC) samazinājums, jo tas, pieaugot
ražošanas apjomam, samazinās. Vidējās mainīgās
izmaksas (AVC) sasniedz minimumu pie 6 ražošanas
vienībām, turpretim vidējās kopējās izmaksas (ATC)
minimumu sasniedz, ja ražošanas apjoma ir lielāks (8
vienības). Tas notiek tāpēc, ka ATC ietekmē gan AVC, gan
AFC, un tikai tad, kad vidējo fiksēto izmaksu samazinājums
nekompensē vidējo mainīgo izmaksu pieaugumu, tad arī
vidējās kopējās izmaksas sāk pieaugt.
28.
2) Aplūkojot robežizmaksu (MC) un vidējomainīgo izmaksu (AVC) mijiedarbību, redzams,
ka tās sākotnēji iziet no viena punkta. Tas tāpēc,
ka pirmās vienības AVC = MC. Robežizmaksas
samazinās straujāk un savu minimumu sasniedz
pie mazāka produkcijas apjoma nekā vidējās
kopējas un vidējās mainīgās izmaksas. Augošās
robežizmaksas šķērso vidējās mainīgās (AVC)
un kopējās vidējās izmaksas (ATC) šo izmaksu
minimuma punktā.
Tas nozīmē, ka tad, ja robežizmaksu lielums
zemāks par vidējām izmaksām, vidējo izmaksu
līkne ies lejup, bet, ja robežizmaksu lielums
augstāks par vidējām izmaksām, vidējo izmaksu
līkne ies augšup. Tas, savukārt, noteic, ka
robežizmaksu līkne krusto AVC un ATC šo līkņu
minimuma punktā.
29. Ražošanas izmaksas ilglaicīgā periodā
Ja uzņēmums tiek modernizēts, ieviešotjaunas iekārtas un tehnoloģijas - visas
izmaksas ir mainīgas un tas raksturo
izmaksas ilgā laika periodā (long run).
Ilgais laika periods nav kalendārais laiks,
tas ir saistīts ar visu ražošanas faktoru
izmaiņām.
30.
Katram uzņēmuma lielumam atbilst savas īslaicīgāsvidējo izmaksu līknes (SATC).
Izmaksas
SATC
LATC
SATC2
SATC1
SATC3
A
C
LATC
B
Q1
Q2
Q3
Ražošanas apjoms Q
SATC1 atbilst nelielam uzņēmumam, SATC2 –
vidējam, bet SATC3 – lielam uzņēmumam.
31.
Savienojot īsā laika perioda vidējo izmaksu līknesar pieskares līkni, iegūst ilgā laika perioda
izmaksu līkni (LATC). Aplūkojot garā perioda
vidējo izmaksu līkni, redzam, ka, palielinoties
uzņēmuma lielumam, vidējās izmaksas
samazinās, sasniedz minimumu, pēc tam
pieaug.
Šādu līknes raksturu nosaka apjoma efekts. Līdz
minimuma punkta sasniegšanai tas ir pozitīvs
(līknes lejupslīdošā daļa), bet pēc tam negatīvs
(līknes kāpjošā daļa). Ilgā laika perioda vidējās
izmaksas ļauj izvēlēties visoptimālākos
uzņēmuma apmērus.
32.
Apjoma pozitīvais un negatīvais efekts ir viens nosvarīgākajiem nozares struktūru noteicošajiem
faktoriem. Tas nosaka nozarē darbojošos
uzņēmumu lielumu un skaitu. Zinām, ka ir
nozares, kurās darbojas liels firmu skaits, bet ir
tādas ražošanas nozares, kur ir tikai dažas vai
pat viena firma. Tam par iemeslu ir vairāki
faktori, tomēr apjoma efektam ir ārkārtīgi liela
nozīme.
Šai sakarā var runāt par uzņēmuma minimālo
efektīvo lielumu. Tas ir mazākais ražošanas
apjoms, kuru ražojot firma var minimizēt savas
garā perioda vidējās izmaksas.
33.
ALAC
LAC
0
LAC
Q1
Q2
Q
B
LAC
0
LAC
Q
C
LAC
0
Q
34.
A gadījumā garā perioda vidējās izmaksas (LAC) var minimizēt,sākot ar ražošanas apjomu Q1. Vidējās izmaksas paliek
nemainīgas līdz ražošanas apjomam Q2. Tas nozīmē, ka
intervālā Q1 - Q2 visas firmas ir vienādi efektīvas. Tāpēc šajā
nozarē var sekmīgi darboties dažāda lieluma firmas. Tādas ir
mēbeļu ražošanas, kokapstrādes un dažas citas nozares.
B gadījumā ir attēlota nozare, kurā pozitīvais apjoma efekts ir
ilgstošs, bet negatīvais efekts iestājas, ja ražošanas apjomi ir ļoti
lieli. Tāds stāvoklis ir automobiļu, alumīnija, metalurģijas un
daudzās citās smagās rūpniecības nozarēs. Tas nozīmē, ka dotā
pieprasījuma apjoma ietvaros pietiekošu ražošanas efektivitāti
var sasniegt tikai daži lieli uzņēmumi. Var izveidoties situācija,
kad nozarē efektīvo ražošanas apjomu sasniedz tikai viena firma.
Nozarē, kur pozitīvais apjoma efekts ir neliels, bet negatīvais
iestājas ļoti ātri (C gadījumā), uzņēmuma minimālais efektīvais
lielums iestājas, ja ražošanas apjomi ir nelieli. Šādā nozarē doto
pieprasījuma apjomu apmierinās liels relatīvi nelielu uzņēmumu
skaits. Šāda situācija ir raksturīga daudziem mazumtirdzniecības
veidiem, šūšanas, dažām pārtikas rūpniecības, sabiedriskās
ēdināšanas un tamlīdzīgām nozarēm.
35.
Jebkuras firmas stratēģijas un taktikas centrā irienākumu un izmaksu salīdzināšana.
Starpību starp kopējiem ienākumiem (TR - total
revenue) un kopējām izmaksām (TC), ieskaitot
alternatīvās izmaksas (opportunity vai arī implicit
cost), sauc par ekonomisko peļņu (economic
profit). Šīs sakarības matemātiskā izteiksme:
TR – TC = ekonomiskā peļņa.
Ja kopējās izmaksās ieskaitītas tikai
grāmatvedības izmaksas (accounting cost), kas
saistītas ar tiešo saimniecisko darbību, tad:
TR – TC = grāmatvedības peļņa.
36. Realizācijas apjoma - izmaksu - ienākumu grafiskais modelis
Realizācijas apjoma - izmaksu ienākumu grafiskais modelisIzmaksas,
ienākumi
Kopējie ienākumi
Peļņa
Bezzaudējuma
punkts
Zaudējumi
Kopējās izmaksas
Kopējās mainīgās izmaksas
Kopējās fiksētās izmaksas
Ražošanas apjoms
37.
Bezzaudējuma punkts (break - even point) irražošanas (realizācijas) apjoms, kad kopējās
izmaksas ir vienādas ar kopējo ienākumu vai
vidējās izmaksas ir vienādas ar ražotā
(realizētā) produkta cenu.
Bezzaudējuma punkts (BEP) nodrošina īpašu
saikni starp tirgus cenu, izmaksām un ražošanas
(realizācijas) apjomu. Bezzaudējuma punkta
noteikšana ļauj izvēlēties tādas cenas, izmaksu
un ražošanas (realizācijas) apjoma attiecības,
kas firmai nodrošina gan pašatmaksāšanās
principa īstenošanu, gan arī noteiktas peļņas
iegūšanas nosacījumus.
38.
Piemērs.Pieņemsim, ka netālu no pilsētas centra ir pieejamas neizmantotas
telpas pieklājīgā pilsētas mājā. Iecerētā biznesa mērķis ir iekārtot
specializētu alus bāru ar devīzi - vienkārši un kvalitatīvi. Lai ķertos
pie nodoma īstenošanas, nepieciešami daži ekonomiskie aprēķini.
Pirmkārt, būtu jātiek skaidrībā ar kopējām fiksētām izmaksām (TFC).
Nepieciešams telpu remonts, iekārtojums, būs airī administratīvie
izdevumi. Aprēķini liecina, ka TFC būs EUR 45 000. Kredītnoteikumi
paredz šo summu segt triju gadu laikā, tātad viena perioda kopējās
fiksētās izmaksas būs EUR 15 000.
Otrkārt, nepieciešams apsvērt, kāda būs viena kausa alus pārdošanas
cena un vidējās mainīgās izmaksas (AVC) uz vienu kausu alus.
Nosakot AVC, galvenokārt jānoskaidro, par kādu cenu būs jāiepērk
alus. Pieņemsim, ka prognozējamā kausa alus pārdošanas cena
būs EUR 1,50, bet vidējās mainīgās izmaksas – EUR 0,50.
Atņemot no pārdošanas cenas vidējās mainīgās izmaksas, iegūsim
tā saukto fiksēto izmaksu segumu – maržu – uz vienu vienību.
P – AVC = marža, kur
P – pārdošanas cena
AVC – vidējās mainīgās izmaksas
Marža – segums uz 1 vienību.
39.
Nepieciešamo realizācijas apjomu, kas nodrošinaalus bāram bezzaudējuma stāvokli, var noteikt
pēc formulas:
TFC
BEP =
marža
, kur
BEP – bezzaudējuma punkts;
TFC – kopējās fiksētās izmaksas;
marža – segums uz vienu vienību.
Kādam jābūt realizācijas apjomam, lai minētais
alus bārs pirmajā darbības gadā nodrošinātu
bezzaudējuma stāvokli?
BEP =
EUR 15000
EUR 1,5 – EUR 0,50
= 15000 vien.
40.
Firmas darbības izvērtēšanu nosaka ar kopējo maržu.TR – TVC = TM, kur
TR – kopējie ienākumi;
TVC – kopējās mainīgās izmaksas;
TM – kopējā marža.
Firmas darbības turpināšanas priekšnoteikums ir TR – TVC > 0
pat tad, kad firma īsā laika periodā strādā ar zaudējumiem
un nekompensē fiksētās izmaksas. Firmas tūlītējas
slēgšanas gadījumā zaudējumi būtu vēl lielāki, jo fiksētās
izmaksas eksistē arī tad, kad ražošana tiek pārtraukta. Ilgu
laiku šāds stāvoklis nevar pastāvēt, tāpēc jāmeklē ceļi, kā
uzlabot firmas darbību.
Ja firmai TR – TVC = TM = TFC, tad firma atrodas
bezzaudējuma stāvoklī, jo kopējais segums kompensē gan
kopējās mainīgās, gan arī kopējās fiksētās izmaksas.
Firma gūst peļņu tad, kad TR – TVC = TFC + peļņa. Kopējā
marža šeit nodrošina gan visu izmaksu kompensāciju, gan
peļņas iegūšanu.






































 Лингвистика
Лингвистика