Теория графов. Обыкновенные графы

1.

Теория графов
Обыкновенные графы
Костюк Ю.Л.
доктор технических наук, профессор

2.

Элементы теории графов
Граф G = {V, E} - два множества V и E.
V – множество вершин (узлов) графа, |V | = n
E – множество рёбер графа, |E | = m
Ребро в обыкновенных графах – пара вершин: (i, j)
ребро соединяет i и j, i ≠ j, порядок не важен, вершины i и j смежные, обе
вершины инцидентны ребру, ребро инцидентно вершинам
Степень (валентность) вершины – число инцидентных рёбер

3.

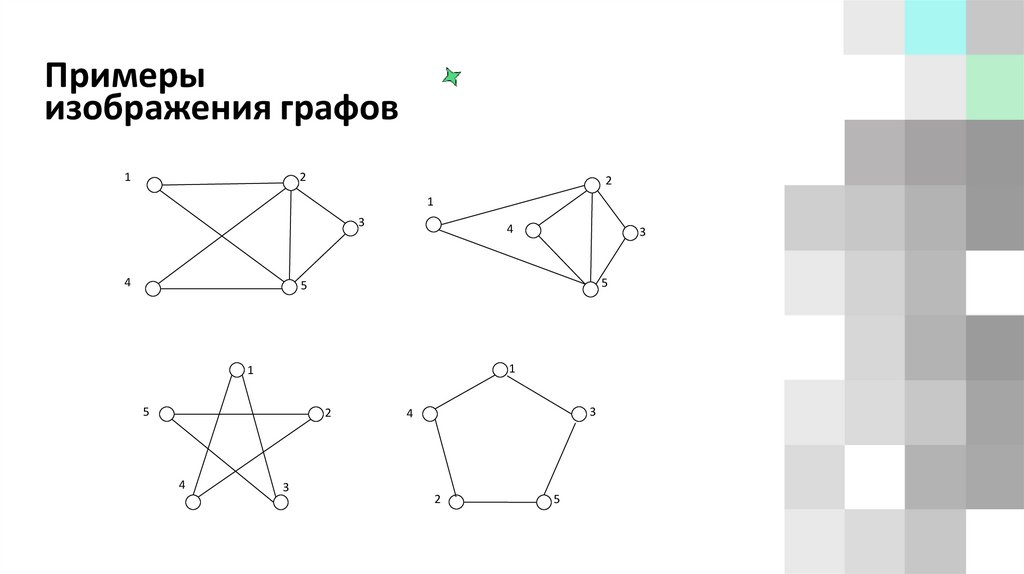
Примеры
изображения графов
1
2
2
1
3
4
4
3
5
5
1
1
5
2
4
3
3
4
2
5

4.

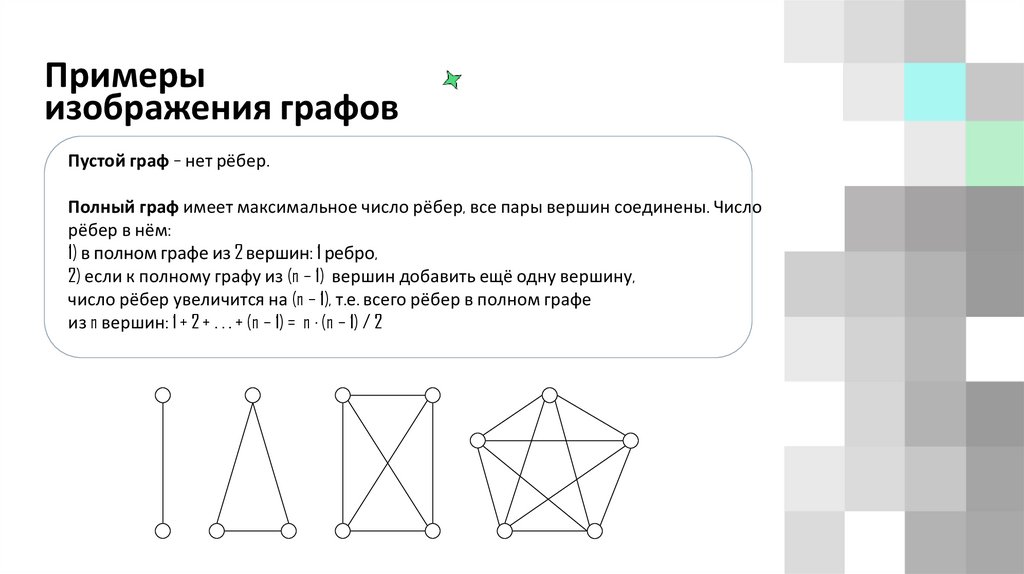
Примеры
изображения графов
Пустой граф – нет рёбер.
Полный граф имеет максимальное число рёбер, все пары вершин соединены. Число
рёбер в нём:
1) в полном графе из 2 вершин: 1 ребро,
2) если к полному графу из (n – 1) вершин добавить ещё одну вершину,
число рёбер увеличится на (n – 1), т.е. всего рёбер в полном графе
из n вершин: 1 + 2 + . . . + (n – 1) = n ∙ (n – 1) / 2

5.

Граф – математическая модель для реальных объектов
А
В
Вершина В достижима из вершины А, если можно из
А по рёбрам и промежуточным вершинам добраться до В,
т.е. есть путь из А в В.
Простой путь не содержит более одного раза одну
и ту же вершину. Простых путей может быть более одного,
тогда требуется найти самый кратчайший путь с наименьшим числом
промежуточных вершин.
Решение этой задачи:
1) вычисление кратчайших расстояний от начальной
вершины до всех остальных;
2) отслеживание пути (в обратном порядке) от конечной
вершины до начальной.

6.

Алгоритм 1.
Просмотр графа вширь
Входные данные: граф, начальная вершина А
1
Создаётся очередь, в её начало записывается А. Вершине А записывается
расстояние 0 от начальной вершины. Для вершины А записывается ссылка
0. Вершина А становится текущей.
2
Вершинам, смежным с текущей, записываются расстояния,
на 1 больше, чем у текущей. Смежные вершины помещаются
в очередь (если там их раньше не было). Всем этим вершинам
записывается ссылка на текущую вершину (на её номер
в очереди).
3
Текущей становится следующая в очереди вершина,
если она есть, и повторяется шаг 2.

7.

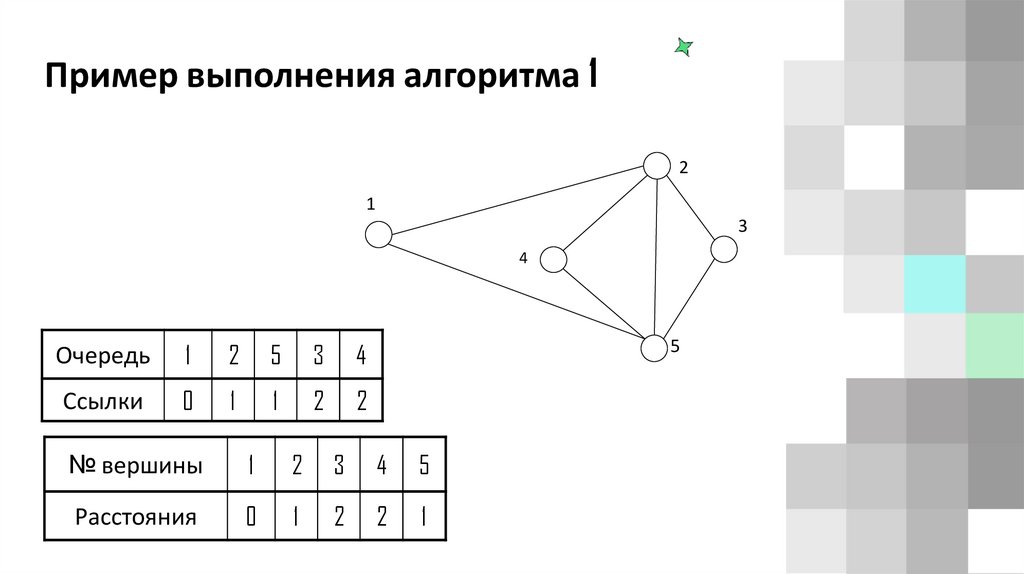
Пример выполнения алгоритма 1
2
1
3
4
Очередь
1
2
5
3
4
Ссылки
0
1
1
2
2
5
№ вершины
1
2
3
4
5
Расстояния
0
1
2
2
1

8.

Алгоритм 2.
Отслеживание пути
Входные данные: результат работы алгоритма 1,
конечная вершина В
1
2
3
В очереди ищется и находится конечная вершина В,
и она становится текущей
Текущая вершина записывается в путь в обратном порядке
Если у текущей вершины ссылка не нулевая, то текущей становится
вершина по ссылке и повторяется шаг 2
Алгоритм 2 отслеживает только один из самых коротких путей, если
их несколько.

9.

Связность графа
Если в графе любая пара вершин взаимно достижимы, то
такой граф связный.
Граф может быть несвязным, тогда связные подмножества
вершин и рёбер между ними образуют подграфы —
компоненты связности.
Например, для графа, представляющего города и дороги,
компоненты связности это такие группы городов, что города
в каждой группе соединены между собой дорогами,
а между группами дорог нет.

10.

Алгоритм 3. Разделение графа
на компоненты связности
Входные данные: граф
1 Вершина 1 становится текущей. Номер текущей компоненты = 0.
Если у текущей вершины нет метки, то:
2 номер текущей компоненты увеличивается на 1,
иначе переход к шагу 5.
3
Выполняется алгоритм 1, текущая вершина — начальная для просмотра.
4
Просматривается очередь, полученная алгоритмом 1,
всем вершинам в очереди записывается метка, равная номеру текущей
компоненты
5
Текущей становится вершина со следующим номером
(если она есть), и повторяется шаг 2

11.

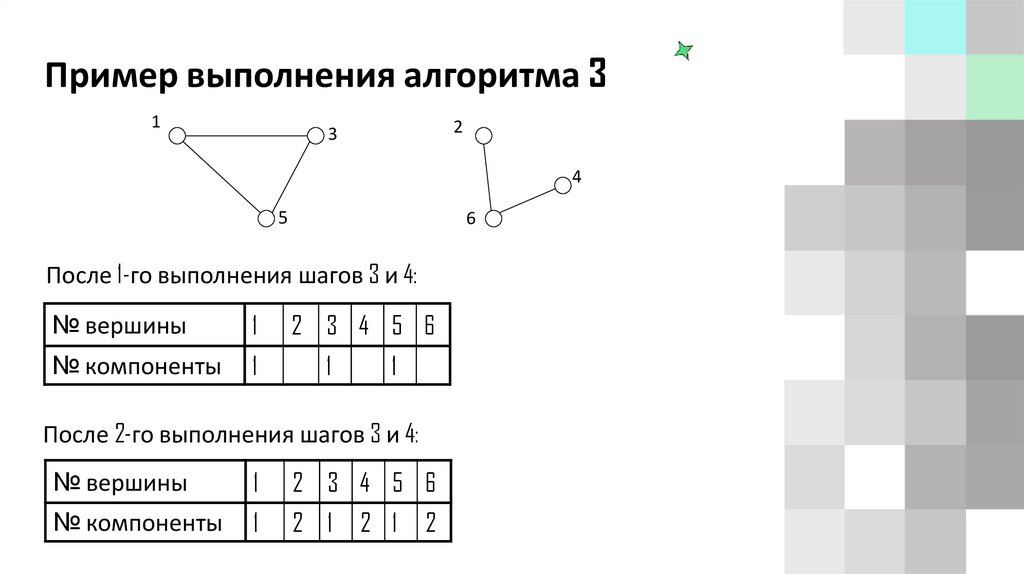
Пример выполнения алгоритма 3
1
2
3
4
5
6
После 1-го выполнения шагов 3 и 4:
№ вершины
1
№ компоненты
1
2 3 4 5 6
1
1
После 2-го выполнения шагов 3 и 4:
№ вершины
1
2 3 4 5 6
№ компоненты
1
2 1
2 1
2

12.

Задания для самостоятельной работы
1
Задан граф с 7 вершинами и рёбрами: (1,3), (1,6), (2,5), (3,4),
(3,5), (3,6), (3,7), (4,5), (4,6).
Алгоритмом 1 вычислить кратчайшие расстояния от 1-й
вершины для вершин: 1, 2, …, 7 и записать эти расстояния
через 1 пробел.
2
Для графа из задания 1 записать кратчайший путь через 1
пробел от вершины 1 до вершины 2.
3
Задан граф с 8 вершинами и рёбрами: (1,7), (2,4), (2,5), (3,8), (4,5),
(6,8). Алгоритмом 3 вычислить компоненты связности и
записать номера вершин
(по возрастанию) 2-й компоненты через 1 пробел.

13.

Спасибо за внимание