Дискретная математика в программировании. Часть X

1.

Дискретная математика
в программировании
Часть X
Костюк Ю.Л.
доктор технических наук, профессор

2.

Взвешенные графы
В отличии от обыкновенных графов и орграфов, рёбра во взвешенных графах имеют
дополнительный параметр – вес. Смысл этого параметра зависит от задачи.
Пример
города – вершины графа, дорога между двумя городами А и В – ребро (А,В), его вес –
это расстояние по дороге. В другом случае вес – это время проезда по дороге.
Веса рёбер во взвешенных графах могут быть как симметричными, когда вес ребра
(А,В) равен весу ребра (В,А), так и несимметричными, когда эти веса не равны друг
другу.
При изображении взвешенного графа каждое ребро подписывают его весом. В
графе с несимметричными весами рёбра изображают стрелками, как в орграфе.

3.

Минимальный остов
взвешенного графа
Если веса рёбер взвешенного графа симметричны, то задача состоит
в построении остова (каркаса) с минимальной суммой весов рёбер.
Для графа, представляющего города и дороги, минимальный остов – это сеть дорог
минимальной длины, связывающая все города.
Один из самых простых алгоритмов для решения этой задачи – алгоритм Прима.

4.

Алгоритм 10.
Построение минимального остова
Входные данные: взвешенный граф с симметричными весами рёбер
1
2
3
Вершины разделяются на два множества: множество А вершин, входящих
в остов, и множество В вершин, не включённых в остов. Вершина 1
включается в остов и переносится в множество А.
Если множество В пусто, то конец работы алгоритма.
В множестве В ищется такая вершина х, что ребро (x, y), где y принадлежит
множеству А, имеет минимальный вес. Ребро (x, y)
и вершина х включаются в остов, вершина х переносится
в множество А . Шаг 2 повторяется.

5.

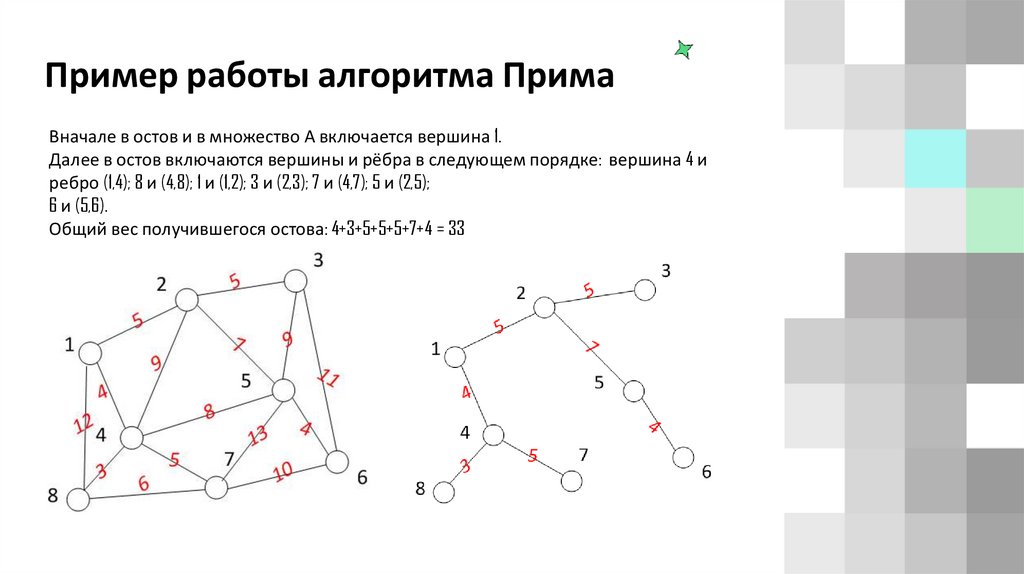
Пример работы алгоритма Прима
Вначале в остов и в множество А включается вершина 1.
Далее в остов включаются вершины и рёбра в следующем порядке: вершина 4 и
ребро (1,4); 8 и (4,8); 1 и (1,2); 3 и (2,3); 7 и (4,7); 5 и (2,5);
6 и (5,6).
Общий вес получившегося остова: 4+3+5+5+5+7+4 = 33

6.

Взвешенные графы
в виде матрицы весов
Рёбра и их веса во взвешенных графах удобно
задавать в виде матрицы весов (квадратная таблица
размером n x n, где n – число вершин). Строки и столбцы
в матрице помечаются номерами вершин. Вес ребра (i,
j) заносится
в i-ю строку, j-й столбец.
Если ребра (i, j) в графе нет, то заносится очень
большое число (изображается тире).
То же касается и диагональных элементов
(i, i). Веса рёбер при этом могут быть как
симметричные, так и нет.
Кроме того, нужна проверка того, что орграф связен,
т.е. состоит из одной компоненты связности. Это
можно сделать алгоритмом
1 и последующей проверкой того, что все вершины
просмотрены, т.е. попали в очередь.
1
2
3
4
5
6
7
8
1
–
5
–
4
–
–
–
12
2
5
–
5
9
7
–
–
–
3
–
5
–
–
9
11
–
–
4
4
9
–
–
8
–
5
3
5
–
7
9
8
–
4
13
–
6
–
–
11
–
4
–
10
–
7
–
–
–
5
13
10
–
6
8
12
–
–
3
–
–
6
–

7.

Кратчайшие расстояния
во взвешенном графе
Далее веса ребер и их сумму будем называть расстояниями.
Алгоритм Э. Дейкстры вычисляет кратчайшие расстояния от заданной
начальной вершины до всех остальных. В процессе работы вершины делятся
на два множества:
1
2
Множество А вершин, до которых уже вычислено самое кратчайшее
расстояние.
Множество В остальных вершин, до них вычислено кратчайшее
расстояние среди путей, проходящих только через вершины 1-го
множества.
Матрица расстояний в общем случае несимметричная.

8.

Алгоритм 11.
Вычисление кратчайших расстояний
Входные данные: взвешенный граф, заданный матрицей расстояний,
и начальная вершина а.
1
2
3
Расстояния до всех вершин записываются в набор (вектор) из n
расстояний. Первоначально в него копируются расстояния из строки а
матрицы. Вершина а переносится в множество А. Задаётся также вектор из
n ссылок. Первоначально в него для всех вершин (кроме а) записываются
ссылки на а. Для вершины а ссылка 0.
Если множество В пусто, то конец работы алгоритма.
В множестве В ищется такая вершина х, для которой вычисленное в
векторе расстояние минимально, и вершина х переносится
в множество А.

9.

Алгоритм 11.
Вычисление кратчайших расстояний
Затем для каждой вершины y из множества В делается коррекция: если для
неё расстояние s в векторе больше суммы расстояния до вершины х и длины
ребра (x, y), то в векторе расстояний это расстояние заменяется на эту сумму и
в векторе ссылок делается замена на х.
Шаг 2 повторяется.

10.

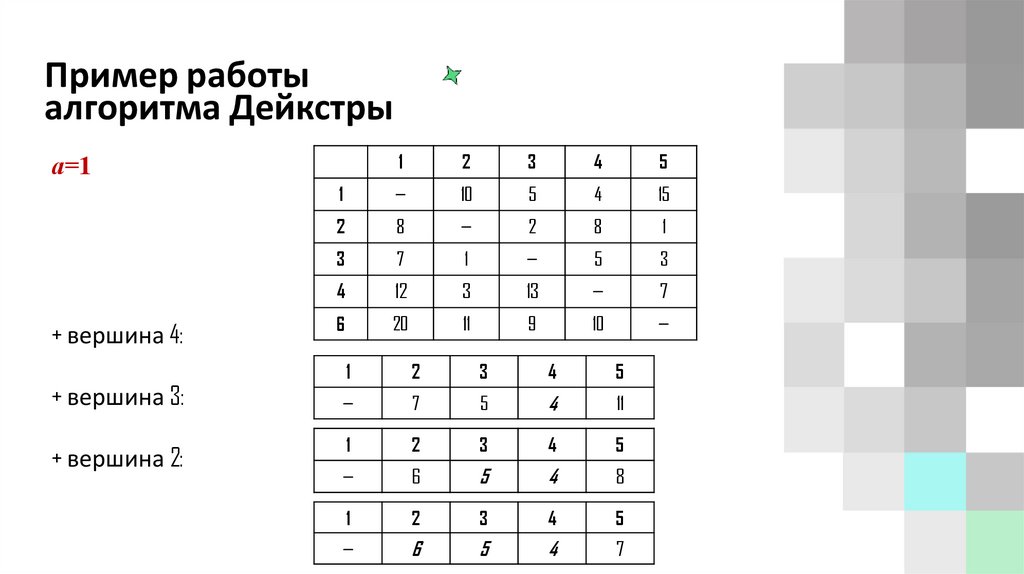
Пример работы
алгоритма Дейкстры
1
2
3
4
5
1
–
10
5
4
15
2
8
–
2
8
1
3
7
1
–
5
3
4
12
3
13
–
7
6
20
11
9
10
–
а=1
+ вершина 4:
+ вершина 3:
+ вершина 2:
1
2
3
4
5
–
7
5
4
11
1
2
3
4
5
–
6
5
4
8
1
2
3
4
5
–
6
5
4
7

11.

Пример работы
алгоритма Дейкстры
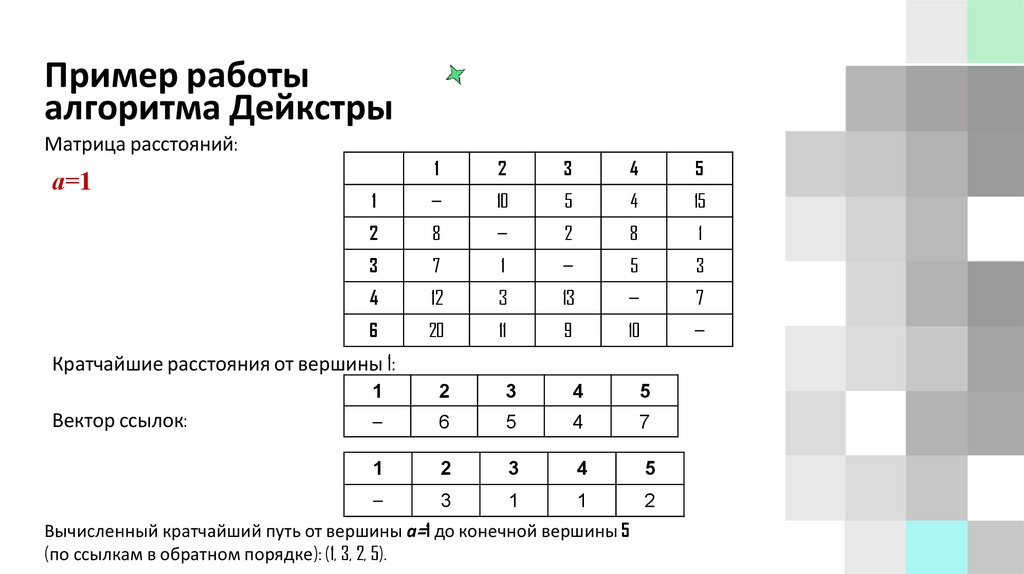
Матрица расстояний:
а=1
1
2
3
4
5
1
–
10
5
4
15
2
8
–
2
8
1
3
7
1
–
5
3
4
12
3
13
–
7
6
20
11
9
10
–
1
2
3
4
5
–
6
5
4
7
1
2
3
4
5
–
3
1
1
2
Кратчайшие расстояния от вершины 1:
Вектор ссылок:
Вычисленный кратчайший путь от вершины а=1 до конечной вершины 5
(по ссылкам в обратном порядке): (1, 3, 2, 5).

12.

Задача коммивояжёра
Коммивояжёру (бродячему торговцу) требуется посетить все города (каждый из
городов только один раз) и вернуться в начальный город так, чтобы его маршрут
был самым коротким.
Задача коммивояжёра на взвешенном графе: построить гамильтонов цикл
наименьшей длины. Матрица расстояний для этой задачи в общем случае
несимметричная.
Вычисление такого оптимального маршрута коммивояжёра можно осуществить
алгоритмом построения гамильтонова цикла, внеся в него несколько
дополнений.

13.

Вычисление
маршрута коммивояжёра
Дополнения к алгоритму 8 (построение гамильтонова цикла):
на 1-м шаге задать длину лучшего маршрута как очень большое число, длину
текущего маршрута – 0;
на 2-м шаге при добавлении в маршрут ещё одной вершины к длине текущего
маршрута добавить длину ребра;
на 2-м шаге при исключении из маршрута вершины из длины текущего маршрута
вычесть длину соответствующего ребра;
на 2-м шаге, когда новый маршрут построен, и его длина меньше запомненного
раньше лучшего маршрута, то запомнить новый маршрут
и его длину.

14.

Вычисление
маршрута коммивояжёра
Маршрут коммивояжёра
в изображённом ниже графе
(с симметричной матрицей
расстояний), полученный алгоритмом 8
с дополнениями:
(1, 2, 3, 5, 6, 7, 8, 4, 1).
Длина этого маршрута: 5+5+9+4+10+6+3+4
= 46

15.

Задания для самостоятельной работы
1
2
3
Задан взвешенный граф с симметричными длинами рёбер из
8 вершин и рёбрами (3-е число – длина ребра): (1,2;3), (1,3;4), (1,6;6),
(1,8,8), (2,3;10), (2,5;7),(2,8;5), (3,5;6), (3,7,11), (4,6;16), (4,7;14), (4,8;12), (4,8;12),
(5,7;9), (6,8;5). Алгоритмом 10 вычислить минимальный остов и
записать его длину
Для графа из задания 1 алгоритмом 11 вычислить
и записать длину кратчайшего пути из вершины 1
в вершину 7.
Для графа из задания 1 алгоритмом 8 (с дополнениями)
вычислить и записать минимальную длину маршрута
коммивояжёра.

16.

Спасибо за внимание