Похожие презентации:
Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса
1.
Условная вероятность. Правилоумножения вероятностей.
Формула полной вероятности.
Формула Байеса.
Презентация по физике преподавателя
« Орского технического техникума имени А. И. Стеценко » филиал пос. Энергетик
Николаевой Натальи Юрьевны
Оренбургская область
Новоорский район
посёлок Энергетик.
2.
Условная вероятностьВероятность события A при условии
того, что событие B произошло,
называется условной вероятностью и
обозначается
P A / B или PB A
3.
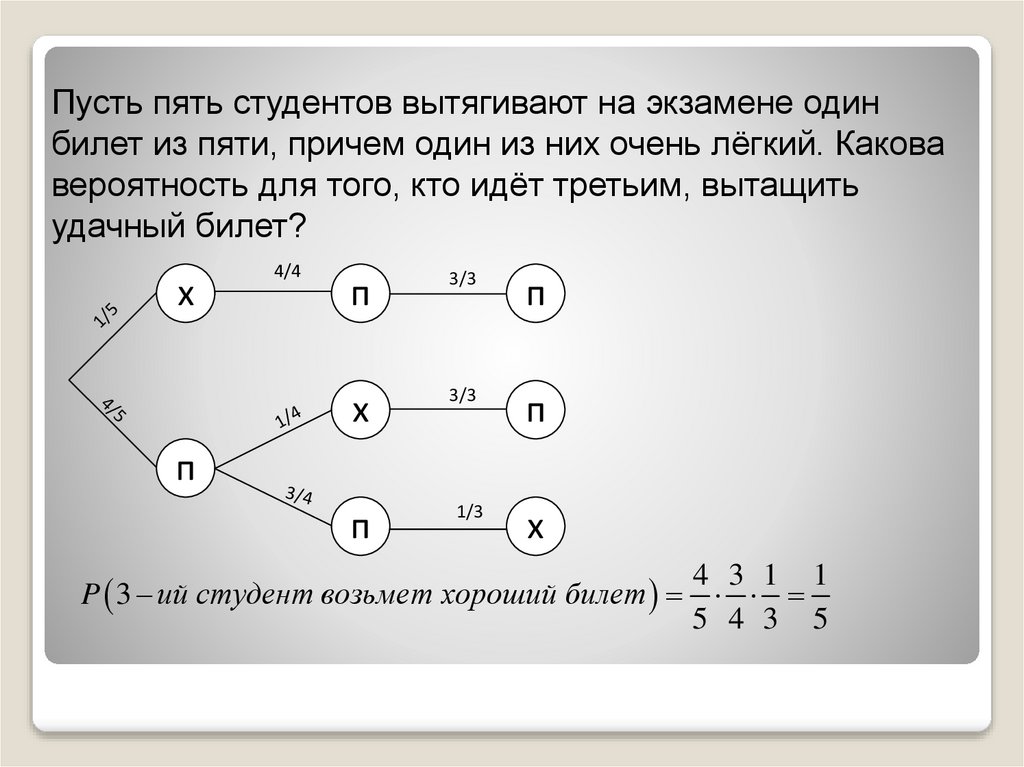
Пример 1.Пусть пять студентов вытягивают на экзамене один
билет из пяти, причем один из них - очень лёгкий.
Какова вероятность для того, кто идёт третьим,
вытащить удачный билет?
Решение.
Очевидно, что эта
вероятность зависит от того,
что попалось предыдущим
студентам, и вытянуть
удачный билет третий
студент может только в том
случае, когда его не взяли
двое предыдущих: P C
A B
4.
1/5
Пусть пять студентов вытягивают на экзамене один
билет из пяти, причем один из них очень лёгкий. Какова
вероятность для того, кто идёт третьим, вытащить
удачный билет?
х
4/4
5
4/
1/4
п
п
3/3
п
х
3/3
п
п
1/3
х
3/4
4 3 1 1
P 3 ий студент возьмет хороший билет
5 4 3 5
5.
Теорема умножения длянезависимых событий
Вероятность произведения двух
независимых событий А и В равна
произведению их вероятностей.
6.
ЗАДАЧА Если гроссмейстер А. играет белыми,то он выигрывает у гроссмейстера Б. с вероятностью
0,52. Если А. играет черными, то А. выигрывает у Б.
с вероятностью 0,3. Гроссмейстеры А. и Б. играют две
партии, причем во второй партии меняют цвет фигур.
Найдите вероятность того, что А. выиграет оба раза.
Решение.
ОбозначимС=ሼА выиграет белымиሽ;
D=ሼА выиграет чернымиሽ;
р(С)=0,52; р(D)=0,3; события независимы;
р(С D) р С р ( D ) 0,52 0,3 0,156
ОТВЕТ: 0,156
7.
Формула полной вероятностиДля вычисления полной вероятности события A
нужно перечислить все условия Hi, при которых
может наступить A, и перемножить вероятности
этих условий на соответствующие им условные
вероятности.
P A P H1 PH1 A P H 2 PH2 A ... P H k PHk A
Причем сумма вероятностей гипотез должна быть
равна 1, т.е.
P H 1
i
8.
Пусть событие A может быть вызванонабором причин Hi. Тогда вероятность
того, что к событию A привело событие
Hi, пропорциональна произведению
вероятности соответствующей причины
на вероятность следствия.
PA H i
P H i PHi A
P A
Формула Байеса
9.
Пример 2.Имеются 2 урны с шарами. В первой урне
находятся 2 белых и 4 черных шара, во второй – 3
белых и 3 черных.
Из каждой урны достали по одному шару. Найти
вероятность того, что эти шары белые.
Выбирается урна и из нее извлекается 2 шара. Найти
вероятность того, что эти шары белые. Найти
вероятность того, что они были взяты из первой
урны.
Из первой урны во вторую переложили 1 шар, а
затем из второй (пополненной) урны достали 2 шара.
Они оказались белыми. Найти вероятность того, что
был переложен белый шар.
10.
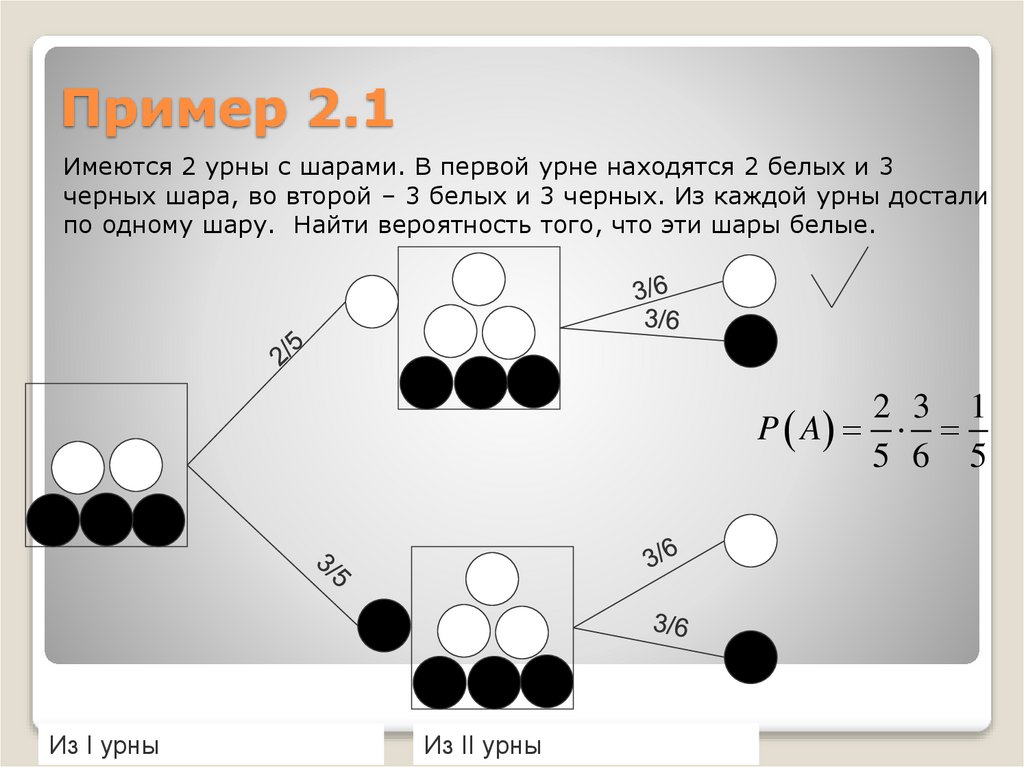
Пример 2.1Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3
черных шара, во второй – 3 белых и 3 черных. Из каждой урны достали
по одному шару. Найти вероятность того, что эти шары белые.
2 3 1
P A
5 6 5
Из I урны
Из II урны
11.
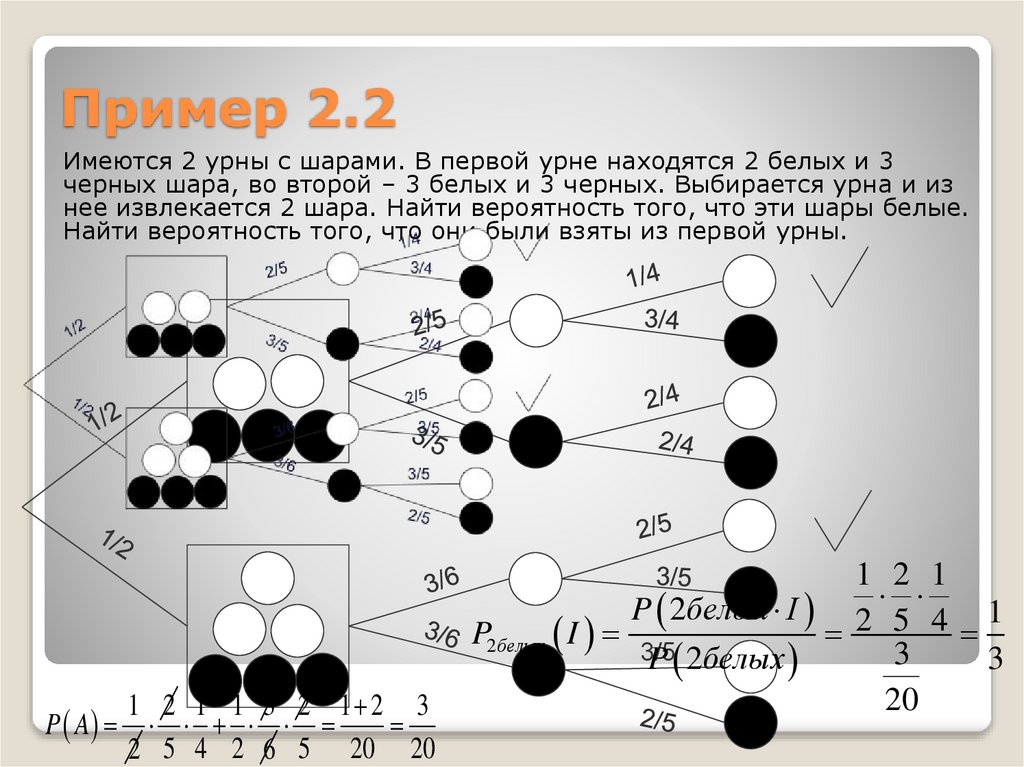
Пример 2.2Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3
черных шара, во второй – 3 белых и 3 черных. Выбирается урна и из
нее извлекается 2 шара. Найти вероятность того, что эти шары белые.
Найти вероятность того, что они были взяты из первой урны.
P A
1 2 1 1 3 2 1 2 3
2 5 4 2 6 5 20 20
1 2 1
P 2белых I 2 5 4 1
P2 белых I
3/5
3
P 2белых
3
20
12.
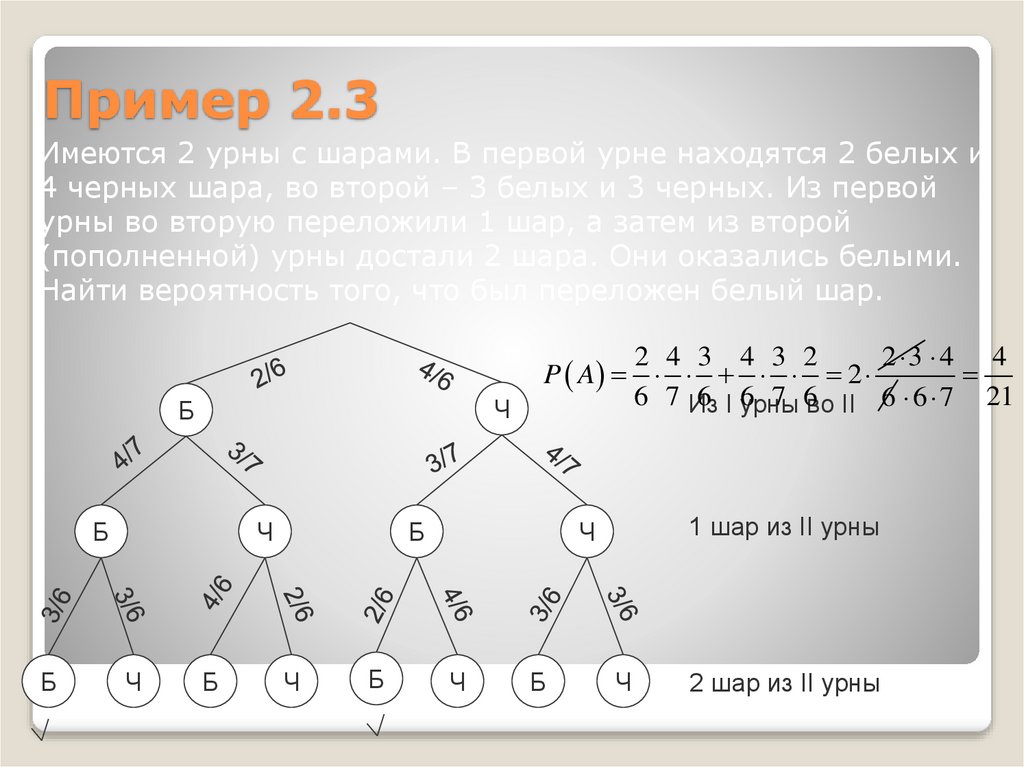
Пример 2.3Имеются 2 урны с шарами. В первой урне находятся 2 белых и
4 черных шара, во второй – 3 белых и 3 черных. Из первой
урны во вторую переложили 1 шар, а затем из второй
(пополненной) урны достали 2 шара. Они оказались белыми.
Найти вероятность того, что был переложен белый шар.
Ч
Б
Б
Б
Ч
Ч
Б
2 4 3 4 3 2
2 3 4 4
P A 2
6 7 Из
6 I6
7 6во II 6 6 7 21
урны
Б
Ч
Б
1 шар из II урны
Ч
Ч
Б
Ч
2 шар из II урны
13.
14.
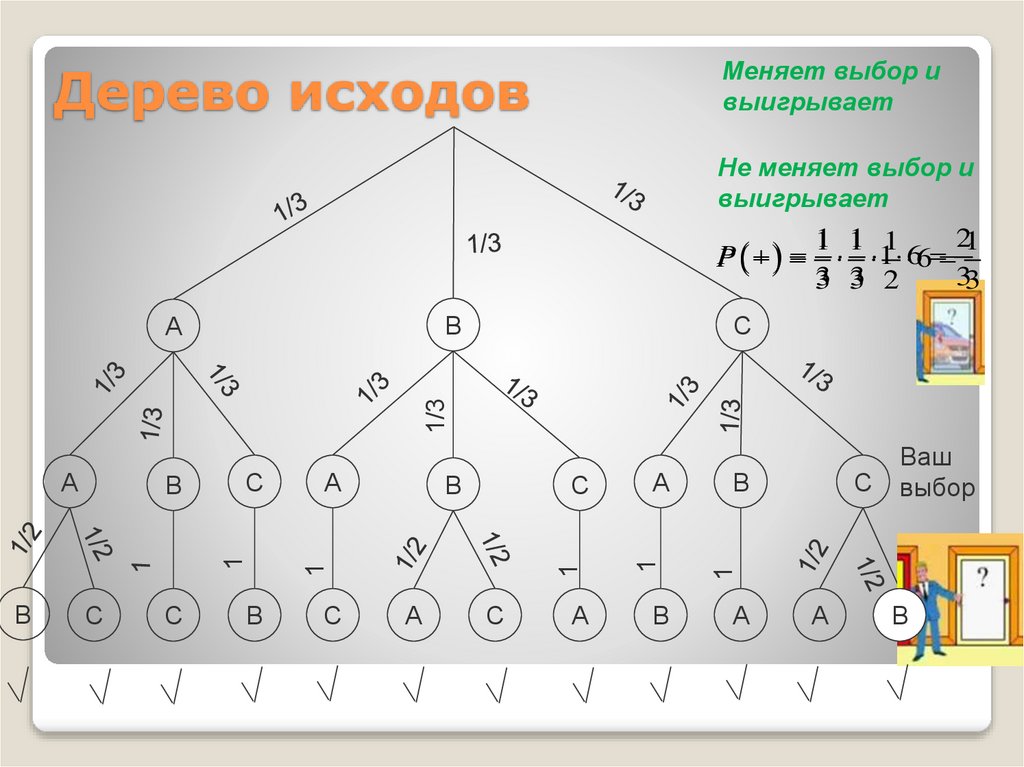
Меняет выбор ивыигрывает
Дерево исходов
Не меняет выбор и
выигрывает
P
B
C
B
C
B
A
C
C
A
B
1
C
A
1
C
C
1
B
B
1
A
1
1/3
A
1 1 1
21
1 66
33
3 3 2
A
B
A
C
A
Ваш
выбор
B
15.
Формула БайесаРассмотрим событие А, которое может
наступить лишь при
появления одного из
несовместных событий В1, В2, В3,…,Вn ,
образующих полную группу. Если событие А уже
произошло, то вероятность событий В1, В2,
В3,…,Вn можно определить по формуле Байеса
P ( Bi ) P( A / Bi )
P ( Bi / A)
Р ( А)
16.
Задача 1Два автомата производят одинаковые детали.
Производительность первого автомата в два раза больше
производительности второго. Вероятность производства
отличной детали у первого автомата равна 0,60, а у
второго 0,84. Наудачу взятая для проверки деталь
оказалась отличного качества.
Найти вероятность
того, что эта деталь произведена первым автоматом.
17.
РешениеСобытие А - деталь отличного качества.
Гипотезы:
В1 – деталь произведена первым автоматом,
,
так как этот автомат производит деталей в два раза
больше второго.
В2 – деталь изготовлена вторым автоматом,
Условные вероятности того, что деталь произведена
первым автоматом,
а вторым
Вероятность того, что наудачу взятая деталь окажется
отличного качества, вычисляем по формуле полной
вероятности:
.
18.
РешениеВероятность того, что взятая деталь изготовлена первым
автоматом, вычисляется по формуле Байеса:
19.
Задача 2Число грузовых машин, проезжающих по шоссе, на
котором стоит бензоколонка, относится к числу легковых
машин, проезжающих по тому же шоссе, как 4:1.
Вероятность того, что будет заправляться грузовая
машина, равна 0,2; для легковой машины эта вероятность
равна 0,3. К бензоколонке подъезжала для заправки
машина. Найти вероятность того, что эта машина грузовая
20.
РешениеCобытие A - машина заехала на заправку.
4
Гипотезы: H1 - это грузовая машина, P( H1 ) 0,8
5
H2 - это легковая машина, P( H ) 1 0,2
2
5
Условные вероятности: P( A / H ) 0,2; P( A / H ) 0,3
1
2
По формуле полной вероятности вероятность того, что
случайным образом выбранная из общего потока машина
зарулит на бензоколонку
P( A) 0,2 0,8 0,3 0,2 0,22
Искомую вероятность найдём по формуле Байеса
0, 2 0,8 8
P( H1 / A)
0,727
0, 22
11
Ответ: 0,727
21.
Задача 3Три студентки живут в одной комнате и по
очереди моют посуду. Вероятность разбить
тарелку для первой студентки равна 0.03, для
второй 0.01, для третьей - 0.04. На кухне раздался
звон разбитой тарелки. Найти вероятность того,
что третья студентка мыла тарелку.
22.
Событие A - разбили тарелку.Гипотезы:
H1 - тарелку разбила 1-я студентка, P(H1)=0,03
H2 - тарелку разбила 2-я студентка, P(H2)=0,01
H3 - тарелку разбила 3-я студентка, P(H3)=0,04
(гипотезы Н1,Н2,Н3 составляют полную группу
событий)
Условные вероятности (кто мыл посуду в момент
катастрофы):
1
P( A / H 1) P( A / H 2) P( A / H 3)
3
Решение
23.
РешениеПо формуле полной вероятности вероятность того,
что в процессе мытья посуды будет разбита тарелка
Искомую вероятность найдём по формуле Байеса
1
2
(переоценка
вероятности
события
H3
P( A) (0,03 0,01 0,04)
3
75
Ответ: 0,5
1
0,04
1
P( H 3 / A) 3
0,5
2
2
75
24.
Полная группа событийв результате данного
испытания обязательно
появится хотя бы одно из них.
25.
ТеоремаЕсли событие А может произойти только
вместе с одной из гипотез Н1, Н2…Нn,
образующих полную группу попарно
несовместных событий, то вероятность
события А
Р(А) = Р(Н1)РН1(А) + Р(Н2)РН2(А)
+ … + +Р(Нn)PHn(A)
Формула полной вероятности
26.
ПримерВ цехе работают 20 станков.
Из них 10 марки А, 6 марки В, и 4 марки
С.
Вероятности того, что деталь будет без
брака для этих станков соответственно
равны 0,9, 0,8 и 0,7.
Какова вероятность того, что наугад
выбранная деталь будет браком?
27.
ПримерСобытия
А = «Наугад выбранная деталь будет с
браком»
Н1 = «Деталь обработана на станке
марки А»
Н2 = «Деталь обработана на станке
марки В»
Н3 = «Деталь обработана на станке
марки С»
28.
ПримерВсего в цехе 20 станков
Р(Н1) = 10/20 = ½=0,5
Р(Н2) = 6/20 = 3/10 = 0,3
Р(Н3) = 4/20 = 1/5 = 0,2
Условные вероятности
PН1(А) = 1 – 0,9 = 0,1
PН2(А) = 1 – 0,8 = 0,2
PН3(А) = 1 – 0,7 = 0,3
29.
ПримерПо формуле полной вероятности
Р(А) = Р(Н1)·PН1(А) +
+ Р(Н2) ·PН2(А) +
+ Р(Н3) ·PН3(А) =
= 0,5·0,1 + 0,3·0,2 + 0,2·0,3 =
= 0,05 + 0,06 + 0,06 = 0,17
30.
ТеоремаЕсли событие А может произойти только
вместе с одной из гипотез Н1, Н2…Нn,
образующих полную группу попарно
несовместных событий, то вероятность
гипотез после испытания, когда событие
А уже имело место
РA(Нi) = Р(Нi)РНi(А) /Р(A)
Формула Байеса
31.
ПримерВ цехе работают 20 станков.
Из них 10 марки А, 6 марки В, и 4 марки
С. Вероятность того, что деталь будет
без брака для этих станков
соответственно равны 0,9, 0,8 и 0,7.
Наугад выбрали деталь. Она оказалась с
браком.
Какова вероятность того, что она была
изготовлена на станке марки В?
32.
ПримерСобытия
А = «Наугад выбранная деталь будет с
браком»
Н1 = «Деталь обработана на станке
марки А»
Н2 = «Деталь обработана на станке
марки В»
Н3 = «Деталь обработана на станке
марки С»
33.
ПримерР(Н2) = 0,3
PН2(А) = 0,2
Р(А) = 0,17
По формуле Байеса
РA(Н2) = Р(Н2) · РН2(А) / Р(A) =
= 0,3· 0,2 / 0,17 = 0,06 / 0,17 =
= 0,35
34.
ПримерПо формуле Байеса
РA(Н2) = Р(A) / (Р(Н2)РН2(А)) =
Р(А) = Р(Н1)·PН1(А) +
+ Р(Н2) ·PН2(А) +
+ Р(Н3) ·PН3(А) =
= 0,5·0,1 + 0,3·0,2 + 0,2·0,3 =
= 0,05 + 0,06 + 0,06 = 0,17





























 Математика
Математика Физика
Физика








