Математические предложения

1.

Составьте опорный конспект, используя
компьютерную презентацию, по теме
«Математические предложения»

2.

Математические
предложения

3. Введение

Понятие высказывания
Виды высказываний
Понятие высказывательной формы
Высказывания с кванторами
Операции над высказываниями
Операции над высказывательными
формами

4. Понятие высказывания

Высказывание (А,В,…)
– предложение, относительно которого имеет
смысл вопрос: истинно оно или ложно.
«Истина» и «ложь» называются значениями
истинности высказывания.
«Число 12 – четное» - «и»;
2 + 5 > 8 – «л».

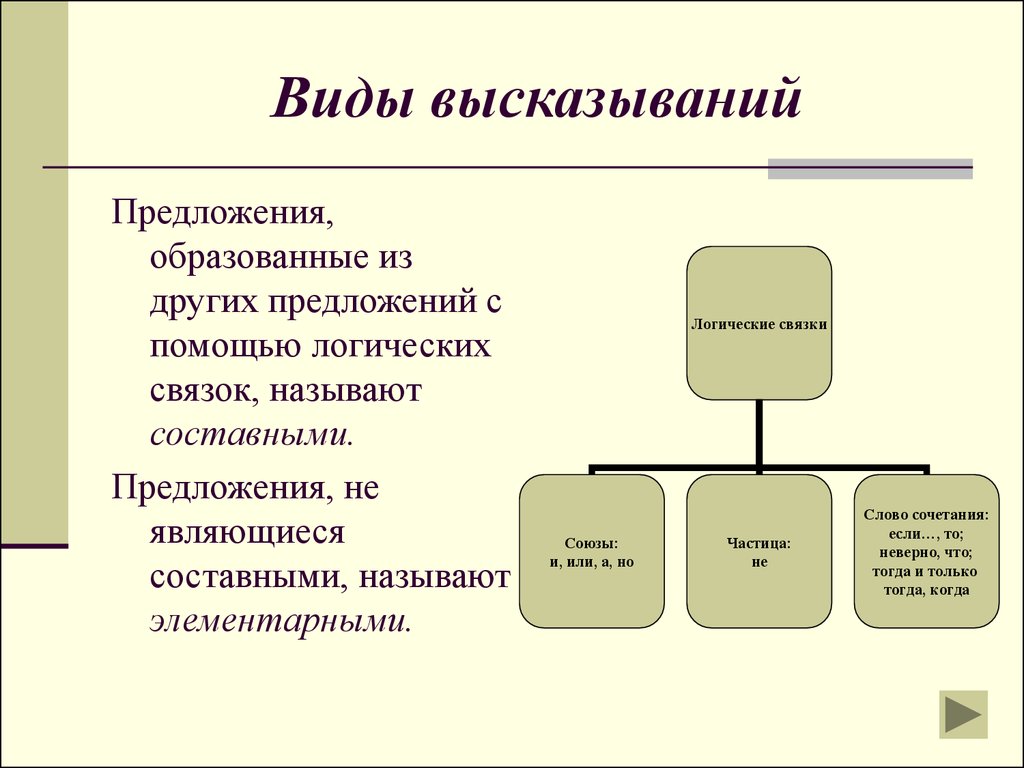
5. Виды высказываний

Предложения,
образованные из
других предложений с
помощью логических
связок, называют
составными.
Предложения, не
являющиеся
составными, называют
элементарными.
Логические связки
Союзы:
и, или, а, но
Частица:
не
Слово сочетания:
если…, то;
неверно, что;
тогда и только
тогда, когда

6.

«Если углы вертикальные, то они равны».
Из каких элементарных предложений образованно
составное предложение?
С помощью каких логических связок оно
образовано?
А – «углы вертикальные»
В – «углы равны»
Логическая связка – «если…, то»
Логическая структура (форма) – А В «если А, то В».

7. Понятие высказывательной формы (предиката)

Высказывательная форма (А(х), А(х;у), …)
– предложение с переменной, которое
обращается в высказывание при подстановке в
него значений переменной.
х + 5 = 8;
Число четное.

8.

Множество, из которого выбираются значения
переменной (переменных), входящей в
высказывательную форму, называется областью
определения высказывательной формы (Х).
Множество значений переменной, которые
обращают высказывательную форму в истинное
высказывание, называется множеством
истинности высказывательной формы (Т).
Т Х

9. Высказывания с кванторами

Выражение «для всякого х » в логике называется
квантором общности по переменной х и обозначается
символом х .
Запись ( х Х ) А( х) означает: «для всякого значения х
предложение А(х) – истинное высказывание».
Выражение «существует х такое, что… » в логике
называется квантором существования по переменной х
и обозначается символом х .
Запись ( х Х ) А( х) означает: «существует такое
значение х, что предложение А(х) – истинное
высказывание».

10.

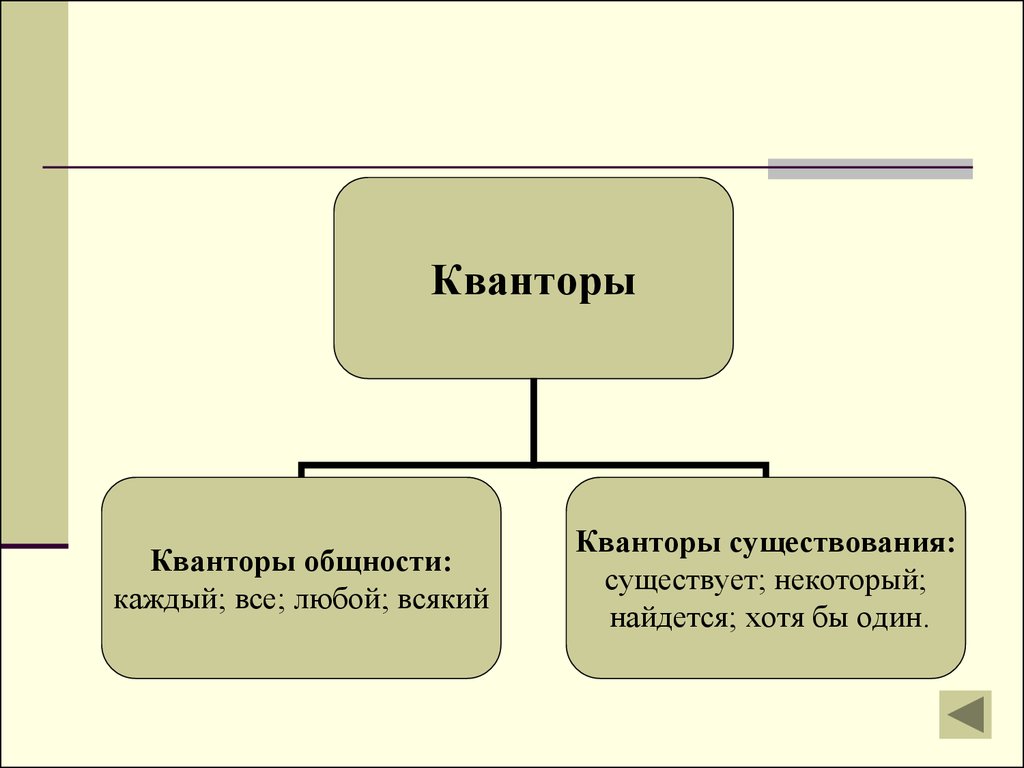
Кванторы
Кванторы общности:
каждый; все; любой; всякий
Кванторы существования:
существует; некоторый;
найдется; хотя бы один.

11. Операции над высказываниями

Конъюнкция
Дизъюнкция
Отрицание

12. Конъюнкция

Конъюнкцией высказываний А и В называется
высказывание вида А В («А и В»), которое
истинно, когда оба высказывания истинны, и
ложно, когда хотя бы одно из высказываний
ложно.
Таблица истинности конъюнкции
А
и
В
и
А В
и
л
л
и
л
л
л
л
л
и

13. Дизъюнкция

Дизъюнкцией высказываний А и В называется
высказывание вида А В («А или В»), которое
истинно, когда истинно хотя бы одно из
высказываний, и ложно, когда оба
высказывания ложны.
Таблица истинности дизъюнкции
А В
А
В
и
и
л
и
л
и
и
и
и
л
л
л

14. Отрицание

Отрицанием высказывания А называется
высказывание, истинное тогда и только тогда,
когда А ложно, и ложное, когда А истинно.
Отрицание высказывания обозначают А и
читают «неверно, что А».
Таблица истинности отрицания
А
А
и
л
л
и

15. Операции над высказывательными формами

Конъюнкция
Дизъюнкция
Отрицание

16. Конъюнкция

Конъюнкцию высказывательных форм А(х) и В(Х),
заданных на множестве Х, обозначают А( х) В ( х) .
Это предложение будет обращаться в истинное
высказывание при тех и только тех значениях х из
области Х, при которых обращаются в истинные
высказывания обе высказывательные формы.
Х
ТА
ТВ
Т А В Т А Т В

17. Дизъюнкция

Дизъюнкцию высказывательных форм А(х) и В(Х),
заданных на множестве Х, обозначают
А( х) В( х) .
Это предложение будет обращаться в истинное
высказывание при тех и только тех значениях х из
области Х, при которых обращается в истинное
высказывание хотя бы одна из высказывательных
форм.
Х
ТА
ТВ
Т А В Т А Т В

18. Отрицание

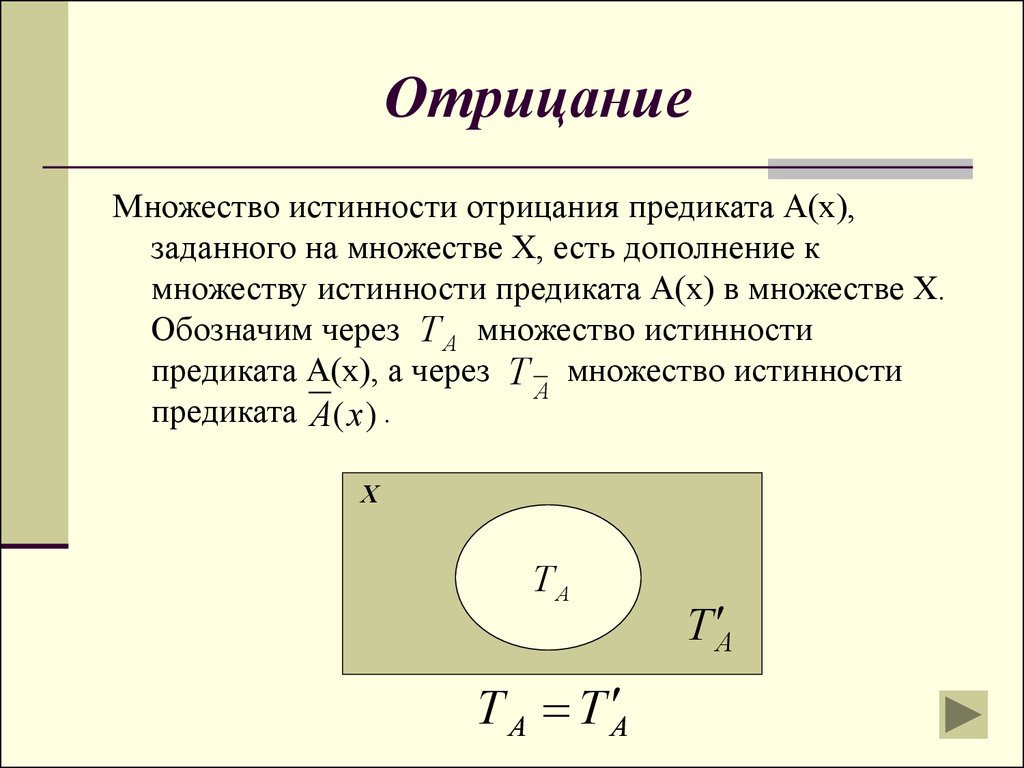
Множество истинности отрицания предиката А(х),
заданного на множестве Х, есть дополнение к
множеству истинности предиката А(х) в множестве Х.
Обозначим через Т А множество истинности
предиката А(х), а через Т А множество истинности
предиката А(х ) .
Х
ТА
Т А Т А
Т А

19.

Дополнительно изучите материал
учебников:
– [1], гл.1, §3, п.16 – 23;
– [2], гл.1, §2, п.5 – 10.