Гидравлические машины. Продолжение. Центробежные насосы. Часть 2. Лекция 12

1.

ГИДРАВЛИЧЕСКИЕ МАШИНЫ
Касабеков М.И.
для студентов специальности В056-5403
«Механика-прикладная математика»
Лекция 12
1
14.11.2023

2.

Продолжение
Центробежные насосы. Часть 2.
Лекция 12
2
14.11.2023

3.

Повестка дня
Основы теории подобия центробежных
насосов
Условия пропорциональности
Коэффициент быстроходности
Расширение области применения
центробежных насосов обточкой рабочих
колес
Работа насоса на сеть
Регулирование подачи центробежного насоса
Кавитация в насосах
Лекция 12
3
14.11.2023

4.

Основы теории подобия
центробежных насосов
Обобщение экспериментальных данных,
полученных при испытании модели, и
использование их при проектировании
натурных насосов возможно лишь при
соблюдении определенных правил,
устанавливаемых в теории подобия.
Лекция 12
4
14.11.2023

5.

Словарь
Явления называют подобными, если по
известным характеристикам одного из
них можно получить характеристики
другого простым пересчетом. При этом
в подобных системах должны
наблюдаться процессы одинаковой
физической природы.
Лекция 12
5
14.11.2023

6.

Для полного подобия насосов должно
выполняться их геометрическое,
кинематическое и динамическое
подобие.
Системы называются геометрически
подобными, если все соответственные их
линейные размеры пропорциональны, а
углы равны.
Лекция 12
6
14.11.2023

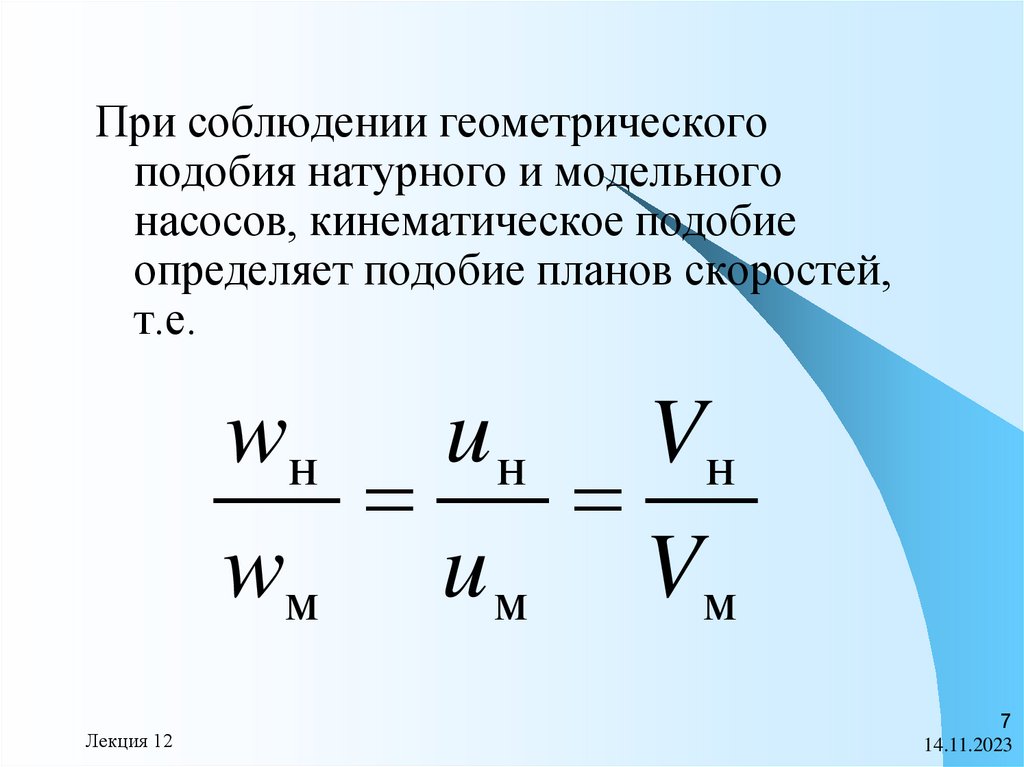
7.

При соблюдении геометрического
подобия натурного и модельного
насосов, кинематическое подобие
определяет подобие планов скоростей,
т.е.
wн u н Vн
wм u м Vм
Лекция 12
7
14.11.2023

8.

Для динамического подобия (подобия
сил) требуется равенство критериев
Рейнольдса у натуры и модели.
Критерий Рейнольдса для насоса
определяют по формуле
D
Re
2
2
Опыт показывает, что в большинстве случаев насосы
работают в области автомодельности, т.е. в области, в
которой характеристики насоса не зависят от
критерия Рейнольдса. Эта область наблюдается при
Re>1000.
Лекция 12
8
14.11.2023

9.

Обозначим отношение линейных
размеров натурного и модельного
насосов
k L rн rм
Лекция 12
9
14.11.2023

10.

Принимая во внимание, что угловая
скорость связана с частотой вращения
рабочего колеса следующим
соотношением
n 30
из условия кинематического подобия
получим
uн
rн н
nн
kL
u м rм м
nм
Лекция 12
10
14.11.2023

11.

Подобие подач.
Подача насоса связана с
геометрическими и кинематическими
характеристиками рабочего колеса
уравнением
Q V 2 м D 2 b2
V 2 sin 2 D 2 b2
Лекция 12
11
14.11.2023

12.

Отношение подач натурного и
модельного насосов
Qн
V2н sin 2н D2н b2н
Qм V2м sin 2м D2м b2м

13.

Поскольку у подобных насосов планы
скоростей подобны, то
2н 2м
наличие геометрического и
кинематического подобия позволяют
записать следующие равенства:
D2н b2н
V2н u 2н
nн
kL ;
kL
D2м b2м
V2м u 2м
nм
Лекция 12
13
14.11.2023

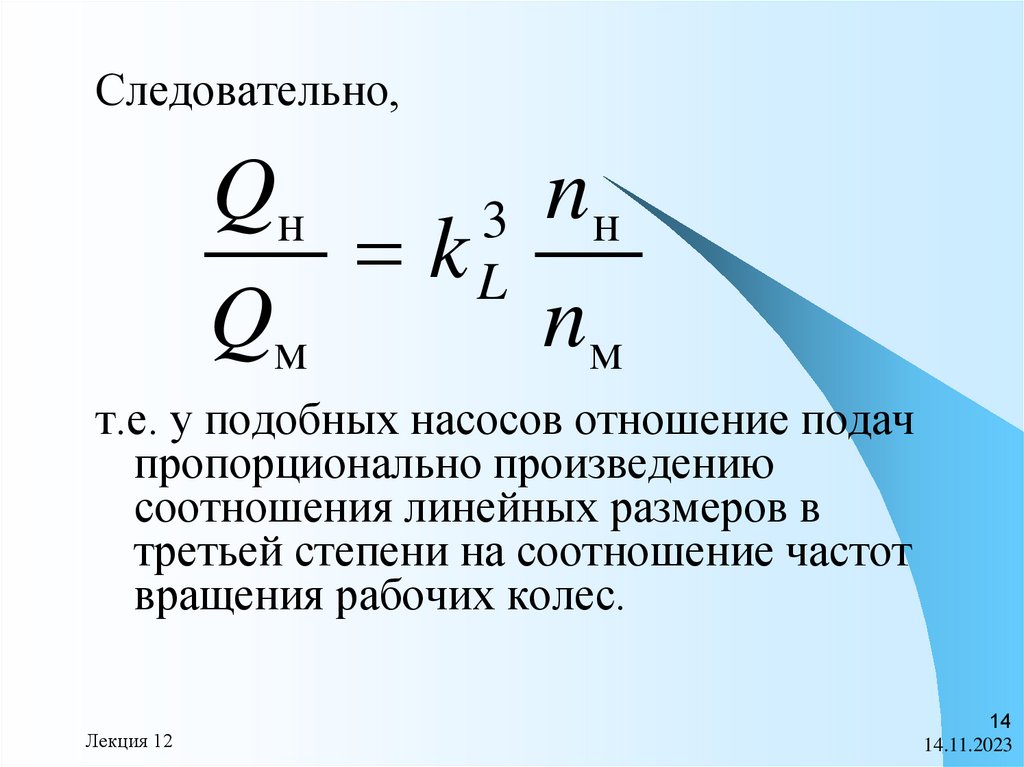
14.

Следовательно,
Qн
3 nн
kL
Qм
nм
т.е. у подобных насосов отношение подач
пропорционально произведению
соотношения линейных размеров в
третьей степени на соотношение частот
вращения рабочих колес.
Лекция 12
14
14.11.2023

15.

Подобие напоров.
Ранее были получены уравнения для
определения теоретического и
действительного напоров:
V2u u 2
Hт
g
Лекция 12
15
14.11.2023

16.

Полагая, что гидравлические КПД hг и
коэффициенты, учитывающие конечное
число лопаток e у модели и натуры
одинаковы, получим
H н V2 uн u 2н
n
2
н
k L
H м V2 uм u 2м
n
м
что отношение напоров у подобных
насосов пропорционально
произведению квадратов соотношений
линейных размеров и частот вращения
рабочих колес.
2

17.

Подобие мощностей.
Мощность насоса определяют по формуле
N
Лекция 12
Q gH
h
17
14.11.2023

18.

При работе натурного и модельного
насосов на одной и той же жидкости
м н
КПД модели и натуры приблизительно
одинаковы
hм hн
Лекция 12
18
14.11.2023

19.

При этих допущениях получим
N н Qн н gH нh м
N м Qм м gH мh н
Qн H н
n
5
н
k L
Qм H м
n
м
3

20.

Условия пропорциональности
Условия пропорциональности
позволяют производить пересчет
характеристик насоса на иную частоту
вращения.
С подобной задачей приходится
сталкиваться при замене двигателя у
насоса, либо при использовании
двигателя, который позволяет изменять
частоту вращения вала.
Лекция 12
20
14.11.2023

21.

Решение поставленной задачи основано
на представлении одного и того же
насоса, работающего при различных
частотах вращения (n1 и n2), как натуры
(1) и модели (2), выполненной в
масштабе 1:1 (kL=1).

22.

На основании теории подобия между
параметрами насоса имеют место
следующие соотношения:
Q1 n1
;
Q2 n 2
2
H 1 n1
;
H 2 n2
N1 n1
N 2 n2
Эти зависимости называют условиями
пропорциональности.
С их помощью, имея характеристики насоса,
работающего при одной частоте вращения,
можно построить характеристики, которые
будут иметь место при работе на другой
частоте.
3

23.

Словарь
Кривой подобных режимов называют
геометрическое место точек, режимы
работы насоса в которых, подобны
исходному.
Лекция 12
23
14.11.2023

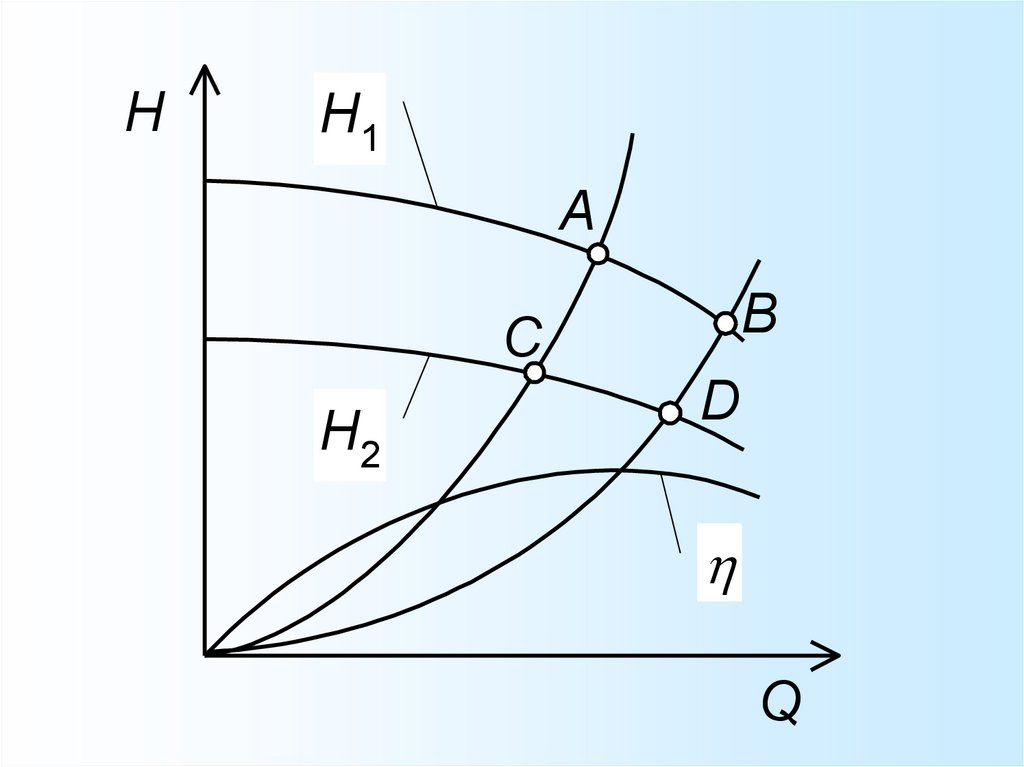
24.

H
1
H|n2
Для построения на напорной
характеристике насоса
кривой подобных режимов,
определим напоры и
подачи при различных
значениях частоты
H|n1 вращения.
2
H|n3
H=sQ2
Соединив полученные точки
плавной линией, получим
искомую кривую подобных
режимов.
Q
Лекция 12
24
14.11.2023

25.

Условия пропорциональности можно
представить в следующем виде:
2
2
Q1
H 1 n1
H 2 n2
Q2
или
H1 H 2
H
...
const
s
2
2
2
Q1
Q2
Q
Лекция 12
25
14.11.2023

26.

Последнее выражение позволяет записать
уравнение кривой подобных режимов:
H sQ
2
Условиями пропорциональности можно
пользоваться не для любых точек, а
лишь для тех, которые лежат на кривой
подобных режимов.
Лекция 12
26
14.11.2023

27.

Рассмотрим следующую задачу.
Предположим, что от насоса требуется
получить подачу Q2 при напоре H2,
причем эта режимная точка 2 не лежит
на характеристике насоса, построенной
для частоты вращения n1.
Требуется определить такую частоту
вращения n2, при которой напорная
характеристика H=f(Q) пройдет через
заданную точку 2.
Лекция 12
27
14.11.2023

28.

Определим по известным данным
коэффициент s для уравнения кривой
подобных режимов
s H2 Q
2
2
Лекция 12
28
14.11.2023

29.

Проведем параболу
H sQ
2
до пересечения с известной для частоты
n1 характеристикой насоса, т.е.
определим графически положение
точки 1, а, следовательно, и параметры
этой точки Q1 и H1.
Лекция 12
29
14.11.2023

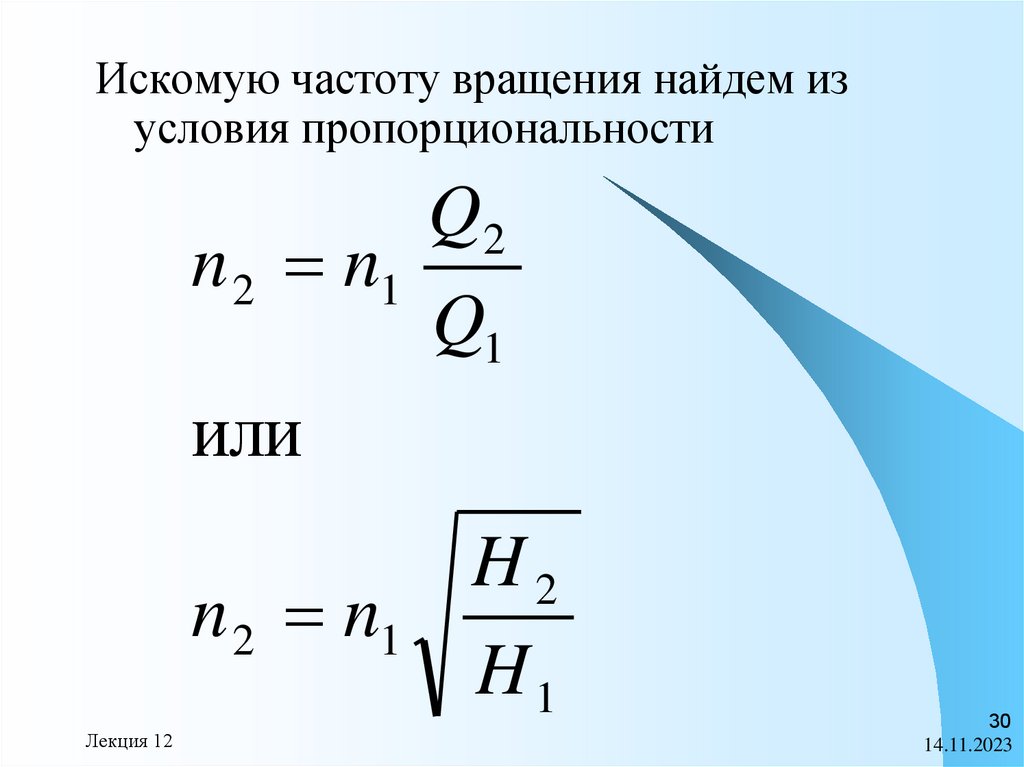
30.

Искомую частоту вращения найдем из
условия пропорциональности
Q2
n 2 n1
Q1
или
n 2 n1
Лекция 12
H2
H1
30
14.11.2023

31.

Коэффициент быстроходности
В настоящее время имеется большое
количество хорошо отработанных и
исследованных центробежных насосов
различного типа.
Для выбора из этого многообразия
прототипа для вновь проектируемого
насоса необходимо разработать
критерий, который позволял бы
сравнивать центробежные насосы
различной конструкции между собой.
Лекция 12
31
14.11.2023

32.

Поскольку при проектировании
заданными являются подача, напор и
частота вращения, то очевидно, что в
этот критерий необходимо включить
именно эти параметры.
Определив по заданным параметрам
численное значение такого критерия
для проектируемого насоса, и сравнив
его со значениями этого критерия для
имеющихся конструкций, получим
возможность подобрать в качестве
базового определенный тип насоса.
Лекция 12
32
14.11.2023

33.

Запишем условия подобия насосов "1" и "2",
приняв в качестве масштабного множителя
отношения наружных диаметров рабочих
колес
L
21
22
k D
D
3
Q1 n1 D 21
;
Q 2 n 2 D 22
2
Лекция 12
H 1 n1 D 21
H 2 n 2 D 22
2
33
14.11.2023

34.

Эти уравнения можно представить
следующим образом:
Q1
3
Q2
3
22
n1 D 21
n2 D
H1
H2
...
Q
q
,
3
nD2
H
...
h
2
2
2
2
2
2
n1 D 21 n 2 D 22
n D2

35.

Величины q и h получили названия
коэффициентов расхода и напора
соответственно.
Из приведенных соотношений следует,
что у подобных машин эти
коэффициенты одинаковы, т.е. их
можно использовать в качестве
критериев подобия.
Однако для конструктора эти критерии
неудобны, т.к. они содержат диаметр
рабочего колеса, который является
искомой величиной при
проектировании.
Лекция 12
35
14.11.2023

36.

Для его исключения находят отношение
квадрата коэффициента расхода на
коэффициент напора в третьей степени
2
4
q
n Q
3
3
h
H
Лекция 12
2
36
14.11.2023

37.

На практике в качестве критерия подобия
используют коэффициент
быстроходности ns
q
n s 3,65 3
h
2
Лекция 12
14
3,65n
Q
H
34
37
14.11.2023

38.

По величине коэффициента
быстроходности центробежные насосы
делят на:
тихоходные, ns = (40…80);
нормальные, ns = (80…150);
быстроходные, ns = (150…300).
Лекция 12
38
14.11.2023

39.

N
H,
N,
h
h
H
H h
N
H
h
N
h
D2
H
h
Q
Q
Тихоходные
центробежные
насосы
ns=40...80
D2/D0=2,5
Нормальные
центробежные
насосы
ns=80...150
D2/D0=2
Лекция 12
N
D0
D0
D1
H
D2
D2
D0
D2
D0=D1
H,
N,
h
Q
Быстроходные
центробежные
насосы
ns=150...300
D2/D0=1,8...1,4
Q
Диагональные
насосы
ns=300...600
D2/D0=1,2...1,1
N
Q
Пропеллерные
насосы
ns=600...1200
D2/D0=0,8
39
14.11.2023

40.

Расширение области применения
центробежных насосов обточкой
рабочих колес
Если от насоса требуется получить подачу Q'
и напор H', причем данная режимная точка
с указанными координатами лежит ниже
характеристики насоса, а изменение
частоты вращения двигателя невозможно,
то применяют обточку рабочего колеса по
наружному диаметру.
Лекция 12
40
14.11.2023

41.

При уменьшении наружного диаметра
рабочего колеса D2 окружная скорость
u2 на выходе из колеса уменьшается,
что ведет к снижению напора.
Следовательно, при обточке рабочего
колеса напорная характеристика насоса
понижается.
Лекция 12
41
14.11.2023

42.

Опыт показывает, что для расчета
характеристики центробежного насоса
после обточки рабочего органа можно
приближенно принять, что подача
изменяется пропорционально
наружному диаметру колеса в первой
степени, а напор – во второй степени:
Q D2
;
Q D2
Лекция 12
H D2
H D2
2
42
14.11.2023

43.

Экспериментально доказано, что для
режимов, удовлетворяющих данным
соотношениям, КПД насоса
приблизительно сохраняется
постоянным, если обточка рабочего
колеса не слишком велика.
Лекция 12
43
14.11.2023

44.

Объединив оба выражения, получим
H Q
H Q
2
или
H
H
c
2
2
Q
Q
откуда
H cQ
2
Следовательно, режимы, одинаковые для
обточенных колес, располагаются на
диаграмме с координатами H–Q на
параболе, вершина которой находится в
начале координат – параболе обточек.

45.

При обточке рабочего колеса по
наружному диаметру геометрическое
подобие нарушается, поэтому парабола
обточек не имеет ничего общего с
параболой подобных режимов.
В случае значительного уменьшения
диаметра в результате обточки КПД
насоса уменьшается, что является
ограничивающим фактором для
использования этого метода изменения
напорной характеристики.
Лекция 12
45
14.11.2023

46.

Предельная величина обточки зависит от
коэффициента быстроходности ns.
ns
D2 D2
D2
60
120
200
300
350
>350
0,2
0,15
0,11
0,09
0,07
0,00

47.

Насос выгодно эксплуатировать только в
области высоких КПД и больших высот
всасывания, поэтому следует
рассматривать не всю характеристику
насоса, а только ее часть,
соответствующую указанным
рекомендациям.
Лекция 12
47
14.11.2023

48.

Минимальная подача определяется
допустимым снижением КПД насоса по
сравнению с его максимальным
значением;
максимальная подача – также
допустимым снижением КПД, или
допустимым повышением
кавитационного запаса, который при
подачах, больших оптимальной, резко
возрастает.
Лекция 12
48
14.11.2023

49.

H
H1
A
B
C
H2
D
h
Q

50.

Предположим, что линия H1 представляет
собой характеристику необточенного
колеса, а H2 – характеристику при
максимальной обточке колеса. Участок
А–В характеристики является рабочим,
т.е. соответствует максимальному КПД.
Точки С и D построены с помощью
парабол обточек и ограничивают
оптимальную рабочую зону
максимально обточенного колеса.
Лекция 12
50
14.11.2023

51.

Область АВСD включает все точки
характеристик обточенных колес,
удовлетворяющих требованиям
максимальной экономичности.
Четырехугольник АВСD называют полем
насоса.
Сводный график полей центробежных насосов
приводят в каталогах насосов.
По заданным значениям подачи и напора на
сводном графике находят режимную точку,
которая попадает на поле какого-то
конкретного насоса, который обеспечит
наибольший КПД на указанном режиме.
На поле насоса приводится его марка и
частота вращения.
51
Лекция 12
14.11.2023

52.

Работа насоса на сеть
Совокупность насоса, расходного и
напорного резервуаров, трубопроводов,
связывающих вышеперечисленные
элементы, регулирующей и запорной
арматуры, а также контрольноизмерительной аппаратуры составляет
насосную установку.
Лекция 12
52
14.11.2023

53.

Для перемещения жидкости по трубопроводам
из расходного резервуара в напорный
необходимо затрачивать энергию на:
подъем жидкости на высоту Hг, равную
разности уровней в резервуарах (эту величину
называют геометрическим напором насосной
установки);
преодоление разности давлений в них pр и
pн;
преодоление суммарных гидравлических
потерь Shп во всасывающем и напорном
трубопроводах.
Лекция 12
53
14.11.2023

54.

Таким образом, энергия, необходимая для
перемещения единицы веса жидкости
из расходного резервуара в напорный
по трубопроводам, или потребный
напор установки определяется по
выражению
H потр H г
Лекция 12
pн pр
g
hп
54
14.11.2023

55.

Характеристикой насосной установки
называют зависимость потребного
напора от расхода жидкости.
Геометрический напор Hг, давления pр и
pн от расхода не зависят.
Гидравлические потери являются
функцией расхода и зависят от режима
движения.

56.

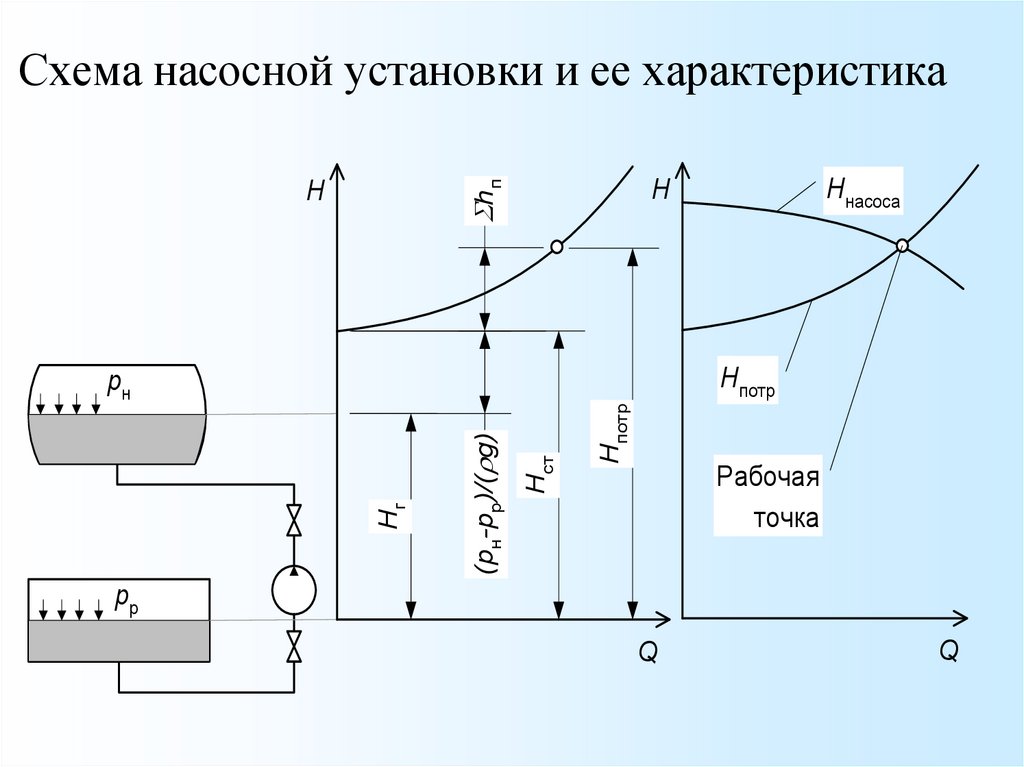
Схема насосной установки и ее характеристика
Hнасоса
H
S hп
H
Hст
(pн-pр)/( g)
Hг
Hпотр
Hпотр
pн
Рабочая
точка
pр
Q
Q

57.

Насос работает на таком режиме, при котором
потребный напор равен напору насоса.
Для определения режима работы насоса
необходимо на одном и том же графике в
одинаковых масштабах нанести
характеристику насоса и насосной
установки.
Точка пересечения характеристик называется
рабочей точкой.
Ограничением в широком распространении
центробежных насосов в значительной мере
является неспособностью их к сухому
всасыванию.
Лекция 12
57
14.11.2023

58.

Регулирование подачи
центробежного насоса
Количество жидкости, подаваемой
насосом в сеть, определяется нуждами
потребителей. Поэтому на практике
почти всегда приходится прибегать к
регулированию подачи, которая
достигается дросселированием
напорного трубопровода и изменением
частоты вращения рабочего колеса.
Лекция 12
58
14.11.2023

59.

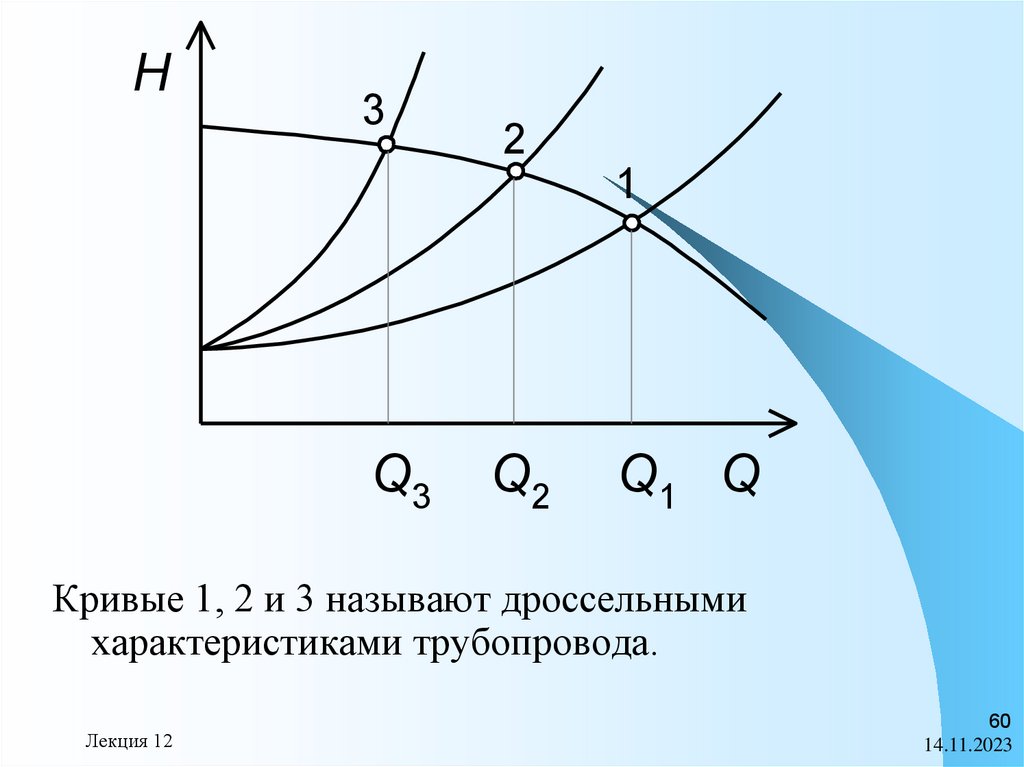
Дроссельное регулирование.
Каждая насосная установка оснащается
запорной задвижкой, устанавливаемой
за насосом. При уменьшении расхода в
сети возникает необходимость изменить
подачу насоса. Прикрывая задвижку,
изменяют (увеличивают) сопротивление
системы. Создаваемый насосом напор
увеличивается. Это приводит к
снижению подачи в соответствии с
характеристикой насоса.
Лекция 12
59
14.11.2023

60.

H
3
2
1
Q3
Q2
Q1 Q
Кривые 1, 2 и 3 называют дроссельными
характеристиками трубопровода.
Лекция 12
60
14.11.2023

61.

Дроссельным способом регулирования
можно менять подачу в широком
диапазоне. Этот вид регулирования
прост, надежен и наиболее часто
применяется при эксплуатации насосных
установок. Но он требует
дополнительных затрат энергии на
преодоление потерь в задвижке.
Лекция 12
61
14.11.2023

62.

Регулирование работы насоса
изменением частоты вращения
рабочего колеса.
В основе этого способа лежит закон
пропорциональности, из которого
следует
ni
ni
Qi Q0
; H i H 0
n0
n
0
Лекция 12
2
62
14.11.2023

63.

С помощью этих уравнений можно
произвести перестроение
характеристики насоса H0=f(Q0) при
номинальной частоте вращения
рабочего колеса n0 на любую иную
частоту вращения ni.
Лекция 12
63
14.11.2023

64.

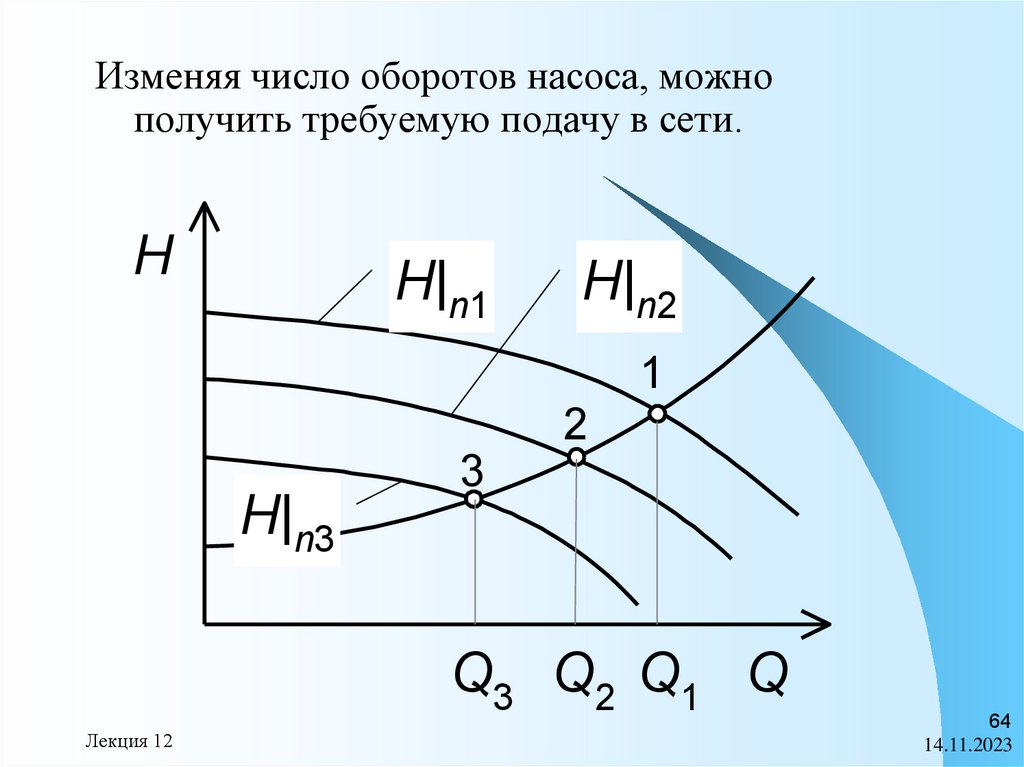
Изменяя число оборотов насоса, можно
получить требуемую подачу в сети.
H
H|n1
H|n2
1
2
H|n3
3
Q3 Q2 Q1 Q
Лекция 12
64
14.11.2023

65.

Рассматриваемый способ регулирования
не вызывает дополнительных потерь
энергии, поскольку напор в сети
соответствует напору, развиваемому
насосом.
Недостаток этого способа изменения
подачи состоит в использовании более
дорогого привода насоса с
регулируемой частотой вращения.
Лекция 12
65
14.11.2023

66.

Для увеличения подачи жидкости
осуществляют параллельную работу
нескольких насосов. Построение
результирующей характеристики такой
системы производят путем сложения подач
каждого из насосов при одинаковых
значениях напоров.
Когда требуется повысить напор в системе,
используют последовательное соединение
нескольких насосов. В этом случае
результирующую характеристику получают
сложением напоров каждого из насосов при
одинаковых значениях подач.
Лекция 12
66
14.11.2023

67.

Кавитация в насосах
Под кавитацией понимают комплекс механических и
электрохимических явлений возникающих в потоке в
результате снижения давления ниже давления
насыщения жидкости при данной температуре.
При этом из жидкости начинают выделяться пар и
растворенные в ней газы.
Кавитация сопровождается шумом, ухудшением
энергетических характеристик насоса и разрушением
его конструктивных элементов.
При развитой кавитации, когда паро-газо-водяная смесь
заполняет все межлопаточное пространство,
происходит разрыв сплошности потока и "срыв"
(прекращение) подачи.
Лекция 12
67
14.11.2023

68.

Согласно ударной гипотезе
кавитационного разрушения в зоне
"схлопывания" кавитационного
пузырька давление достигает весьма
больших значений, возникают местные
гидравлические удары, которые, в
конечном итоге, приводят к
разрушению металла.
Лекция 12
68
14.11.2023

69.

Для безкавитационной работы насоса
необходимо соблюдать требование:
минимальное абсолютное давление в
насосе должно быть больше давления
насыщения при данной температуре
pmin ps
Лекция 12
69
14.11.2023

70.

Величиной, характеризующей
безкавитационную работу насоса,
является кавитационный запас –
разность между удельной энергией
потока на входе насоса и энергией,
соответствующей давлению насыщения.
p вх V p s
h
g
2
g
g
2
вх

71.

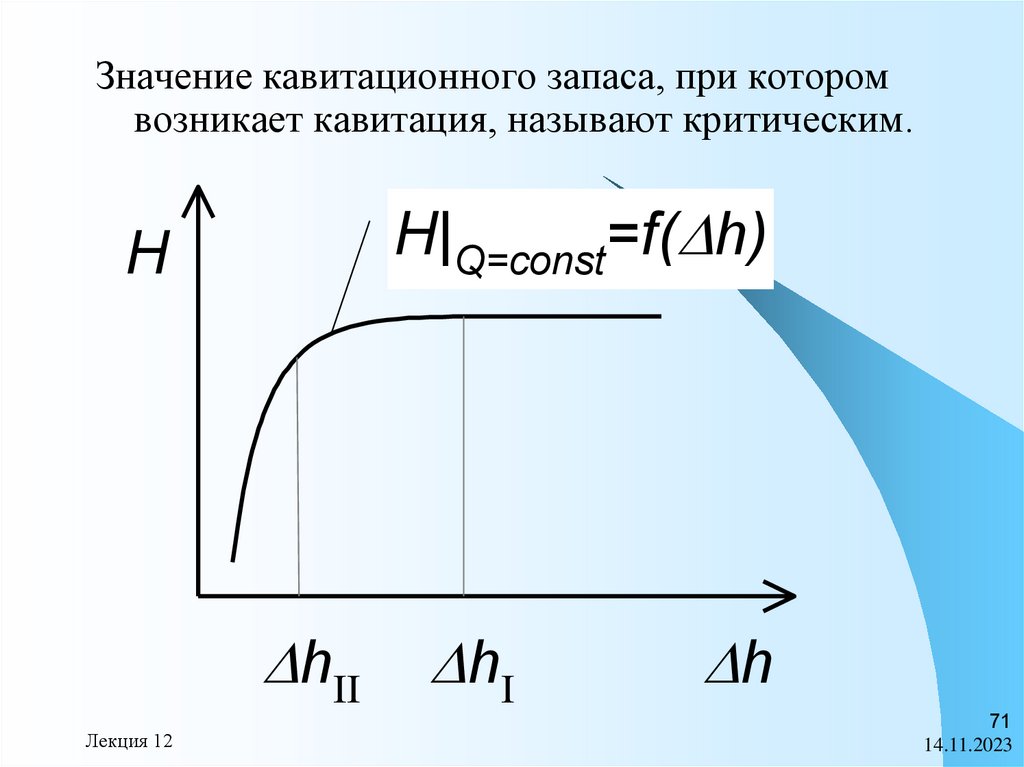
Значение кавитационного запаса, при котором
возникает кавитация, называют критическим.
H|Q=const=f( h)
H
hII
Лекция 12
hI
h
71
14.11.2023

72.

Режим работы насоса, когда при
неизменной подаче начинается падение
напора, называют первым критическим
режимом. Ему соответствует первый
критический кавитационный запас hI.
При дальнейшем уменьшении
кавитационного запаса h
кавитационная каверна расширяется и
приближается к концу рабочей лопатки.
При некотором значении hII она теряет
устойчивость, и это сопровождается
резким снижением напора.
Лекция 12
72
14.11.2023

73.

Для того чтобы насос не работал в
режиме кавитации из-за неточности
учета всех факторов на нее влияющих, в
качестве допустимого кавитационного
запаса принимают величину, на
(10…30)% большую hI, то есть
hдоп 1,1... 1,3 hI
Лекция 12
73
14.11.2023

74.

Выразим удельную энергию потока на
входе в насос из уравнения Бернулли,
записанного для участка всасывающего
трубопровода, расположенного между
сечениями, соответствующими
свободной поверхности жидкости и
входному патрубку насоса.
2
вх
pa
V
p вх
hг hпот
2g
g g
Лекция 12
74
14.11.2023

75.

Подставим полученное выражение в
уравнение для определения
кавитационнго запаса
pa ps
h
hг hпот
g
Лекция 12
75
14.11.2023

76.

Заменим h на допустимый кавитационный
запас.
Выразим из последней зависимости высоту
всасывания.
Найденная величина представляет собой
допустимую высоту всасывания
h
доп
г
pa ps
hдоп hпот
g
превышение которой при монтаже насоса
приведет к описанным здесь негативным
явлениям.
Лекция 12
76
14.11.2023