Перестановки, размещения и сочетания

1.

14.11.2023
К л а с с н а я р а б о т а.
Перестановки, размещения
и сочетания.

2.

1. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 2 космонавтов для экспедиции к далеким
планетам?
Космонавты: 1, 2, 3, 4, 5, 6, 7.
12 13 14 15 16 17
21 23 24 25 26 27
34 35 36 37
45 46 47
56 57
67
21 способ

3.

2. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 2 космонавтов: Командира корабля и
Бортинженера для экспедиции к далеким планетам?
Космонавты: 1, 2, 3, 4, 5, 6, 7.
КБ: 12 13 14 15 16 17
21 23 24 25 26 27
31 32 34 35 36 37
41 42 43 45 46 47
51 52 53 54 56 57
61 62 63 64 65 67
71 72 73 74 75 76
42 способа
Во сколько раз будет
больше способов?
№ 1. Неупорядоченная выборка
№ 2. Упорядоченная
выборка

4.

2. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 2 космонавтов: Командира корабля и
Бортинженера для экспедиции к далеким планетам?
Космонавты: 1, 2, 3, 4, 5, 6, 7.
2 способ
Сколькими способами можно выбрать капитана?
Сколькими способами из оставшихся
космонавтов можно выбрать Бортинженера?
7 · 6 = 42 способа

5.

3. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 3 космонавтов: Командира корабля, Бортинженера и космонавта-Исследователя для экспедиции к далеким планетам?
Космонавты: 1, 2, 3, 4, 5, 6, 7.
КБИ: 7 · 6 · 5 = 210 способов
4. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 4 космонавтов: Командира корабля, Бортинженера, космонавта-Исследователя и Навигатора
для экспедиции к далеким планетам?
КБИН: 7 · 6 · 5 · 4 = 840 способов

6.

5. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 5 космонавтов: Командира корабля, Бортинженера, космонавта-Исследователя, Навигатора и
Астробиолога для экспедиции к далеким планетам?
КБИНА:
7 · 6 · 5 · 4 · 3 = 2520 способов
6. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 6 космонавтов: Командира корабля, Бортинженера, космонавта-Исследователя, Навигатора,
Астробиолога и Медика для экспедиции к далеким
планетам?
КБИНАМ: 7 · 6 · 5 · 4 · 3 · 2 = 5040 способов

7.

7. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 7 космонавтов: Командира корабля, Бортинженера, космонавта-Исследователя, Навигатора,
Астробиолога, Медика и Фотографа для экспедиции
к далеким планетам?
КБИНАМФ: 7! = 5040 способов
Определение.
Перестановкой называется множество из n элементов, записанных в определённом порядке.
Рn = n!

8.

3. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 3 космонавтов: Командира корабля, Бортинженера и космонавта-Исследователя для экспедиции к далеким планетам?
7!
КБИ: 7 · 6 · 5 · 4 · 3 · 2 · 1 = 7! =
3
=
А
7
4!
(7
–
3)!
4·3·2·1
«Число размещений из 7 по 3»
Количество упорядоченных k – элементных подмножеств из n – элементного множества это число
размещений из n по k:
n!
А =
( n k )!
k
n

9.

1. В отряде космонавтов 7 человек одинаковой квалификации. Сколькими способами можно выбрать
из них 2 космонавтов для экспедиции к далеким
планетам?
Космонавты: 1, 2, 3, 4, 5, 6, 7.
12 13 14 15 16 17
21 23 24 25 26 27
34 35 36 37
Неупорядоченная
выборка
А 27
C27 = 2
!
45 46 47
«Число сочетаний из 7 по 2»
56 57
21 способ
67

10.

Количество неупорядоченных k – элементных подмножеств из n – элементного множества это число
сочетаний из n по k:
k
А
C kn = n
k!
n!
C =
k!(n k )!
k
n

11.

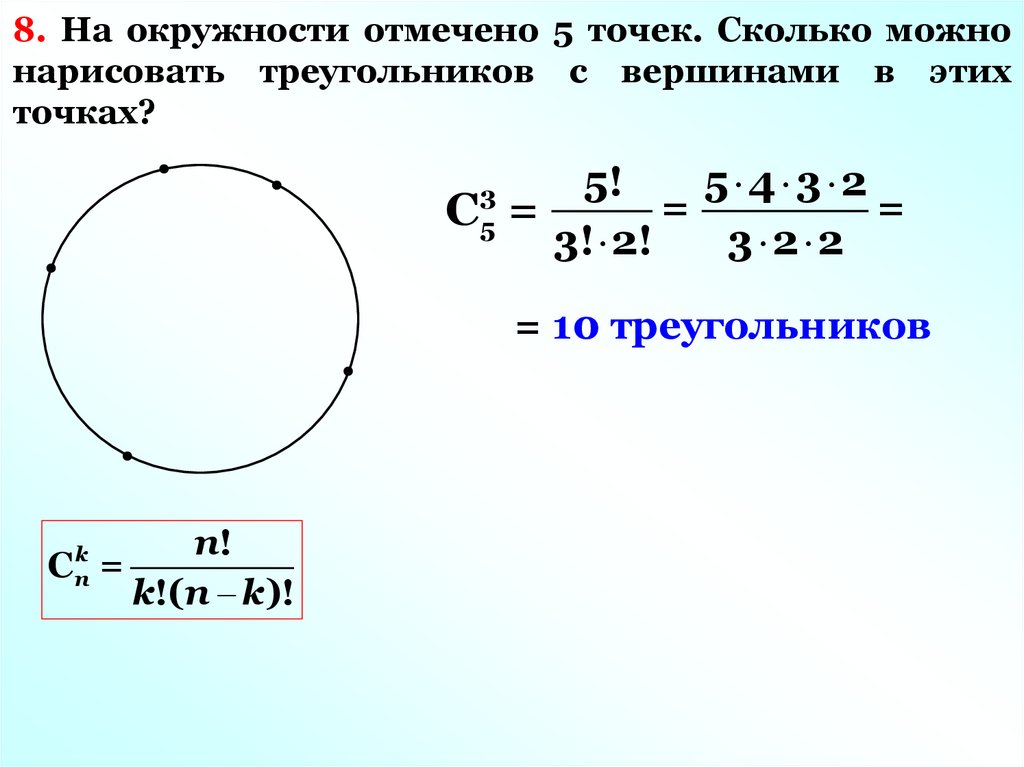
8. На окружности отмечено 5 точек. Сколько можно
нарисовать треугольников с вершинами в этих
точках?
5!
5 4 3 2
=
=
C =
3 2 2
3! 2!
3
5
= 10 треугольников
n!
C =
k!(n k )!
k
n

12.

9. Чемпионат России по шахматам проводится в один
круг: каждый игрок играет ровно по одной партии со
всеми другими. Сколько играется партий, если в чемпионате участвует 18 шахматистов?
Каждая партия – выбор двоих из 18 шахматистов.
C
2
18
18!
18 17 16!
=
= 9 · 17 = 153 партии
=
2! 16!
2 16!
n!
C =
k!(n k )!
k
n

13.

10. В лототроне находится 90 шаров с номерами от 10
до 99. Ведущий последовательно достаёт три шара и
кладёт их рядом так, чтобы получилось шестизначное число. Сколько вариантов шестизначных чисел
может получиться?
А
3
90
90! 90 89 88 87!
=
= 704880 в-в
=
87!
87!
n!
А =
( n k )!
k
n

14.

1. В математическом кружке занимается 10 человек. Сколькими способами можно составить из
них команду из четырёх человек для командной
олимпиады?
2. Сколько трёхзначных чисел может быть составлено из нечётных цифр так, чтобы цифры в
каждом числе не повторялись?