Закон сохранения энергии

1.

Закон сохранения энергии

2.

Камень массой 1 кг брошен вертикально вверх
с начальной скоростью 4 м/с.
На сколько увеличится потенциальная энергия камня
от начала движения к тому времени, когда скорость
камня
уменьшится до 2 м/с?
(Ответ дайте в джоулях.)
Ответ: 6.

3.

• Мальчик столкнул санки с вершины горки.
Сразу после толчка санки имели скорость
5 м/с. Высота горки 10 м. Трение санок о
снег пренебрежимо мало. Какова скорость
санок у подножия горки? (Ответ дайте в
метрах в секунду.)
Ответ: 15.

4.

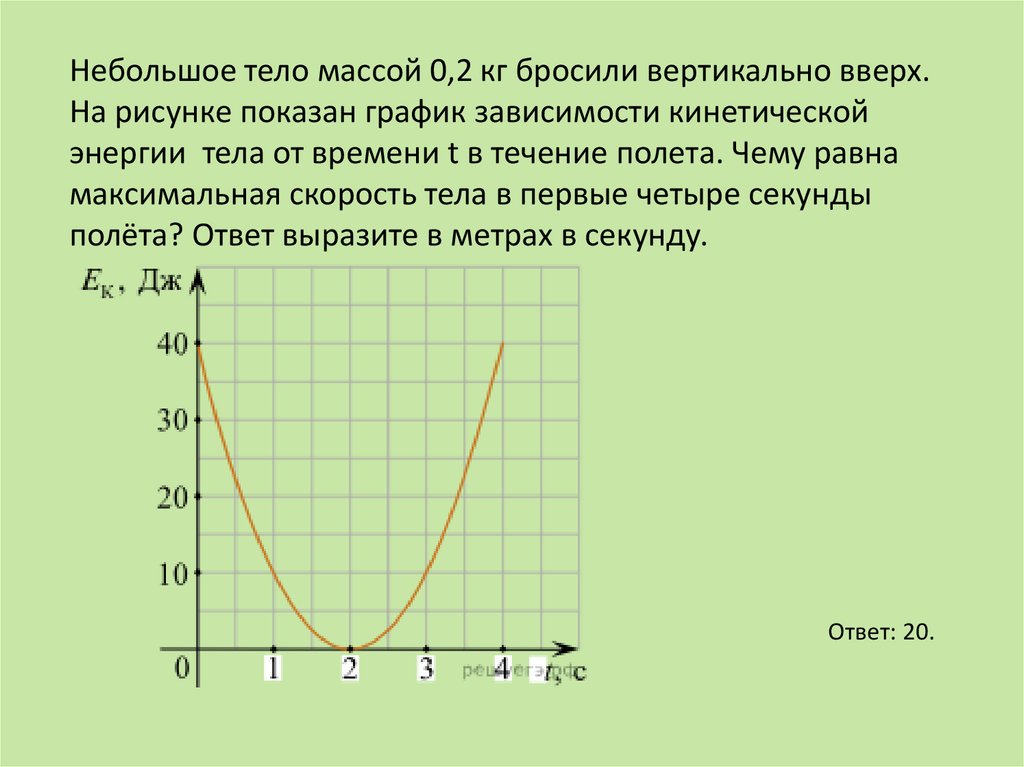
Небольшое тело массой 0,2 кг бросили вертикально вверх.
На рисунке показан график зависимости кинетической
энергии тела от времени t в течение полета. Чему равна
максимальная скорость тела в первые четыре секунды
полёта? Ответ выразите в метрах в секунду.
Ответ: 20.

5.

Мальчик бросил камень массой 100 г под углом к горизонту
из точки A. На рисунке в некотором масштабе изображена
траектория ABC полета камня. Сопротивление воздуха
пренебрежимо мало. В точке B траектории модуль скорости
камня был равен 8 м/с. Какую кинетическую энергию имел
камень в точке C? (Ответ дайте в джоулях.)
Ответ: 9,2

6.

• При выполнении трюка «Летающий велосипедист»
гонщик движется по гладкому трамплину под действием
силы тяжести, начиная движение из состояния покоя с
высоты Н (см. рис.). На краю трамплина скорость гонщика
направлена под углом α = 60° к горизонту. Пролетев по
воздуху, он приземляется на горизонтальный стол,
находящийся на той же высоте, что и край трамплина.
Какова дальность полёта гонщика?

7.

• После толчка льдинка закатилась в яму с гладкими
стенками, в которой она может двигаться практически без
трения. На рисунке приведен график зависимости энергии
взаимодействия льдинки с Землей от её координаты в
яме. В некоторый момент времени льдинка находилась в
точке А с координатой 10 см и двигалась влево, имея
кинетическую энергию, равную 2 Дж. Сможет ли льдинка
выскользнуть из ямы? Ответ поясните, указав, какие
физические закономерности вы использовали для
объяснения.

8.

• Клин массой M с углом α при основании закреплён на
шероховатой горизонтальной плоскости (см. рис.). На вершине
клина, на высоте H над плоскостью находится маленький
брусок массой m, коэффициент трения которого о верхнюю
половину наклонной поверхности клина и о шероховатую
горизонтальную плоскость равен
Нижняя половина наклонной поверхности клина гладкая. Брусок
отпускают без начальной скорости, он скатывается по клину и
далее скользит по шероховатой плоскости и останавливается на
некотором расстоянии L по горизонтали от своего начального
положения. Найдите это расстояние L, если в точке перехода с
клина на плоскость есть гладкое закругление, так что скорость
бруска при переходе с клина на плоскость не уменьшается.
Ответ: