Похожие презентации:
Производная давления. Прямой анализ с помощью производной. Знакомство с программным модулем «Saphir»
1. План 1. Производная давления 2. Прямой анализ с помощью производной 3. Знакомство с программным модулем «Saphir»
План1. Производная давления
2. Прямой анализ с помощью производной
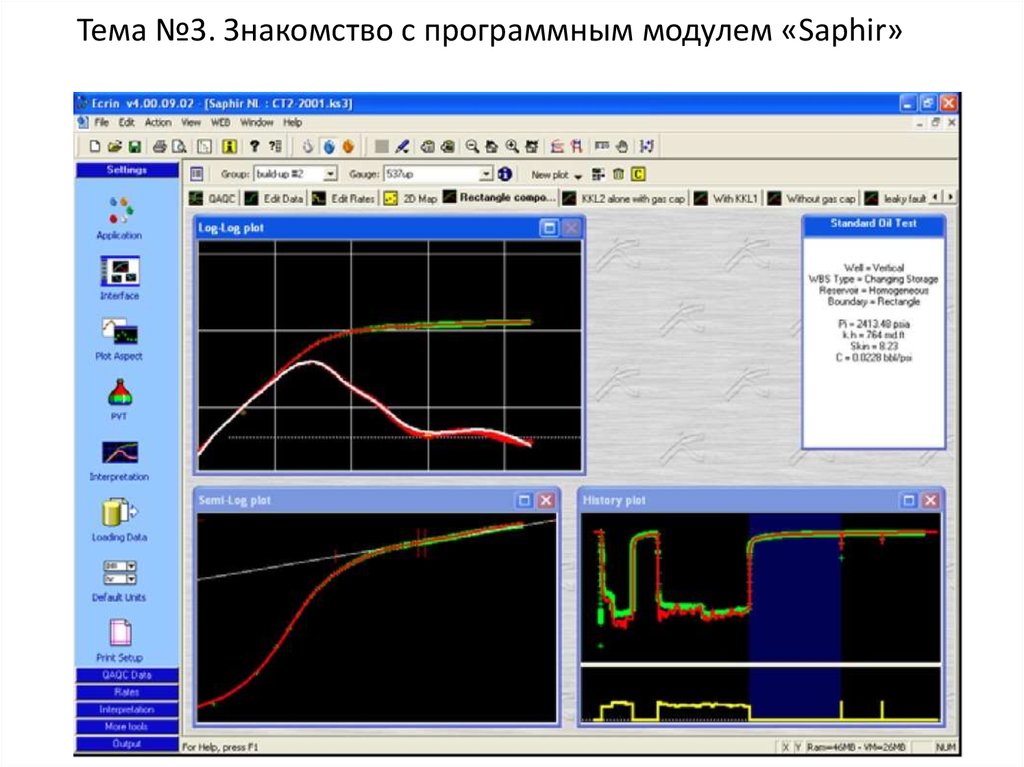
3. Знакомство с программным модулем «Saphir»
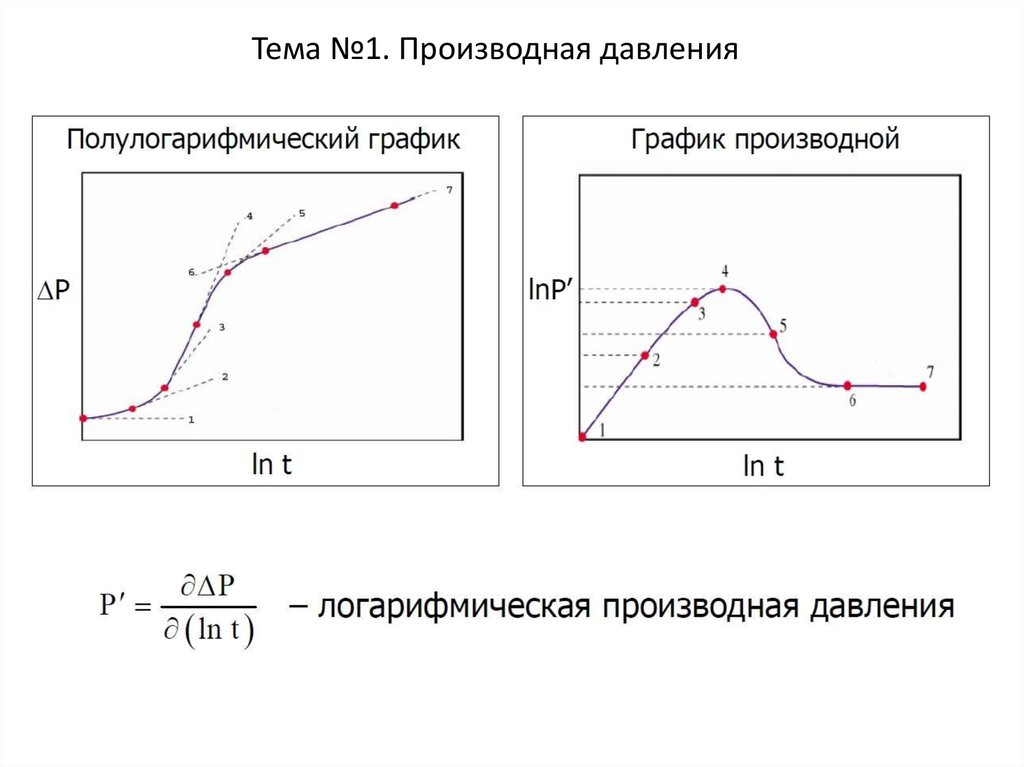
2. Тема №1. Производная давления
3.
4.
5.
6.
7.
8.
9.
10.
• Процесс дифференцирования может датьочень зашумленную производную, поэтому
необходимо сглаживать данные. Существует
множество алгоритмов сглаживания данных. В
основе этих алгоритмов лежит понятие
интервала дифференцирования δ.
• Для того, чтобы найти значение производной в
точке t i , рассматривают интервал ሾlnሺt i −
11.
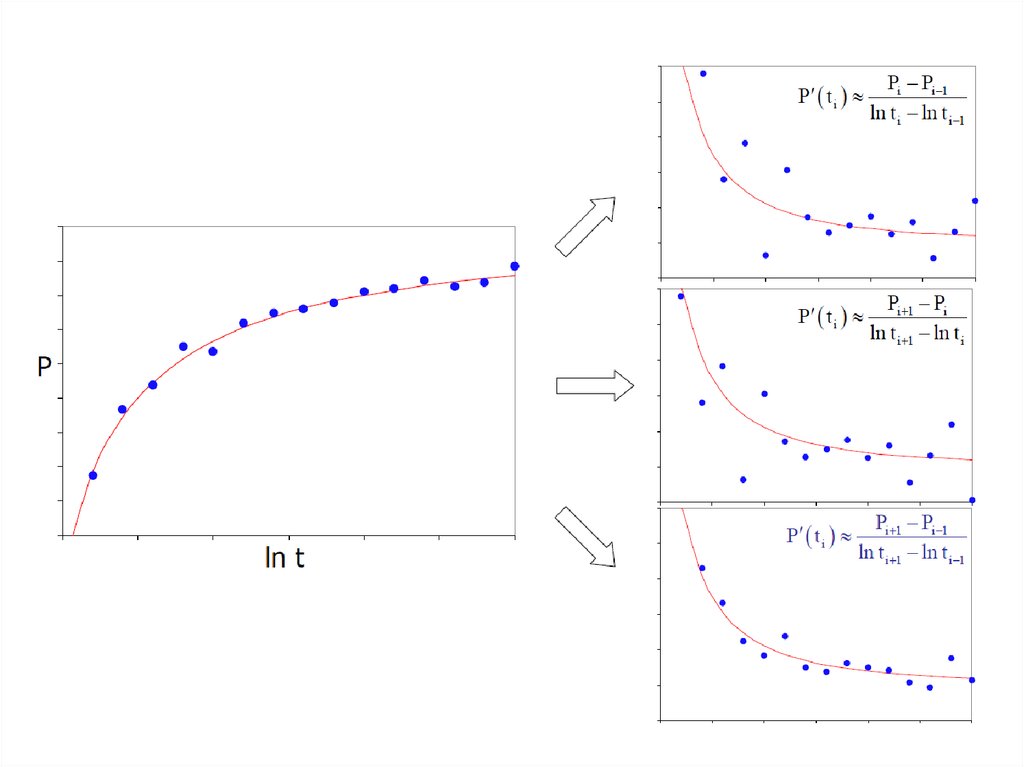
К наиболее распространенным алгоритмам сглаживанияотносятся:
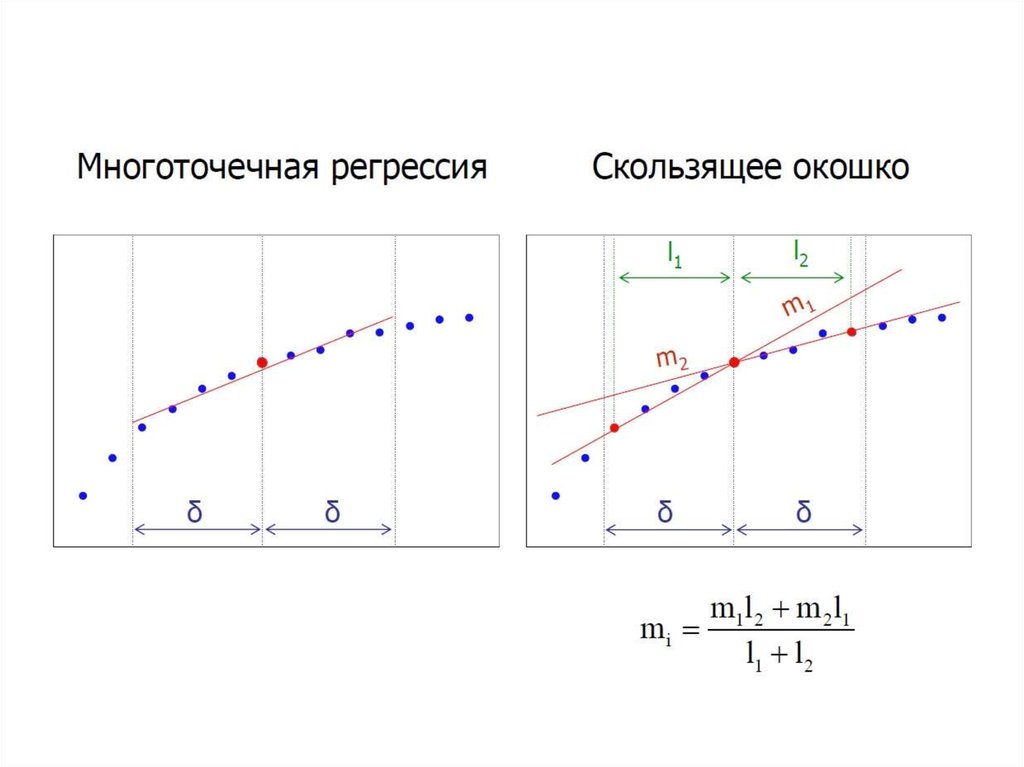
• Многоточечная регрессия.
Через точки, попавшие в интервал ln t i − δ ; ln t i + δ ,
проводится регрессионная прямая. Наклон этой прямой линии
есть значение производной в точке t i .
• Скользящее окошко.
Через точки lnt i − δ и lnt i проводят прямую линию,
определяют ее наклон m1 . Через точки lnt i и lnt i + δ проводят
прямую линию, определяют ее наклон m2 . Производная в точке t i
есть среднее арифметическое наклонов m1 и m2 . В общем случае,
если точки расположены неравномерно по времени, прямые
строятся через точку t i и самые дальние от нее точки, попадающие
в интервал ln t i − δ ; ln t i + δ . В данном случае производная
равна средневзвешенному наклонов m1 и m2 .
m1 l2 + m2 l1
mi =
l1 + l2
12.
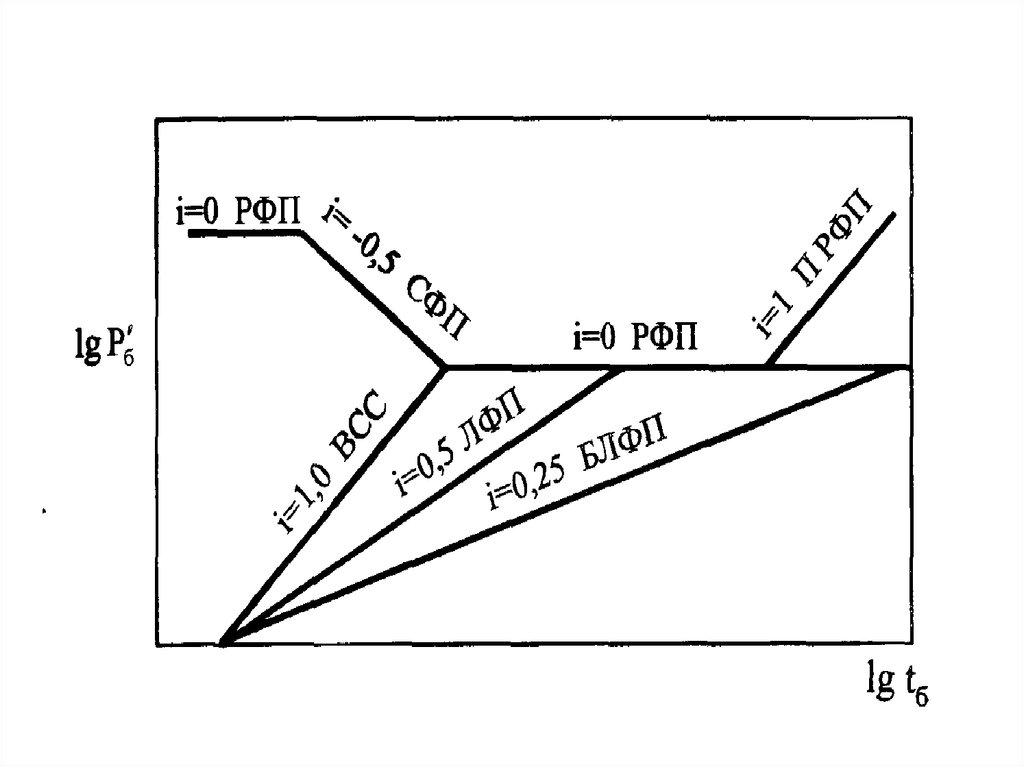
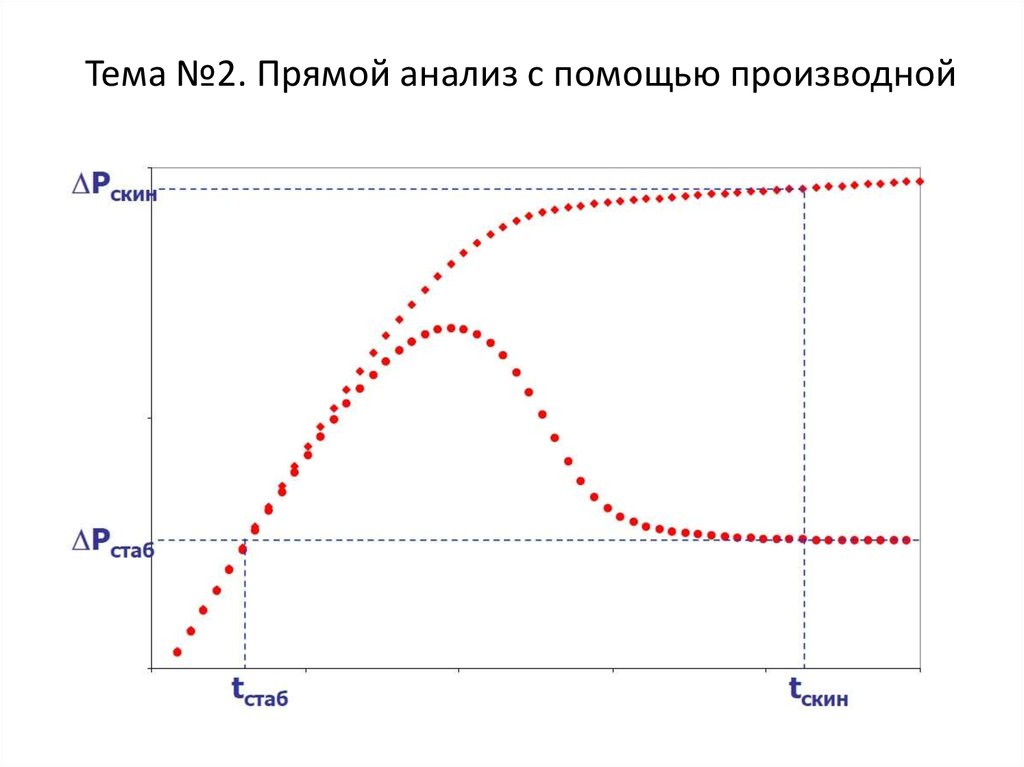
Тема №2. Прямой анализ с помощью производной13.
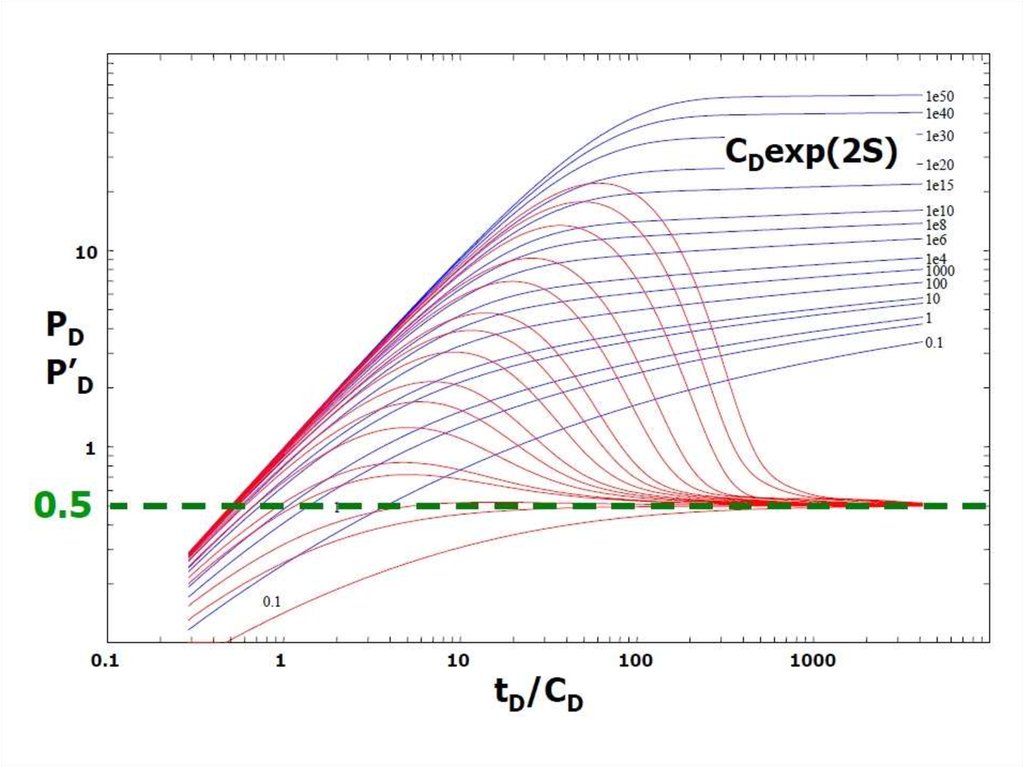
С момента достижения радиального притока производная давлениястабилизируется, а безразмерное значение давления равно 0,5. Отсюда:







 Промышленность
Промышленность








