Геометриядә охшашлыклар

1.

2.

Геометриядә охшашлыклар
Охшаш өчпочмаклар һәм аны мәсьәләләр
чишүдә куллану
2017 г.

3.

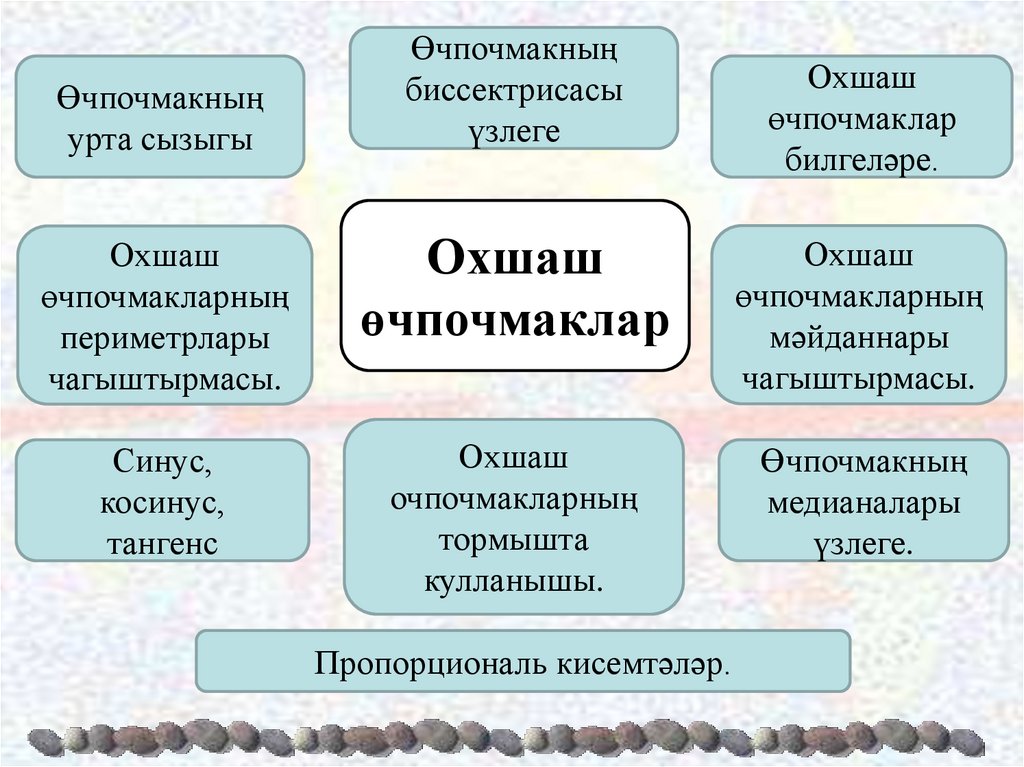
Өчпочмакның
урта сызыгы
Өчпочмакның
биссектрисасы
үзлеге
Охшаш
өчпочмаклар
билгеләре.
Охшаш
өчпочмакларның
периметрлары
чагыштырмасы.
Охшаш
өчпочмаклар
Охшаш
өчпочмакларның
мәйданнары
чагыштырмасы.
Синус,
косинус,
тангенс
Охшаш
очпочмакларның
тормышта
кулланышы.
Өчпочмакның
медианалары
үзлеге.
Пропорциональ кисемтәләр.

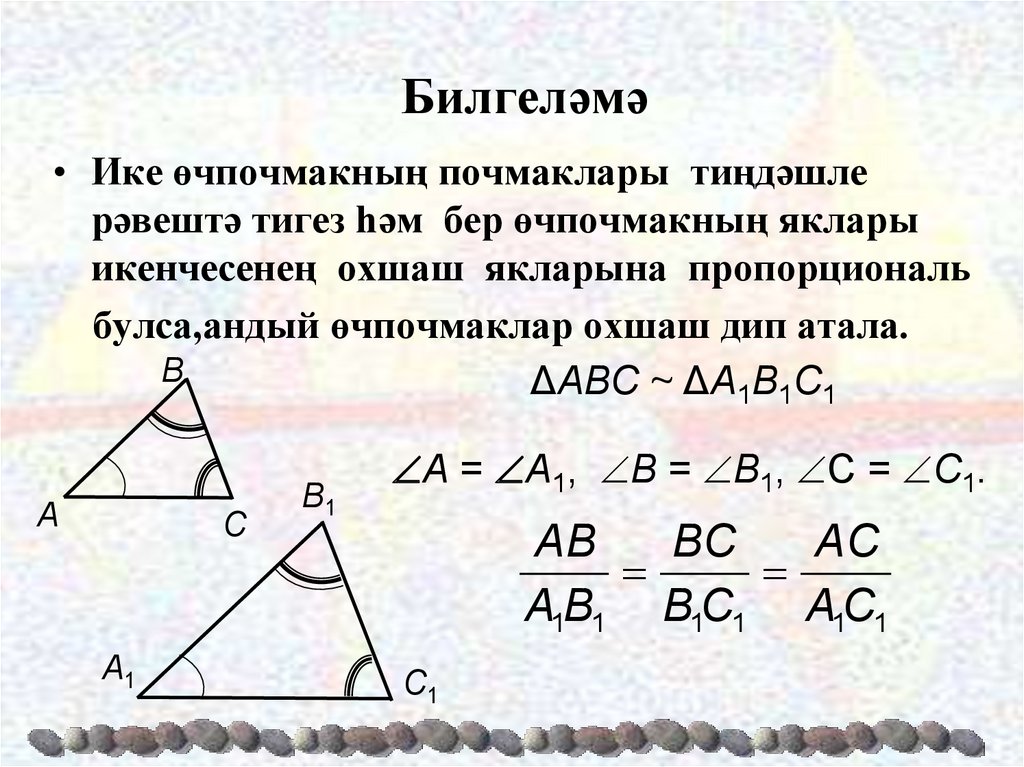
4. Билгеләмә

• Ике өчпочмакның почмаклары тиңдәшле
рәвештә тигез һәм бер өчпочмакның яклары
икенчесенең охшаш якларына пропорциональ
булса,андый өчпочмаклар охшаш дип атала.
Β
ΔAΒC ~ ΔA1Β1C1
A
C
A1
Β1
A = A1, Β = Β1, C = C1.
AB
BC
AC
A1B1 B1C1 A1C1
C1

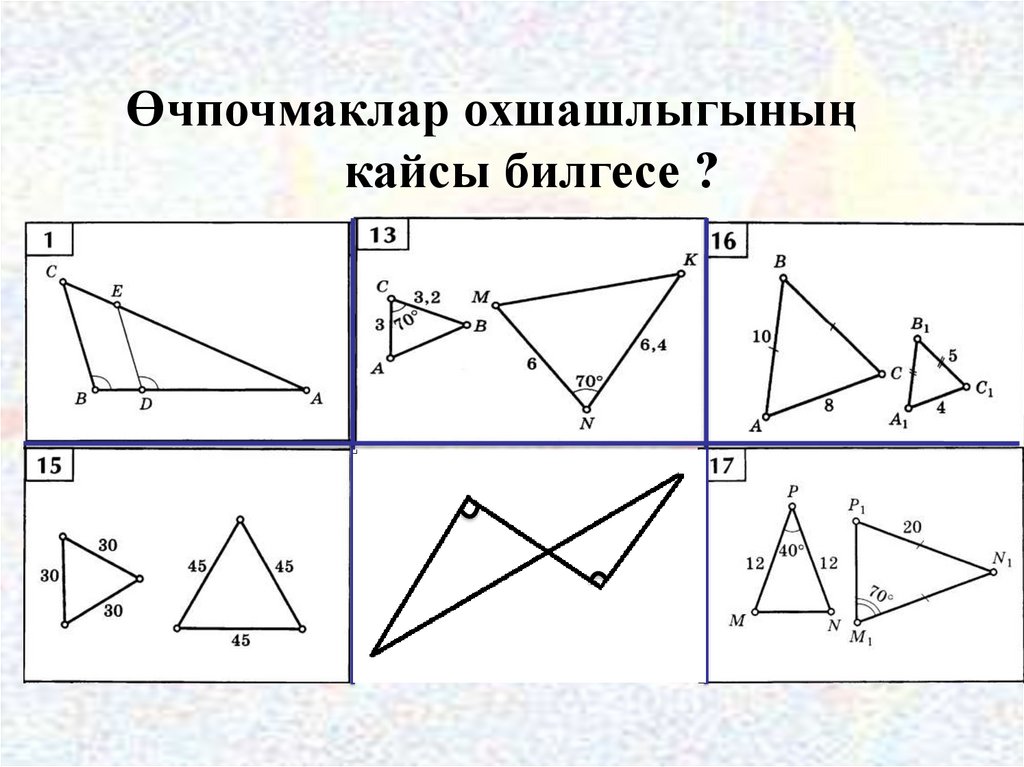
5.

Өчпочмаклар охшашлыгының
кайсы билгесе ?

6. Өчпочмакларның охшашлык билгеләре

Өчпочмаклар охшашлыгының 1 билгесе.
(ике почмак тигез)
Өчпочмаклар охшашлыгының 2 билгесе.
(ике як пропорциональ, арадагы почмак тигез)
Өчпочмаклар охшашлыгының 3 билгесе.
(өч якның пропорциональлеге)

7. Телдән исәпләү

8.

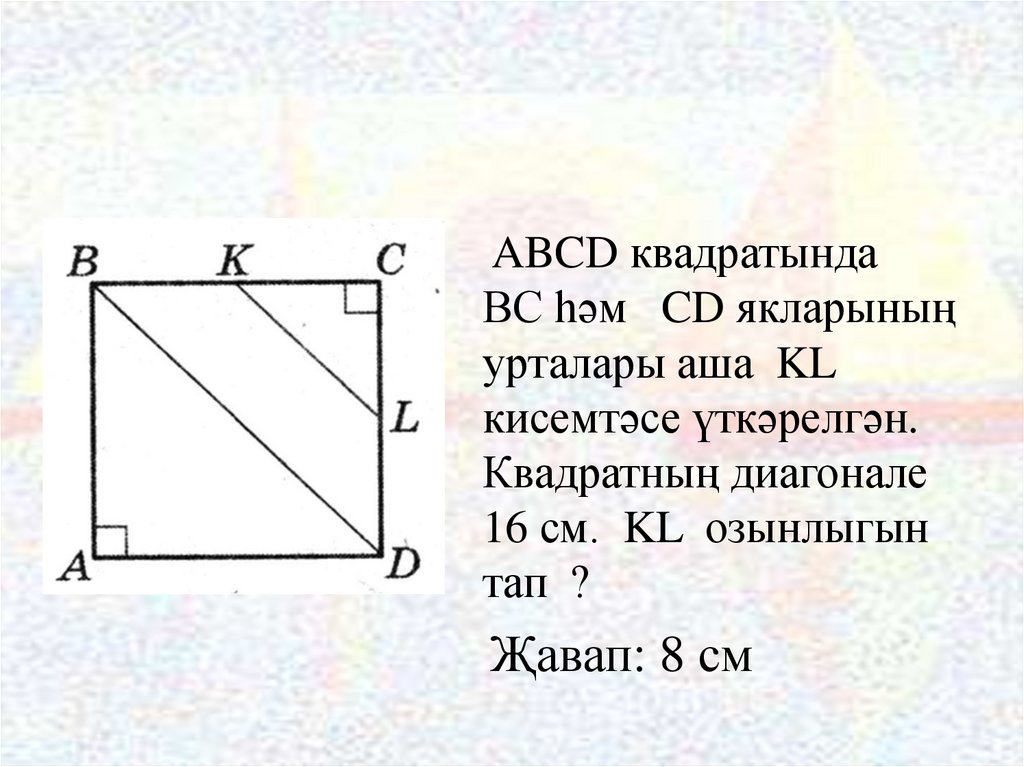
ABCD квадратында
ВС һәм CD якларының
урталары аша KL
кисемтәсе үткәрелгән.
Квадратның диагонале
16 см. KL озынлыгын
тап ?
Җавап: 8 см

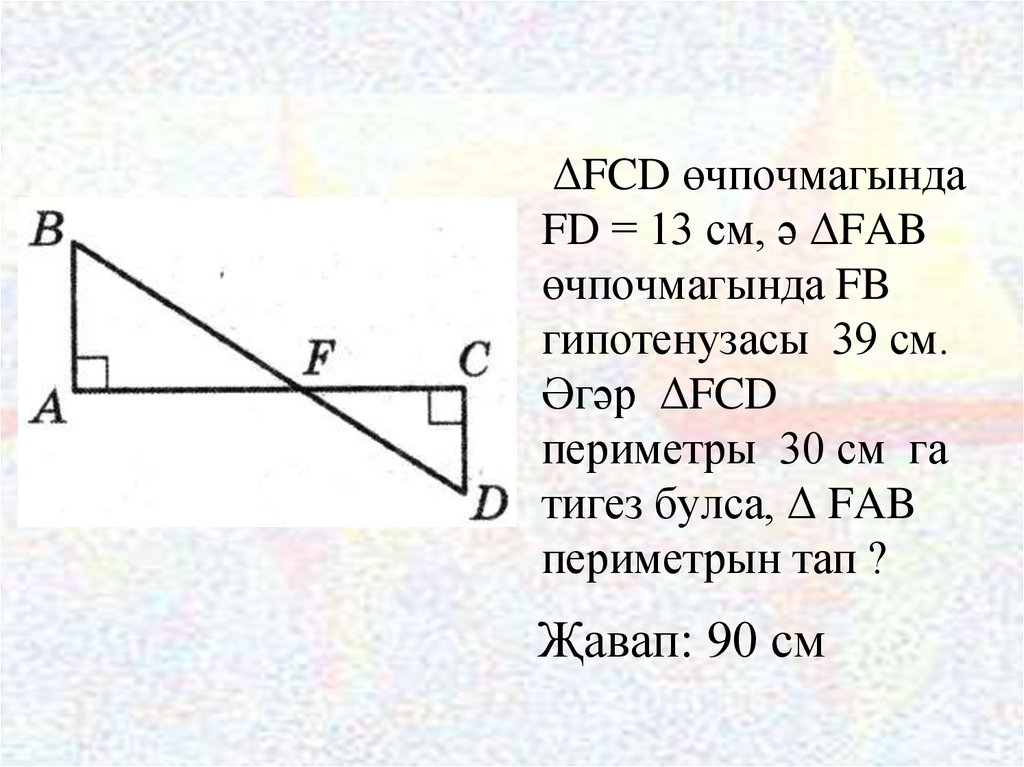
9.

ΔFCD өчпочмагында
FD = 13 см, ә ΔFAB
өчпочмагында FB
гипотенузасы 39 см.
Әгәр ΔFCD
периметры 30 см га
тигез булса, Δ FAB
периметрын тап ?
Җавап: 90 см

10.

ΔABC ~ ΔA1B1C1 ,
AB : A1B1 = k = 4
SΔABC= 48 м2.
A1B1C1 өчпочмагының мәйданын тап?
Җавап: 3 м2

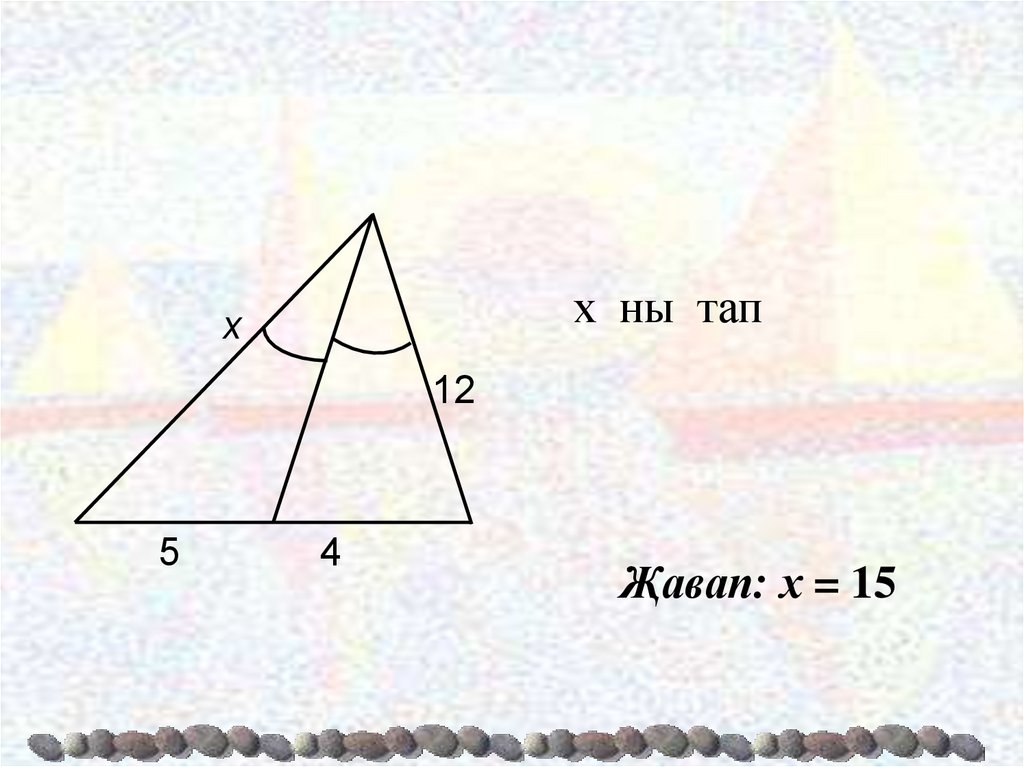
11.

х ны тап
х
12
5
4
Җавап: х = 15

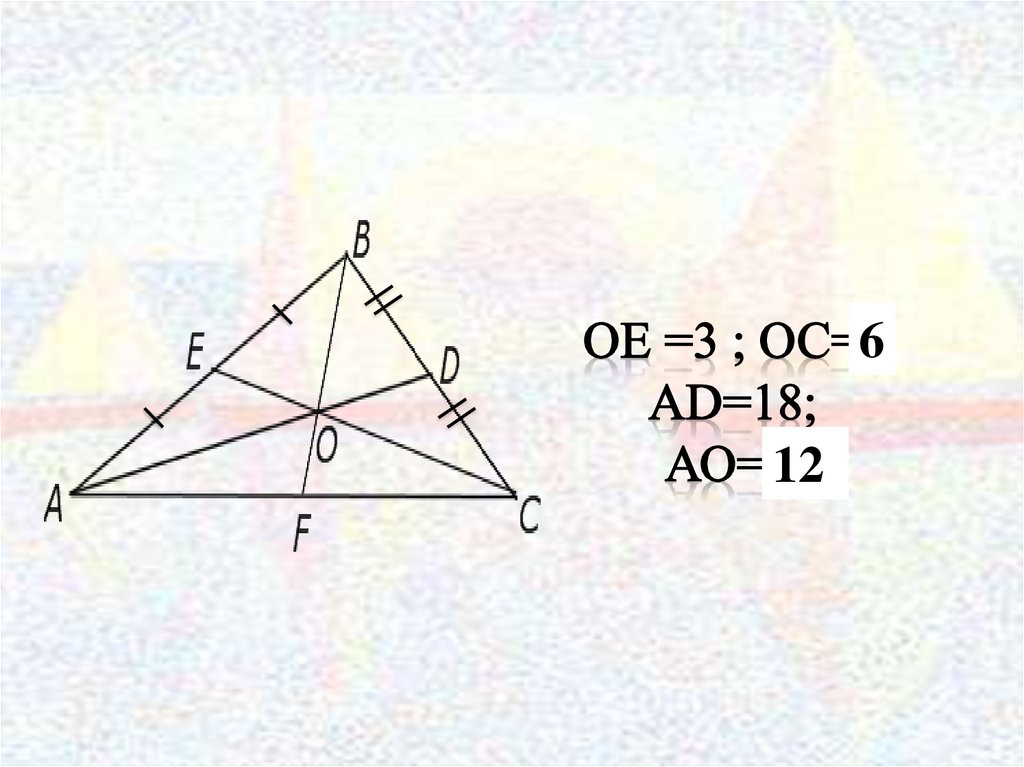
12.

6
12

13.

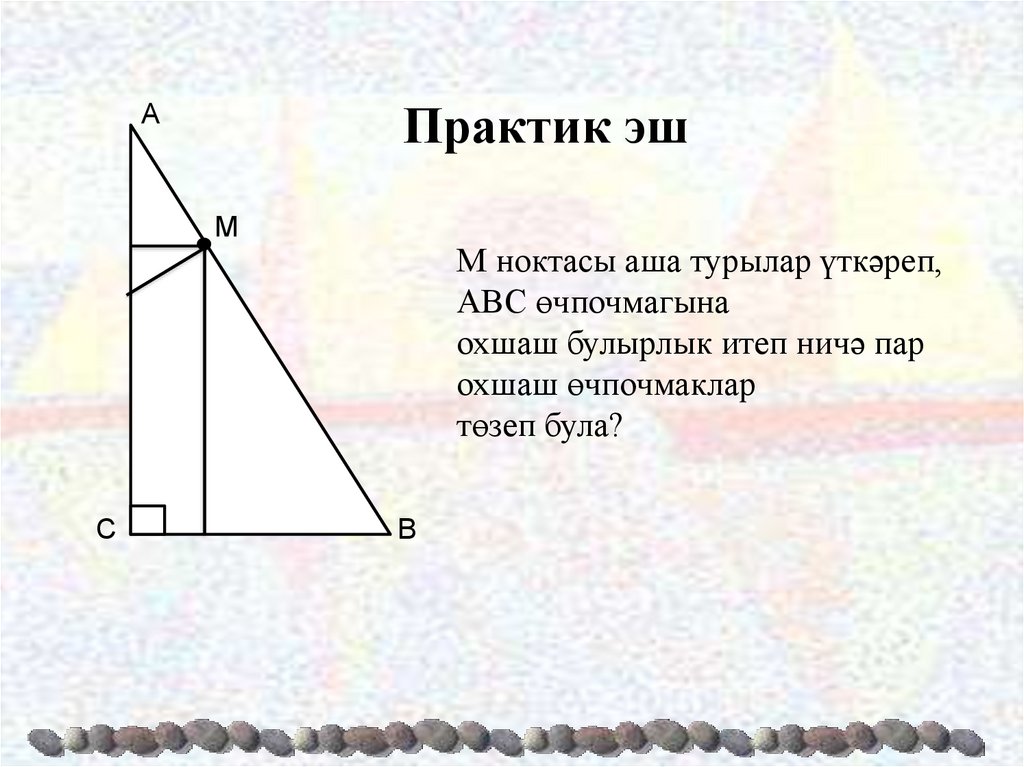
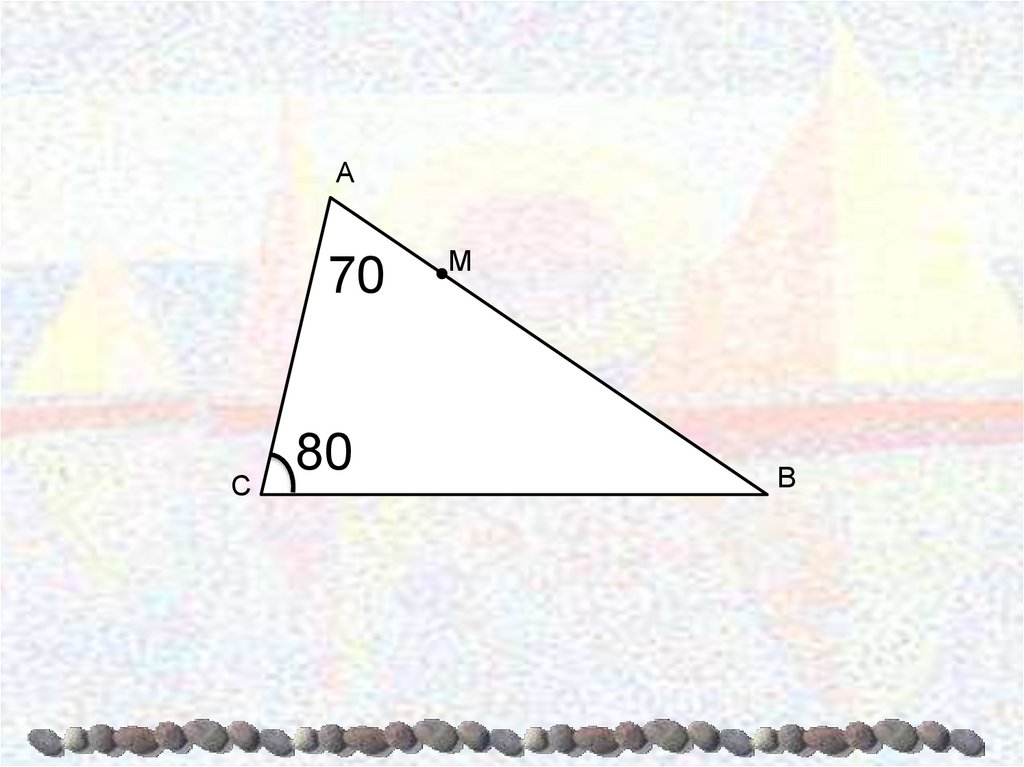
Практик эш
А
М
С
М ноктасы аша турылар үткәреп,
АВС өчпочмагына
охшаш булырлык итеп ничә пар
охшаш өчпочмаклар
төзеп була?
В

14.

А
70
С
80
М
В

15. ОГЭ дан эшләр

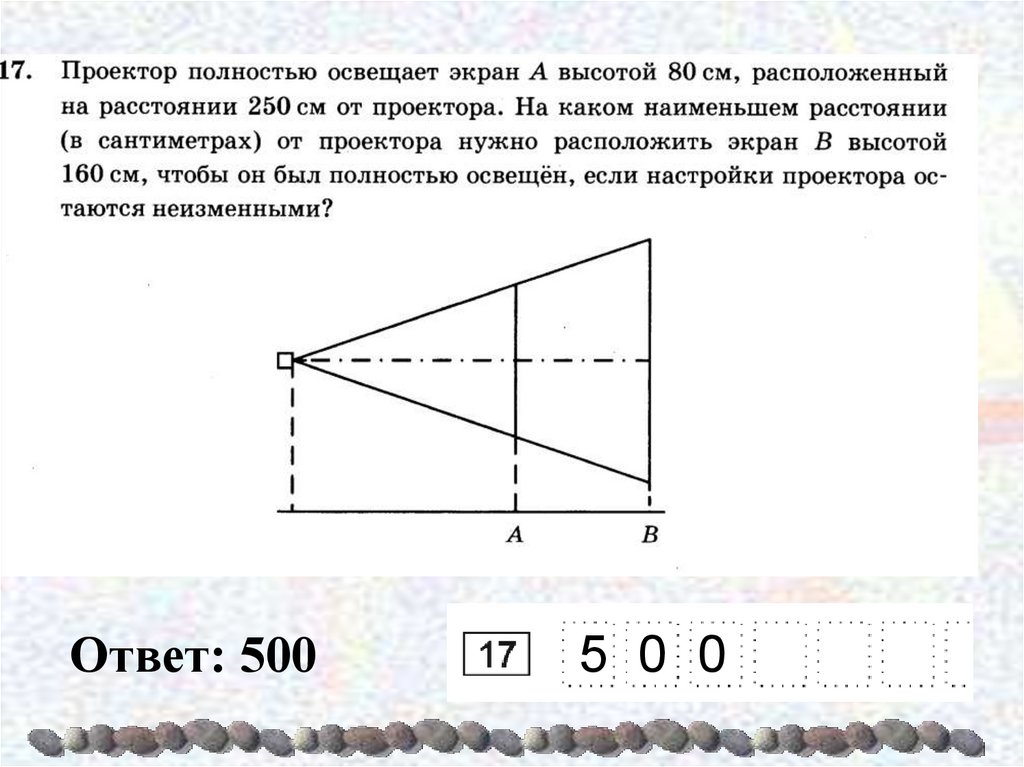
16.

Ответ: 500
5 0 0

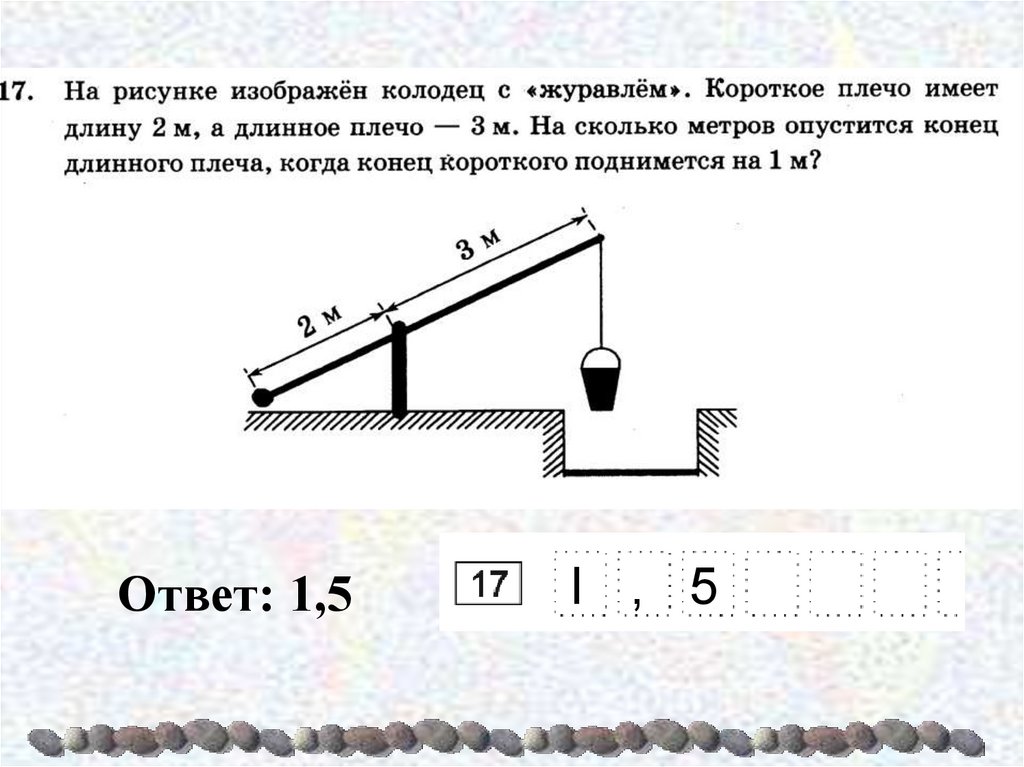
17.

Ответ: 1,5
l , 5

18.

Баганага җирдән 10 м биеклектә фонарь эленгән. Кеше
баганадан 12,3 м ераклыкта басып тора. Әгәр кешенең җиргә
төшкән күләгәсе 2,7 м булса, аның буеның озынлыгын табыгыз
(метрларда).
Җавап: 1,8
l , 8

19.

20.

21. Какие из следующих утверждений верны?

1. Любые два равносторонних треугольника подобны.
2. Если два угла одного треугольника
соответственно пропорциональны двум углам
другого треугольника, то такие треугольники
подобны.
3. Если два треугольника подобны, то их
сходственные стороны пропорциональны.
l 3

22. Какие из следующих утверждений НЕ верны?

1. Если две стороны одного треугольника
пропорциональны сходственным сторонам другого
треугольника, и углы, заключенные между этими
сторонами равны, то такие треугольники подобны.
2. Любые два равнобедренных треугольника
подобны.
3. Если угол одного треугольника равен углу другого
треугольника, то такие треугольники подобны.
2 3

23.

Ответ: 23
Ответ:4
Ответ: 5,5

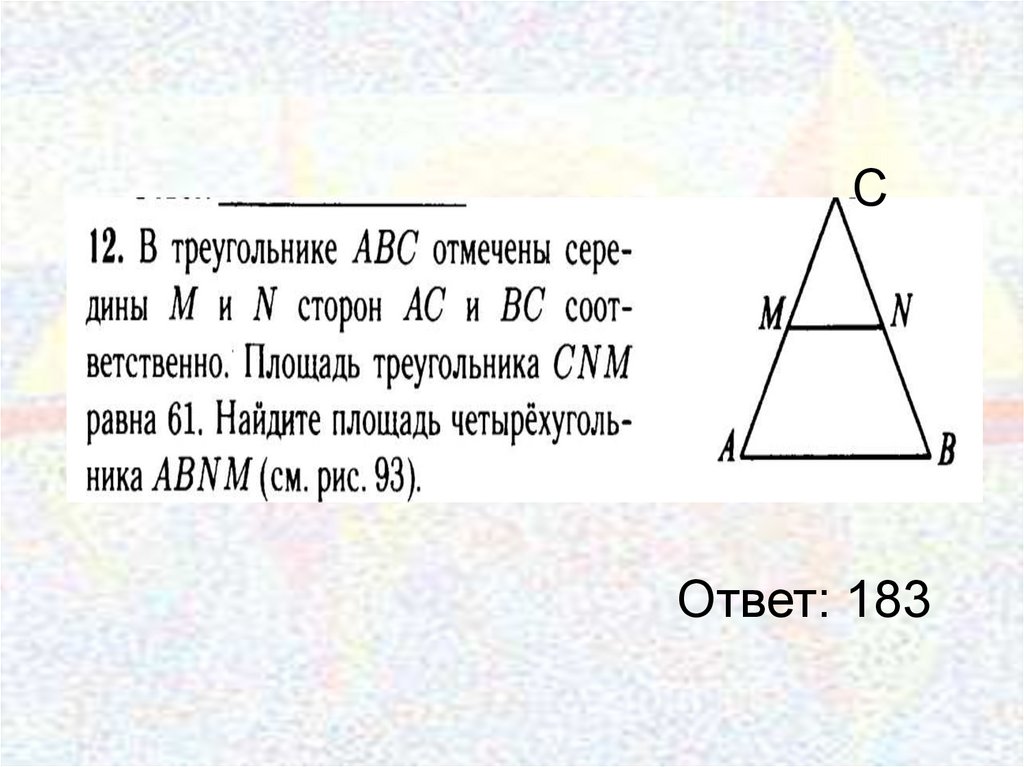
24.

С
Ответ: 183

25.

Ответ: 0,6

26.

Ответ: 10