Решение типовых задач алгебры и анализа

1.

1

2.

Задачи линейной алгебры
В системе MATLAB для решения задачи линейной алгебры –
нахождение корней систем линейных уравнений – предусмотрены знаки
операций / и \ .
Чтобы решить систему линейных уравнений:
которую обычно кратко записывают в виде:
Ax = B
где A – заданная квадратная матрица (размером NxN) коэффициентов
при неизвестных , a B – заданный вектор-столбец длины N свободных
членов , достаточно применить операцию \ и вычислить выражение
x=A\B.
Операция \, называется левым делением матриц и, будучи
примененная к матрицам A и B в виде A\B, эквивалентна вычислению
выражения inv(A)*B. Здесь под inv(A) понимается вычисление
матрицы, обратной к матрице A.
Для вычисления определителя квадратной матрицы А
предназначена встроенная функция det(A).
2

3.

Задачи линейной алгебры
3

4.

Нахождение нулей функций
Функция fzero позволяет приближенно вычислить корень уравнения на
некотором интервале или ближайший к заданному начальному приближению. В
простейшем варианте fzero вызывается с двумя входными и одним выходным
аргументом x = fzero(func_name, x0), где func_name – имя файл-функции,
вычисляющей левую часть уравнения, x0 — начальное приближение к корню, х –
найденное приближенное значение корня. Решим, например, на отрезке [-5, 5]
уравнение:
Перед нахождением корней полезно построить график функции,
входящей в левую часть уравнения. Для получения графика можно прибегнуть к
plot, но все равно понадобится запрограммировать функцию, поэтому имеет
смысл воспользоваться fplot, которая к тому же позволяет получить более
точный график по сравнению с plot. Текст требуемой файл-функции:
function y = myf(x)
y = sin(x) - x.^2.*cos(x);
Теперь построим график функции myf, используя fplot, и нанесем сетку.
>> fplot('myf', [-5 5])
>> grid on
4

5.

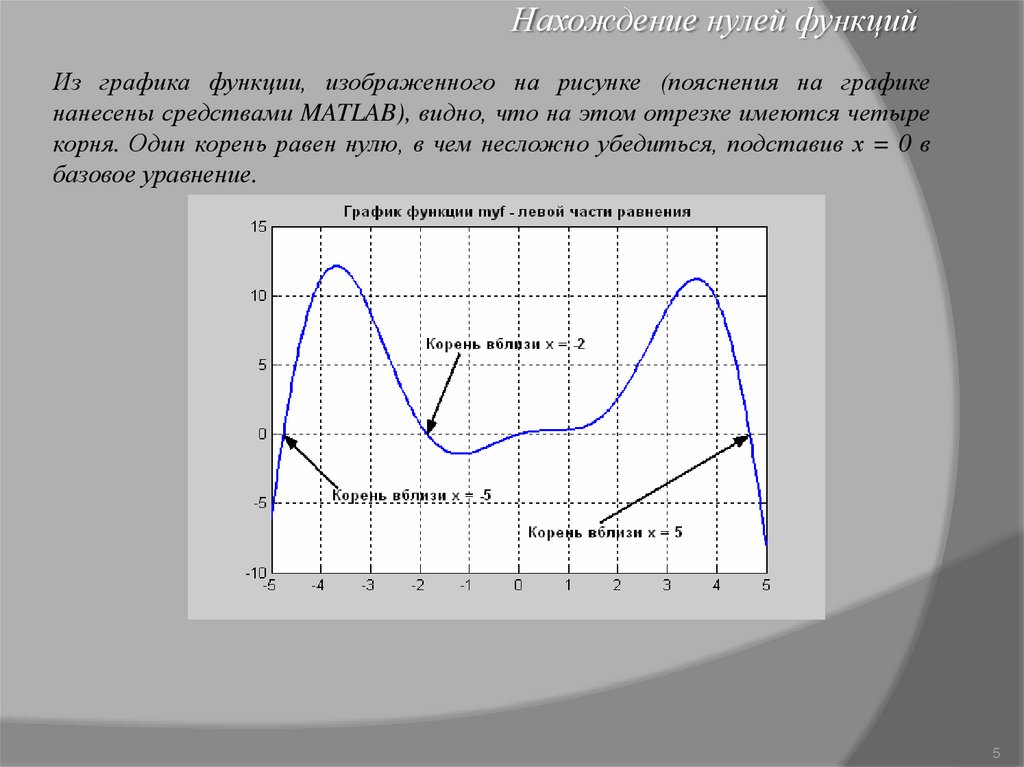
Нахождение нулей функций
Из графика функции, изображенного на рисунке (пояснения на графике
нанесены средствами MATLAB), видно, что на этом отрезке имеются четыре
корня. Один корень равен нулю, в чем несложно убедиться, подставив х = 0 в
базовое уравнение.
5

6.

Нахождение нулей функций
Уточним значение корня, расположенного вблизи х = - 5, при помощи fzero:
>> xl = fzero('myf', -5)
xl =
-4.7566
Итак, приближенное значение корня равно -4.7566. При указании
начального приближения к корню алгоритм fzero автоматически отделяет корень,
т.е. вблизи заданного начального приближения находится отрезок, содержащий
корень. Проверим ответ, вычислив значение функции myf в точке x1:
>> myf(xl)
ans =
2.6645e-015
Гарантированная точность приближенного значения определяется
расстоянием до его истинного значения или (что фактически то же самое)
количеством верных значащих цифр. Как задать точности вычислений мы
рассмотрим позже, когда будем рассматривать вопрос управление ходом
вычислений.
6

7.

Нахождение нулей функций
Вместо начального приближения вторым параметром fzero можно задать
интервал, на котором следует найти корень:
>> x2 = fzero('myf',[-3 -1])
x2 =
-1.8539
На границах указываемого интервала функция должна принимать значения
разных знаков, иначе выведется сообщение об ошибке!
В качестве исследуемой функции может выступать и встроенная математическая
функция, например:
>> x=fzero('cos', 1)
x=
1.5708
Формат вызова функции fzero, имеет вид:
x = fzero(func_name, x0)
Необходимо отметить, что имя функции func_name, задающее исходное выражения,
для fzero (это также справедливо для большинства других функций MATLAB, таких
как fplot, fminbnd и др.) можно задавать как:
• как имя m-файла (в апострофах и без расширения m) – 'MyFunc1', 'cos'
• как указатель на функцию – @MyFunc1, @cos
• или как формула с одним неизвестным x, которую необходимо заключить в
апострофах – 'cos(x)+x^3-x', 'cos(x)'
7

8.

Вычисление всех корней полинома
Полином в MATLAB задается вектором его
коэффициентов, например, для определения
полинома следует использовать команду:
>> p = [1, 0, 3.2, -5.2, 0, 0.5, 1, -3];
Число элементов вектора, т. е. число коэффициентов полинома, всегда на
единицу больше его степени, нулевые коэффициенты должны содержаться в векторе.
Функция polyval предназначена для вычисления значения полинома от некоторого
аргумента:
>> polyval(p,1)
ans =
-2.5000
Нахождение всех корней полиномов осуществляется при помощи функции roots, в
качестве аргумента которой указывается вектор с коэффициентами полинома. Функция
roots возвращает вектор корней полинома, в том числе и комплексных:
>> r = roots(p)
r=
-0.5668 + 2.0698i
-0.5668 - 2.0698i
-0.6305 + 0.5534i
-0.6305 - 0.5534i
1.2149
0.5898 + 0.6435i
0.5898 - 0.6435i
8

9.

Поиск минимума функций
Функции одной вещественной переменной.
Поиск локального минимума функции одной переменной на некотором отрезке
осуществляется при помощи fminbnd, использование которой схоже с fzero. Найдем
локальные минимумы функции:
на отрезке [-1.5,1.5]. Требуется предварительно создать соответствующую файлфункцию, назвав ее, к примеру ftest, или ввести inline. Приведем пример
использования функции inline:
>> ftest=inline('exp(x.^2)+sin(3*pi*x)');
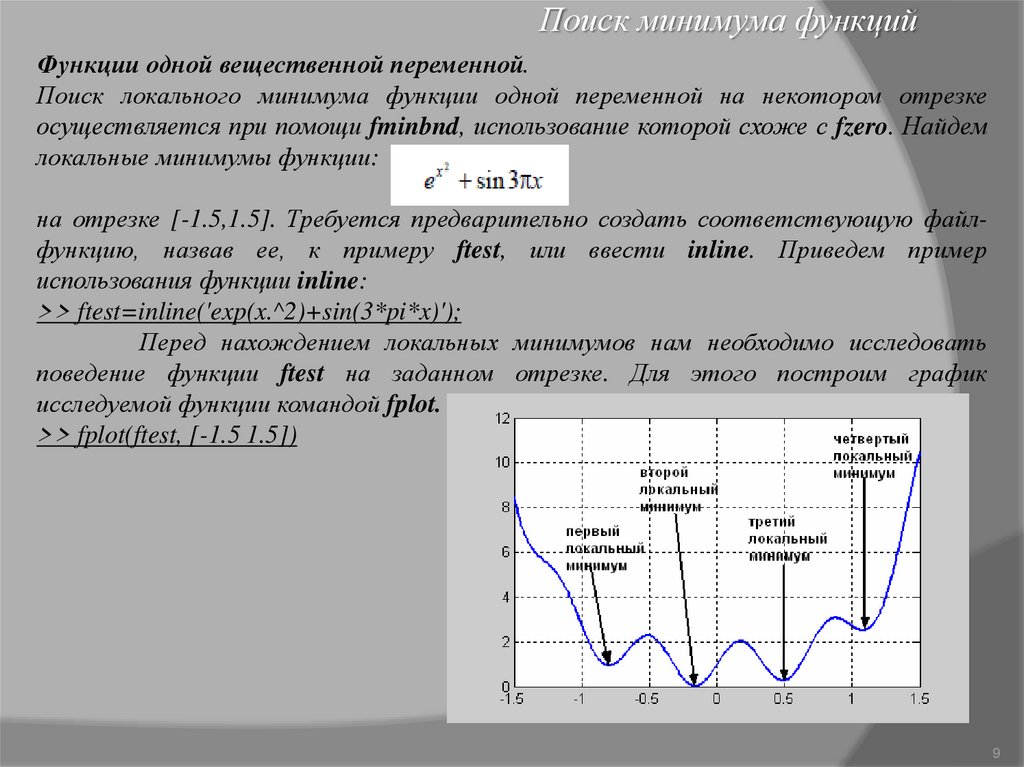
Перед нахождением локальных минимумов нам необходимо исследовать
поведение функции ftest на заданном отрезке. Для этого построим график
исследуемой функции командой fplot.
>> fplot(ftest, [-1.5 1.5])
9

10.

Поиск минимума функций
Вычислим значение х, при котором достигается второй локальный
минимум, задав первым аргументом fminbnd имя файл-функции или указатель
на нее, а вторым и третьим – границы отрезка, на котором ищется локальный
минимум.
>> x2 = fminbnd(ftest, -0.5, 0)
x2 =
-0.1629
Для одновременного вычисления значения функции в точке минимума
следует вызвать fminbnd с двумя аргументами:
>> [x2,f] = fminbnd(ftest, -0.5, 0)
x2 =
-0.1629
f=
0.0275
10

11.

Поиск минимума функций
Функции нескольких переменных.
Минимизация функции нескольких переменных является более сложной задачей по
сравнению с минимизацией функции одной переменной, однако комбинированный
адаптивный алгоритм функции fminsearch позволяет во многих случаях успешно
решить эту задачу. Функция fminsearch требует указания начального приближения
для искомой точки минимума, которое в случае функции одной переменной должно
быть числом, а для функции нескольких переменных – вектором.
Рассмотрим теперь минимизацию функций нескольких переменных на примере
функции двух переменных:
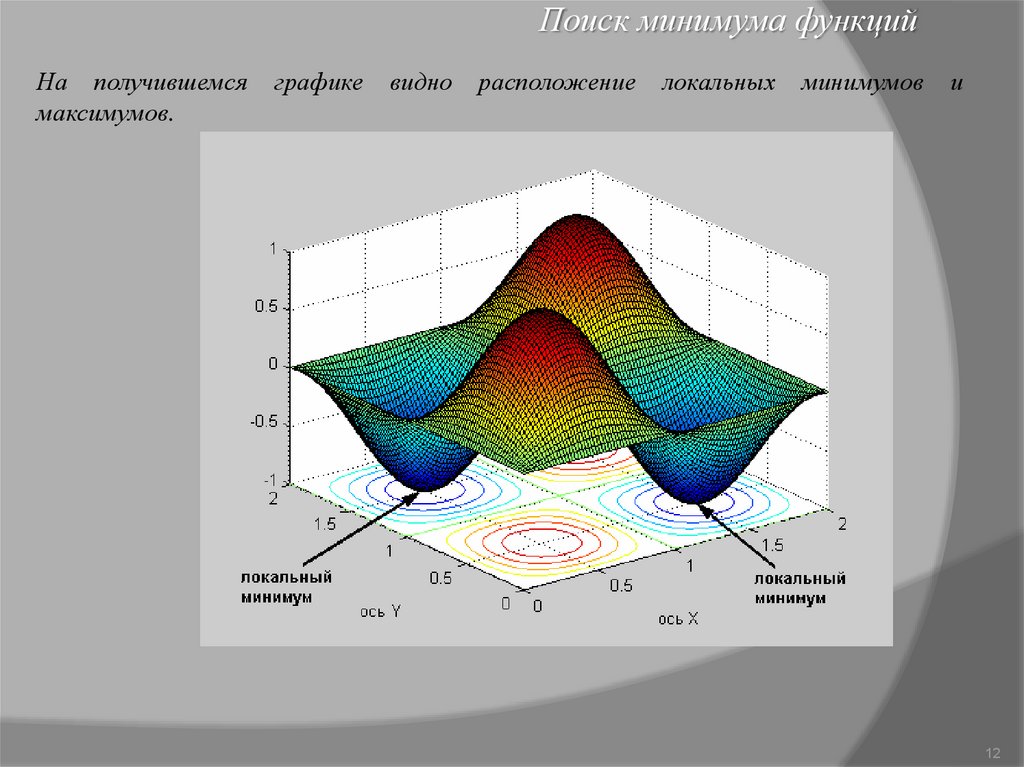
Для анализа поведения функции, сначала построим трехмерный график (сетчатый,
с функциональной заливкой), с контурными линиями, используя функцию surfc:
[X, Y] = meshgrid(0:0.02:2);
Z = sin(pi*X).*sin(pi*Y);
surfc(X,Y,Z)
11

12.

Поиск минимума функций
На получившемся
максимумов.
графике
видно
расположение
локальных
минимумов
и
12

13.

Поиск минимума функций
Перед применением fminsearch необходимо создать файл-функцию,
вычисляющую значения искомой функции, причем аргументом файл-функции должен
быть вектор, первый элемент которого соответствует переменной х, а второй – у.
Текст требуемой файл-функции приведен ниже:
function f = ftest2(v)
x = v(1);
y = v(2);
f = sin(pi*x).*sin(pi*y);
Теперь для нахождения локального минимума вызовите fminsearch с двумя
входными аргументами – именем файл-функции и начальным приближением и
выходным аргументом –вектором с координатами искомой точки минимума:
>> M = fminsearch('ftest2', [1.4, 0.6])
M=
1.5000 0.5000
Для получения не только вектора с координатами точки минимума, но и значения
функции следует вызвать fminsearch с двумя выходными аргументами:
>> [M,F] = fminsearch('ftest2', [1.4, 0.6])
M=
1.5000 0.5000
F=
-1.0000
13

14.

Управление ходом вычислением
Функции fzero, fminbnd и fminsearch допускают определение
дополнительных параметров для управления вычислительным процессом и контроля
за ним. Формат вызова:
fzero(fname, x0, options)
fminbnd(fname, x1, x2, options)
fminsearch(fname, x0, options)
Параметры задаются в управляющей структуре, которую мы будем
называть options, как в справочной системе MATLAB, хотя имя может быть
произвольным. Перед вызовом вычислительных функций следует предварительно
сформировать переменную options в соответствии с характером требуемого
контроля, воспользовавшись функцией optimset. Переменная options на самом деле
является структурой.
Приступим к формированию структуры options на примере минимизации
функции одной переменной при помощи fminbnd. Для изменения точности следует
сформировать структуру options, указав требуемую точность (например 10-9) по
аргументу при помощи параметра TolX:
>> format long
>> options = optimset('TolX', 1.0e-09);
>> x2 = fminbnd(ftest, -0.5, 0, options)
x2 =
-0.16289942841268
14

15.

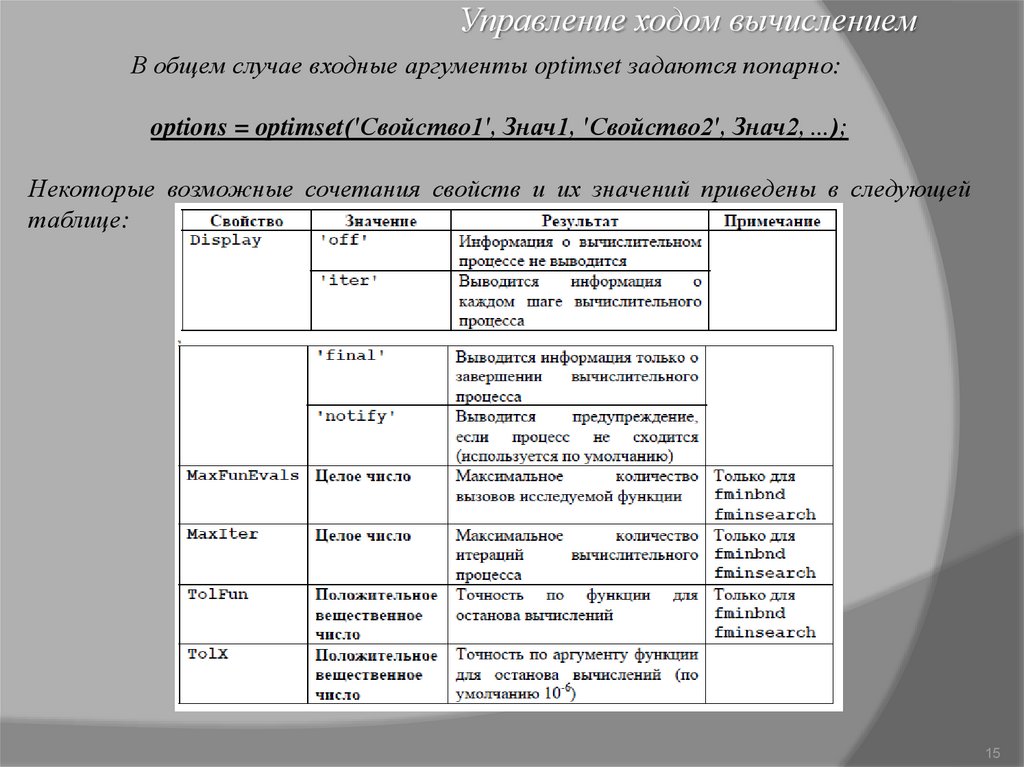
Управление ходом вычислением
В общем случае входные аргументы optimset задаются попарно:
options = optimset('Свойство1', Знач1, 'Свойство2', Знач2, ...);
Некоторые возможные сочетания свойств и их значений приведены в следующей
таблице:
15

16.

Вычисление определенных интегралов
Первым шагом является создание функции, вычисляющей подынтегральное
выражение, ее текст:
function f = fint(x)
f = exp(-x).*sin(x);
Теперь для вычисления интеграла вызовите quad, задав первым аргументом
ссылку на функцию fint, а вторым и третьим – нижний и верхний пределы
интегрирования. В качестве выходного аргумента можно указать имя переменной, в
которую следует записать найденное значение:
>> format long
>> I = quad(@fint,-1,1)
I=
-0.66349146785310
По умолчанию функция quad вычисляет приближенное значение интеграла с
точностью 10-6. Для изменения точности вычислений следует задать
дополнительный четвертый аргумент:
>> I = quad(@fint,-1,1,1.0e-07)
I=
-0.66349366574399
16

17.

Вычисление двойных интегралов
В MATLAB определена функция dblquad для приближенного вычисления
двойных интегралов. Как и в случае вычисления определенных интегралов, следует
написать файл-функцию для вычисления подынтегрального выражения.
Функция fint2 должна содержать два входных аргумента х и у, ее текст:
function f = fint2(x, y)
f = exp(x).*sin(y) + exp(-x).*cos(y);
Функция dblquad имеет пять входных аргументов, при ее вызове необходимо
учесть, что первыми задаются пределы внутреннего интеграла по х, а вторыми –
внешнего по у:
>> dblquad(@fint2, -pi, pi, 0, 1)
ans =
30.0537
Дополнительным шестым параметром можно задать точность вычисления
интеграла.
>> format long
>> dblquad(@fint2, -pi, pi, 0, 1, 1.0e-012)
ans =
30.05371586580528
17

18.

18

19.

Символьные переменные и функции
Создание символьных переменных.
Допустим, что требуется выполнить сложение (символьное, а не
численное) алгебраического выражения x+y и выражения 3y.
Получить такой результат средствами ядра пакета MATLAB
нельзя, так как там осуществляются только численные расчеты, а в
сформулированной задаче вообще не заданы никакие численные значения для
переменных x и y, входящих в исходное выражение.
Вот здесь на помощь и приходит Symbolic Math Toolbox.
x=sym('x'); y=sym('y');
x+y+3*y
ans =
x+4*y
Этот пакет осуществляет сложение над объектами нового типа –
sym-объекты. Такие объекты получаются после вызова одноименной
функции конструктора таких объектов. Над объектами типа sym
производятся манипуляции в соответствии с правилами алгебры и
математического анализа.
19

20.

Символьные переменные и функции
Другой способ создания переменных типа sym, который позволяет
достаточно компактно инициализировать большое количество переменных,
это использование функции syms. Например, инициализацию переменных x и y
из прошлого примера, можно записать в виде:
syms x, y
Можно создавать переменные типа sym, сразу инициализируя их
алгебраические выражения, например:
Expr1 = sym('x+4*y');
20

21.

Символьные переменные и функции
Упрощение, преобразование и вычисление выражений.
Функция simplify (упрощать) осуществляет поэлементное упрощение символьных
выражений. Если упрощение невозможно, возвращается исходное выражение.
Например:
>> simplify((x^2-2*x*y+y^2)/(x-y))
ans =
x-y
Дополнительные возможности обеспечивает функция simple(s). При
обращении к функции simple в форме
[R,HOW]=simple(s) промежуточные
результаты не выводятся. Конечные результаты упрощений содержатся в векторе
R, а в строковом векторе HOW указывается выполняемое преобразование.
syms x
[R1,HOW1]=simple(cos(x)^2-sin(x)^2)
[R2,HOW2]=simple(2*cos(x)^2-sin(x)^2)
возвращает следующие результаты:
R1 =
cos(2*x)
HOW1 =
combine
R2 =
3*cos(x)^2-1
HOW2 =
simplify
21

22.

Символьные переменные и функции
Функция expand (раскрывать)
функциональные выражения.
>> expand(sin(x+y))
ans =
sin(x)*cos(y)+cos(x)*sin(y)
призвана
раскрывать
алгебраические
и
Ясно, что так можно запрашивать подсказки по забытым формулам алгебры и
тригонометрии. Можно просто перемножать многочлены.
>> expand((x+y)*(x-y)*(2*x-3*y))
ans =
2*x^3-3*x^2*y-2*y^2*x+3*y^3
Функция pretty(Expr).
С помощью функции factor (множитель, сомножитель) можно раскладывать
многочлены на простые множители:
>> factor(x^4+2*x^3-3*x^2)
ans =
(x-1)*(x+3)*x^2
22

23.

Пределы, дифференцирование и интегрирование
Функция limit находит предел функции в некоторой точке, включая и плюс
или минус бесконечность. Первым входным аргументом limit является символьное
выражение, вторым – переменная, а третьим – точка, в которой разыскивается
предел.
limit(f,a) – возвращает предел в точке a символьного выражения f по
независимой переменной.
limit(f) – возвращает предел в точке a=0 символьного выражения f по
независимой переменной.
limit(f,x,a) – возвращает предел символьного выражения f в точке x=a.
limit(f,x,a,'right') – возвращает предел символьного выражения f в точке
x=a+0 (справа).
limit(f,x,a,'left') – возвращает предел символьного выражения f в точке x=a-0
(слева).
Для получения ответа определите a и x, как символьные
переменные, и используйте inf в качестве точки предела:
syms a x
limit((1 + 1/x)^(x*a), x, Inf)
ans =
exp(a)
23

24.

Пределы, дифференцирование и интегрирование
Операции символьного дифференцирования и символьного интегрирования.
Первая из них выполняется функцией diff.
diff(s) – возвращает символьное значение первой производной от
символьного выражения или массива символьных выражений s по независимой
переменной.
diff(s,n) – возвращает символьное значение n-й производной от символьного
выражения или массива символьных выражений s по независимой переменной
diff(s,'v') или diff(s,sym('v')) – возвращает символьное значение первой
производной от символьного выражения или массива символьных выражений s по
переменной v.
diff(s,'v',n) или diff(s,n,'v') – возвращает символьное значение n-й
производной от символьного выражения или массива символьных выражений s по
переменной v.
Вот соответствующие примеры:
>> y=x^2-4*x-7;
>> diff(y,x)
ans =
2*x-4
Здесь выражение diff(y,x) означает «продифференцировать» y по x. Чтобы найти
производную порядка n необходимо его указать дополнительным параметром:
>> syms x t
>> y2=diff(2*x+x*t^6,t,5)
y2 =
24
720*x*t

25.

Пределы, дифференцирование и интегрирование
Для вычисления определенных и неопределенных интегралов в символьном
виде служит функция int.
int(s) – возвращает символьное значение неопределенного интеграла от
символьного выражения или массива символьных выражений s по переменной. Если s –
константа, то вычисляется интеграл по переменной 'x'.
int(s,a,b) – возвращает символьное значение определенного интеграла на
отрезке интегрирования [a,b] от символьного выражения или массива символьных
выражений s по переменной. Пределы интегрирования a, b могут быть как
символьными, так и числовыми.
int(s,v) – возвращает символьное значение неопределенного интеграла от
символьного выражения или массива символьных выражений s по переменной v.
int(s,v,a,b) – возвращает символьное значение определенного интеграла от
символьного выражения или массива символьных выражений s по переменной v с
пределами интегрирования [a,b].
25

26.

Пределы, дифференцирование и интегрирование
А теперь пример на интегрирование:
y=1/sin(x);
int(y,x)
ans =
log(csc(x)-cot(x))
Примеры интегрирования по разным переменным:
>> syms x t y1 y2
И пример на вычисление определенного
>> y1=int(t*sin(x),x)
интеграла:
y1 =
>> syms x y a b
-t*cos(x)
>> y=cos(x);
>> y2=int(t*sin(x),t)
>> int(y, x, a, b)
y2 =
ans =
1/2*t^2*sin(x)
sin(b)-sin(a)
>> int(y, x, -pi/2, pi/2)
ans =
2
В первом случае пределы интегрирования являются символьными, а во втором
числовыми.
26

27.

Вычисление сумм рядов
где i – переменная суммирования, служит функция symsum. Параметр b может быть
конечным или бесконечном (inf).
symsum(s) – возвращает символьное значение суммы бесконечного ряда по
переменной суммирования, найденной автоматически.
symsum(s,a,b) – возвращает символьное значение суммы ряда по переменной
суммирования, найденной автоматически, при изменении этой переменной от а до b.
symsum(s,v) – возвращает символьное значение суммы бесконечного ряда по
переменной суммирования v.
symsum(s,v,a,b) – возвращает символьное значение суммы бесконечного ряда
по переменной суммирования v при изменении этой переменной от а до b.
Пример:
>> syms k n
>> y1=simple(symsum(k))
>> y2=simple(symsum(k,0,n-1))
>> y3=simple(symsum(k,0,n))
>> y4=simple(symsum(k^2,0,n))
возвращает следующие результаты:
y1 =
1/2*k*(k-1)
y2 =
1/2*n*(n-1)
y3 =
1/2*n*(n+1)
y4 =
1/6*n*(n+1)*(2*n+1)
27

28.

Разложение в ряд Тейлора
При a =0 этот ряд называется рядом Маклорена. Для получения разложений
аналитических функций в ряд Тейлора служит функция taylor.
taylor(f) – возвращает 6 членов ряда Маклорена.
taylor(f,n) – возвращает члены ряда Маклорена до (n-1)-го порядка.
taylor(f,a) – возвращает 6 членов ряда Тейлора в окрестности точки a.
taylor(f,a,n) – возвращает члены ряда Тейлора до (n-1)-го порядка в окрестности
точки a.
Пример использования:
y=sin(x);
taylor(y,0,6)
ans =
x-1/6*x^3+1/120*x^5
28

29.

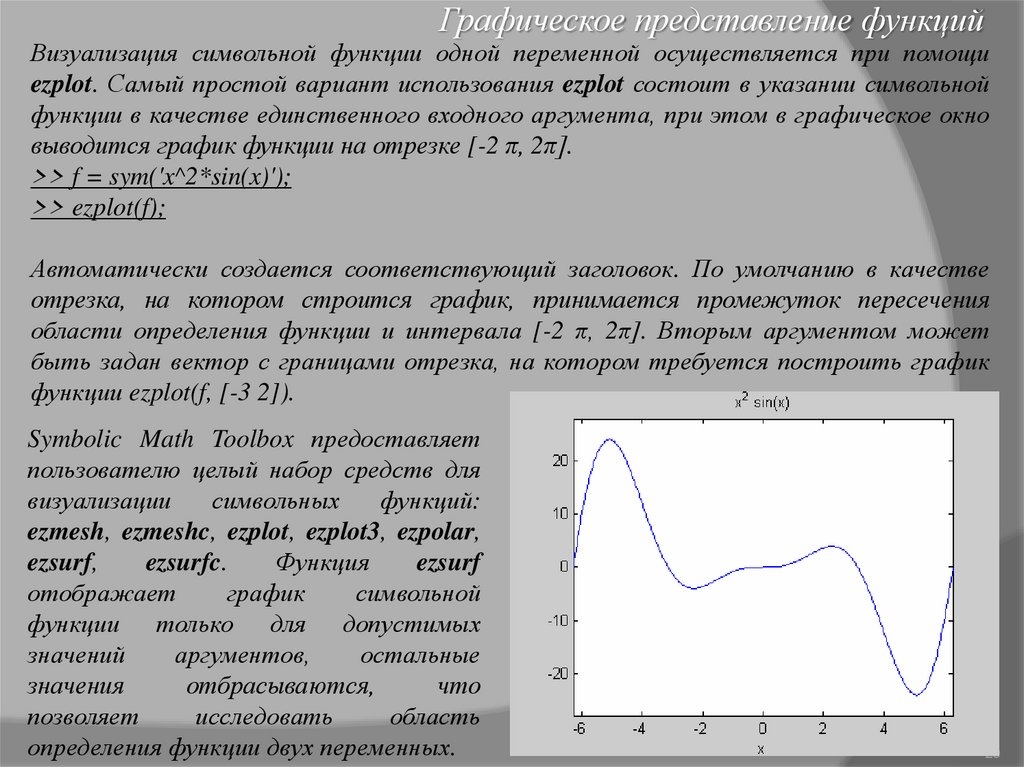
Графическое представление функций
Визуализация символьной функции одной переменной осуществляется при помощи
ezplot. Самый простой вариант использования ezplot состоит в указании символьной
функции в качестве единственного входного аргумента, при этом в графическое окно
выводится график функции на отрезке [-2 π, 2π].
>> f = sym('x^2*sin(x)');
>> ezplot(f);
Автоматически создается соответствующий заголовок. По умолчанию в качестве
отрезка, на котором строится график, принимается промежуток пересечения
области определения функции и интервала [-2 π, 2π]. Вторым аргументом может
быть задан вектор с границами отрезка, на котором требуется построить график
функции ezplot(f, [-3 2]).
Symbolic Math Toolbox предоставляет
пользователю целый набор средств для
визуализации
символьных
функций:
ezmesh, ezmeshc, ezplot, ezplot3, ezpolar,
ezsurf,
ezsurfc.
Функция
ezsurf
отображает
график
символьной
функции только для допустимых
значений
аргументов,
остальные
значения
отбрасываются,
что
позволяет
исследовать
область
определения функции двух переменных.
29