Похожие презентации:
Комбинаторика
1. Комбинаторика
Лектор: Завьялов Олег Геннадьевичкандидат физико-математических наук, доцент
2. Комбинаторика.
Комбинаторика – это раздел математики, в котором изучаютсявопросы выбора или расположения элементов множества в
соответствии с заданными правилами.
Важно! Комбинаторика рассматривает конечные множества.
3.
Перестановки и их число.Определение.
Перестановкой называется множество из n элементов,
записанных в определённом порядке.
Теорема о перестановках элементов конечного множества:
n различных элементов можно расставить по одному на n
различных мест ровно n! способами.
Число перестановок из n различных элементов
обозначается Pn.
Рn n!
4.
РазмещенияОпределение 1. Пусть дано n-элементное множество. Любая
упорядоченная k-элементная выборка из этого множества
называется размещением из n элементов по k.
Число k-размещений без повторений n-элементного множества
обозначается
(или A(n,m)). Без повторений – это значит, что все k
элементов должны быть различными.
Число k-размещений с повторением n-элементного множества
обозначается
. С повторением – значит, что среди выбранных k
элементов могут встречаться одни и те же.
5.
РазмещенияПример. Выпишем все 2-размещения 3-элементного множества
A={a,b,c}.
Без повторений: {a;b},{b,a},{a;c},{c,a},{b,c},{c;b}.
С повторением: {a;b},{b,a},{a;c},{c,a},{b,c},{c;b},{a;a},{b;b},{c;c}.
Таким образом,
= 6,
= 9.
6.
РазмещенияВычислим
Если элементы в размещении не могут повторяться, то число способов
выбора каждого очередного элемента размещения будет на единицу
меньше, чем для предшествующего ему. А так как первый элемент
выбирается n способами, то получаем формул
Вычислим
В размещении с повторениями каждый очередной элемент может быть
выбран n способами, поэтому
7.
Сочетания. Свойства сочетаний. Бином НьютонаОпределение 1. Пусть дано n-элементное множество. Любое kэлементное подмножества множества A называется k-сочетанием nэлементного множества.
Число k-сочетаний n-элементного множества обозначается
C(n,m)).
Пример. Выпишем все 2-сочетания 4-элементного множества
A={a,b,c,d}: {a;b},{a;c},{a;d},{b,c},{b,d},{c,d}.
Таким образом,
(или
8.
Сочетания. Свойства сочетаний. Бином НьютонаТеорема 2.
при k n.
Доказательство. Из одного k-сочетания можно получить k! различных
k-размещений n-элементного множества, потому что k элементов
можно упорядочить k! способами. Поскольку каждое k-размещение
есть не что иное, как упорядоченное k-сочетание, то всего kразмещений будет
.
С другой стороны k-размещений имеется
Получили равенство
или
,
и отсюда получаем искомую формулу:
.
. Ч.т.д.
9.
Пример. Пять девушек и трое юношей играют в волейбол. Сколькимиспособами они могут разбиться на две команды по четыре человека,
если в каждой команде должно быть хотя бы по одному юноше.
Решение. Понятно, если мы отберём одну команду из четырёх
человек, то вторая определится автоматически. Сколькими способами
можно выбрать четыре человека из восьми, чтобы в ней были один или
два юноши. Посчитаем команды 1-го типа (содержащие одного юношу).
Одного юношу из трёх можно выбрать
способами, трёх девушек
из 5 можно выбрать
способами.
По принципу произведения число команд 1 типа равно
Аналогично, команд второго типа (содержащих двух юношей)
существует
Но при таком подсчёте каждое разбиение на команды учитывалось
дважды. Поэтому окончательный ответ: трёх юношей и четырёх
девушек можно разбить на две команды, удовлетворяющие
условию задачи, 30-ю способами.
10.
Теорема. Простейшие свойства сочетаний.1)
2)
3)
4)
5)
(m 1).
11.
Теорема. Простейшие свойства сочетаний.Доказательство.
1)
2)
12.
Теорема. Простейшие свойства сочетаний.Доказательство. (продолжение)
3)
4)
13.
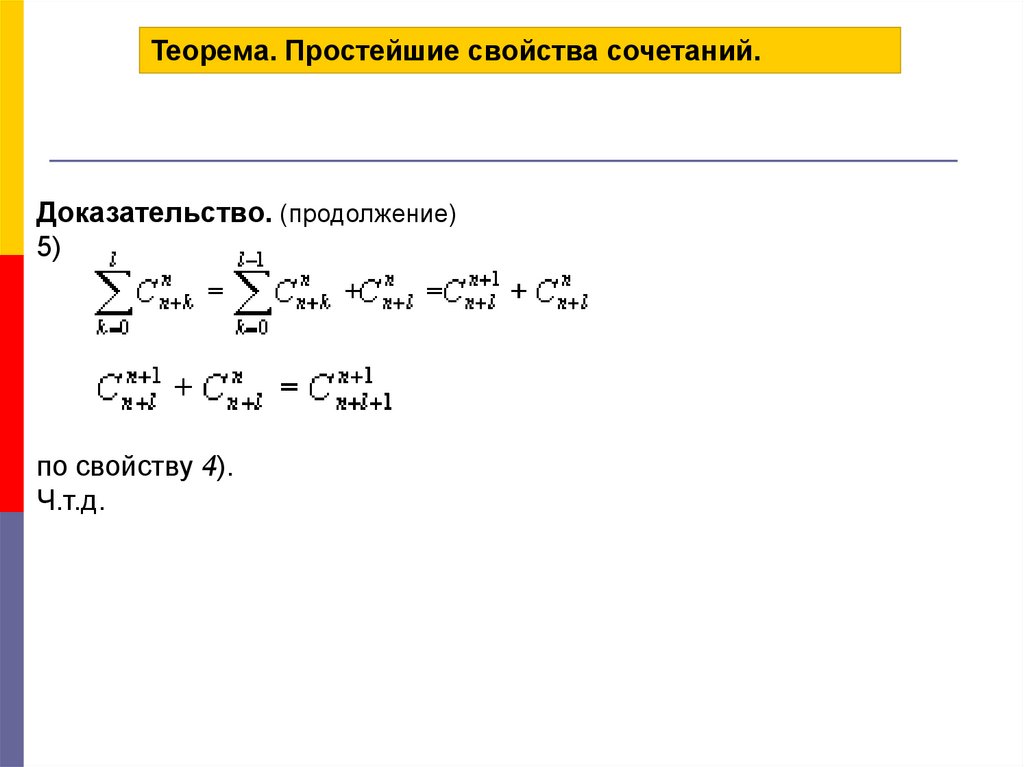
Теорема. Простейшие свойства сочетаний.Доказательство. (продолжение)
5) Это равенство доказывается индукцией по m. При m=1 левая часть
равна
правая часть равна
приm=1 доказываемое равенство выполняется.
Допустим равенство выполняется при m=l
Докажем равенство при m=l+1, то есть докажем равенство
14.
Теорема. Простейшие свойства сочетаний.Доказательство. (продолжение)
5)
по свойству 4).
Ч.т.д.
15.
Теорема. (бином Ньютона).Доказательство. Второе равенство представляет собой не что иное, как
разные записи одной и той же суммы. Слева стоит эта сумма в “развернутом”
виде, а справа эта же сумма, записанная с помощью знака суммирования.
Поэтому доказываем первое равенство.
Рассмотрим выражение:
В первой сумме количество слагаемых равно количеству элементов
множества S={1, 2, …, n}, то есть
.
Во второй сумме количество слагаемых равно количеству двухэлементных
подмножеств n-элементного множества S, то есть равно
16.
Теорема. (бином Ньютона).Доказательство. (продолжение)
Число слагаемых в k-ой сумме равно количеству k-элементных подмножеств nэлементного множества S , то есть равно
.
Поэтому, если положить в А
Ч.т.д.
17.
Следствие.Доказательство.
Положим в формуле бинома х=1, получим доказываемое равенство.
Равенство из следствия имеет очень важный комбинаторный смысл. В
правой части:
- количество пустых подмножеств n-элементного множества S,
- количество 1-элементных подмножеств n-элементного множества S
- число k – элементных подмножествn-элементного множества и так
далее. Сумма в правой части представляет собой количество всех
подмножеств n–элементного множества, а записанное равенство показывает,
что таких подмножеств будет 2n.
Таким образом, следствие можно сформулировать так: если n(S) = n, то n(P(S))
= 2n, где S - n-элементное множество, P(S) – булеан множества S.
18.
Следствие.Доказательство.
Положим в формуле бинома x = -1, тогда получим доказываемое равенство.
Следствие.
(a+b)n =
Доказательство.
Положим в формуле бинома x = b/a. Получим
(1 + b/a)n =
(1 + b/a)n =
. Домножим это равенство на an:
(a+ b)n =
Часто именно эту формулу называют биномом Ньютона.
19.
Следствие.Замечание.
В силу большой важности бинома Ньютона для самых разных разделов
математики, числа
называются биноминальным коэффициентами.
20.
Задача. Треугольник ПаскаляПостоим бесконечную таблицу натуральных чисел следующим
образом. В первой строке все числа равны 0, кроме одного, которое равно 1.
Числа второй строки записывают строго между числами первой строки и равны
они сумме двух чисел первой строки, между которыми они стоят. Допустим,
построена k-я строка. Тогда числа (k+1) – ой строки записываются между
числами k-ой строки и равны сумме двух чисел k-ой строки, между которыми
они стоят: элемент, стоящий в k-й строке на i-м месте равен
21.
Определение.Пусть А = {a1, a2, …, an} - n–элементное множество.
k-сочетанием с повторениями множества А называется неупорядоченный
набор [ai1, a i2, …, ain], где все элементы принадлежат множеству А, причем
допустимо повторение этих элементов.
Пример. Пусть А = {a, b, c}. Все 2-сочетания с повторениями множества А:
[a, a], [a, b], [a, c], [b, b], [b, c], [c,c].
Число k–сочетаний с повторениями n-элементного множества обозначается .
Пример показывает, что .
22.
ЛеммаЧисло всех упорядоченных последовательностей из нулей и единиц длины n, в
которых присутствует l нулей, равно
(или
, что одно и то же).
Доказательство. Пусть в некоторой последовательности нули стоят на
местах k1,k2,…,kl (ki ≤ n). Очевидно, множество {k1,k2,…,kl}
{1,2,…,n} однозначно определяет эту последовательность. Обратно, каждому
подмножеству {k1,k2,…,kl} множества {1,2,…,n} сопоставляем
последовательность, на местах с этими номерами в которой ставим нули, на
остальных местах – единицы. Значит, искомых последовательностей
существует столько же, сколько l-элементных подмножеств n-элементного
множества, то есть
.
23.
Теорема.Доказательство.
Будем строить k-элементные сочетания с повторением из элементов nэлементного множества А={а1, а2, …, аn}. В каждом таком наборе сначала
расположим элементы типа а1, потом типа а2 и так далее. Каждому kсочетанию с повторениями поставим в соответствие последовательность из
нулей и единиц длины n+k=1. Число единиц в этой последовательности
равно k, а число нулей равно n-1. Каждый 0 отделяет набор типа аi от
набора аi+1 в данном k-сочетании с повторениями. В частности, если 0 стоит
на первом месте, то это означает, что элементов типа а1, в данном k-сочетаний
нет; если нет элементов типа аi, то между единицами, соответствующими
элементам типа аi-1 и аi+1 стоит два нуля. (проиллюстрируем эту конструкцию:
пусть А= {а1, а2, а3, а4};
6-сочетанию [а1, а1, а2, а3, а3, а4] соответствует последовательность
(1, 1, 0, 1, 0, 1, 1, 0, 1).
Каждое k-сочетание с повторением однозначно определяет указанную
последовательность и наоборот. По лемме 11 таких последовательностей
существует
24.
Пример.Задача. В магазине продаются пирожные 4 сортов. Сколькими способами
можно купить 8 пирожных?
Решение. Находим число 8-сочетаний с повторениями 4-х элементного
множества:
(способов).
25.
ВыборкаБез
повторений
С
повторениями
Упорядоченная
n!
Anm
(n m)!
m
n
А n
m
Неупорядоченная
n!
m
Cn
m! ( n m )!
C
m
n
( n m 1)!
m! ( n 1)!
26.
Последний слайд лекции!!
























 Математика
Математика








