Двоично-десятичная система счисления

1.

Двоично – десятичная система
счисления
Двоично-десятичная система счисления широко
используется в цифровых устройствах, когда основная
часть операций связана не с обработкой и хранением
вводимой информации, а с ее вводом и выводом на
какие-либо индикаторы с десятичным представлением
полученных результатов (микрокалькуляторы,
кассовые аппараты и т. п.).

2.

Двоично-десятичные коды
Двоично-десятичный код — форма записи
чисел, когда каждый десятичный разряд
числа записывается в виде его
четырёхбитного двоичного кода (0…9).
Пример:
Записать число
584610 в двоично-десятичном коде.
0101
1000
0100
0110
5
8
4
6
Ответ : 0101100001000110

3.

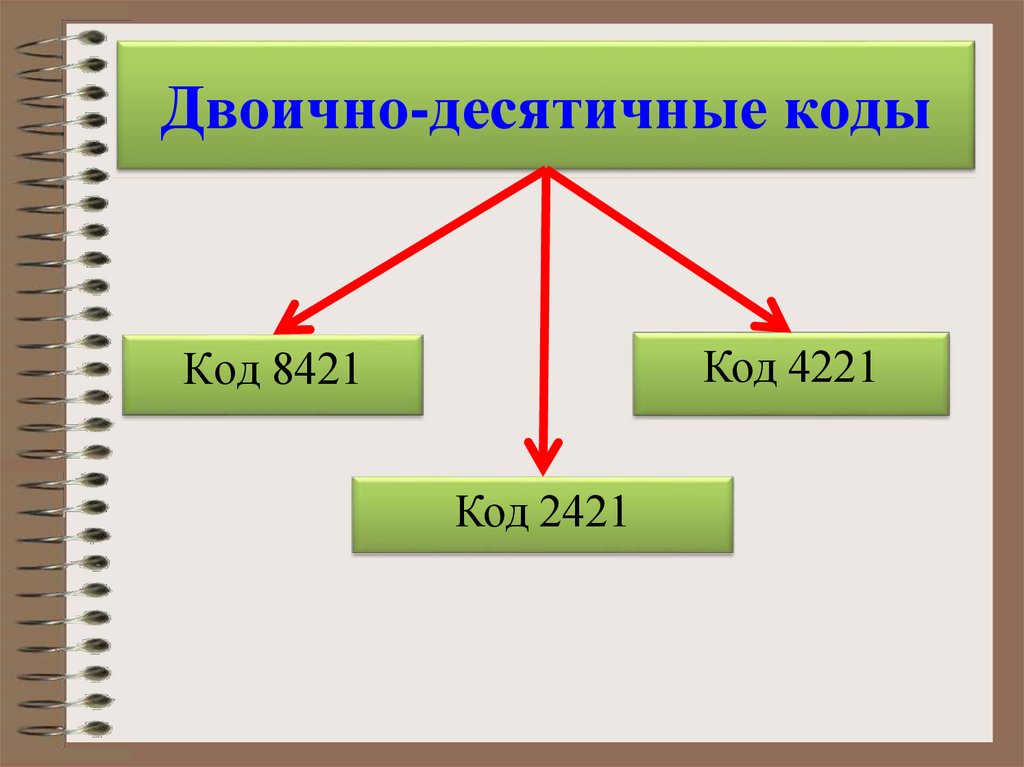
Двоично-десятичные коды
Код 4221
Код 8421
Код 2421

4.

Код 8421
Обычный перевод каждой цифры
десятичного числа в четырёхбитный
(четырёхзначный) двоичный код.
Пример:
Записать число
584610 в двоично-десятичном коде 8421 .
0101
1000
0100
0110
5
8
4
6
Ответ : 0101100001000110

5.

Таблица 8421
Десятичный код
Двоично-десятичный 8421
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001

6.

Код 2421
Двоичный код 010 − 410 похож на код
8421,
двоичный код 510 − 910 содержат избыток
«+6»
Пример:
Записать число
584610 в двоично-десятичном коде 2421 .
1011
1110
0100
1100
5
8
4
6
Ответ : 1011111001001100

7.

Таблица 2421
Десятичный код
Двоичнодесятичный 8421
Двоично-десятичный 2421
С 0-4 похож на 8421, с 5-9
прибавляем «+6»
0
0000
0000
1
0001
0001
2
0010
0010
3
0011
0011
4
0100
0100
5
0101
0101+0110=1011
6
0110
0110+0110=1100
7
0111
0111+0110=1101
8
1000
1000+0110=1110
9
1001
1001+0110=1111

8.

Код 4221
Чтобы получить код 4221 числа 0-9, надо
к двоичному коду 8421 прибавить «+3».
Пример:
Записать число
584610 в двоично-десятичном коде 4221 .
1000
1011
0111
1001
5
8
4
6
Ответ : 1000101101111001

9.

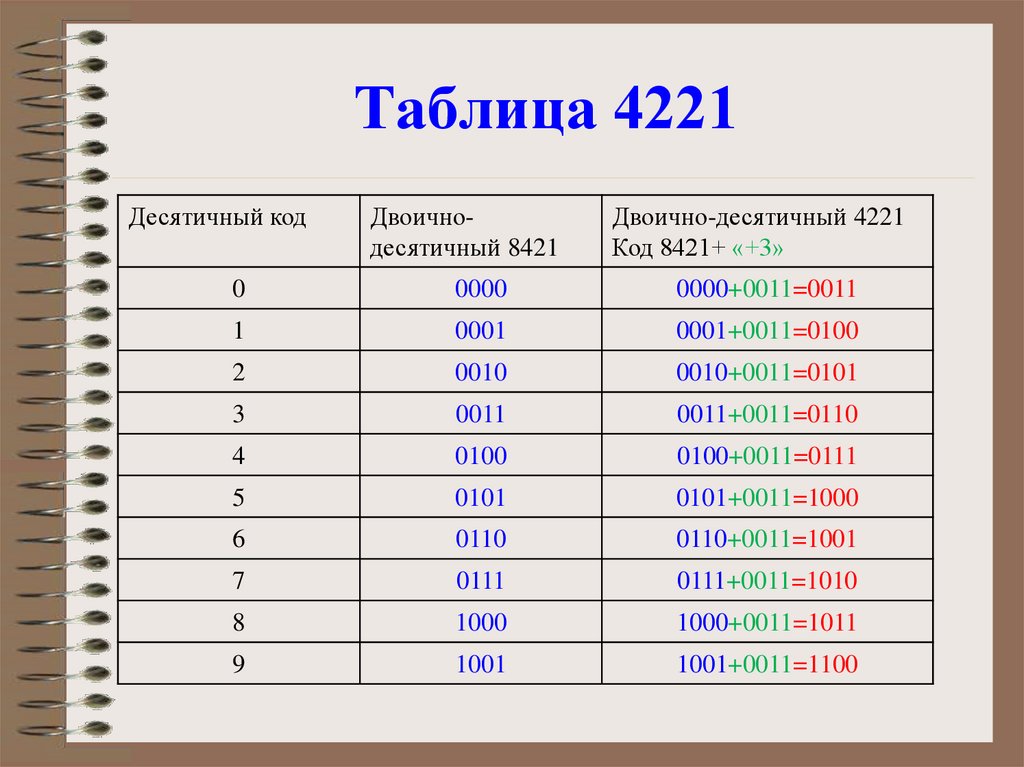
Таблица 4221
Десятичный код
Двоичнодесятичный 8421
Двоично-десятичный 4221
Код 8421+ «+3»
0
0000
0000+0011=0011
1
0001
0001+0011=0100
2
0010
0010+0011=0101
3
0011
0011+0011=0110
4
0100
0100+0011=0111
5
0101
0101+0011=1000
6
0110
0110+0011=1001
7
0111
0111+0011=1010
8
1000
1000+0011=1011
9
1001
1001+0011=1100

10.

Сложение и вычитание
Сначала производится подготовительная операция, называемая выравниванием порядков.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем
регистре вправо на количество разрядов, равное разности порядков операндов.
После каждого сдвига порядок увеличивается на единицу, а освободившиеся старшие
разряды заполняются нулями. В результате выравнивания порядков одноименные разряды
чисел оказываются расположенными в соответствующих разрядах обоих регистров, после
чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы
результата влево.
Нормализацией называется выбор такого значения порядка, при котором старший разряд
мантиссы имеет значение 1. При нормализации возможны две ситуации:
− результат меньше 1/2, то есть старшие разряды мантиссы нулевые. Если при этом
результат представлен в прямом коде, мантисса сдвигается влево до тех пор, пока первая
значащая 1 не окажется в старшем разряде. Если же результат представлен в обратном или
дополнительном коде (отрицательный), производится сдвиг влево до появления в старшем
разряде первого значащего нуля. При каждом сдвиге значение порядка уменьшается на 1;
− результат больше 1, то есть разрядная сетка переполнена. В этом случае мантисса
сдвигается вправо на один разряд с одновременным увеличением порядка на 1.
Правила выполнения основных арифметических операций справедливы для чисел любой
позиционной системы счисления.

11.

Примеры
1) Сложить десятичные нормализованные числа 0,536·106и 0,284·103.
Разность порядков слагаемых здесь равна трём (6-3=3), поэтому перед сложением мантисса второго числа
сдвигается на три разряда вправо
2) Сложить двоичные нормализованные числа 0,11011·210 и 0,10111·2–1.
Разность порядков слагаемых здесь равна трем (102+12=112=310), поэтому перед сложением мантисса
второго числа сдвигается на три разряда вправо
3) Сложить шестнадцатеричные нормализованные числа 0,1В5·163 и 0,34Е·16–1.
Разность порядков слагаемых здесь равна четырём (316+116=416=410), поэтому перед сложением мантисса
второго числа сдвигается на четыре разряда вправо

12.

Задания
1. Закодируйте число 1234 в двоичнодесятичной системе счисления (все
кодировки).
2. Запишите число 0111100001101001ддс в
десятичной системе счисления.