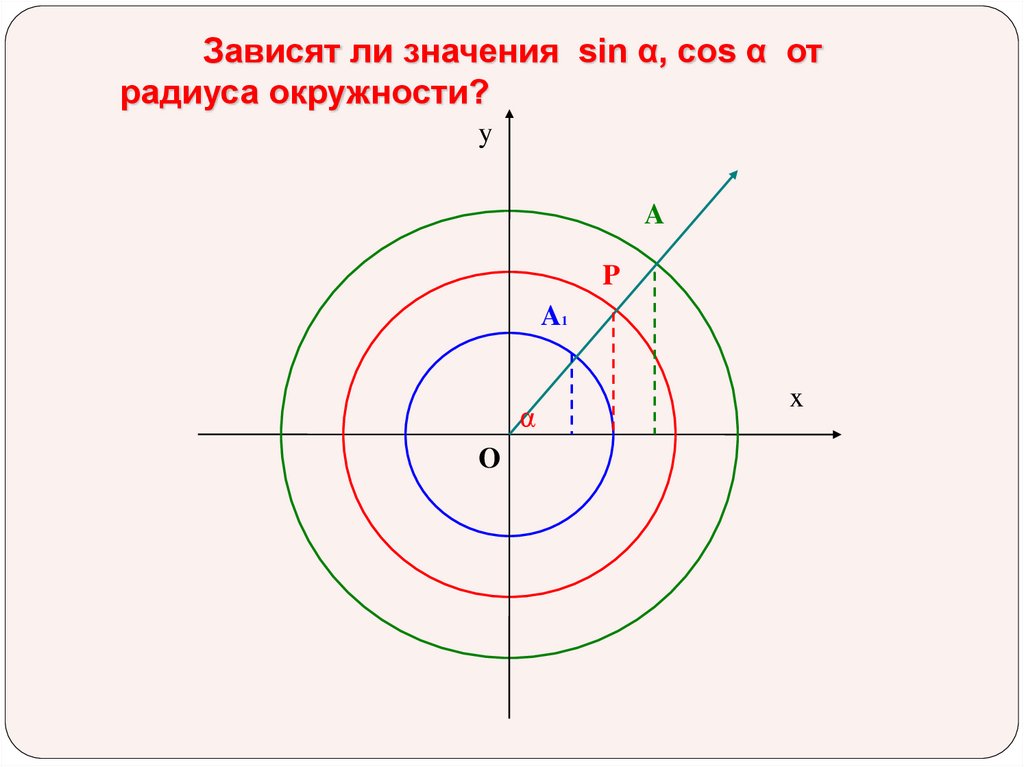
Зависят ли значения sin α, cos α от радиуса окружности?

1. Закончите предложения:

Определите верны или нет следующие утверждения:
1. Существует прямоугольный треугольник с
гипотенузой 8 и катетами 6 и 10
2. В треугольнике любая сторона меньше суммы
двух других сторон.
3. Сумма углов треугольника равна 360
4. В прямоугольном треугольнике синус одного из
углов равен 0.
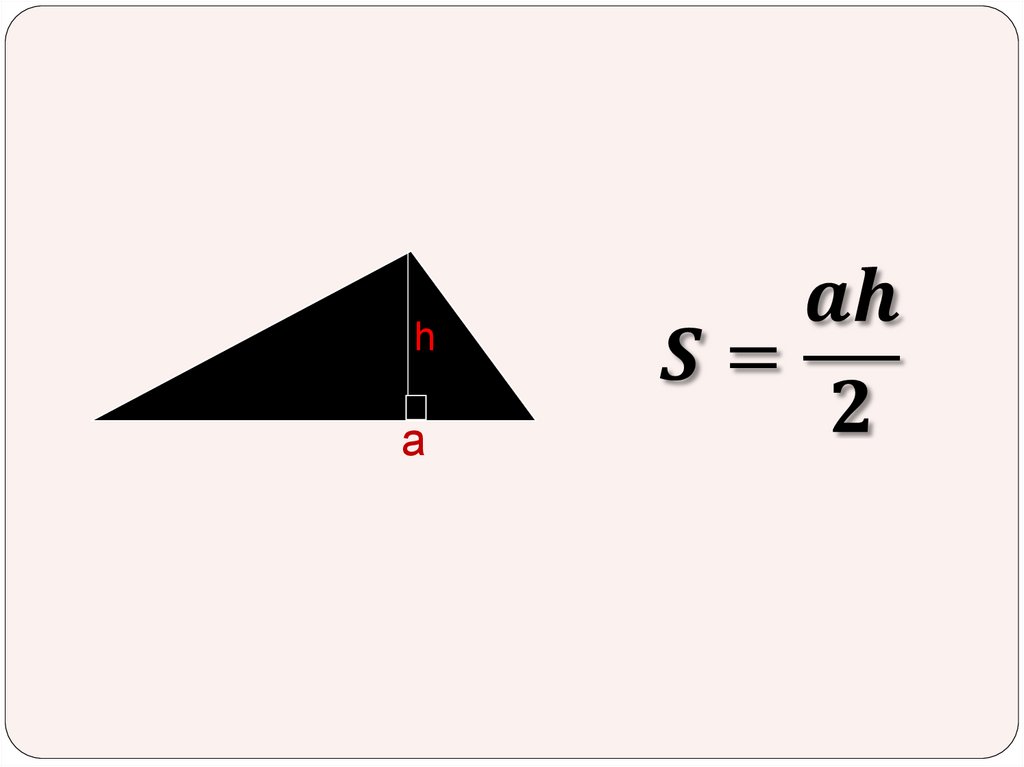
5. Площадь треугольника равна произведению
основания на высоту.
6. Треугольник со сторонами 2,6, 9 существует.
7. Длина гипотенузы прямоугольного треугольника
больше суммы длин его катетов.

2. Определите верны или нет следующие утверждения:

Зависят ли значения sin α, cos α от
радиуса окружности?
y
A
P
A1
α
O
x

3.

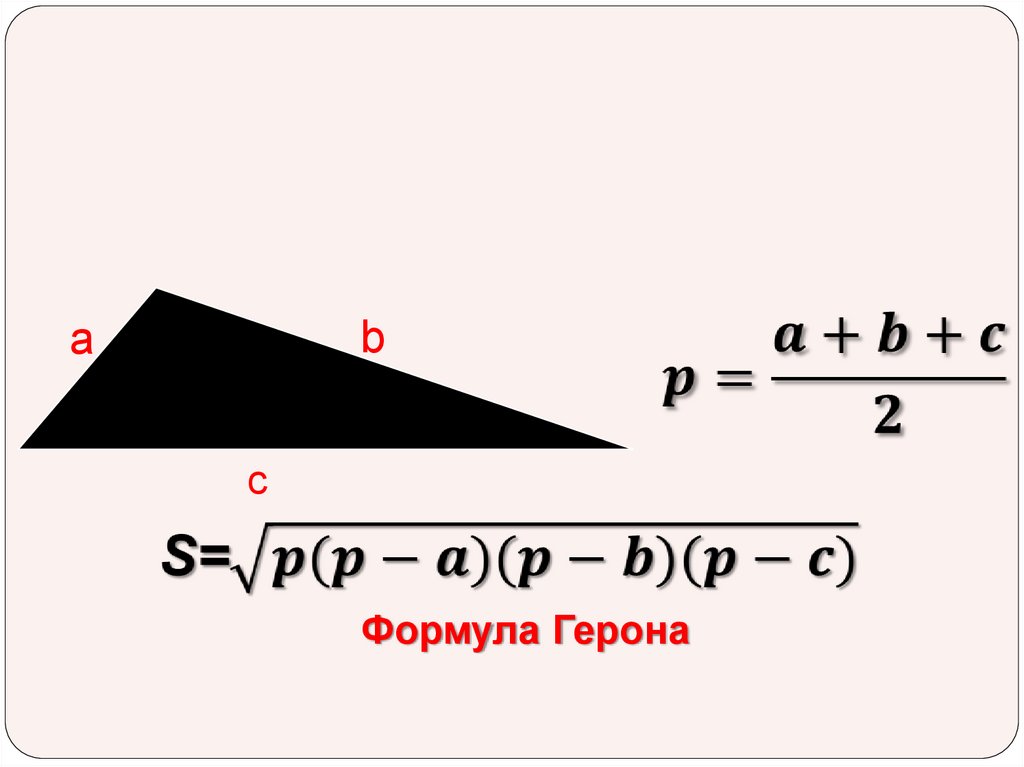
h
a

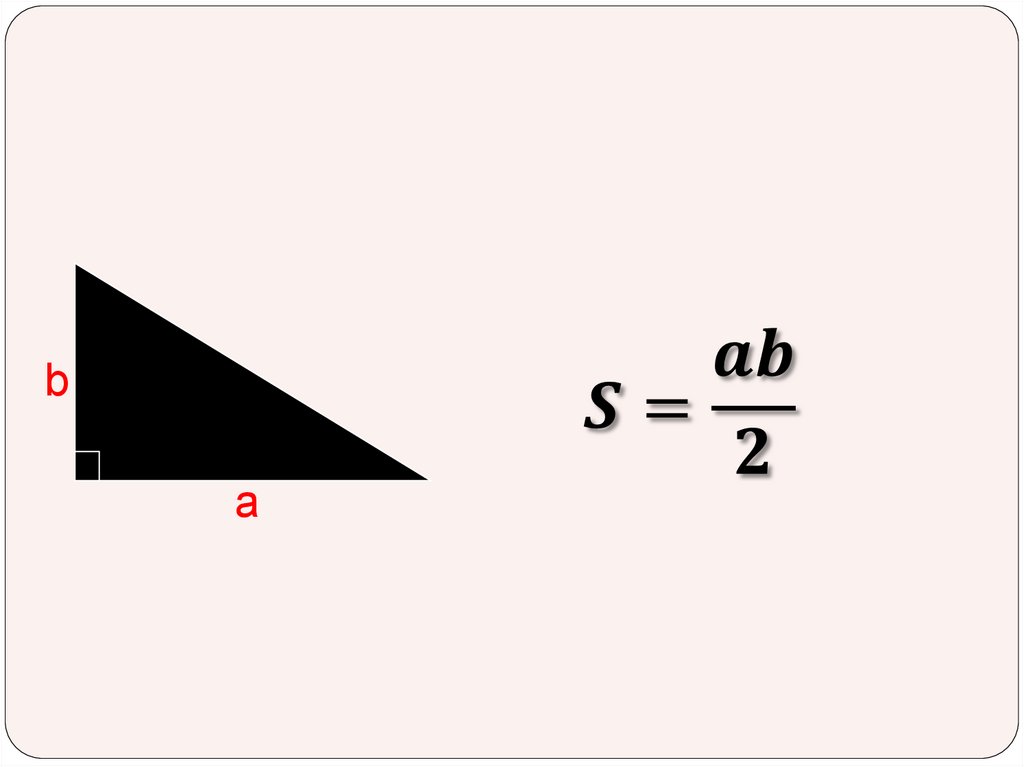
4.

b
a

5.

b
a
c
Формула Герона

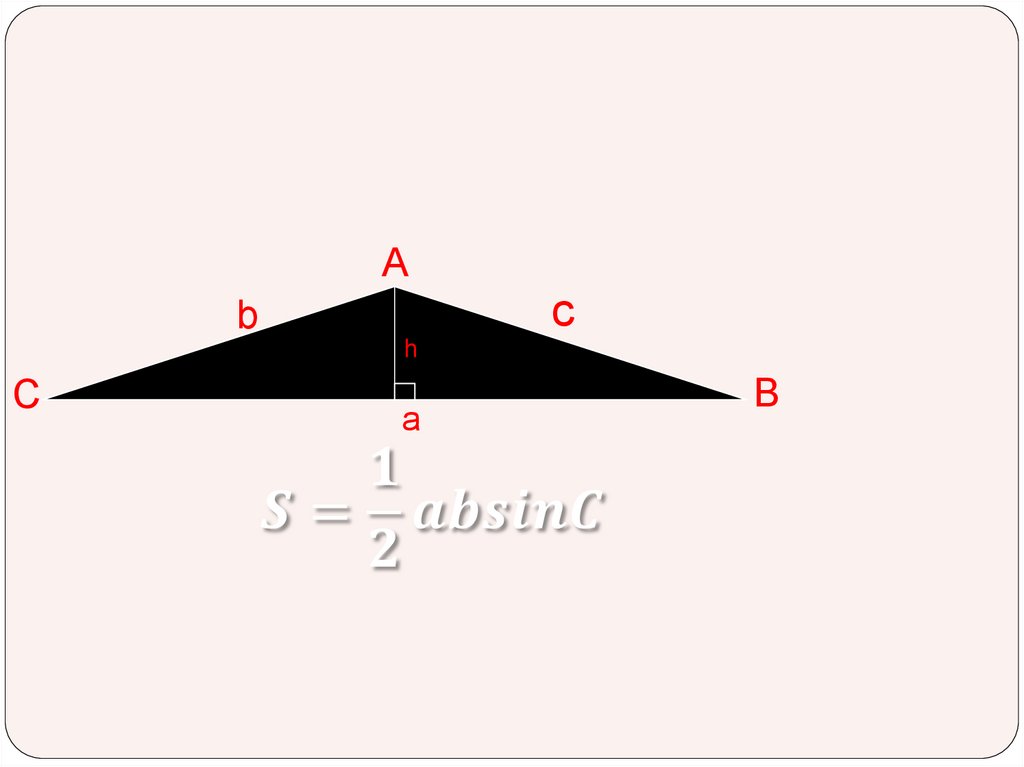
6.

A
c
b
h
C
a
B

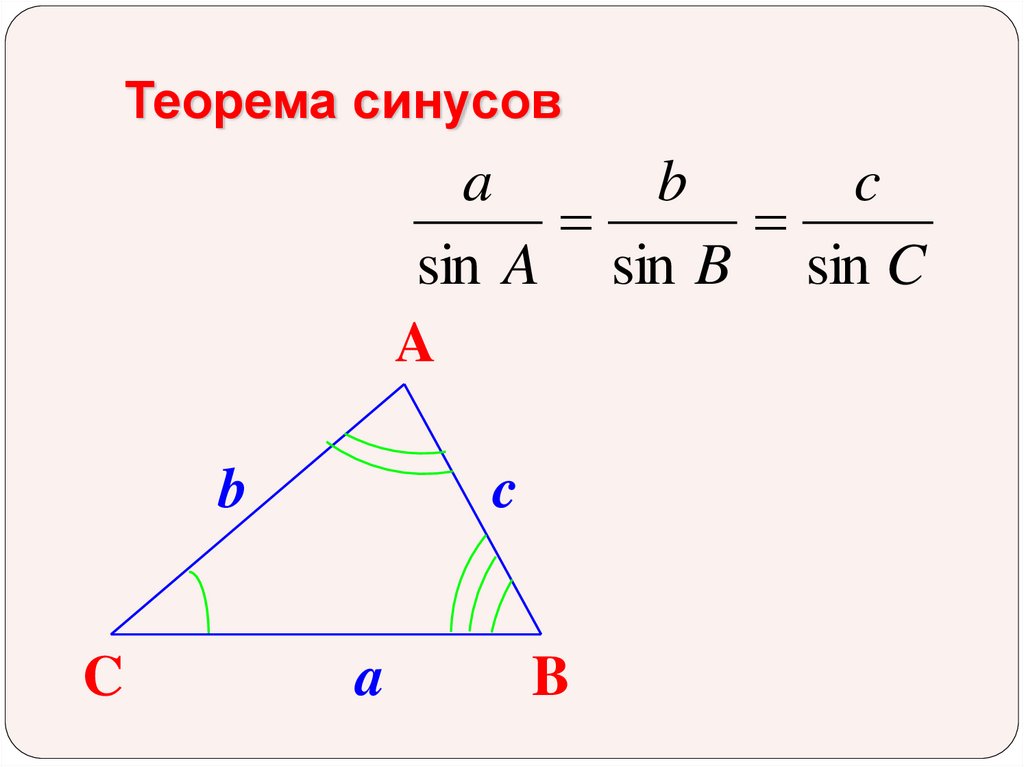
7.

Теорема синусов
a
b
c
sin A sin B sin C
A
b
C
c
a
B

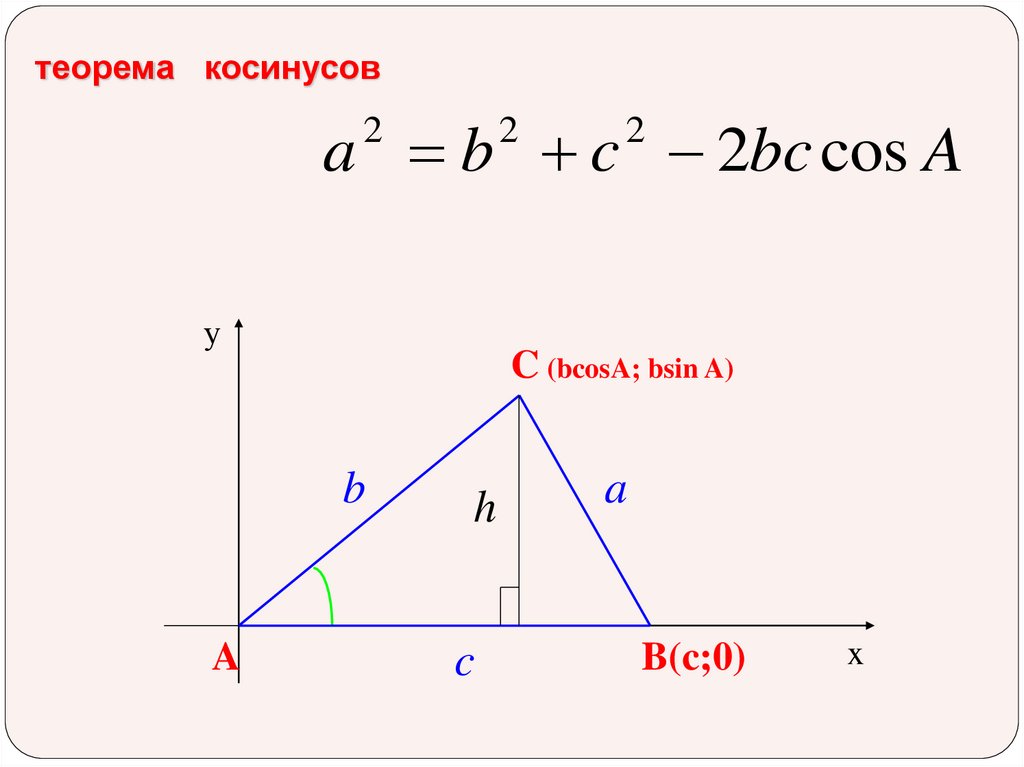
8.

Теорема косинусов

9.

теорема косинусов
a b c 2bc cos A
2
2
у
C (bcosA; bsin A)
b
A
2
h
c
a
B(c;0)
x

10. теорема косинусов

Найдите sinα:
sin 1 cos
2
2
cos ;
5
cos 1;

11.

Найдите cosα, если: sin 1 ;
4
cos 1 sin
2

12.

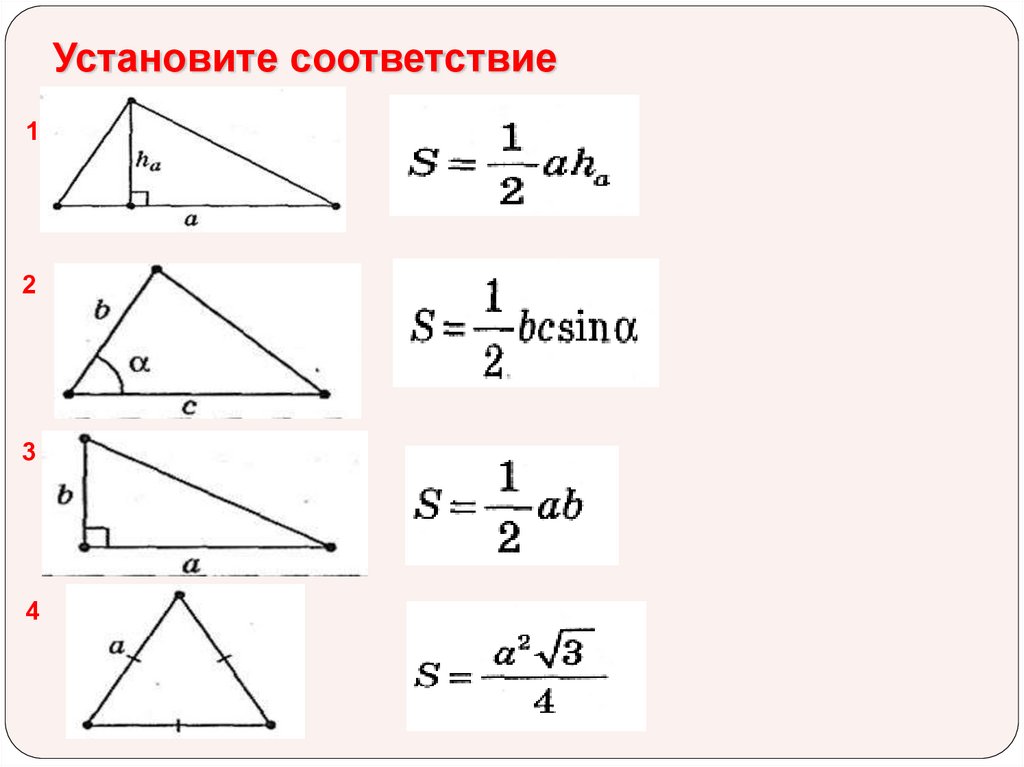
Установите соответствие
1
2
3
4

13.

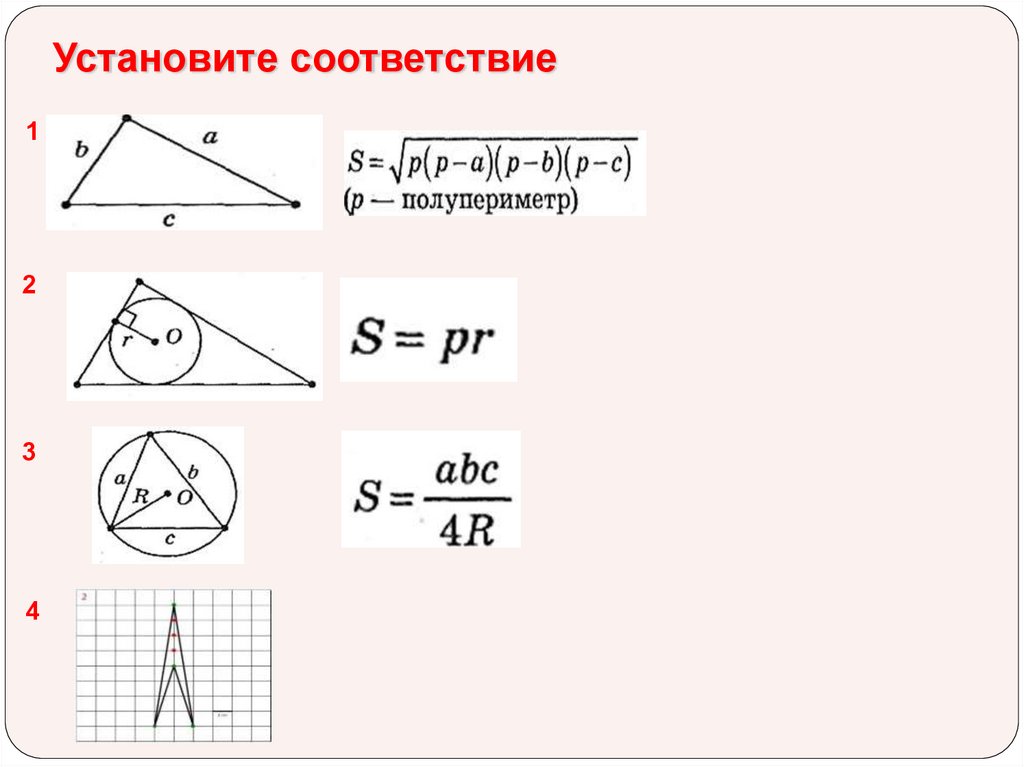
Установите соответствие
1
2
3
4

14.

Формула Пика
Площадь многоугольника
с целочисленными вершинами равна
Г
B+ – 1
2
где
В — количество целочисленных
точек внутри многоугольника, а
Г — количество целочисленных точек на границе
многоугольника.
Формула Пика очень удобна когда сложно догадаться,
как разбить фигуру на удобные многоугольники или
достроить…

15.

Посмотрим, как применить формулу для вычисления площади.
Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В — есть количество целочисленных точек внутри многоугольника,
Г — количество целочисленных точек на границе многоугольника.
В = 10
Г=7
7
10 1 10 3,5 1
2
12,5
В3
1 2 , 5
3
10 х
х

16.

Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В — есть количество целочисленных точек внутри многоугольника,
Г — количество целочисленных точек на границе многоугольника.
В=0
Г=4
4
0 1 2 1
2
В3
1
1
3
10 х
х

17.

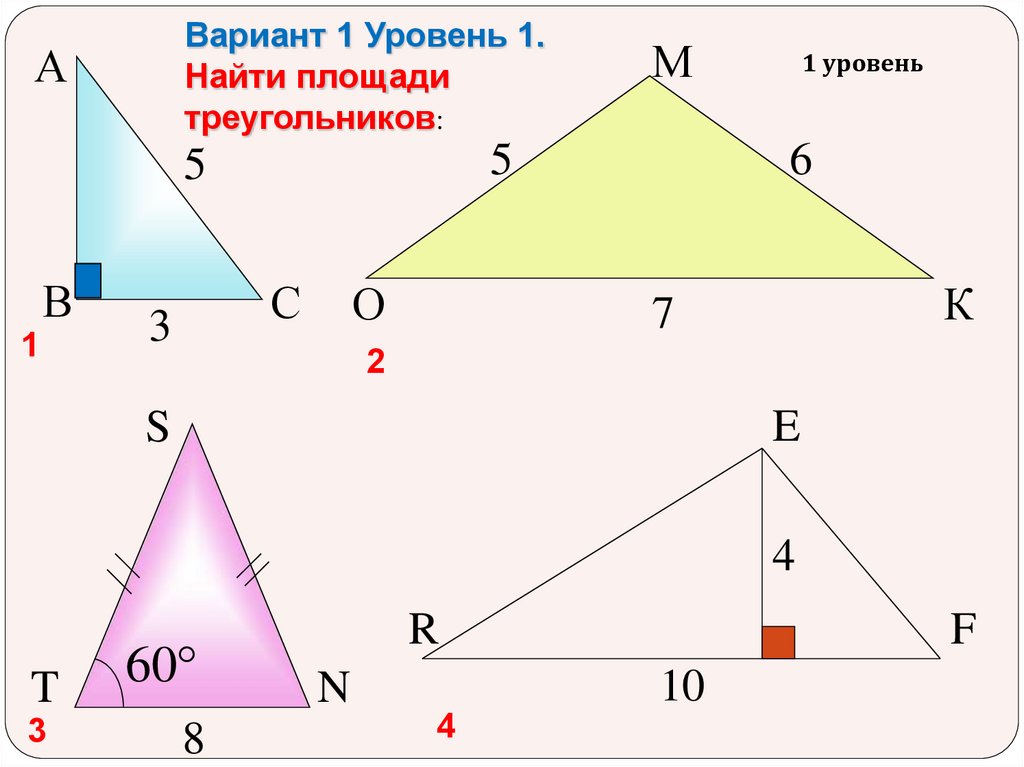
Вариант 1 Уровень 1.
Найти площади
треугольников:
А
5
5
В
1
С
3
М
О
1 уровень
6
К
7
2
E
S
4
T
3
60°
8
R
F
10
N
4