Закон рациональности отношений параметров граней (закон целых чисел). Лекция 7

1.

2.

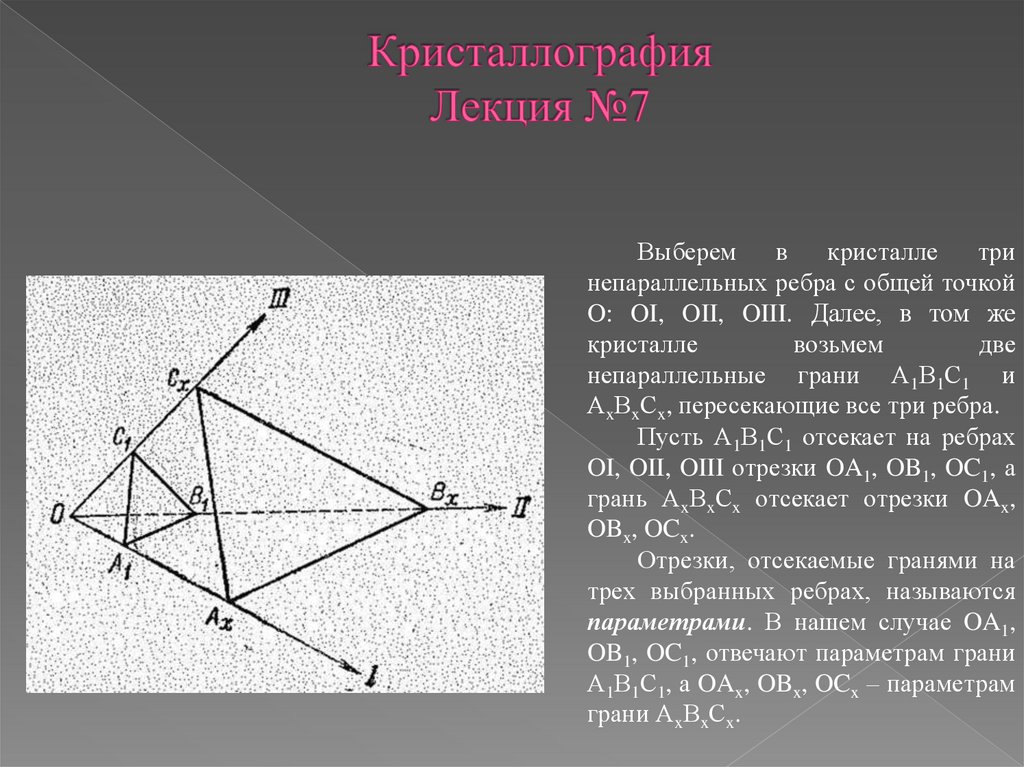
Выберем
в
кристалле
три
непараллельных ребра с общей точкой
O: OI, OII, OIII. Далее, в том же
кристалле
возьмем
две
непараллельные грани А1В1С1 и
АxВxСx, пересекающие все три ребра.
Пусть А1В1С1 отсекает на ребрах
OI, OII, OIII отрезки OA1, OB1, OC1, а
грань АxВxСx отсекает отрезки OAx,
OBx, OCx.
Отрезки, отсекаемые гранями на
трех выбранных ребрах, называются
параметрами. В нашем случае OA1,
OB1, OC1, отвечают параметрам грани
А1В1С1, а OAx, OBx, OCx – параметрам
грани АxВxСx.

3.

OAx OBx OCx
:
:
= p: q: r
OA1 OB1 OC1
где р, q, r – целые и обычно небольшие числа.
Такова сущность закона рациональных отношений параметров грани (закона целых
чисел) Гаюи: двойные отношения параметров, отсекаемых двумя любыми гранями
кристалла на трех пересекающихся ребрах его, равны отношениям целых и сравнительно
малых чисел.

4.

Некоторую
грань
А1В1С1,
пересекающую все три координатные оси,
возьмем в качестве единичной (масштабной)
грани. Единичная грань – грань кристалла,
параметры которой приняты за единицы
измерения. Отрезок OA1 служит масштабом
(единицей) для первой оси X (OI). Отрезок
OB1 служит масштабом для второй оси Y
(ОII). Отрезок ОС1 соответствует масштабу
для третьей оси Z (ОIII). Если задана
некоторая грань АxВxСx, то согласно закону
целых чисел, имеем
OAx OBx OCx
:
:
= p: q: r
OA1 OB1 OC1
где р, q, r – целые и обычно небольшие
числа.

5.

Однако для числовой характеристики грани АxВxСx во многих отношениях удобнее
брать обратные величины:
OA1 OB1 OC1
:
:
OAx OBx OCx
Эти отношения отвечают символу грани АxВxСx. Приведя дроби к общему
знаменателю и взяв отношение между ними (отбросив знаменатели и сократив, если
можно, на общего множителя), получим здесь также три целых числа:
OA1 OB1 OC1
:
:
= h: k: l
OAx OBx OCx
где h, k, l – целые и обычно небольшие числа.

6.

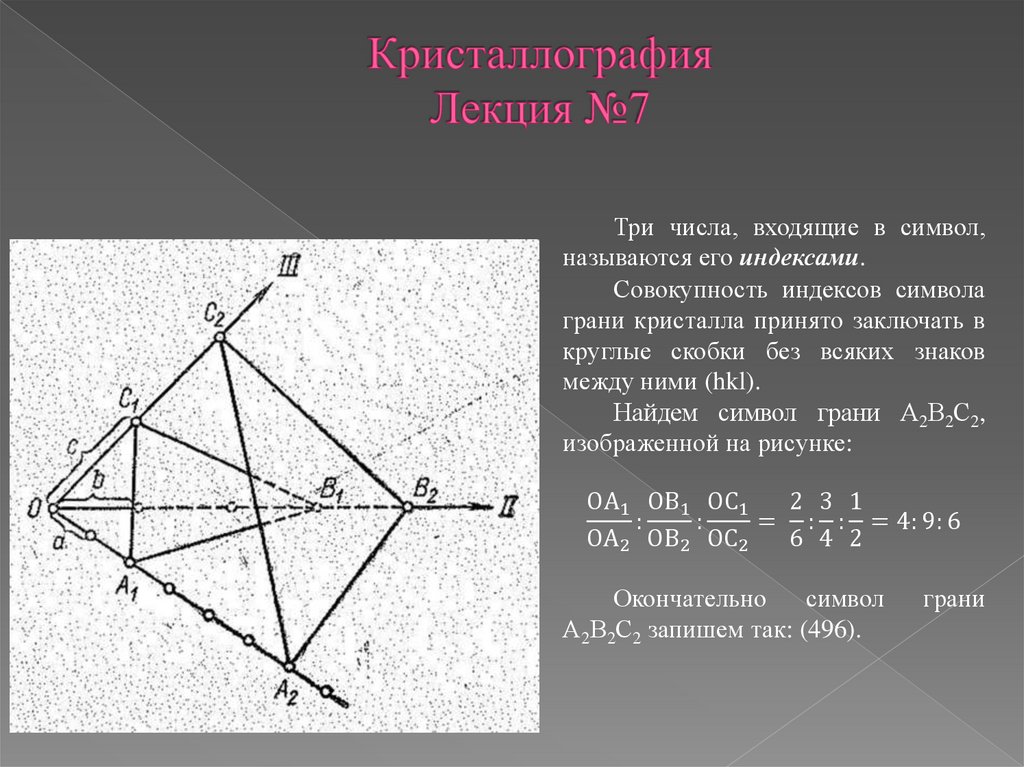
Три числа, входящие в символ,
называются его индексами.
Совокупность индексов символа
грани кристалла принято заключать в
круглые скобки без всяких знаков
между ними (hkl).
Найдем символ грани А2В2С2,
изображенной на рисунке:
OA1 OB1 OC1
2 3 1
:
:
= : : = 4: 9: 6
OA2 OB2 OC2
6 4 2
Окончательно
символ
А2В2С2 запишем так: (496).
грани

7.

Для получения символов граней необходимо за координатные оси принять три
направления, проходящие через одну точку и параллельные трем ребрам кристалла, а
также выбрать единичную грань.
Направления в кристалле, параллельные его ребрам и принятые за координатные оси,
называются кристаллографическими осями.
Выбор кристаллографических осей и единичной грани называется установкой
кристалла.
В общем случае первая кристаллографическая ось направляется к наблюдателю,
вторая лежит более или менее горизонтально и параллельно наблюдателю, третья
ориентируется вертикально.
Для первой оси отрезки, отсекаемые гранями на передней ее части (до точки О),
считаются положительными, на задней – отрицательными. Для второй оси отрезки справа
положительные, слева отрицательные. Для третьей оси выше О имеем положительные, а
ниже отрицательные отрезки.

8.

1) Символ (111) всегда отвечает единичной грани.
Действительно, при определении символа единичной грани, вместо OAx, OBx, OCx в
выражение
OA1 OB1 OC1
:
:
OAx OBx OCx
приходится подставлять ее же параметры (OA1, OB1, OC1).
В результате получаем
OA1 OB1 OC1
:
:
= 1: 1: 1
OA1 OB1 OC1
Следовательно, символ (111) всегда выражает единичную грань, несмотря на то, что в
общем случае единичные отрезки на трех кристаллографических осях не равны друг другу.

9.

2) В символе грани, параллельной какой-либо кристаллографической оси, индекс,
соответствующий этой оси, равен нулю.
Пусть грань АxВxСx параллельна первой кристаллографической оси. Тем самым ее
отрезок по оси X равен бесконечности (ОАх = ∞).
Подставив значение ОАх в общее выражение для символов, находим
OA1 OB1 OC1
OA1 OB1 OC1
OB1 OC1
:
:
=
:
:
= 0:
:
OAx OBx OCx
∞ OBx OCx
OBx OCx
Аналогично находим символы грани, параллельной второй кристаллографической оси
OA1
OC1
:
0:
OA
OC
x
x
OA
OB
и грани, параллельной третьей кристаллографической оси OA1 : OB1 : 0
x
x

10.

Грань, пересекающая первую кристаллографическую ось и параллельная двум другим,
всегда имеет символ (100):
OA1 OB1 OC1 OA1 OB1 OC1 OA1
:
:
=
:
:
=
: 0: 0 = 1: 0: 0
OAx OBx OCx OAx ∞ ∞
OAx
Соответственно
грань,
пересекающая
вторую
кристаллографическую
ось
и
параллельная двум другим, обладает символом (010). Наконец, грань, параллельная первой
и второй кристаллографическим осям и пересекающая лишь третью, получает символ
(001).

11.

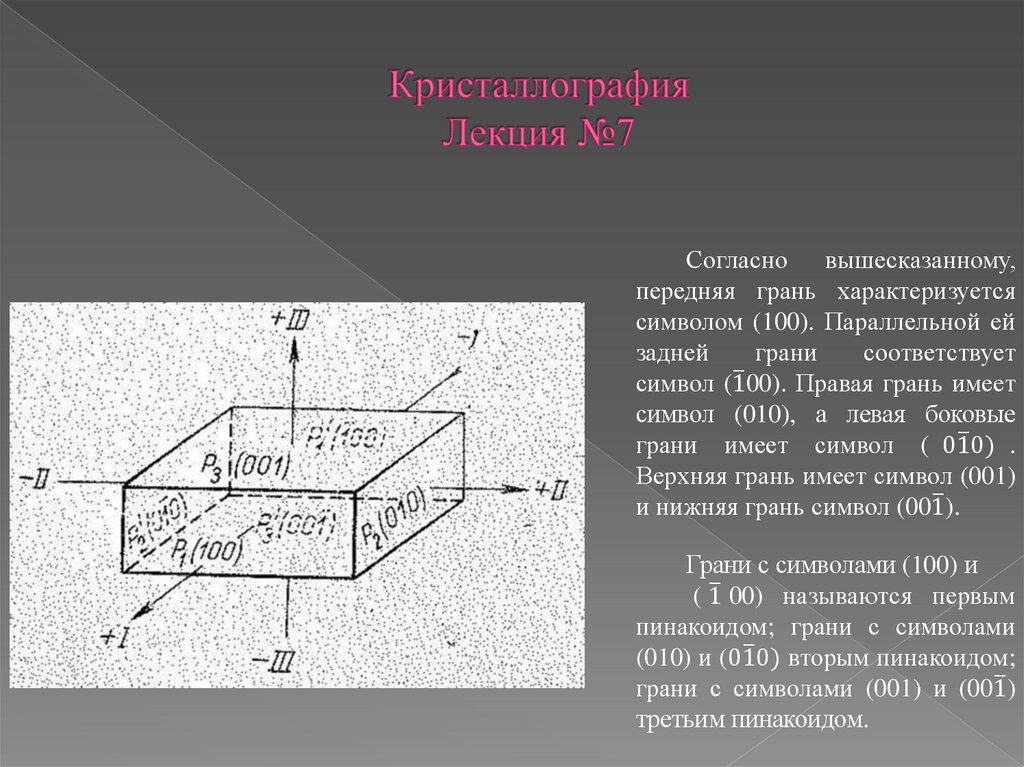
Согласно вышесказанному,
передняя грань характеризуется
символом (100). Параллельной ей
задней
грани
соответствует
ത
символ (100).
Правая грань имеет
символ (010), а левая боковые
ത
грани имеет символ ( 010)
.
Верхняя грань имеет символ (001)
и нижняя грань символ (001ത ).
Грани с символами (100) и
( 1ത 00) называются первым
пинакоидом; грани с символами
ത вторым пинакоидом;
(010) и (010)
ത
грани с символами (001) и (001)
третьим пинакоидом.

12.

Теорема 1. Оси симметрии L2, L3, L4, L6, либо совпадают с рядами решеток, либо
параллельны им и, следовательно, являются действительными или возможными ребрами
кристаллов. Следствие. Кристаллографические оси можно совмещать с осями симметрии,
так как последние соответствуют действительным или теоретически возможным ребрам
кристаллов.
Теорема 2. Нормали к плоскостям симметрии либо совпадают с рядами
пространственных решеток, либо параллельны им и, следовательно, являются
действительными
или
возможными
ребрами
кристаллов.
Следствие.
Кристаллографические оси можно совмещать с нормалями к плоскостям симметрии,
поскольку эти нормали параллельны действительным или возможным ребрам кристаллов.
На основании двух приведенных теорем кристаллографические оси проводятся:
1) по осям симметрии,
2) по нормалям к плоскостям симметрии (в случае отсутствия или недостаточного
числа осей),
3) параллельно действительным или возможным ребрам кристаллов (в случае
отсутствия или недостаточного числа осей и плоскостей симметрии).