Похожие презентации:
Делимость натуральных чисел
1. Делимость натуральных чисел
2. Натуральными числами называют
числа, используемые для счетаN
множество
натуральных чисел
Z
множество целых
чисел
Целыми числами называют
натуральные числа , им
противоположные и ноль
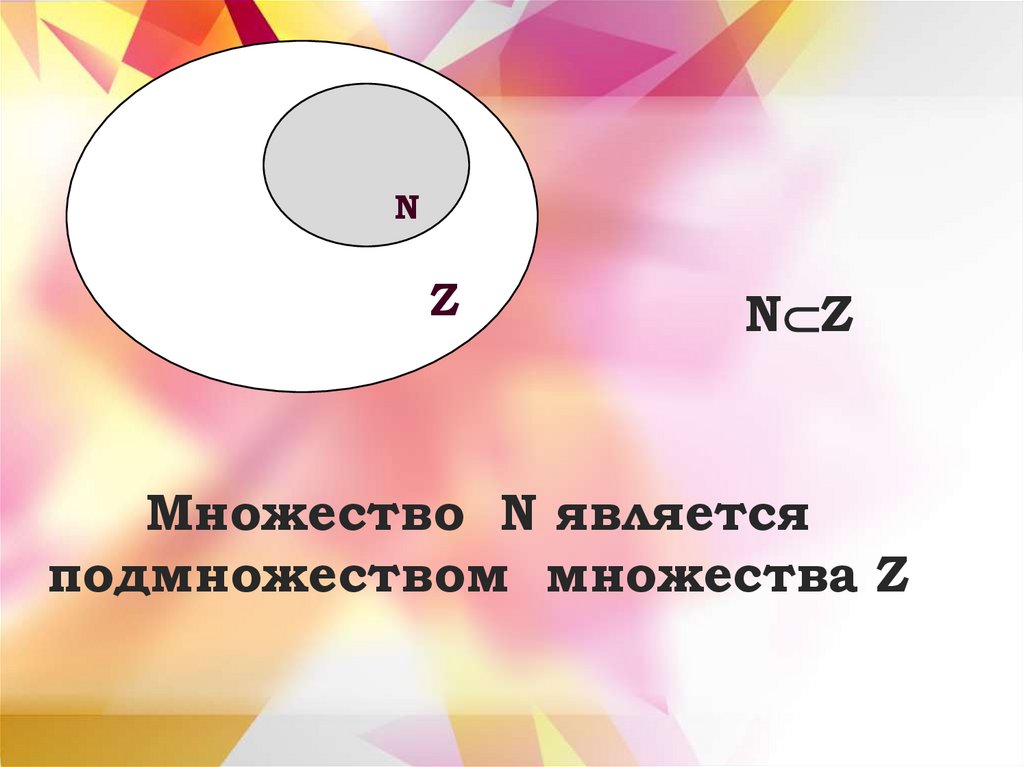
3. NZ
NZ
N Z
Множество N является
подмножеством множества Z
4. Определение. Пусть даны два натуральных числа – a и b. Если существует такое натуральное число q такое, что выполняется
равенствоa=bq, то говорят, что число a
делится нацело на число b. При этом
число a называют делимым, b –
делителем, q- частным. Число a
называют также кратным числа b.
a
b
«a делится на b нацело»
5. Свойство 1.
Если a c и c b, то a b.48 6 и 6 3, значит, 48 3
Свойство 2.
Если a b и c b, то (a+c) b.
12 3 и 15 3, значит, (12+15) 3
6. Свойство 3.
Если a b и c не делится на b,то (a+с) не делится на b.
48 6 и 7 не делится на 6,
значит, (48+7) не делится на 6
Свойство 4.
Если a b и (а+c) b, то c b.
12 3 и (12+6) 3, значит, 6 3
7. Свойство 5.
Если a b и c d , то aс bd.48 6 и 9 3, значит, (48·9) (6·3)
Свойство 6.
Если a b, с –любое натуральное
число, то аc bс; если ас bс, то а b.
12 3,
значит, (12·4) (3·4)
8. Свойство 9.
Средип последовательных
(n-2)(n-1)n(n+1)(n+2)
чисел
одно и произведение
только одно
При
n>2 имеем
делится на п. чисел,
пяти последовательных
Прииз
n=1,
n=2 произведение
одно
которых,
по свойству 9,
Побращается
ример.
в ноль, на
значит,
обязательно
делится
5, хотя
делится
Доказать,
что
любого
бы
одно –на
на2,3,4,5,8
3,для
хотя
бы одно –
натурального
числа песть
число
на 4 и обязательно
ещё
хотя бы одно
четное,на
которое
делится
2,3,4,5,8
делится на 2. По свойству 5 и 7,
произведение делится на
2,3,4,5, то есть делится на 8







 Математика
Математика