Графы

1. ГРАФЫ

2.

Граф – это совокупность точек, соединенных
между собой линиями.
Граф служит для наглядного представления
связей между объектами.
Это замечательные математические объекты, с их помощью
можно решать очень много различных, внешне не похожих
друг на друга задач.

3.

Леонард Эйлер (1707-1783)швейцарский, немецкий и
российский математик,
механик, внесший
фундаментальный вклад в
развитие науки.
Ему принадлежит первая
работа по теории графов,
хотя понятие “граф”
впервые было введено
венгерским математиком
Денешем Кенигом.

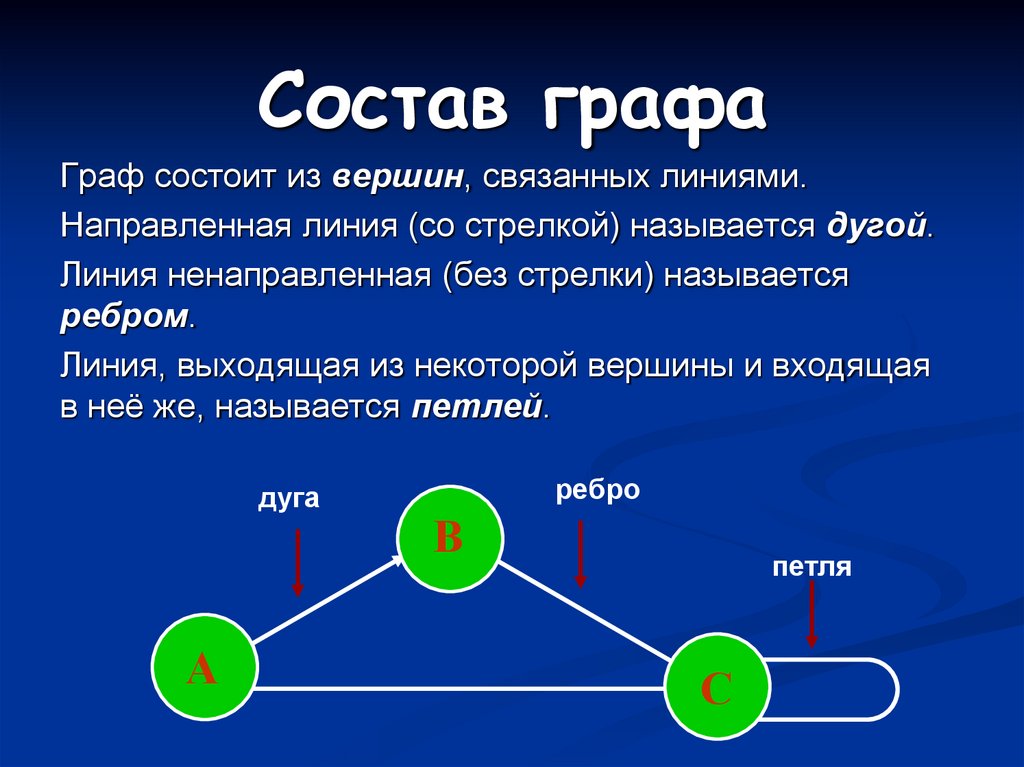
4. Состав графа

Граф состоит из вершин, связанных линиями.
Направленная линия (со стрелкой) называется дугой.
Линия ненаправленная (без стрелки) называется
ребром.
Линия, выходящая из некоторой вершины и входящая
в неё же, называется петлей.
дуга
А
ребро
В
петля
С

5.

Узлы графа
– объекты или вершины,
представленные в виде точек
Дуги или рёбра – это линии связи или пути между
объектами.

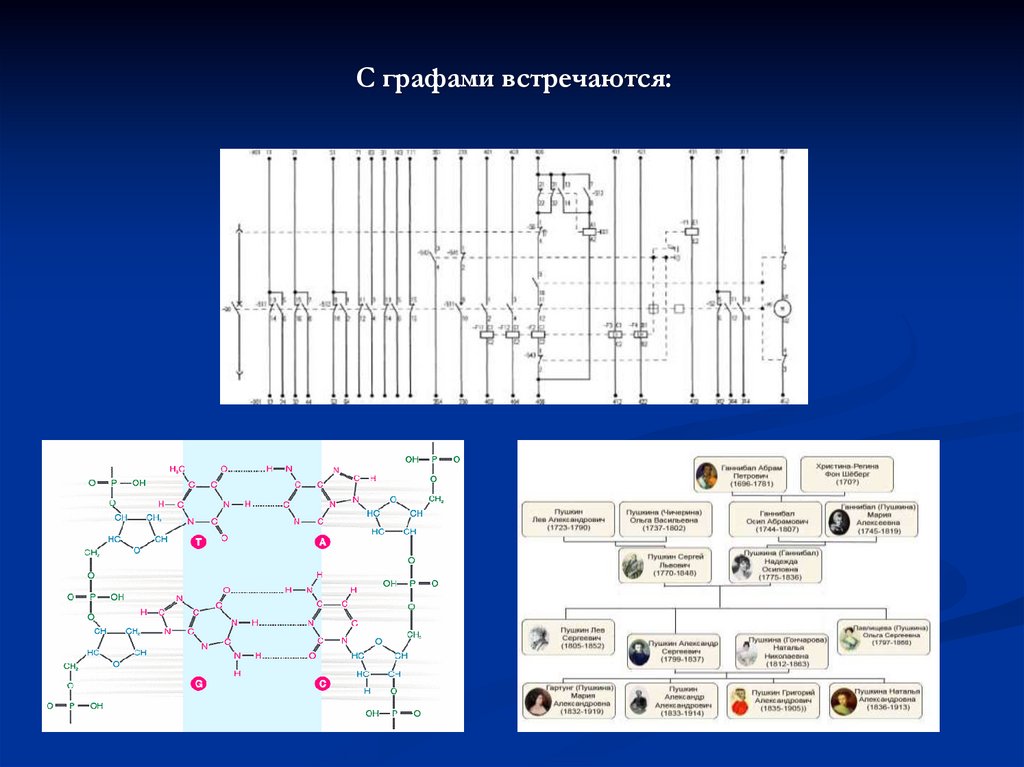
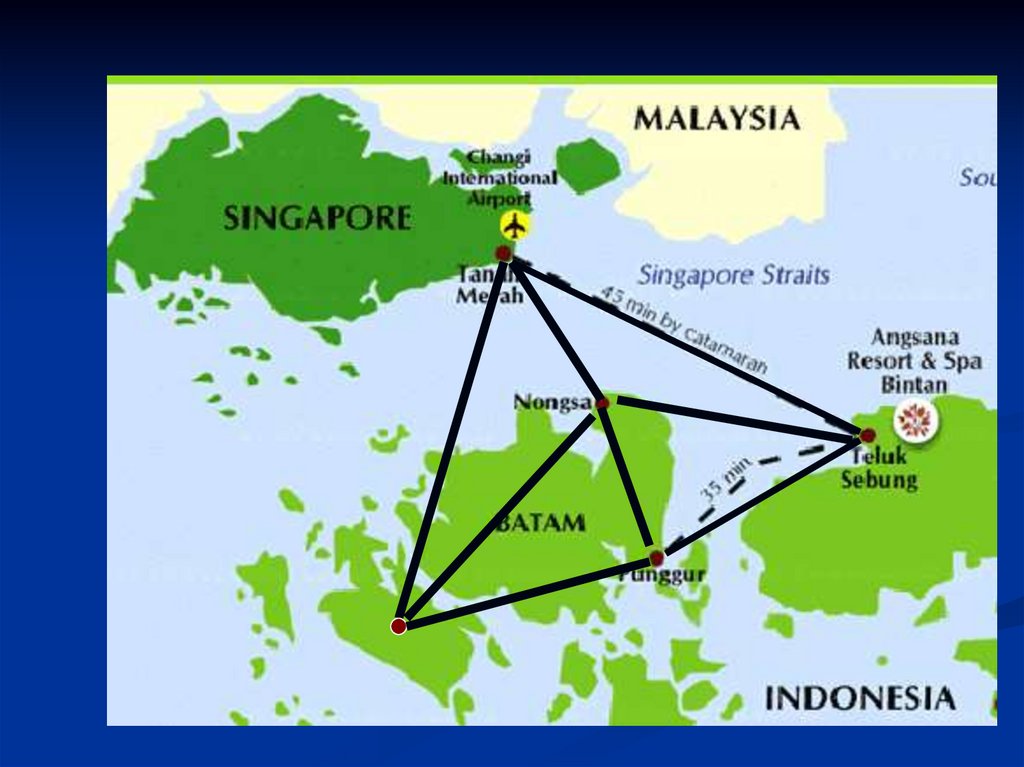
6. С графами встречаются:

7. Схема Метро

8.

9.

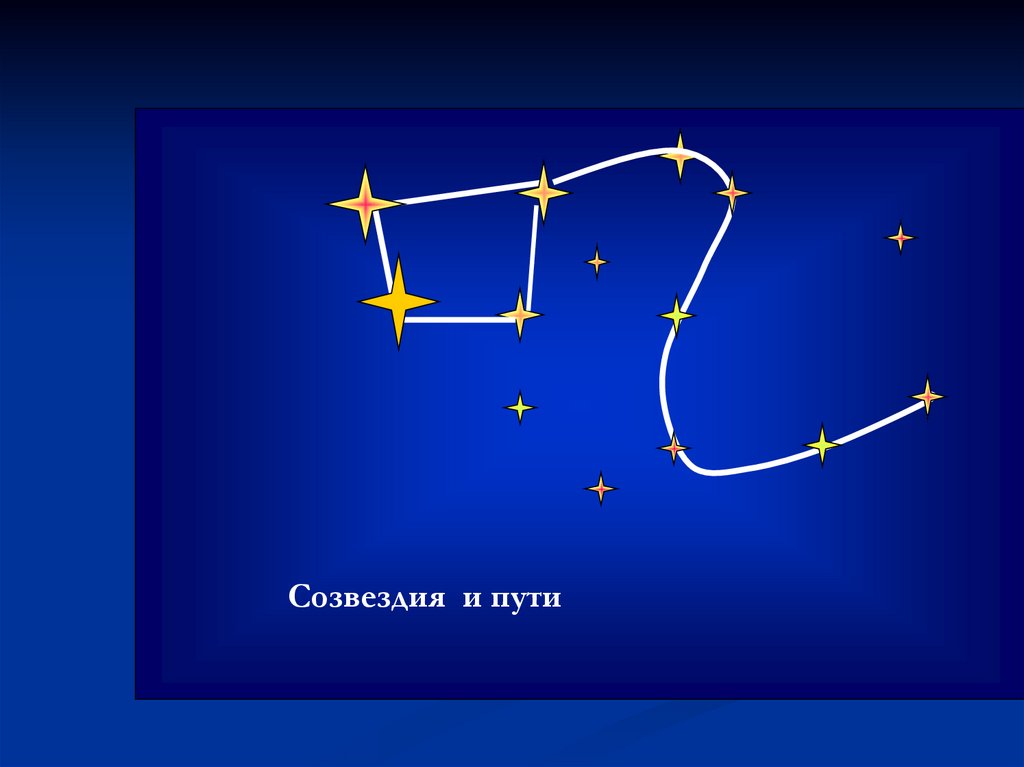
Созвездия и пути

10. Виды графов:

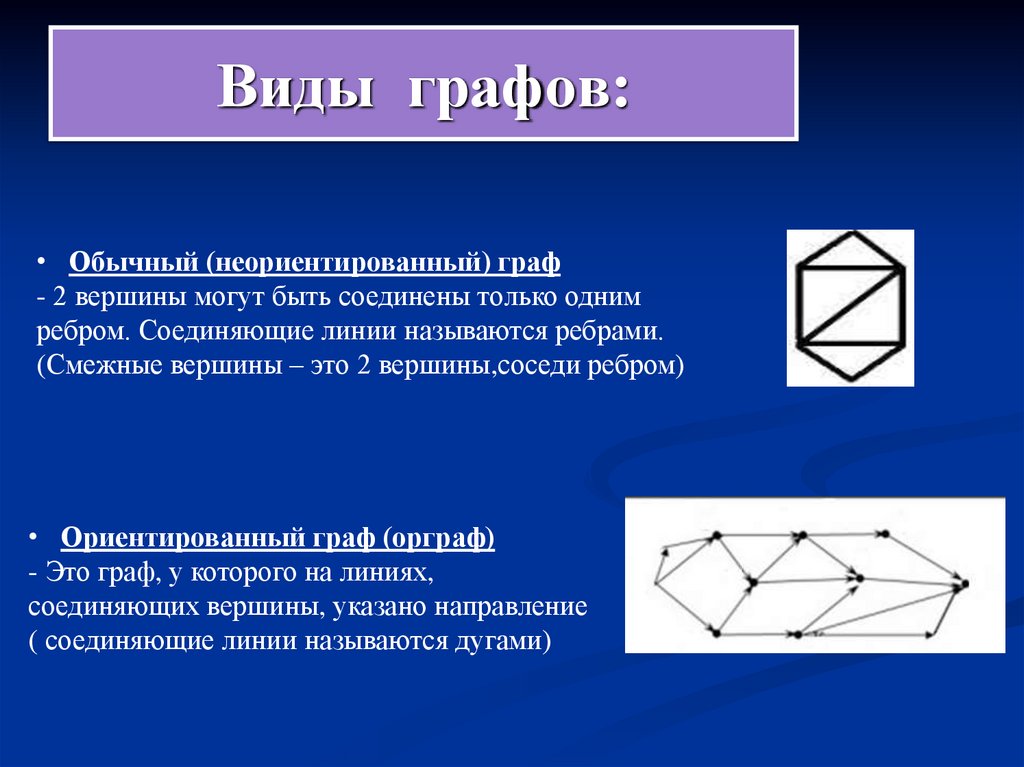
• Обычный (неориентированный) граф
- 2 вершины могут быть соединены только одним
ребром. Соединяющие линии называются ребрами.
(Смежные вершины – это 2 вершины,соседи ребром)
• Ориентированный граф (орграф)
- Это граф, у которого на линиях,
соединяющих вершины, указано направление
( соединяющие линии называются дугами)

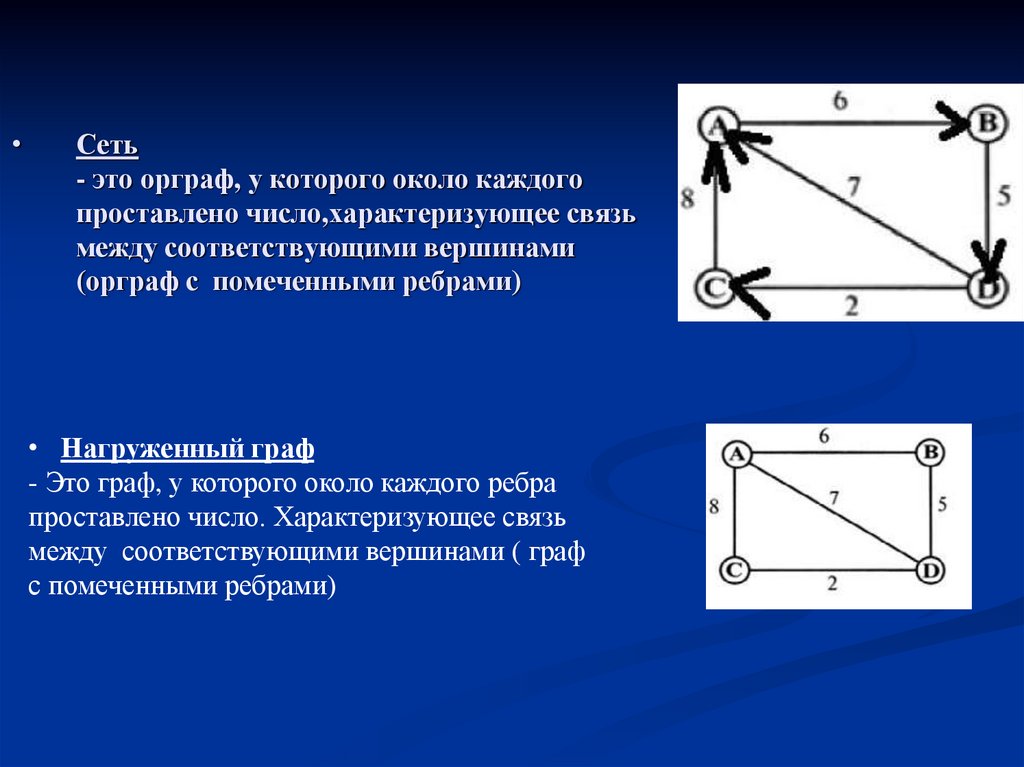
11. Сеть - это орграф, у которого около каждого проставлено число,характеризующее связь между соответствующими вершинами (орграф с

Сеть
- это орграф, у которого около каждого
проставлено число,характеризующее связь
между соответствующими вершинами
(орграф с помеченными ребрами)
• Нагруженный граф
- Это граф, у которого около каждого ребра
проставлено число. Характеризующее связь
между соответствующими вершинами ( граф
с помеченными ребрами)

12. Свойства графов:

• Для любого графа сумма степеней
вершин равна удвоенному количеству
ребер
• Для любого графа количество вершин
нечетной степени всегда четно (аналог
задачи: в любой момент времени
количество людей, сделавших нечетное
количество рукопожатий,четно)
• В любом графе есть по крайней мере 2
вершины, имеющие одинаковую
степень.

13.

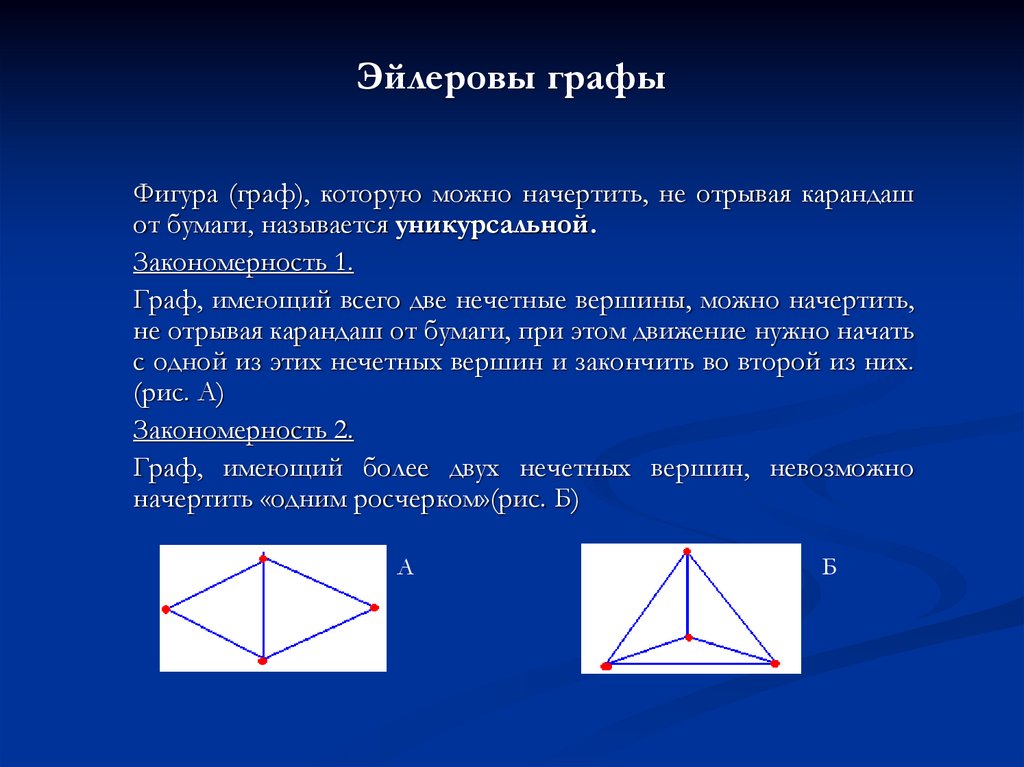
Эйлеровы графы
Фигура (граф), которую можно начертить, не отрывая карандаш
от бумаги, называется уникурсальной.
Закономерность 1.
Граф, имеющий всего две нечетные вершины, можно начертить,
не отрывая карандаш от бумаги, при этом движение нужно начать
с одной из этих нечетных вершин и закончить во второй из них.
(рис. А)
Закономерность 2.
Граф, имеющий более двух нечетных вершин, невозможно
начертить «одним росчерком»(рис. Б)
А
Б

14.

Закономерность 3.
Если все вершины графа четные, то можно не отрывая карандаш
от бумаги, проводя по каждому ребру только один раз, начертить
этот граф. Движение можно начать с любой вершины и закончить
его в той же вершине.

15.

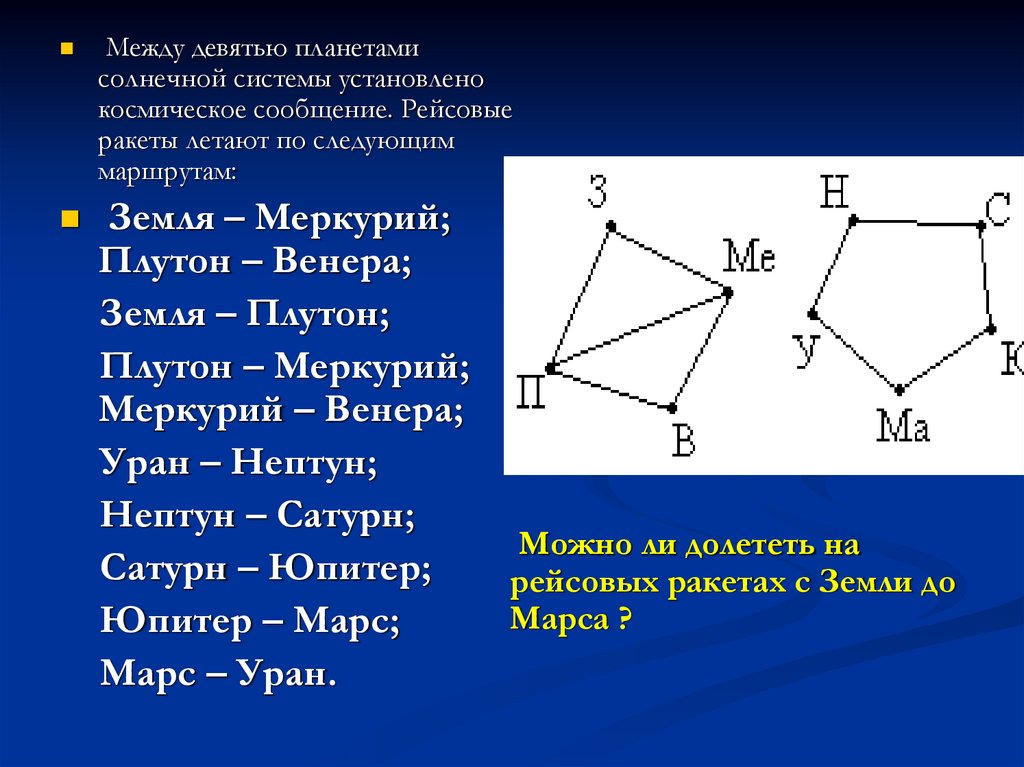
Между девятью планетами
солнечной системы установлено
космическое сообщение. Рейсовые
ракеты летают по следующим
маршрутам:
Земля – Меркурий;
Плутон – Венера;
Земля – Плутон;
Плутон – Меркурий;
Меркурий – Венера;
Уран – Нептун;
Нептун – Сатурн;
Сатурн – Юпитер;
Юпитер – Марс;
Марс – Уран.
Можно ли долететь на
рейсовых ракетах с Земли до
Марса ?

16.

Решение: Нарисуем схему условия: планеты
изобразим точками, а маршруты ракет –
линиями.
Теперь сразу видно, что долететь с Земли
до Марса нельзя.

17.

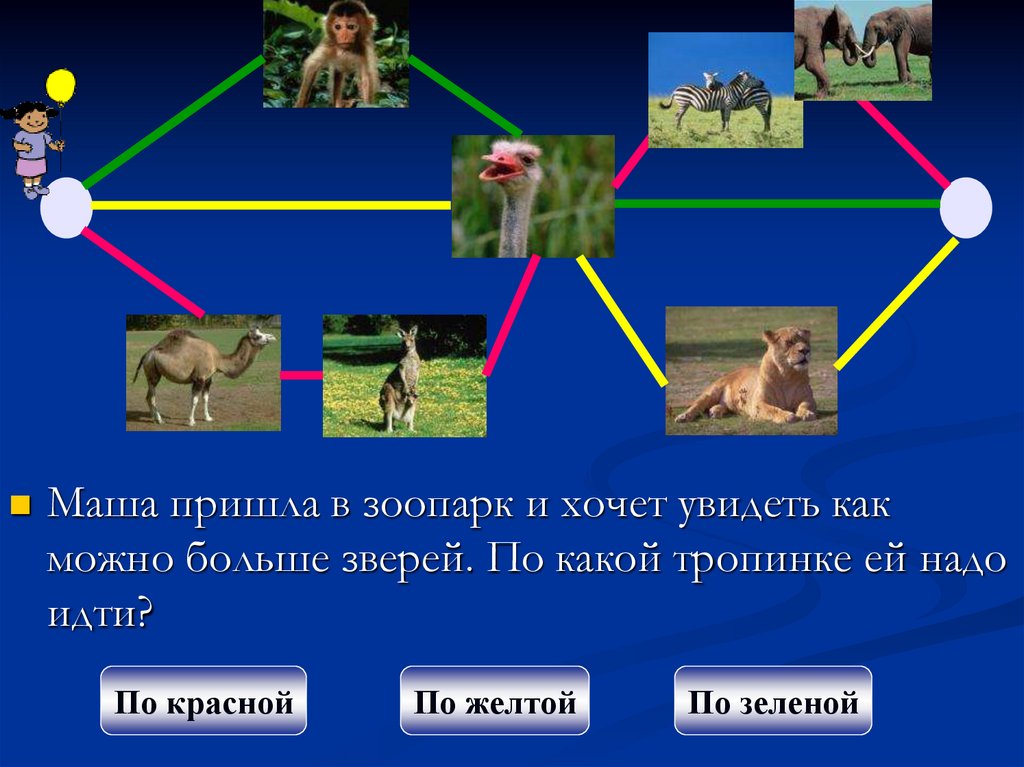
Маша пришла в зоопарк и хочет увидеть как
можно больше зверей. По какой тропинке ей надо
идти?
По красной
По желтой
По зеленой

18.

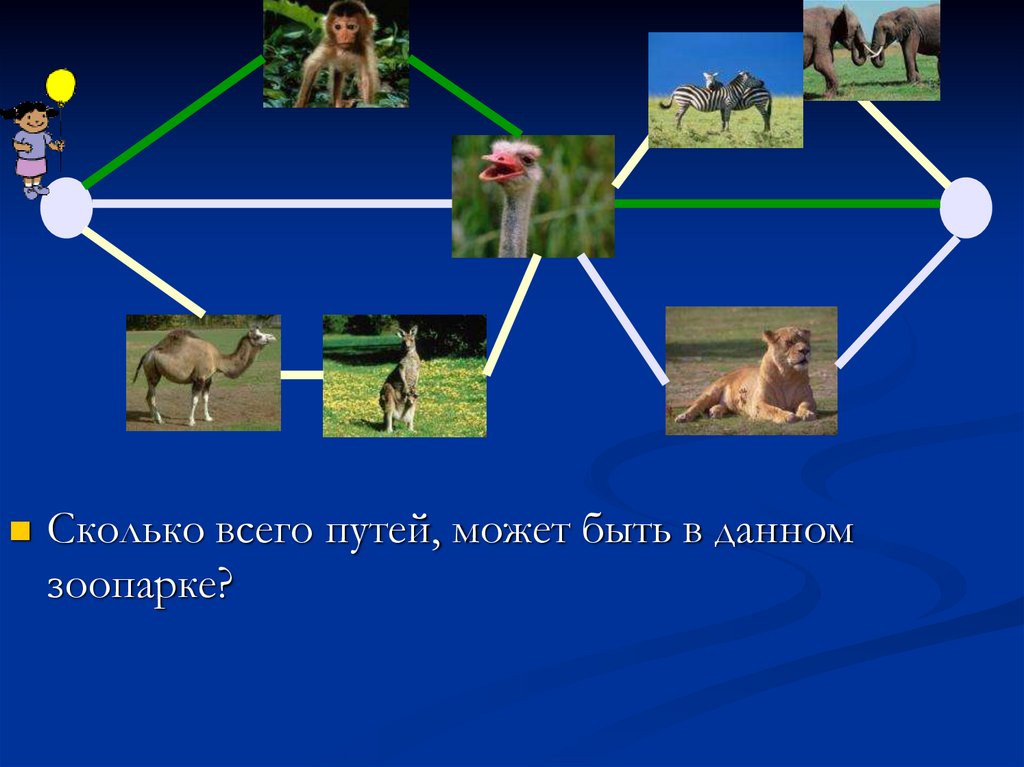
Сколько всего путей, может быть в данном
зоопарке?

19.

Д
А
Б
Г
В
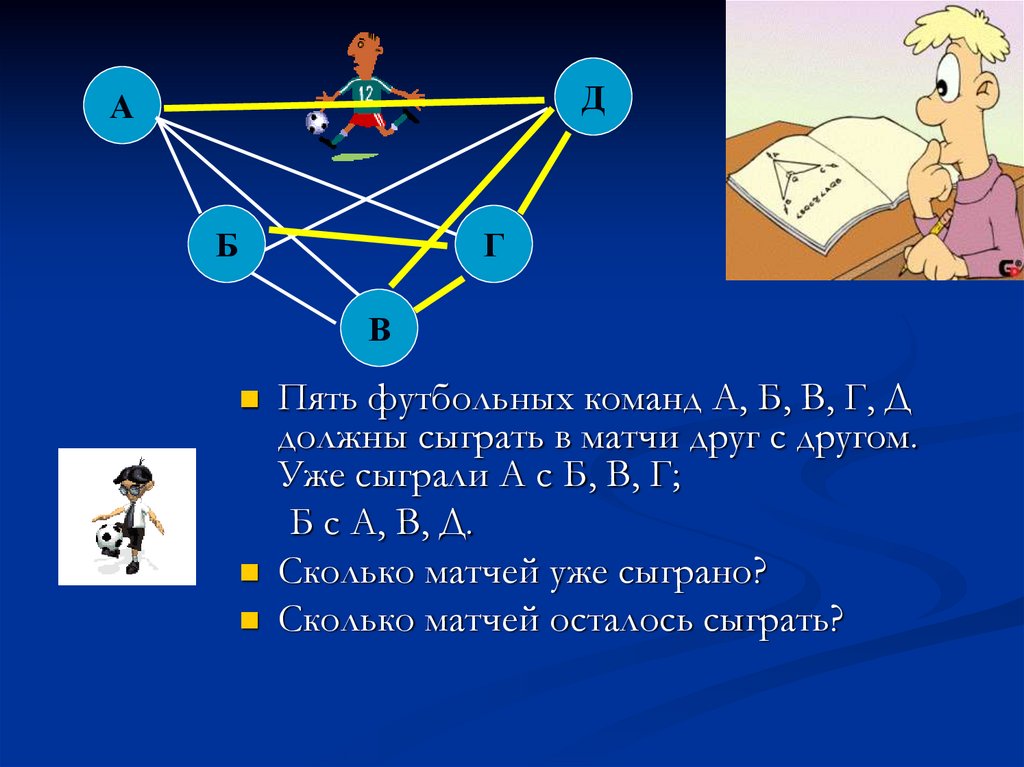
Пять футбольных команд А, Б, В, Г, Д
должны сыграть в матчи друг с другом.
Уже сыграли А с Б, В, Г;
Б с А, В, Д.
Сколько матчей уже сыграно?
Сколько матчей осталось сыграть?

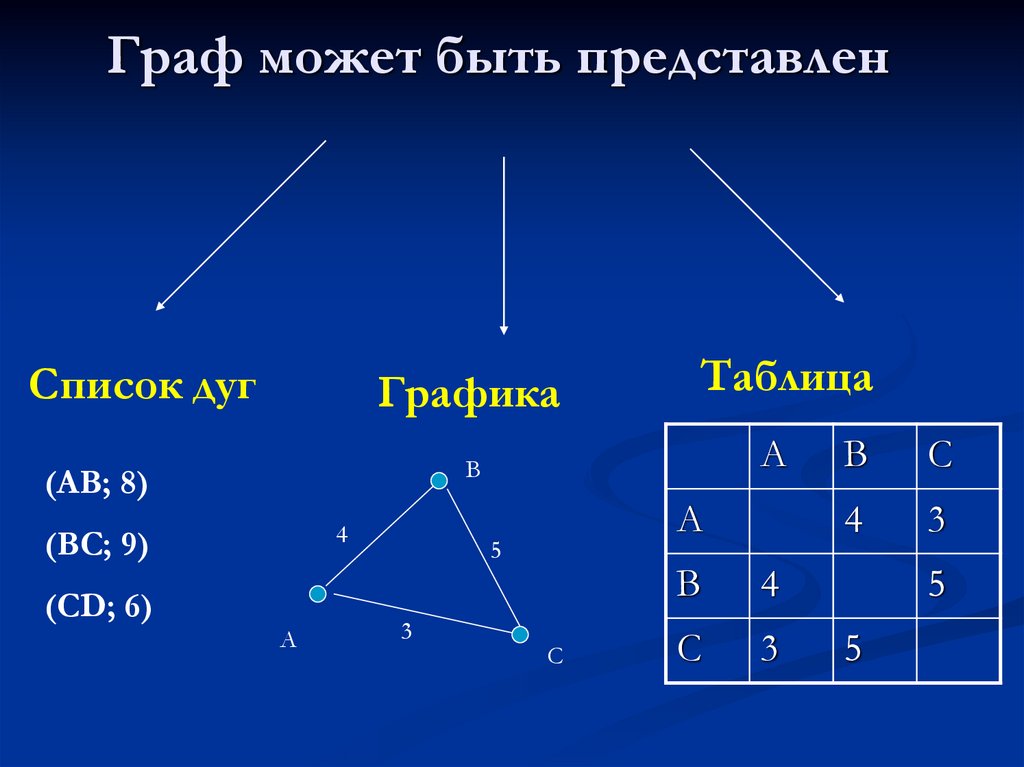
20. Граф может быть представлен

Список дуг
Графика
А
В
(АВ; 8)
4
(ВС; 9)
(СD; 6)
Таблица
А
А
5
3
С
В
4
С
3
В
С
4
3
5
5

21.

Между населёнными пунктами А, В, С, D, E построены дороги, протяженность
которых приведена в таблице.
А
A
B
C
D
E
B
1
C
1
1
2
1
2
D
E
2
1
2
1
Определите кратчайшей путь между пунктами А и С. Передвигаться
можно только по построенным дорогам.

22.

На схеме нарисованы дороги между четырьмя населёнными
пунктами A, B, C, D и указаны протяжённости данных дорог.
Создайте таблицу по данной схеме.
Определите кратчайшее расстояние между пунктами А и С (при
условии, что передвигаться можно по указанным на схеме дорогам).
3
А
6
4
B
1
C
D
1

23.

1. В таблице приведена стоимость перевозок между соседними
железнодорожными станциями. Числа, стоящие на пересечениях строк и
столбцов означают стоимость проезда между соответствующими
соседними станциями. Если пересечение строки и столбца пусто, то
станции не являются соседними. Укажите схему, соответствующую
таблице.
А
А
В
1
С
4
A
4
1
4
1
2
2
A
C
1
E
A 4
B
3
C
1
3
D
4
D
1
A
1
B
D
1
4
3
E
1
1
2
E
2
C
Е
D
3
E
B
С
3
D
1
В
C
1
2
B
2
D
3
E