Определение класса точности прибора

1.

ТЕМА:
Определение класса
точности прибора

2.

Цель: научиться определять
погрешности измерений по
классу точности прибора и
находить цену деления.

3.

Точность измерений
Точность измерения – это степень
приближения результатов измерения
к некоторому действительному
значению физической величины.
Чем меньше точность, тем больше
погрешность измерения и, соответственно,
чем меньше погрешность, тем выше
точность.

4.

Погрешностью измерения называют
отклонение результата измерения от
истинного или действительного значения
измеряемой величины.
Δ Хизм = Х - Хд
Погрешности могут быть:
• систематические,
• случайные,
• грубые.

5.

6.

Используется
для измерения
магнитного
потока, а так
же для
измерения
магнитной
индукции.

7.

8.

Задача 1.
Микроамперметр на 100 мкА имеет шкалу в 200 делений.
Определить цену деления и показания прибора? Показания
прибора 120 делений.
Задача 2.
Фазометр на 20 Ф имеет шкалу в 50 делений. Определить цену
деления и показания прибора? Показания прибора 42 деления.

9.

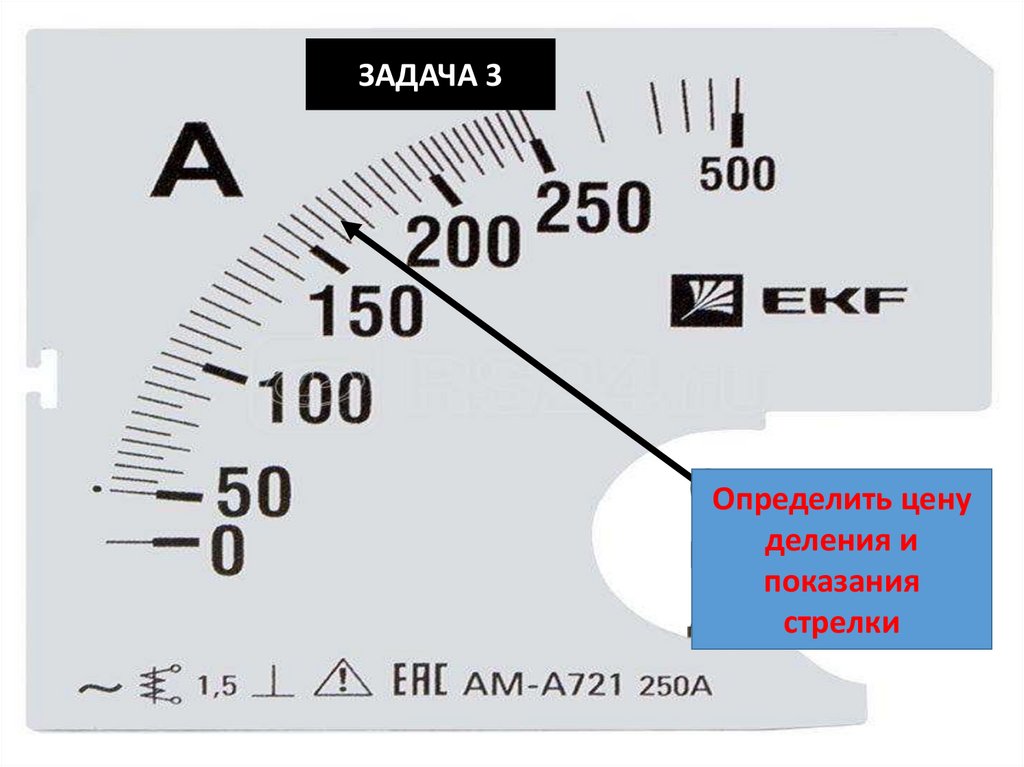
ЗАДАЧА 3
Определить цену
деления и
показания
стрелки

10.

Задача 4.
Миллиамперметр.
Определить цену
деления и показания
прибора? Показания
прибора 12 делений.

11.

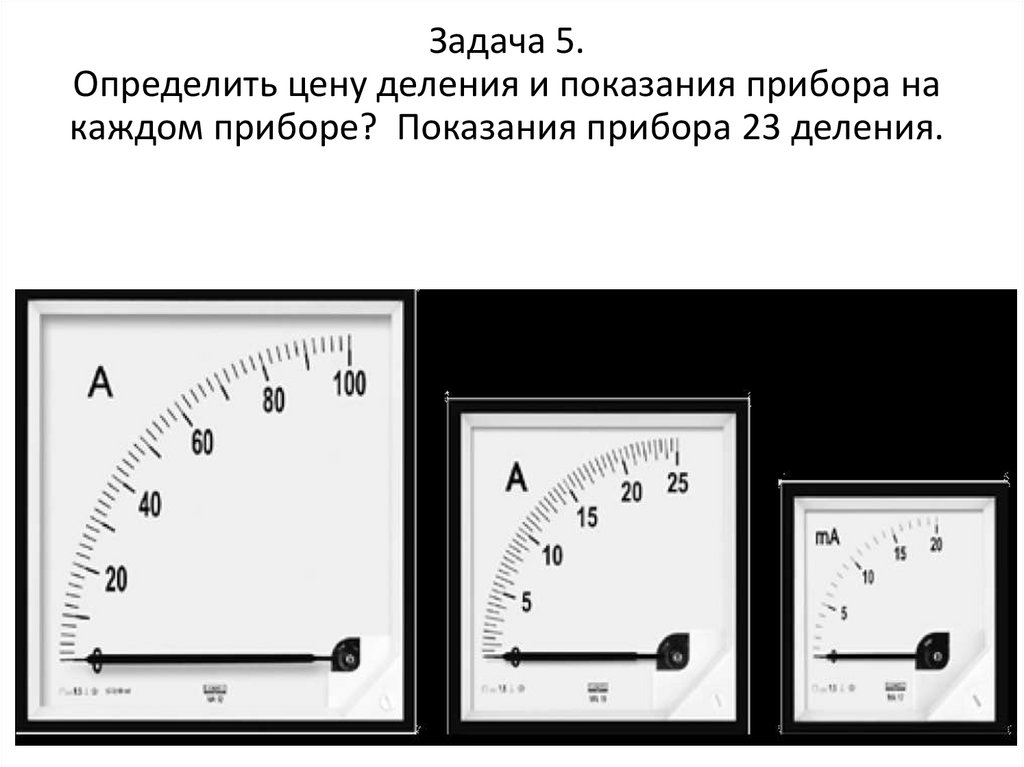
Задача 5.
Определить цену деления и показания прибора на
каждом приборе? Показания прибора 23 деления.

12.

Задача 6. Найти цену деления и показания
прибора, при 26 делениях

13.

Погрешности:
►Абсолютная погрешность измерения (Δ)
представляет собой разность между измеренной
величиной и истинным или действительным
значением этой величины.
Δ = Х - Хи
►Относительная погрешность измерения (δ)
представляет собой отношение абсолютной
погрешности измерения к действительному значению
измеряемой величины.
(δ) = + Δ / Хи
(δ) = (+ Δ / Хи ) * 100

14.

► Приведенная погрешность измерения
представляет собой отношение абсолютной
погрешности к нормированному значению
величины
В отличие от относительной и приведенной
абсолютная погрешность всегда имеет ту же
размерность, что и измеряемая величина.

15.

При многократных измерениях
истинного значения, как правило,
используют среднее арифметическое
значение

16.

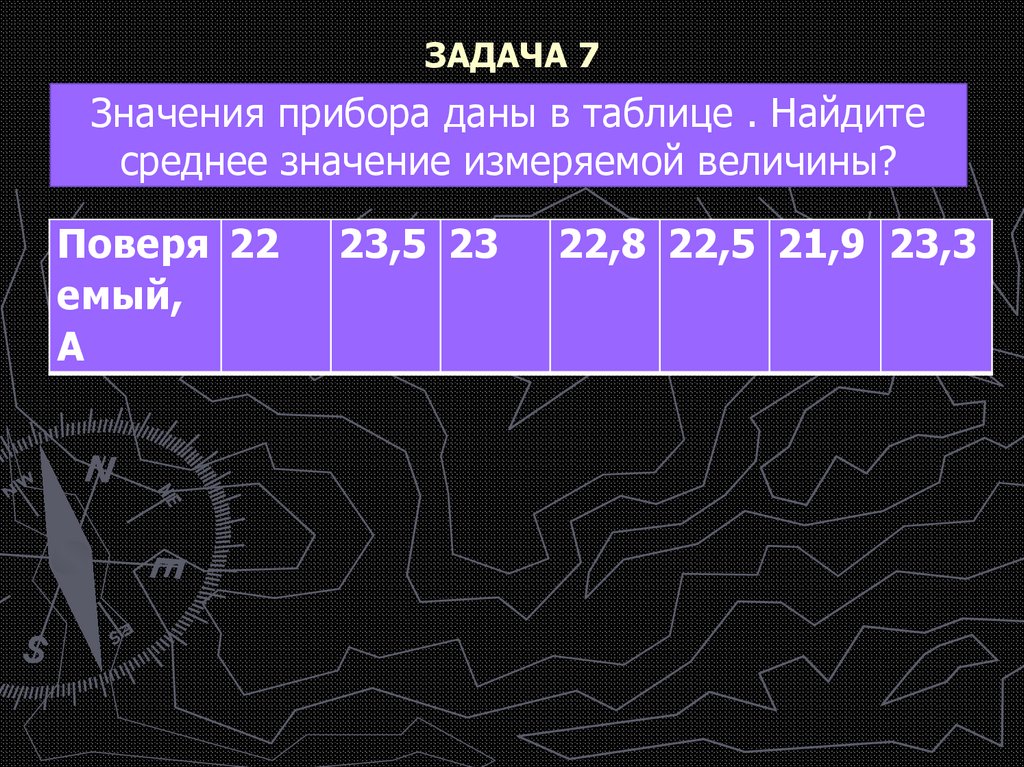
ЗАДАЧА 7
Значения прибора даны в таблице . Найдите
среднее значение измеряемой величины?
Поверя 22
емый,
А
23,5 23
22,8 22,5 21,9 23,3

17.

Основная нормируемая метрологическая
характеристика средств измерений — это
погрешность.
Основная погрешность — это погрешность
при нормальных условиях эксплуатации:
температура 20 ± 5 °С,
► относительная влажность воздуха 65 % при
температуре 20 °С,
► напряжение в сети питания 220 В с частотой 50 Гц,
► атмосферное давление от 97,4 до 104 кПа,
► отсутствие электрических и магнитных полей
(наводок).

18.

При технических измерениях, когда не
учитываются различные влияющие
дестабилизирующие факторы, как
правило, используется более грубое
нормирование — присвоение средству
измерения определенного класса
точности.

19.

Класс точности — это обобщенная
метрологическая характеристика,
определяющая различные свойства средства
измерения.
Классы точности присваивают средствам измерений
при их разработке по результатам государственных
приемочных испытаний.

20.

Классы точности средств
измерений, выраженные
через абсолютные
погрешности, обозначают
прописными буквами
латинского алфавита или
римскими цифрами.
Наиболее широкое
распространение получило
нормирование класса
точности по приведенной
погрешности.

21.

задания класса точности используется для
приборов с резко неравномерной шкалой.
Класс точности задается числом К,
подчеркнутым галочкой:
0,5
В этом случае нормируется
основная приведенная
погрешность в процентах от
длины шкалы.

22.

23.

ПРИМЕР
Определить для вольтметра с пределом
измерения 30 В класса
точности 0,5 относительную погрешность для
точек 5, 10, 15, 20, 25 и 30 В и наибольшую
абсолютную погрешность прибора.
По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30
В – измеренное значение электрической величины;
Uпр = 30 В – предел шкалы вольтметра.
Приведенная погрешность

24.

Наибольшая
вольтметра
абсолютная
погрешность
Относительная погрешность однократного
измерения
= 0,5·30/5=3,0
Относительная погрешность вольтметра для точек
Uизм = Ui,
В
δU, %
5
3,0
10
15
20
25
30

25.

Относительная погрешность вольтметра для точек
Uизм = Ui,
В
5
10
15
20
25
30
δU, %
3,0
1,5
1,0
0,75
0,6
0,5

26.

ЗАДАЧА 8
При
измерении
напряжения
двумя
параллельно
включенными вольтметрами их показания были: U1 = 29,2 В,
U2 = 30 В. Показания какого прибора точнее, если класс
точности КV1 = 2,5, КV2 = 1,0, а пределы измерения соответственно
равны Uпр1 = 30 В; Uпр2 = 150 В.
Наибольшая абсолютная
погрешность вольтметра:

27.

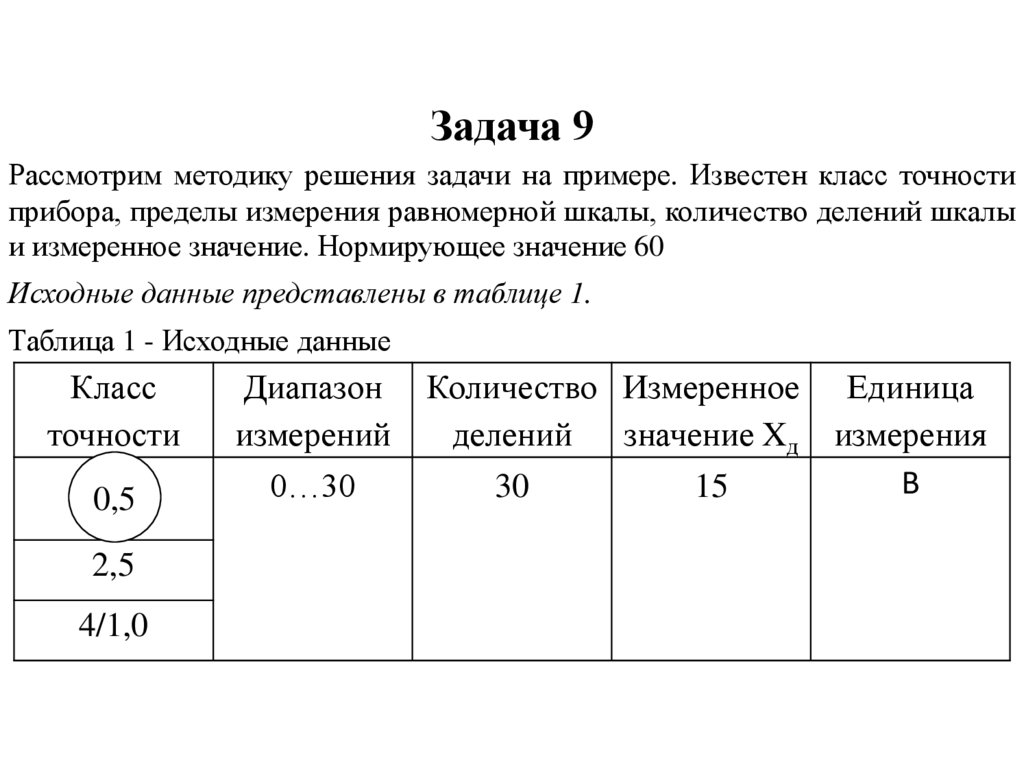
Пример решения задач
Рассмотрим методику решения задачи на примере. Известен класс точности
прибора, пределы измерения равномерной шкалы, количество делений шкалы
и измеренное значение. Нормирующее значение 50
Исходные данные представлены в таблице 1.
Таблица 1 - Исходные данные
Класс
точности
0,3
2,0
6/1,0
Диапазон
измерений
-25…25
Количество Измеренное
делений
значение Xд
25
16
Единица
измерения
°С

28.

Запишем данные
Таблица 2 - Структурные элементы и параметры шкалы прибора
СИ
Значение
Пределы измерений
От -25 до 25 ℃
Начальное (конечное)
значение шкалы
Начальное Xн=-25℃
Конечное Xк=+25℃
Цена деления шкалы
Сшк=50/25=2℃/дел
Чувствительность
S=25/50=0,5 дел/℃
Нормирующее значение
Количество делений
XN=50℃
25

29.

Определение погрешности измерения при различном
нормировании класса точности прибора
1. Для прибора класса точности
0,3
Относительная погрешность изменения δ=±0,3 %.
Определяем абсолютную погрешность измерения по формуле