Похожие презентации:
Основные понятия математической логики. Задание 15
1.
Задание 15Основные понятия математической логики.
Подтемы:
• Задачи с отрезками
• Задачи с множествами
• Задачи с делителями
• Задачи с побитовыми операциями
Уровень: Повышенный
Проверяется: Знание основных понятий и законов математической
логики
Примерное время на выполнение: 3 минуты
2.
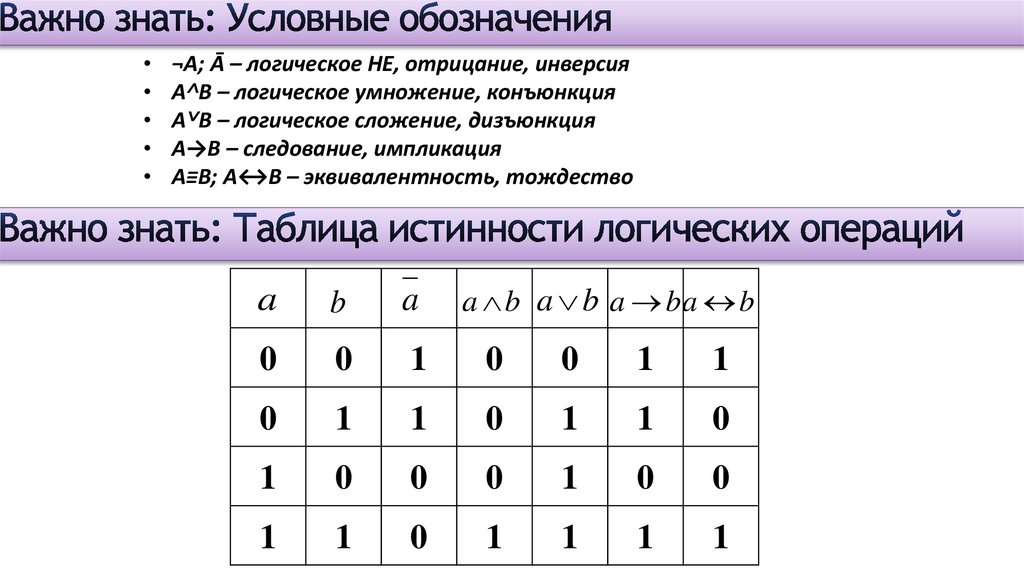
¬А; Ā – логическое НЕ, отрицание, инверсия
А˄В – логическое умножение, конъюнкция
А˅В – логическое сложение, дизъюнкция
А→В – следование, импликация
А≡В; А↔В – эквивалентность, тождество
a b a b a ba b
a
b
a
0
0
1
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
1
1
1
1
3.
Закон двойного отрицания:Закон де Моргана:
Импликация:
¬(¬A)=A
a b a b a b a b
a b a b a b a b
Эквивалентность (тождественность)
a b a b a b a b (a b) (a b) a b (a b) (b a )
a b a b a b
Упрощение выражений:
А˅А˄В=А (т.к. А˅А˄В=А˄1 ˅ А˄В=А ˄(1 ˅ В)=А˄1=А)
А˅(¬A)˄В=А˅В (т.к. А˅(¬A)˄В=(А˅(¬A)) ˄(А˅В)=1˄(А˅В)=А˅В
А→(В˄С)=(А→В)˄(А→С)
А→(В˅С)=(А→В)˅(А→С)
4.
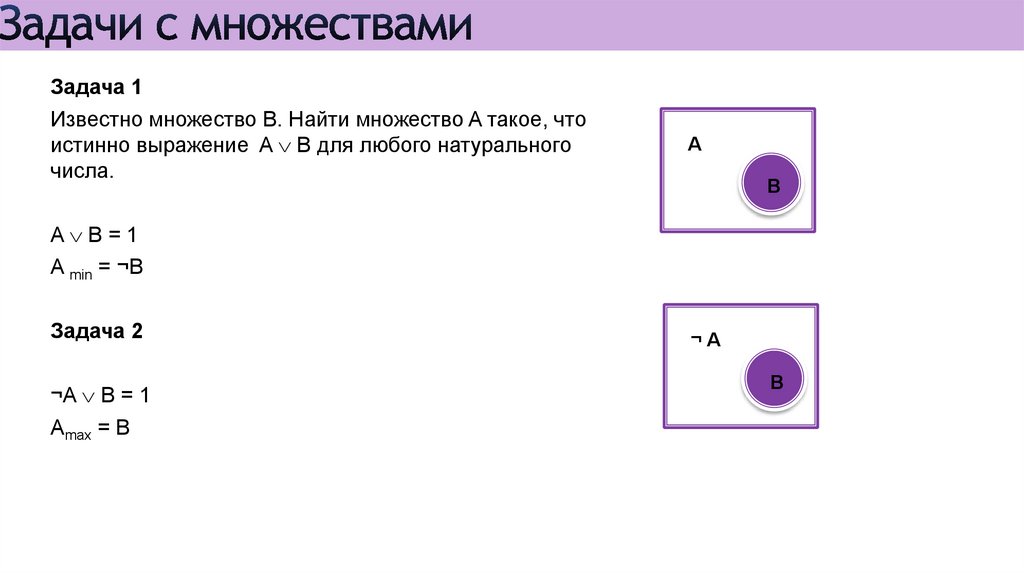
Задача 1Известно множество B. Найти множество A такое, что
истинно выражение A B для любого натурального
числа.
A
B
A B=1
A min = ¬B
Задача 2
¬A B = 1
Amax = B
¬A
B
5.
Для упрощения решений можно пользоваться следующими законами:1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания то используется закон:
где В – известная часть выражения
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием то используется закон:
где В – известная часть выражения
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания то используется закон:
где В – известная часть выражения
Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием то используется закон:
где В – известная часть выражения
6.
Элементами множества А являются натуральные числа.Известно, что выражение
(x {2, 4, 6, 8, 10, 12}) → (((x {3, 6, 9, 12, 15}) /\ ¬(x A)) → ¬(x {2, 4, 6, 8, 10, 12})) истинно (т. е.
принимает значение 1) при любом значении переменной х. Определите наименьшее
возможное значение суммы элементов множества A.
Решение
Обозначим P = {2, 4, 6, 8, 10, 12} Q = {3, 6, 9, 12, 15}
Преобразуем выражение
P → ((Q /\ ¬A) → ¬P) = ¬P \/ (¬(Q /\ ¬A)) \/ ¬P) = ¬P \/ ¬Q \/ A \/ ¬P=
= ¬P \/ ¬Q \/ A = 1
A min = ¬(¬P \/ ¬Q) (см. задача 1)
A min = P /\ Q
Это числа, которые есть и в P, и в Q, а это числа 6 и 12. Их сумма равна 18.
Ответ: 18
7.
Элементами множества А, P и Q являются натуральные числа, причемP = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
Известно, что выражение
((x A) → ¬(x P)) /\ (¬(x Q) → ¬(x A))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов множества A.
Решение
Преобразуем выражение
(A → ¬ P) /\ (¬Q → ¬A) = (¬A \/ ¬P) /\ (Q \/ ¬A) =
= ¬A /\ Q \/ ¬A \/ ¬P /\ Q \/ ¬P /\ ¬A = ¬A /\ (Q \/ 1 \/ ¬P) \/ ¬P /\ Q = ¬A \/ ¬P /\ Q = 1
A max = ¬P /\ Q (см. задача 2)
Это числа, которые есть в Q и нет в P.
A max = {3, 9, 15, 21, 24, 27, 30}
Ответ: 7
8.
Элементами множества А являются натуральные числа. Известно, что выражение(x {2, 4, 6, 8, 10, 12}) → (((x {4, 8, 12, 116}) ¬(x A)) → ¬(x {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее
возможное значение суммы элементов множества A.
Программа на Python:
P = {2, 4, 6, 8, 10, 12} # множество P
Q = {4, 8, 12, 116} # множество Q
A = P & Q # пересечение множеств
print( sum(list(set(A))) )
9.
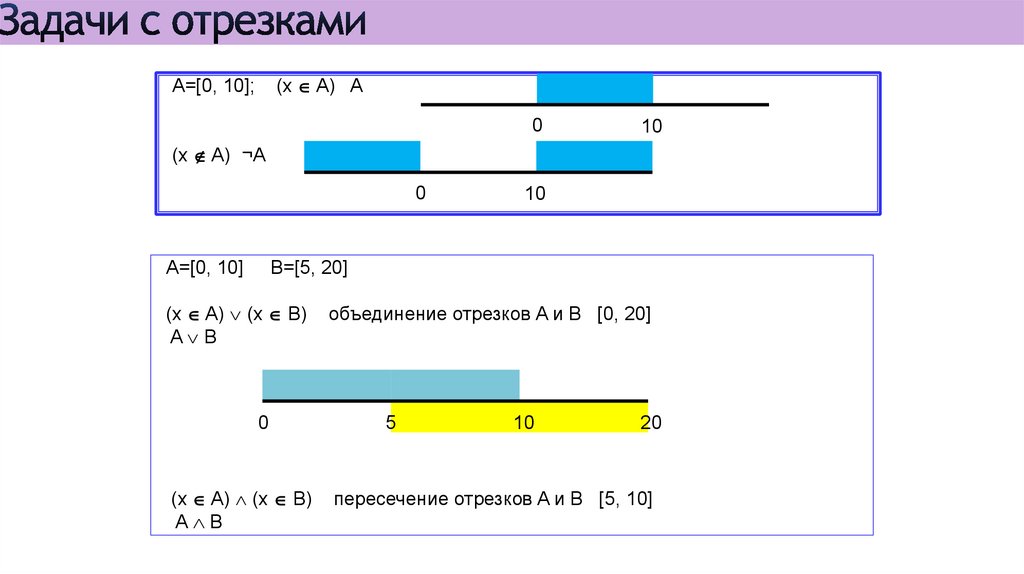
(x A) AA=[0, 10];
0
10
(x A) ¬A
0
A=[0, 10]
10
B=[5, 20]
(x A) (x B)
A B
0
(x A) (x B)
A B
объединение отрезков A и B [0, 20]
5
10
20
пересечение отрезков A и B [5, 10]
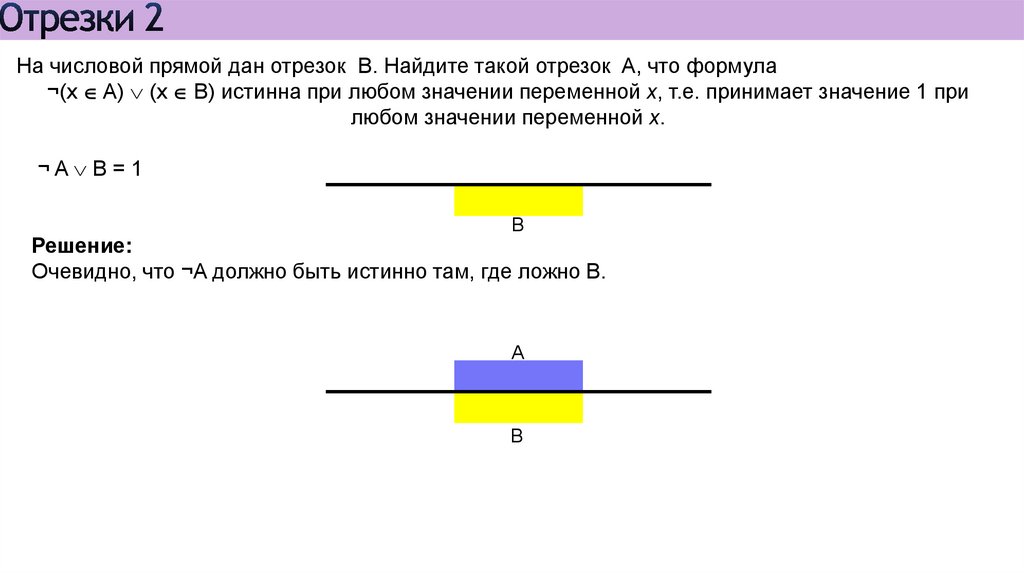
10.
На числовой прямой дан отрезок B. Найдите такой отрезок A, что формула (x A) (x B)истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении
переменной х.
Решение:
A B = 1.
B
Очевидно, что A должно быть истинно там, где ложно B: A min = ¬B
A
B
A
11.
На числовой прямой дан отрезок B. Найдите такой отрезок A, что формула¬(x A) (x B) истинна при любом значении переменной х, т.е. принимает значение 1 при
любом значении переменной х.
¬A B =1
B
Решение:
Очевидно, что ¬A должно быть истинно там, где ложно B.
A
B
12.
На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77].Укажите наименьшую возможную длину такого отрезка A, что формула
(x P) → (((x Q) /\ ¬(x A)) → ¬(x P))
истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении
переменной х.
a b a b
Решение
Преобразуем формулу
a b a b
P → ((Q /\ ¬ A) → ¬P) = ¬P \/ (¬Q \/ A \/ ¬P) = = ¬P \/ ¬Q \/ A \/ ¬P = ¬P \/ ¬Q \/ A
P
37
40
60
77
Q
¬P
¬P
¬P \/ ¬Q \/ A = 1
37
40
60
77
¬Q
A \/ B = 1
B = ¬P \/ ¬Q
Amin = ¬B
(см. задача 1)
Amin = ¬(¬P \/ ¬Q) = P /\ Q
¬Q
P
37
40
60
Q
77
13.
Задание 15 (демо 2022)На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную
длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) /\ ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом
значении переменной х.
17
58
D
29
C
80
(x ∈ D) → ((¬(x ∈ C) /\ ¬(x ∈ A)) → ¬(x ∈ D))=1 Подстановка+преобразуем:
D →(¬C /\ ¬A) →¬D= ¬D\/ (¬C /\ ¬A) →¬D= ¬D \/ ¬ (¬C /\ ¬A) \/ ¬D=
= ¬D \/ С \/ A
Amin = ¬В; B= ¬D \/ С; ¬ B= ¬ (¬D \/ С)=D/\¬С – это отрезок [17;29]
НО В ОТВЕТ НУЖНО НАПИСАТЬ ДЛИНУ: 29-17=12
14.
Задание 15На числовой прямой даны отрезки A = [70; 90], B = [40; 60] и C = [0; N] и
функция F(x)=( (x A) (x B) ( (x C) (x A))
При каком наименьшем числе N функция F(x) истинна более чем для 30 целых
чисел x?
A = {i for i in range(70,91)} # множество A
B = {i for i in range(40,61)} # множество B
C = set() # множество C
for N in range(90):
В цикле будем добавлять элементы в
C.add(N)
множество С, пока сумма элементов А + В*С
if (len(A)+ len(B&C))>30: не достигнет более 30.
print(N)
break










 Информатика
Информатика








