Теория алгоритмов. Трудоемкость вычислений

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость
вычислений»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013

2. КЛАССИЧЕСКАЯ ТЕОРИЯ АЛГОРИТМОВ

В теории алгоритмов задача считается
разрешимой при существовании решающего её
алгоритма. Но для реализации некоторых
алгоритмов может потребоваться больше
времени, чем по современным понятиям
существует вселенная.
Наиболее важные характеристики алгоритма
решения:
1) время;
2) память.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
2

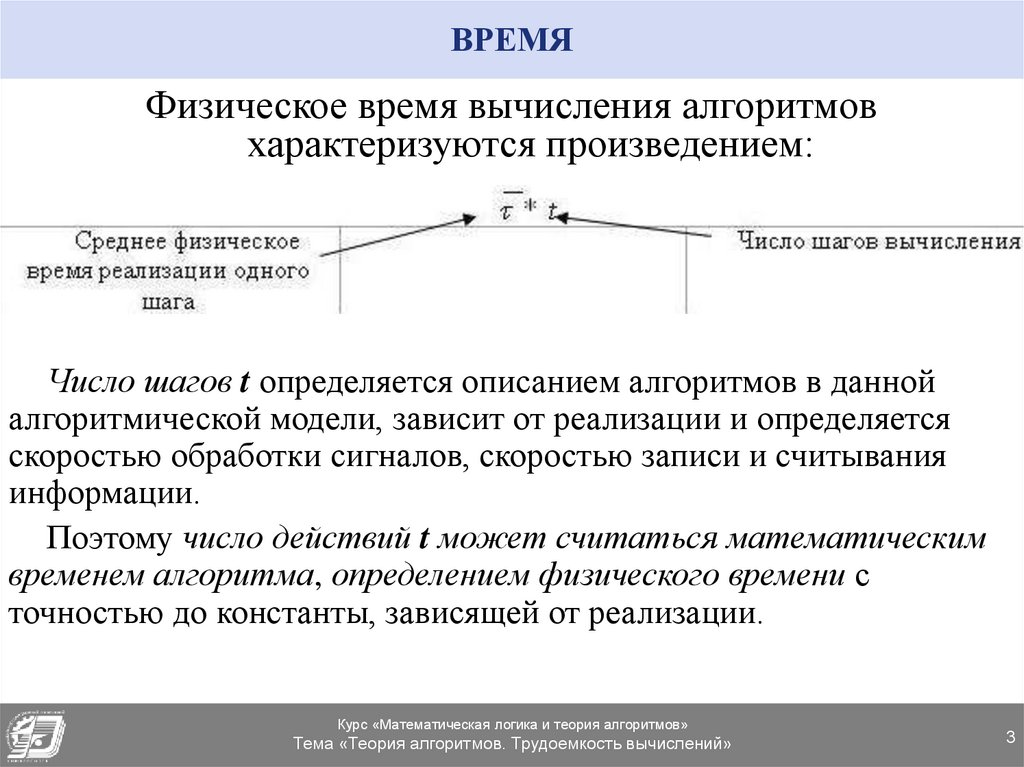
3. ВРЕМЯ

Физическое время вычисления алгоритмов
характеризуются произведением:
Число шагов t определяется описанием алгоритмов в данной
алгоритмической модели, зависит от реализации и определяется
скоростью обработки сигналов, скоростью записи и считывания
информации.
Поэтому число действий t может считаться математическим
временем алгоритма, определением физического времени с
точностью до константы, зависящей от реализации.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
3

4. ПАМЯТЬ

Алгоритм определяется количеством (S) единиц
памяти: S ≤ Mt,
где М - это максимальное число единиц памяти
используемых в данной машине на одном шаге,
t – число шагов вычислений.
t может существенно превосходить S, например,
возможно соотношение t ≥ Sc.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
4

5. ХАРАКТЕРИСТИКИ АЛГОРИТМА

Трудоёмкость алгоритма – это число элементов
действий, выполненных во время его вычислений.
Полной характеристикой конкретного варианта
задачи является его формальное описание.
Характеристикой сложности можно считать его
объём, который иногда называется размерностью
задачи.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
5

6. ТРУДОЕМКОСТЬ

Трудоёмкость задачи относительно машины М это минимум из трудоёмкостей алгоритмов, решающих
эту задачу, на конкретной машине М.
Трудоёмкость оценивают сверху, т.е. указывают
конкретный алгоритм, трудоёмкость которого меньше
других алгоритмов, решающих эту задачу.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
6

7. ТРУДОЕМКОСТЬ

Скорость вычислений на разных машинах различна, строить
трудоёмкость вычислений, привязываясь к некоторым
конкретным моделям, неудобно:
• ни для теории (такая привязка не даёт достаточно
объективных характеристик трудоёмкости задачи, т.е. не
позволяет отделить влияние особенности выбранной модели от
специфики самой задачи);
• ни для практики (разнообразие реальных машин растёт и
нужны общие понятия и методы оценки трудоёмкости решения
задачи, которые сохраняют свою силу при любых изменениях в
мире компьютеров).
Поэтому теория трудоёмкости модели инвариантна, и
вопрос не в том возможна ли она, а в том, как её построить.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
7

8. КЛАССЫ ТРУДОЕМКОСТИ ЗАДАЧ

Задача принадлежит классу P, если
существует машина Тьюринга, на которой она
решается с
трудоёмкостью, полиномиально зависящей от
параметров её размерности, т.е. трудоёмкости, не
превосходящей CoMC1n1C2n2C3,
где Со, С1, С2, С3 – const (свои для каждой
задачи).
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
8

9. ЭФФЕКТИВНОСТЬ АЛГОРИТМА

O(Nk)
–
время
работы
алгоритма,
при
наличии N входных данных(это число, названное
размерностью задачи), состоящее не более O(Nk) – где
k-const, не зависящая от N.
Задачи класса P могут считаться характерно
решаемыми при условии, что показатели степени С1,
С2, С3 не слишком велики O(Nk), k - не зависит от N.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
9

10. КЛАСС P 

КЛАСС P
• Следующие
натуральные
числа ( X + 1 ).
• Суммы Y= X1 + X2
• Произведения Y= X1 * X2
• Задача P E R T
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
10

11. КЛАСС РС

РС – класс задач с полиноминальной трудоемкостью
проверки.
Задача
принадлежит
классу
PC,
если
её
предикат Pm,n1,n2(¬X, ¬Y) (или Pm(¬X,¬Y)) вычисляется на
некоторых МТ с полиномиальной трудоёмкостью.
Трудоёмкость задачи о корнях, о покрытии множеств
подмножествами, о выполнимости КНФ, об определении
значений двоичных переменных Y1,Y2,...Ym
удовлетворяет
условиям:
n
≤
∑ Xji Yj ≥ Mi (i = 1, 2, .., l)
j=1
=
Это класс PC.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
11

12. КЛАСС NP. РЕШЕНИЕ ЗАДАЧ

КЛАСС NP. РЕШЕНИЕ ЗАДАЧ
Чтобы решить данную массовую задачу перебора
при значении X параметров размерностей m, n1, n2 или
только m, каждому варианту x(x1, x2, .., xm) такой задачи
надо
уметь
поставить
в
соответствии
ответ ¬y(y0,y1,.., ym).
Если y0=1, то вариант имеет решение и
значение y1, y2, ..,ym – это описание некоторого из них
(решение может быть не единственным).
Если y0=0, то задача не имеет решения, и
значение y1, y2, .., ym может быть каким угодно.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
12

13. КЛАСС NP

Пусть имеется недетерминированная машина
Тьюринга
NT,
которая
при
любом
варианте ¬x данной машинной задачи не
позднее, чем через C0mc1 шагов, остановится и
даст ответ:
• положительный (y0=1),
• отрицательный (y0=0),
причём C0 и C1 – const.
Тогда рассматриваемая задача принадлежит
классу NP.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
13

14. КЛАСС NP

Обычная машина Тьюрингаэто
частный случай недетерминированной
машины
с
количеством
разветвлений k=1
все задачи класса P- это задачи
класса NP.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
14

15. КЛАСС NP. ВЫВОДЫ

1. Искомый
инвариант
теории
трудоёмкости
вычисленийпонимание полиномиальности трудоёмкости →
если задача имеет полиномиальную трудоёмкость
вычисления, то это её свойство не зависит от выбора
машины.
Напротив, значение степени в оценке трудоёмкости
при смене машины может изменится, и более тонкие
характеристики трудоёмкости могут не быть
инвариантными.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
15

16. КЛАСС NP. ВЫВОДЫ

2. Понятие полиномиальности трудоёмкос
ти проверки и связанный с ним
класс PC:
Верно, что P ≠ PC → существует
обширный класс задач, для которых
проверить правильность предъявленного
ответа существенно проще, чем найти
ответ.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
16

17. КЛАСС NP. ВЫВОДЫ

3. Понимание NP – полноты - выделяет обширный
класс задач, который в инвариантных терминах
эквивалентен трудоёмкости и является самым
трудоёмким среди задач классов PC и NP. Можно
доказать, что либо P=PC=NP, либо P PC
NP.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
17

18. УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА(МТ)

МТ состоит из:
1. Управляющего устройства (может находиться в
одном из состояний, образующих конечное множество
Q = {q1 , … , qn } );
2. Ленты, разбитой на ячейки (может быть записан
один из символов конечного алфавита А = { а1, … ,
am} );
3. Устройства обращения к ленте (считывающая,
пишущая головка).
Среди состояний МТ выделены:
• начальное ( q1) – на начальном этапе работы;
• конечное ( qz) – машина останавливается.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
18

19. ПАМЯТЬ МТ

Память МТ – конечное множество
состояний(внутренняя память) и лента.
Лента бесконечна в обе стороны, однако в
начальный момент времени только конечное
количество ячеек ленты заполнено непустыми
символами(в любой последующий момент лишь
конечный отрезок ленты будет заполнен
символами).
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
19

20. УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА

Поставим задачу построения МТ реализации алгоритма
воспроизведения. Для МТ вычислительной функции от одной
переменной формулировка этой задачи такова:
построить МТ скорость вычисления функции от двух
переменных и такую, что для любой МТ с с/с команд ∑т.
Любую машину Тьюринга V, обладающую следующими
свойствами, называют универсальной машиной Тьюринга:
1. V(∑т, L) = T(α), если T(α) определена (т.е. МТ останется
при исходных данных α),
2. V(∑т, L) не останавливается, если T(α) не определена.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
20

21. УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА

Существование универсальной машины Тьюринга
означает, что систему команд ∑т любой машины
Тьюринга можно интерпретировать двояким образом:
• как описание работы конкретного устройства МТ;
• как программу для универсальной машины V.
Для инженера, это обстоятельство вполне
естественно: любой алгоритм может реализоваться:
1) аппаратно;
2) программно.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
21

22. ТЕЗИС ТЬЮРИНГА

Всякий алгоритм может быть реализован машиной Тьюринга.
Доказать его нельзя, т.к. само понятие алгоритма является
неточным. Это не теорема и не постулат математической теории,
а утверждение, которое связывается теорию, с теми объектами,
для описания которых она создана. По своему характеру тезис
Тьюринга напоминает гипотезы физики, об адекватности
математических моделей физическим явлением и процессам.
Подтверждением тезиса является:
1. Математическая практика
2. Описание алгоритмов термина другой алгоритмической
модели может быть сведено к его описанию в виде машины
Тьюринга.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
22

23. ПРОБЛЕМА ОСТАНОВКИ

Результативность – требование, определяющее,
приведет ли работа алгоритма при исходных данных а к
результату или нет.
Иначе говоря, нужно построить алгоритм B
(задача1) такой, что:
B(A, α) = Истина, если A(α) даёт результат;
B(A, α) = Ложь, если А(α) не даёт результата.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
23

24. ПРОБЛЕМА ОСТАНОВКИ

В силу тезиса Тьюринга задачу 1 можно
сформулировать, как задачу о построении МТ:
построить машину Т0 такую, что для любой МТ и
любых исходных α для Т :
Т0 (∑т, α) = Истина, если машина Тьюринга (α)
остановится,
Т0 (∑т, α) = Ложь, если машина Т(α) не
остановится.
Это проблема остановки очень напоминает задачу
о построении универсальной машины.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
24

25. ТЕЗИС ТЬЮРИНГА

Теорема:
Не существует машины Тьюринга Т0,
решающей проблему остановки для
производства машины Тьюринга.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
25

26. ПРОБЛЕМА ОСТАНОВКИ

В силу тезиса Тьюринга невозможность построения
машины Тьюринга означает отсутствие алгоритма
решения данной проблемы
полученная
теория
даёт
первый
пример
алгоритмической неразрешимой проблемы – проблемы
остановки для МТ.
Проблема остановки для МТ - это проблема
определения результативности алгоритма. То есть
отсутствует единый алгоритм, решающий данную
проблему, но не исключается возможность решения
проблемы в частных случаях различными средствами.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
26

27. ПРОБЛЕМА ОСТАНОВКИ

Для отдельных классов
остановки может быть решена
МТ
проблема
неразрешимость общей проблемы остановки
вовсе не снимает необходимость доказывать
сходность алгоритмов, а лишь показывает, что
поиск таких доказательств нельзя полностью
автоматизировать.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
27

28. ПРОБЛЕМА ОСТАНОВКИ. ВЫВОДЫ

Неразрешимость проблемы остановки машины
нет общего алгоритма для отладки программалгоритма, который по тексту любой программы и ее
данным определял бы, зациклится ли программа на
этих данных или нет.
Но большинство программ удаётся отладить:
установить наличие зацикливания;
-найти его причину;
-устранить с помощью опыта и искусства
программиста.
Курс «Математическая логика и теория алгоритмов»
Тема «Теория алгоритмов. Трудоемкость вычислений»
28

29.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013