Похожие презентации:
Координаты в математике и географии
1.
Координаты вматематике и географии
2.
Цель:выяснить применение системы
координат в математике и
географии
3.
Задачи:1. Познакомиться с историей
возникновения системы координат.
2. Научиться свободно ориентироваться на
координатной плоскости и на географической
карте
3.Научиться «рисовать» в прямоугольной
системе координат.
4.
Историческая справка.Во II – III веках до н. э. меридианы и параллели впервые
появились на карте Эратосфена. Однако, они еще не
представляли собой координатной сетки.
5.
Во II в. до н. э. Гиппарх впервые разделил круг на 360 частей ипредложил опоясать на карте Земной шар меридианами и
параллелями. Ввел понятие – экватор, провел параллели и через
полюса провел меридианы. Таким образом, была создана
картографическая сеть и стало возможным наносить на карту
географические объекты.
6.
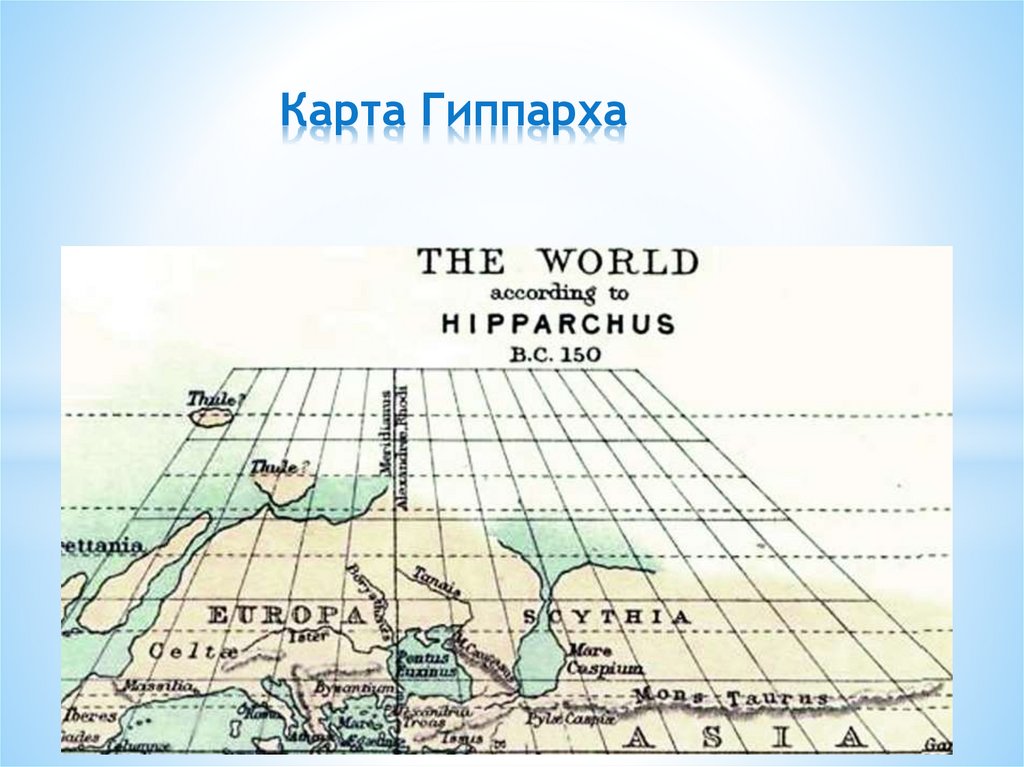
Карта Гиппарха7.
Географическая широта –это величина дуги
меридиана от экватора до
заданной точки.
Из курса геометрии
известно, что дуги
измеряются как в линейных
величинах, так и в угловых:
градусах и радианах
Географическая долгота – это
величина дуги параллели от
нулевого меридиана до заданной
точки.
Видно, что географические
координаты – понятие
математическое.
8.
В XIV в. французский математик Никола Орезм предложилввести , по аналогии с географическими, координаты на
плоскости. Он предложил покрыть плоскость прямоугольной
сеткой и называть широтой и долготой то, что мы теперь
называем абсциссой и ординатой. Это положило начало
созданию метода координат и связало алгебру и геометрию.
9.
Рене Декарт (1596-1650) – французскийматематик, философ, физик и физиолог
В математике именно
ему принадлежит
основная заслуга в
создании метода
координат, который
был положен в основу
аналитической
геометрии
10.
Чтобы найти своеместо в зале,
сначала мы ищем
свой ряд, затем своё
место
Чтобы найти свое
место в зале,
сначала мы ищем
свой ряд, затем своё
место
11.
Немалой заслугой Декарта было введение удобныхобозначений, используемых сегодня: x, y, z – для
неизвестных , a, b, с - для коэффициентов, а также
обозначение степеней.
В настоящее время декартовы координаты
представляют собой ортогональные оси с одинаковым
масштабом по всем направлениям, точка О является
началом координат.
12.
География «geo» – Земля, «grafo» – пишу.Геометрия «geo» – земля, «metreo» измерять.
Эти две науки были тесно связаны между
собой, их возникновение обусловлено
практической деятельностью людей того
времени.
13.
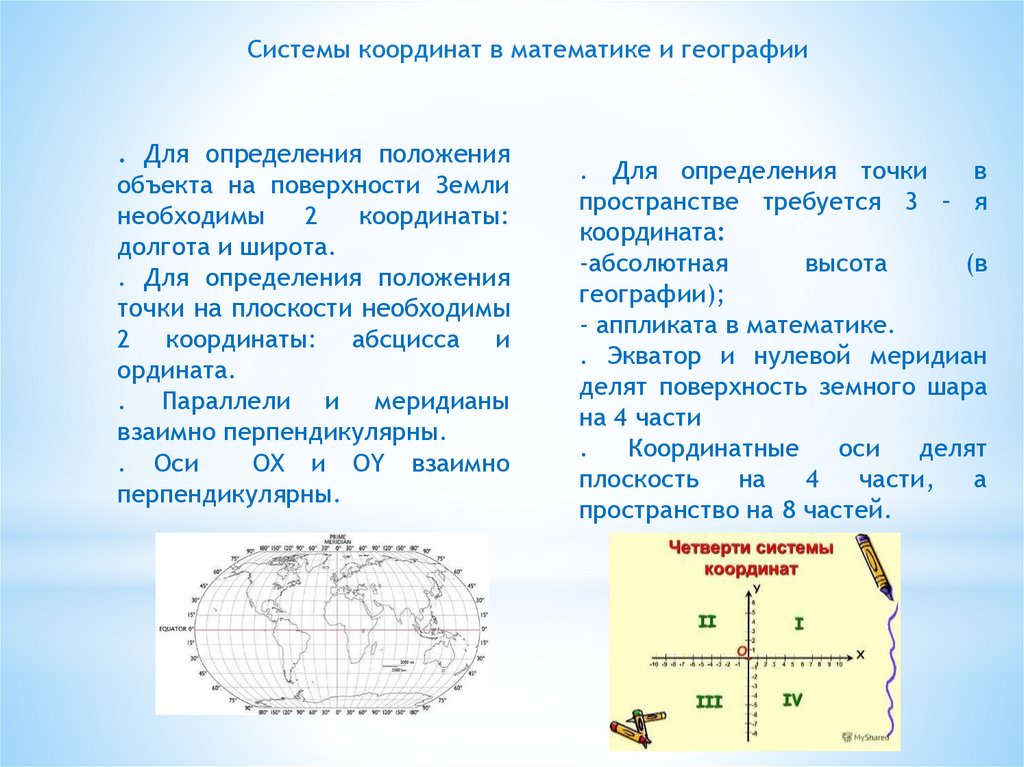
Системы координат в математике и географии. Для определения положения
объекта на поверхности Земли
необходимы
2
координаты:
долгота и широта.
. Для определения положения
точки на плоскости необходимы
2 координаты: абсцисса и
ордината.
. Параллели и меридианы
взаимно перпендикулярны.
. Оси
OX и OY взаимно
перпендикулярны.
. Для определения точки
в
пространстве требуется 3 – я
координата:
-абсолютная
высота
(в
географии);
- аппликата в математике.
. Экватор и нулевой меридиан
делят поверхность земного шара
на 4 части
.
Координатные
оси
делят
плоскость
на
4
части,
а
пространство на 8 частей.
14.
1. Слова «геометрия» и «география» имеют древнегреческое происхождениеи связаны с практической деятельностью людей на поверхности Земли.
2. Географические широта и долгота измеряются в градусах, так как
представляют собой дуги окружностей, стягивающих центральные углы, т. е.
являются математическими величинами.
3. И в математике, и в географии используются как прямоугольные, так и
полярные координаты.
4. В прямоугольных системах координат оси (экватор и нулевой меридиан,
оси OX и OY) взаимно перпендикулярны и делят плоскость на 4 части:
Северное, Южное, Западное и Восточное полушария в географии и I, II, III, IV
квадранты.
5. Положение точки на плоскости задается 2 координатами: широтой и
долготой в географии, абсциссой и ординатой в математике.
6. При определении положения объекта в пространстве появляется третья
координата: абсолютная высота в географии и аппликата в математике.
15.
Создание «рисунков» в прямоугольнойсистеме координат.













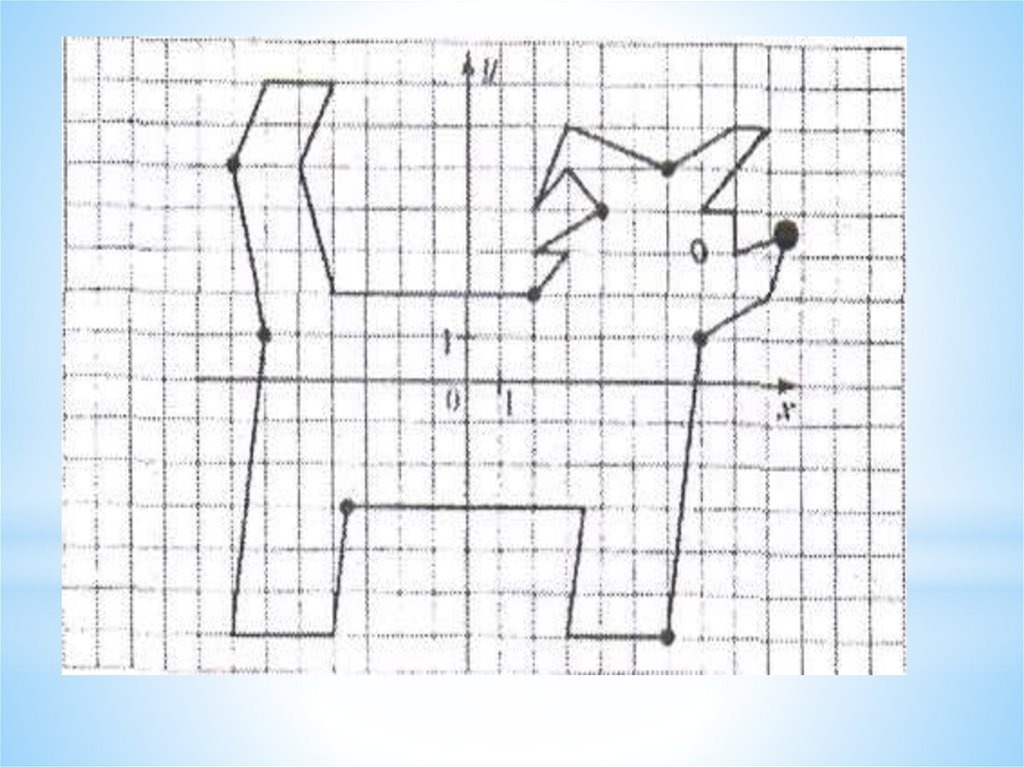

 Математика
Математика