Реляционная алгебра

1.

1

2. Алгебра -

Алгебра • множество объектов с заданной на нем
совокупностью операций, замкнутых
относительно этого множества,
называемого основным множеством.
• Основным множеством в реляционной
алгебре является множество отношений.
2

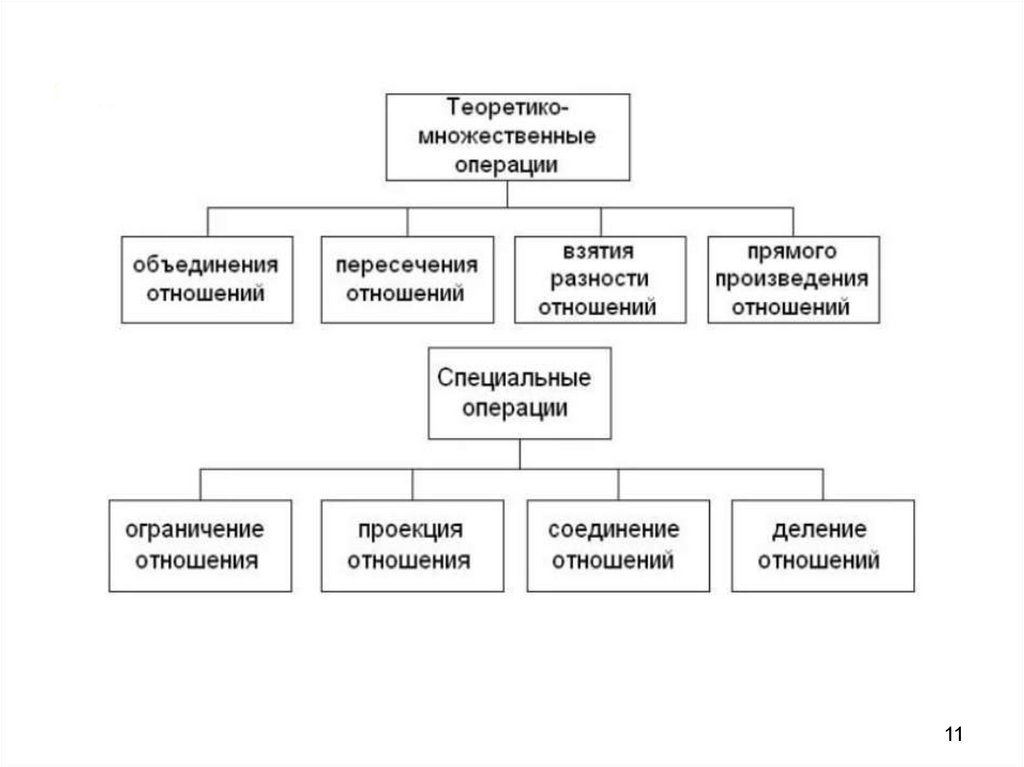
3. Основная идея реляционной алгебры

Поскольку отношения являются
множествами, средства манипулирования
отношениями могут базироваться на
традиционных теоретико-множественных
операциях, дополненных специальными
операциями, специфичными для
реляционных баз данных.
3

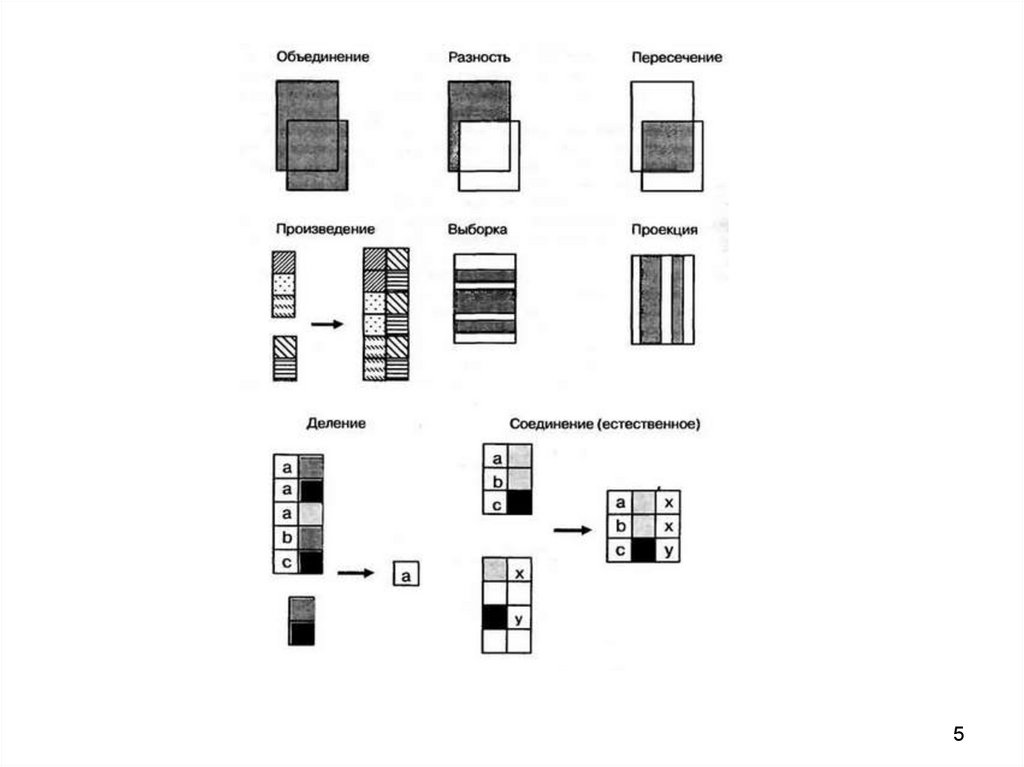
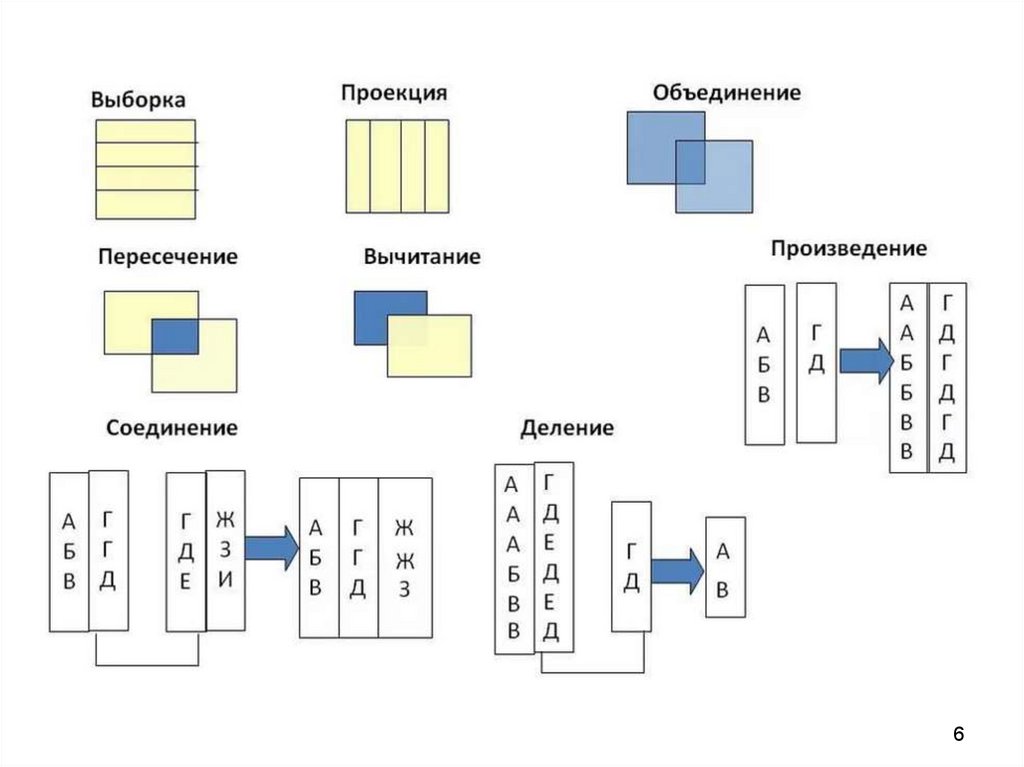
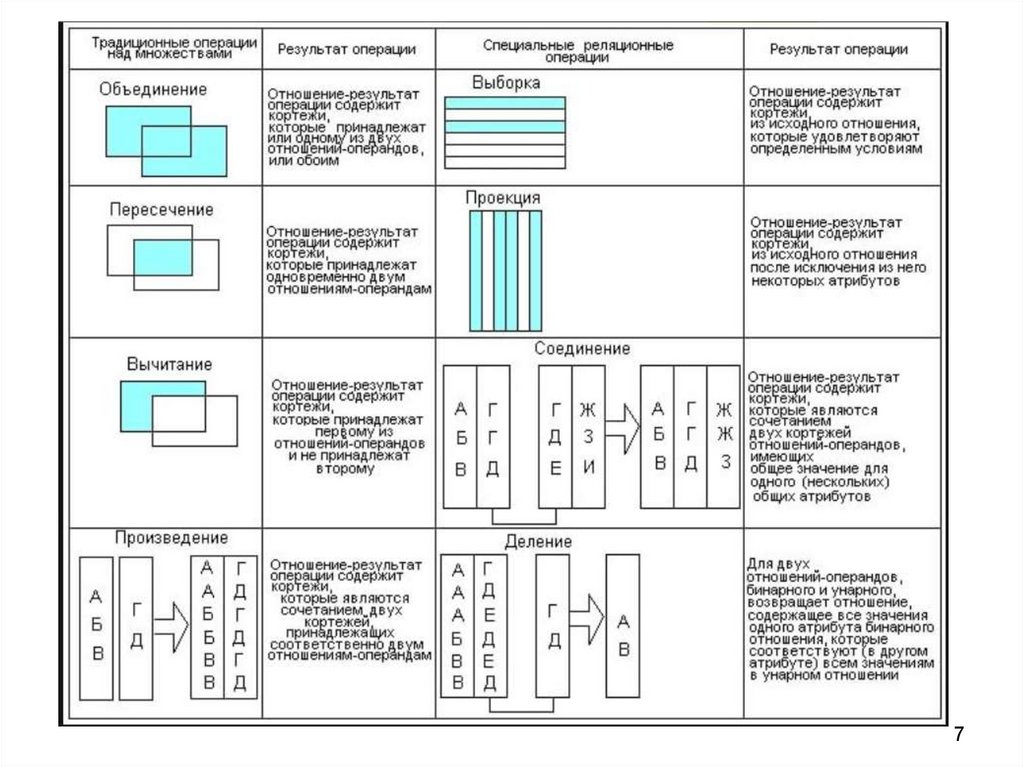
4. Операции над отношениями

• Операции над множествами: объединение,
пересечение, разность, деление, декартово
произведение
• Специальные операции: проекция,
соединение, выбор
4

5.

5

6.

6

7.

7

8. 2 группы языков

• На основе реляционной алгебры процедурный, операнды и результаты
являются отношениями;
• На основе реляционного исчисления –
непроцедурный, описательный, запрос к БД
содержит информацию о желаемом
результате, для записи запросов
определены правила.
8

9. Операции Кодда

• Объединение
• Разность (вычитание)
• Пересечение
• Произведение
• Выборка (селекция, ограничение,
фильтрация, горизонтальный выбор)
• Проекция (вертикальный выбор)
• Деление
• Соединение (сцепление, конкатенация)
9

10. Совместимость структур

• При выполнении бинарной операции
участвующие в операциях отношения
должны быть совместимы по структуре
• Совместимость структур отношений
означает совместимость имен атрибутов и
типов соответствующих доменов
10

11.

11

12. Базовые теоретико-множественные операции

• Объединение
• Разность (вычитание)
• Пересечение
• Произведение
12

13. Объединение

Объединением двух совместимых
отношений R1 и R2 одинаковой
размерности (R1 UNION R2) является
отношение R, содержащее все элементы
исходных отношений за исключением
повторений
13

14. Вычитание

Вычитание двух совместимых отношений
R1 и R2 одинаковой размерности (R1
MINUS R2) есть отношение R, состоящее
из множества кортежей, принадлежащих
R1, но не принадлежащих R2
14

15. Пересечение

Пересечение двух совместимых
отношений R1 и R2 одинаковой
размерности (R1 INTERSECT R2) порождает
отношение R, содержащее кортежи,
одновременно принадлежащие обоим
подмножествам
15

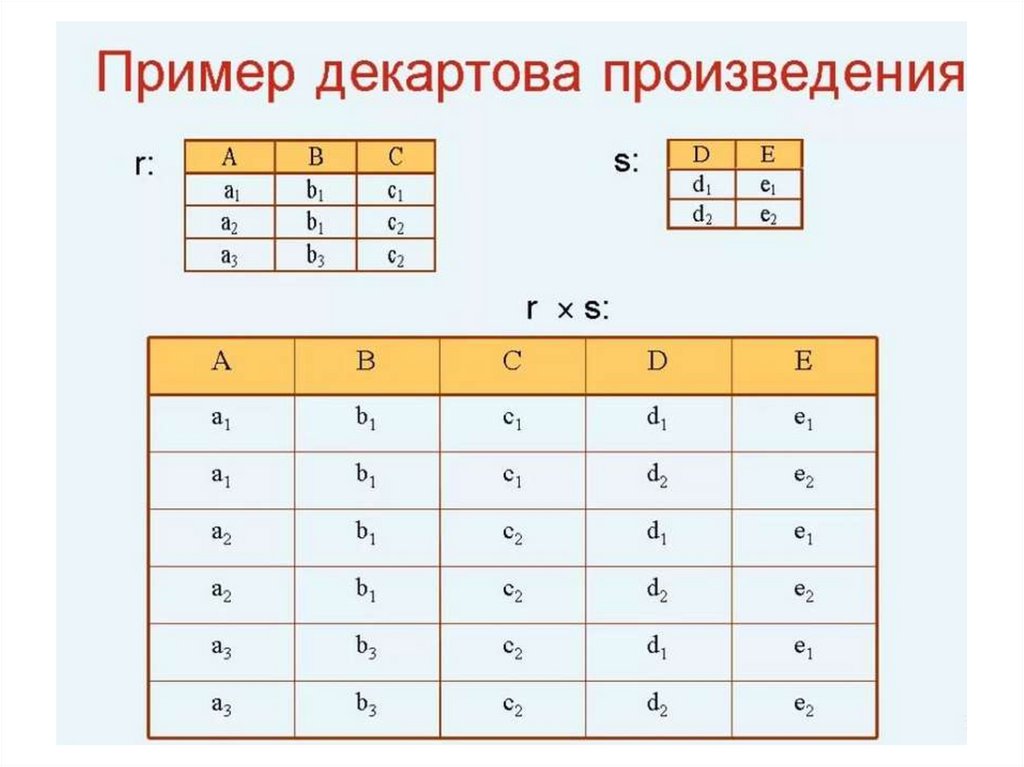
16. Произведение

Произведение отношения R1 степени k1 и
отношения R2 степени k2 (R1 TIMES R2),
которые не имеют одинаковых имен атрибутов,
есть такое отношение R степени (k1 + k2),
заголовок которого представляет собой
сцепление заголовков отношений R1 и R2, а
тело имеет кортежи такие, что первые k1
элементов кортежей принадлежат множеству
R1, а последние k2 элементов – множеству R2.
16

17.

17

18. Специальные реляционные операции

• Выборка (селекция, ограничение,
фильтрация, горизонтальный
выбор)
• Проекция (операция вертикального
выбора)
• Деление
• Соединение (сцепление,
конкатенация)
18

19. Выборка

Выборка (R WHERE f) представляет собой
новое отношение с тем же заголовком и
телом, состоящим из таких кортежей
отношения R, которые удовлетворяют
истинности логического выражения,
заданного формулой f.
19

20.

20

21. Проекция

Проекция отношения А на атрибуты X,Y,…,Z
(A[X,Y,…,Z]), где множество {X,Y,…,Z} является
подмножеством полного списка атрибутов
заголовка отношения А, представляет
собой отношение с заголовком X,Y,…,Z и
телом, содержащим кортежи отношения А,
за исключением повторяющихся кортежей
21

22. Проекция

Дополнительные варианты записей:
• Отсутствие списка атрибутов подразумевает
указание всех атрибутов (тождественная
проекция).
• R[] – пустая проекция, результат – пустое
множество.
• Операция проекции может применяться к
произвольному отношению, в т.ч. и к
результату выборки.
22

23. Деление

Результатом деления отношения R1 с атрибутами
А и В на отношение R2 с атрибутом В (R1
DIVIDEBY R2) , где А и В простые или составные
атрибуты, причем В – атрибут общий,
определенный на одном и том же домене,
является отношение R с заголовком А и телом,
состоящим из кортежей r таких, что в отношении
R1 имеются кортежи (r,s), причем множество
значений s включает множество значений
атрибута В отношения R2.
23

24. Соединение

• Общая операция соединения
• Θ – соединение (тета)
• Эквисоединение
• Естественное соединение
• Внешнее соединение
24

25. Соединение

Соединение C(R1,R2) отношений R1 и R2
по условию, заданному формулой f
представляет собой отношение R, которое
можно получить путем декартова
произведения отношений R1 и R2 с
последующим применением к результату
операции выборки по формуле f (R1 TIMES
R2) WHERE f.
25

26. Θ – соединение

• Формула f имеет произвольный вид
• (R1 TIMES R2) WHERE A знак B
• JOIN
26

27. Эквисоединение

F задает равенство операндов, т.е.
возвращаются только те записи, для
которых значения указанных полей
совпадают.
27

28. Естественное соединение

• Частный случай эквисоединения
• Основано на операторе равенства
• Участвуют все общие поля
• В результирующий набор записей
включен только один набор общих
полей
• Обладает свойством ассоциативности
28

29. Внешнее соединение

• OUTER JOINS
• Возвращает все записи, участвующие в
соединении, которые возвращает
внутреннее соединение плюс все записи из
одного или обоих наборов данных,
участвующих в соединении
29

30. Внешнее соединение

• Левое (один из «один ко многим»)
• Правое (все из «многих к одному»)
• Полное (все записи)
30

31. Операции Дейта

• Переименование (имя атрибута)
• Расширение (добавление нового атрибута)
• Подведение итогов (вертикальные вычисления)
• Присвоение (замена предыдущего значения
отношения на новое)
• Вставка
• Обновление
• Удаление
• Реляционное сравнение
31

32. Переименование

• RENAME <исх_отношение>
<старое_имя_атрибута> AS
<новое_имя_атрибута>
• RENAME S Город_П AS Город_размещ
32

33. Расширение

• EXTEND <исх_отношение> ADD
<выражение> AS <новый_атрибут>
• EXTEND (JOIN SP) ADD (Вес*Кол-во) AS
Общий_вес
33

34. Подведение итогов

• SUMMARIZE <исх_отн> BY (<список
атрибутов>) ADD <выражение> AS <новый
атрибут>
• SUMMARIZE SP BY (П#) ADD COUNT AS
Количество_поставок
34

35. Присвоение

Выражение_цель ::= Выражение_источник
S::= S UNION {{<П#:’S6’>, <Имя:’Борис’>,
<Статус:’50’>,<Город_П:’Мадрид’>}}
35

36. Вставка

INSERT <Выражение_источник> INTO
<Выражение_цель>
INSERT (S WHERE Город_П=‘Москва’) INTO
Temp
36

37. Обновление

UPDATE <Выражение_цель>
<список_элементов>
UPDATE P WHERE Тип=‘каленый’
Город_Д=‘Минск’
37

38. Удаление

• DELETE S <выражение_цель>
• DELETE S Where Статус<20
38

39. Реляционное сравнение

Выражение_1 знак Выражение_2
S[Город_П] = P[Город_Д]
= равно
<> не равно
<= собственное подмножество
< подмножество
>= собственное надмножество
> надмножество
39

40. Правила записи выражений

• Необходимо учитывать приоритет
операций, который должен быть определен
• Существуют тождественные
преобразования, позволяющие записать
одно и то же выражение по-разному
• Нужно обеспечивать совместимость
участвующих в выражении отношений
40

41. Реляционное исчисление

Для получения результата необходимо
указать свойства искомого отношения без
конкретизации его получения
41

42. Запрос

Получить номера и города поставщиков,
выпускающих деталь Р2
42

43. Реляционная алгебра

• Образовать естественное соединение
отношений S и SP по атрибуту П#
• Выбрать из результата этого соединения
кортежи с деталью Р2
• Спроецировать результат предыдущей
операции на атрибуты П# и Город_П
43

44. Реляционное исчисление

• Получить атрибуты П# и Город_П для таких
поставщиков, для которых существует
поставка в отношении SP с тем же
значением атрибута П# и со значением Р2
атрибута Д#
44

45. Варианты исчислений

• Исчисление кортежей
• Исчисление доменов
45

46. Исчисление кортежей

• RANGE of <переменная> IS <список>
• Примеры
• - RANGE of SX IS S;
• - RANGE of SPX IS SP;
• - RANGE of SY IS (SX) Where
SX.Город_П=‘Москва’, (SX) Where EXISTS SP
(SPX.П#=SX.П# AND SPX.Д#=‘P2’);
46

47. Форма Бэкуса-Наура

• <выражение>::=(А,[b,[…z]…]) [Where RF]
• A ::= {<переменная>|<переменная>.
<атрибут>}[AS <атрибут>]
• RF ::= условие| NOT RF |
условие AND RF | условие OR RF |
IF условие Then RF |
EXISTS переменная (RF) |
FORALL переменная (RF)
47

48. Получить имена поставщиков, которые поставляют все детали

• SX.Город_П WHERE FORALL PX (EXISTS SPX
(SPX.П#=SX.П# and
SPX.Д#=SX.Д# ))
• SX.Город_П WHERE NOT EXIST PX (NOT EXISTS
SPX (SPX.П#=SX.П# and
SPX.Д#=SX.Д# ))
48

49. Исчисление доменов

• Дополнительная форма условия – условие
принадлежности
• Лакроикс и Пироттс
• Примеры:
• (SX) WHERE S (П#: SX)
• (SX) WHERE S (П#: SX, Город_П:’Москва’)
• NAMEX WHERE EXISTS SX (S(П#:SX, Имя:
NAMEX) AND FORALL PX (IF P(Д#:PX) THEN
(SP (П#:SX,Д#:PX)))
49