Представление объёма интегралом. Два доказательства теоремы

1.

2. Представление объёма интегралом

Два доказательства
теоремы

3.

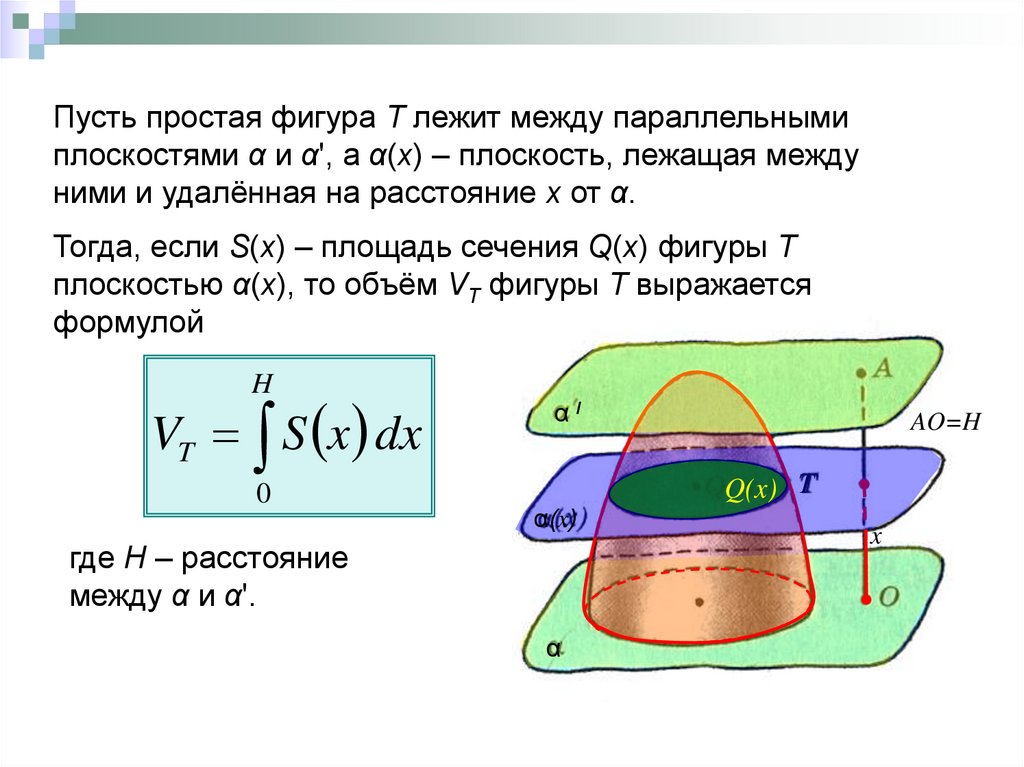
Пусть простая фигура Т лежит между параллельными
плоскостями α и α', а α(х) – плоскость, лежащая между
ними и удалённая на расстояние х от α.
Тогда, если S(х) – площадь сечения Q(x) фигуры Т
плоскостью α(х), то объём VT фигуры Т выражается
формулой
H
VT S x dx
0
α/
AO=H
Q(x) T
α(x)
где Н – расстояние
между α и α'.
α
x

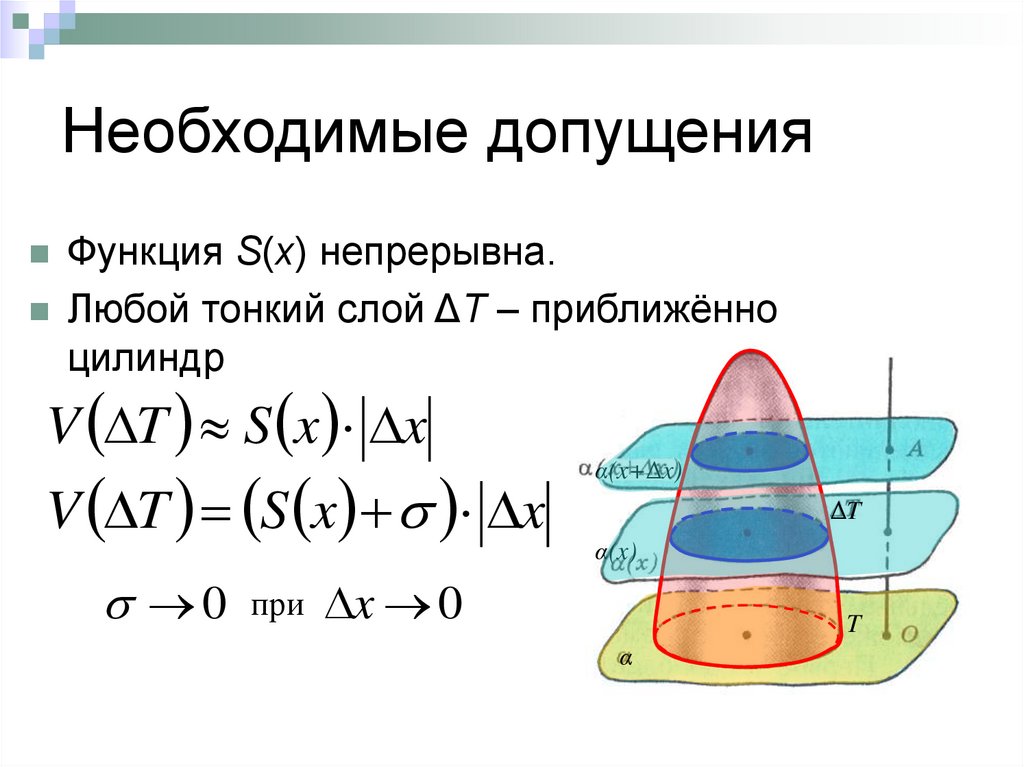
4. Необходимые допущения

Функция S(х) непрерывна.
Любой тонкий слой ΔТ – приближённо
цилиндр
V T S x x
V T S x x
0
при
α(x+Δx)
ΔT
α(x)
x 0
T
α

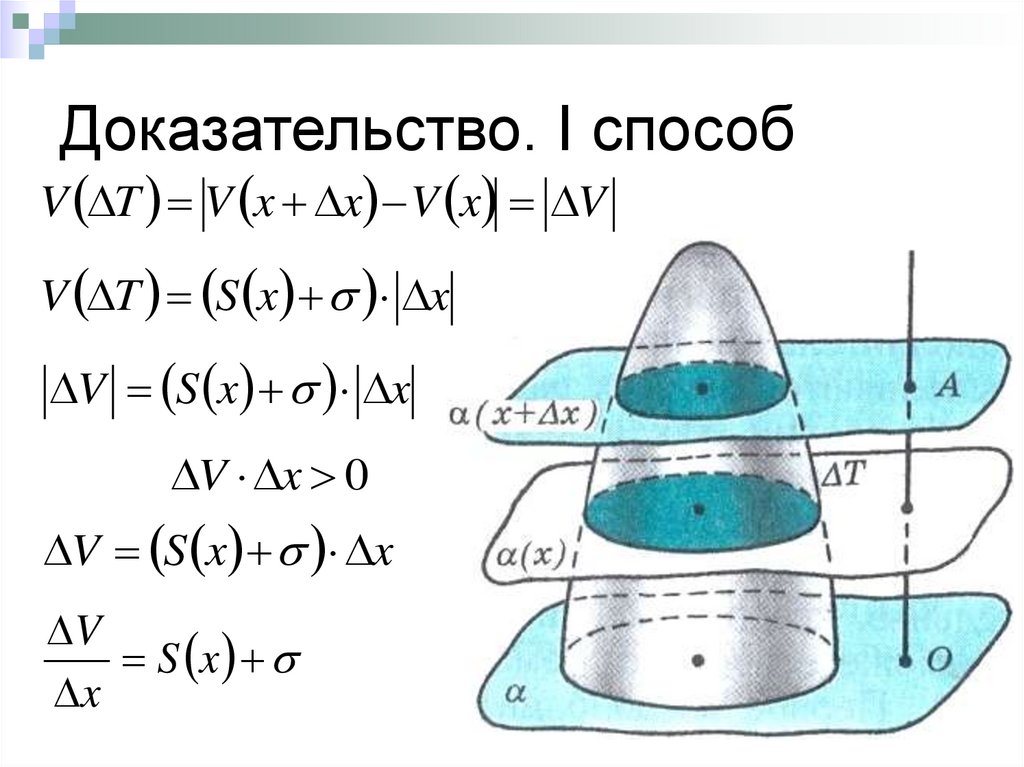
5. Доказательство. I способ

V T V x x V x V
V T S x x
V S x x
V x 0
V S x x
V
S x
x

6. Доказательство. I способ

V V x x V x
V
S x
x
0 при x 0
V
lim
S x
x 0 x
V
lim
V x S x
x 0 x

7. Доказательство. I способ

V x S x
V(x) – первообразная S(x)
V 0 0
V H VT
H
VT V H V 0 S x dx
0

8. Доказательство. II способ

x 0; H
0
0
x C , C : C T C
S S

9. Доказательство. II способ

C T C
VC V T VC
VC S x
VC S x
S x V S x

10. Доказательство. II способ

S x V S x
V x 0
V
S
S
x
S S x S
S S
V
S x
x
V
lim
S x
x 0 x

11. Доказательство. II способ

V x S x
V(x) – первообразная S(x)
V 0 0
V H VT
H
VT V H V 0 S x dx
0