Похожие презентации:
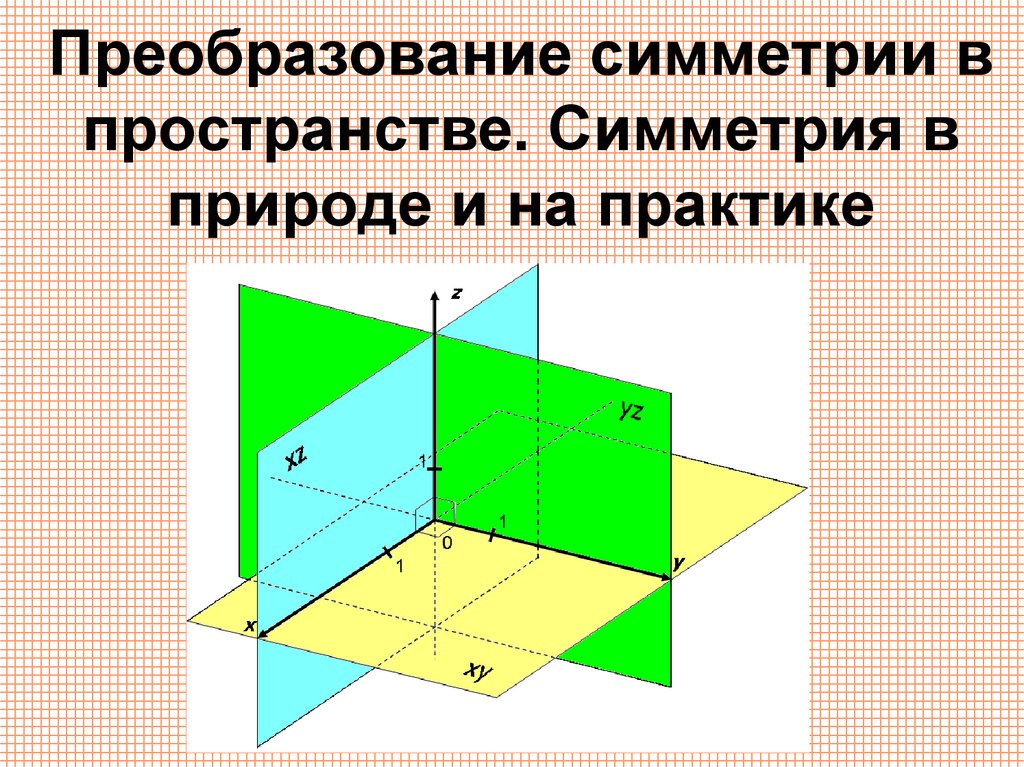
Преобразование симметрии в пространстве. Симметрия в природе и на практике
1. Преобразование симметрии в пространстве. Симметрия в природе и на практике
2. Преобразование симметрии в пространстве. Симметрия в природе и на практике
3.
Центральнаясимметрия
Построим точку A0,
симметричную данной
точке относительно
точки O.
z
c
Пусть A(a; b; c)
A
1
−a
−b
a
x
0
1
1
b
y
A0
−c
Тогда координаты точки A0(−a; −b; −c).
4.
Осеваясимметрия
z
c
Пусть A(a; b; c)
A
Построим точку A1,
симметричную
данной точке
относительно оси Ox.
1
−b
a
0
1
1
b
y
x
A1
−c
Тогда координаты точки A1(a; −b; −c).
5.
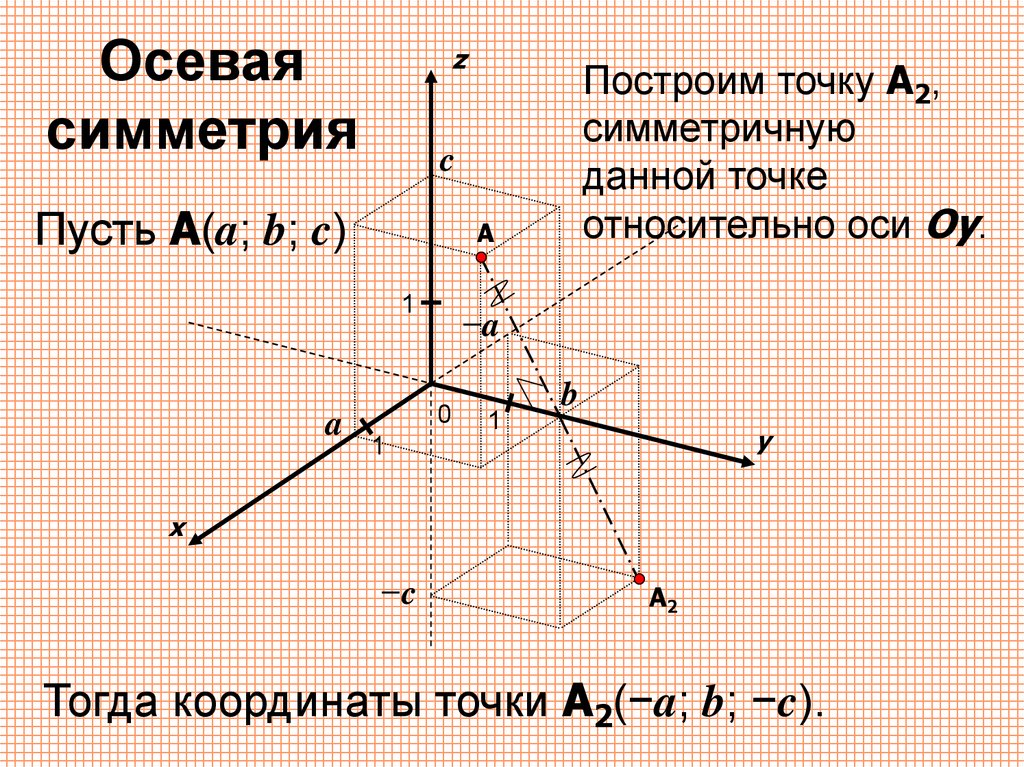
Осеваясимметрия
z
c
Пусть A(a; b; c)
A
1
a
Построим точку A2,
симметричную
данной точке
относительно оси Oy.
−a
0
1
b
y
1
x
−c
A2
Тогда координаты точки A2(−a; b; −c).
6.
Осеваясимметрия
Построим точку A3,
симметричную данной
точке относительно
оси Oz.
z
A3
c
Пусть
A(a; b; c)
A
1
−a
−b
a
0
1
1
b
y
x
Тогда координаты точки A3(−a; −b; c).
7.
Зеркальнаясимметрия
z
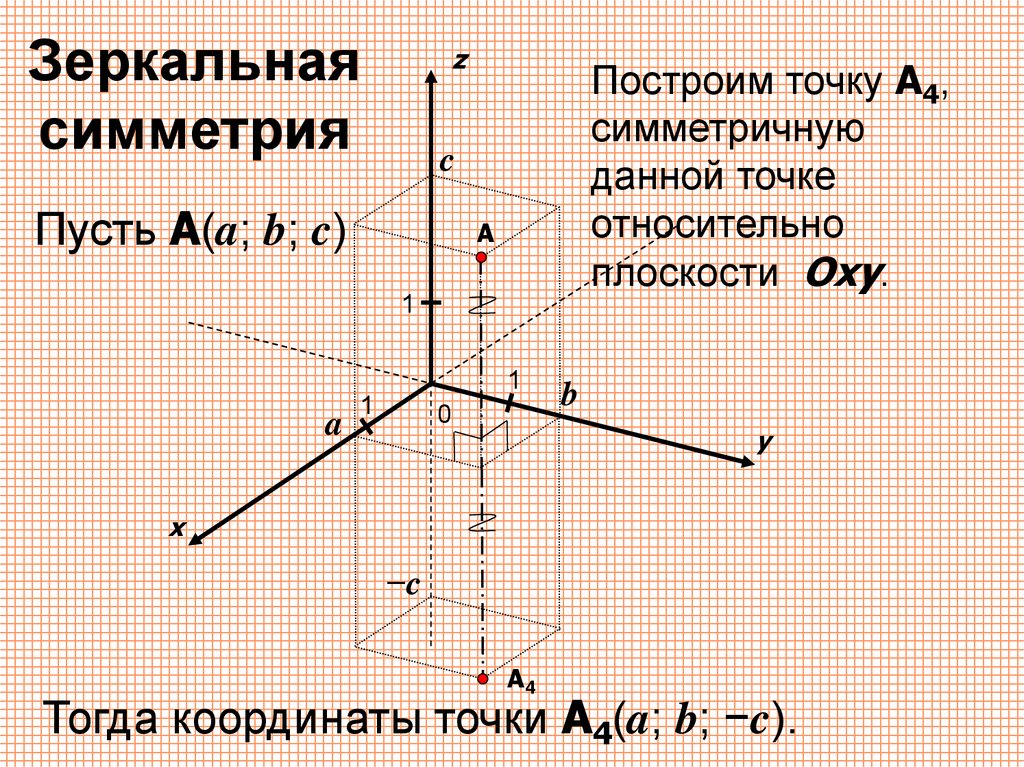
Построим точку A4,
симметричную
данной точке
относительно
плоскости Oxy.
c
Пусть A(a; b; c)
A
1
1
a
1
0
b
y
x
−c
A4
Тогда координаты точки A4(a; b; −c).
8.
Зеркальнаясимметрия
z
c
A5
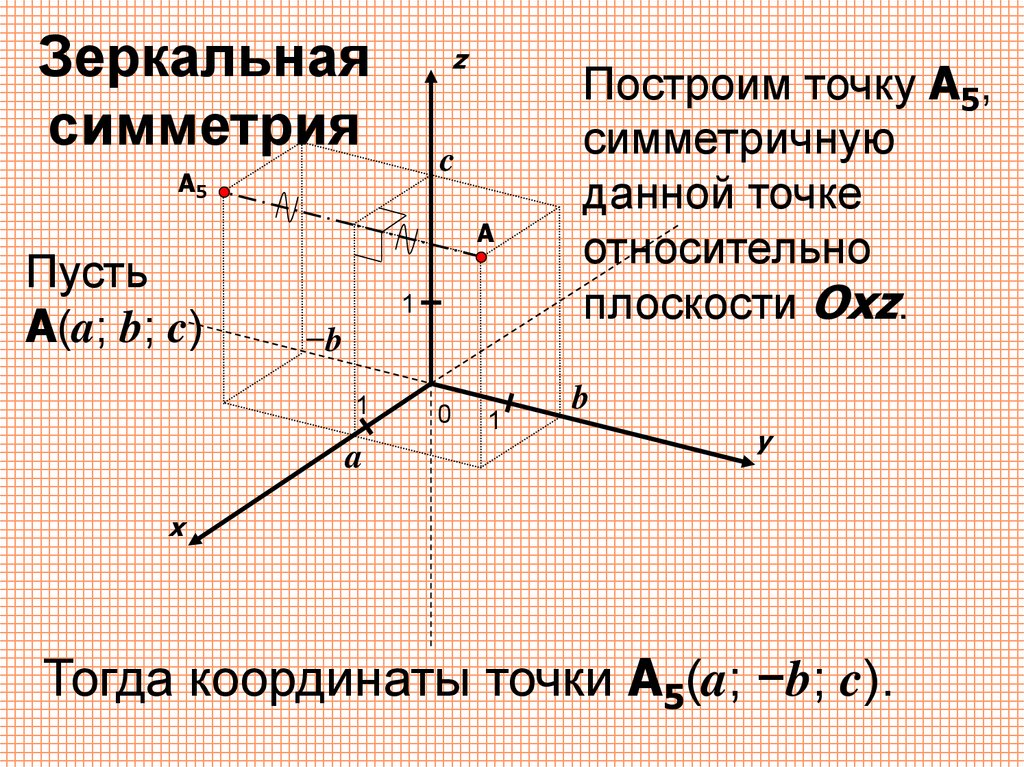
Пусть
A(a; b; c)
A
1
−b
1
a
0
1
Построим точку A5,
симметричную
данной точке
относительно
плоскости Oxz.
b
y
x
Тогда координаты точки A5(a; −b; c).
9.
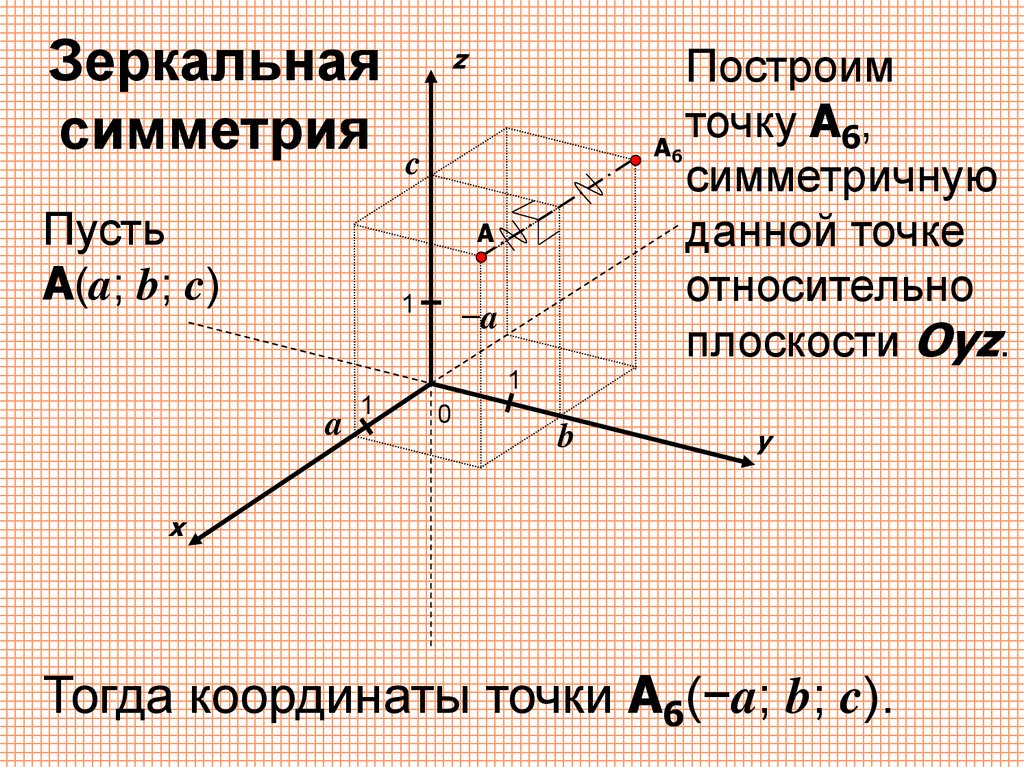
Зеркальнаясимметрия
Пусть
A(a; b; c)
Построим
точку A6,
A
симметричную
данной точке
относительно
плоскости Oyz.
z
6
c
A
1
−a
1
a
1
0
b
y
x
Тогда координаты точки A6(−a; b; c).




 Математика
Математика








