Похожие презентации:
Элементы комбинаторики (часть 1)
1.
Элементыкомбинаторики
9 класс
Часть 1
г.Москва, НЧУ ОО ЦПШ
«Косинская»,
учитель математики
Клейникова
Виктория Германовна
Учебник «Алгебра. 9 класс»
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. под
редакцией Теляковского С.А., М.: Просвещение.
2.
Содержание1
Что такое «комбинаторика»?
2
Примеры комбинаторных задач
3
Комбинаторные правила
4
Решаем на уроке
5
Домашнее задание
3.
Что такое «комбинаторика»?• Комбинаторика – это раздел математики,
посвященный задачам выбора и
расположения элементов некоторого (обычно
конечного) множества в соответствии с
заданными правилами.
• Комбинаторные задачи – это задачи на
перебор всех возможных вариантов.
4.
Примеры комбинаторныхзадач
ПРИМЕР 1. В кафе предлагают два первых блюда: борщ, рассольник
– и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
Укажите все обеды, которые может заказать посетитель.
Решение.
Введем обозначения: Б – борщ, Р – рассольник;
Г – гуляш, К – котлеты, С – сосиски, П – пельмени.
Составим все возможные пары из первого и второго блюд:
БГ
РГ
1-ый способ –
БК
РК
БС
РС
перебор всех
БП
РП
вариантов.
ИТОГО: 8 обедов.
5.
Примеры комбинаторныхзадач
ПРИМЕР 1. В кафе предлагают два первых блюда: борщ, рассольник
– и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
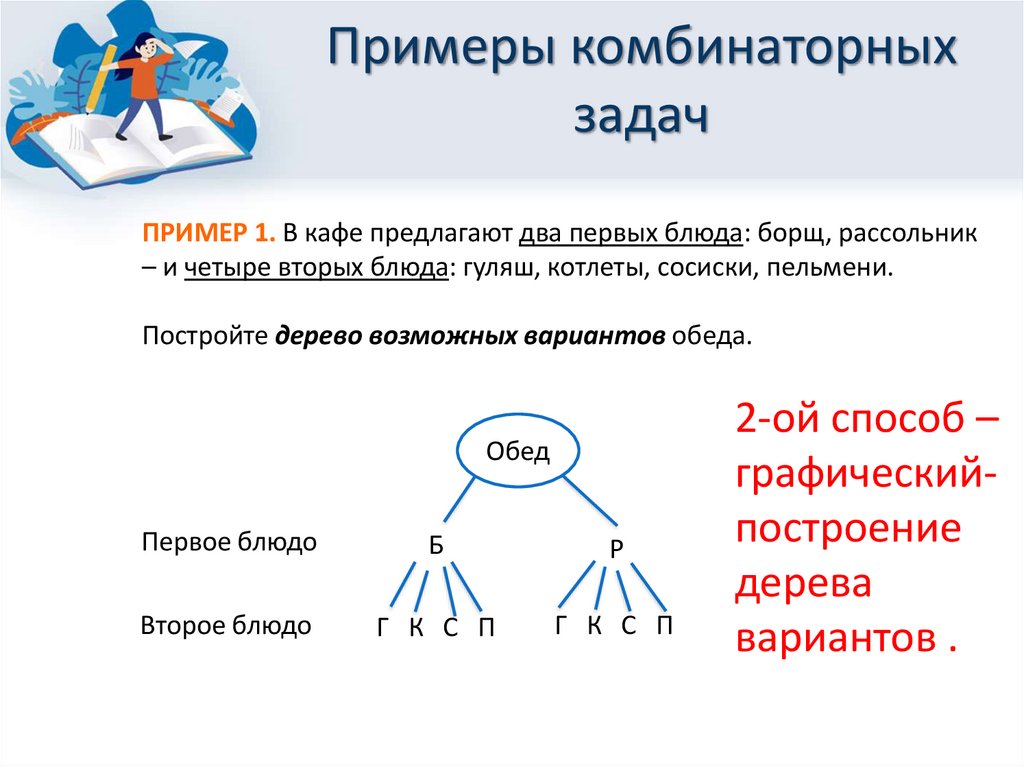
Постройте дерево возможных вариантов обеда.
Обед
Первое блюдо
Б
Р
Второе блюдо
Г К С П
Г К С П
2-ой способ –
графическийпостроение
дерева
вариантов .
6.
Примеры комбинаторныхзадач
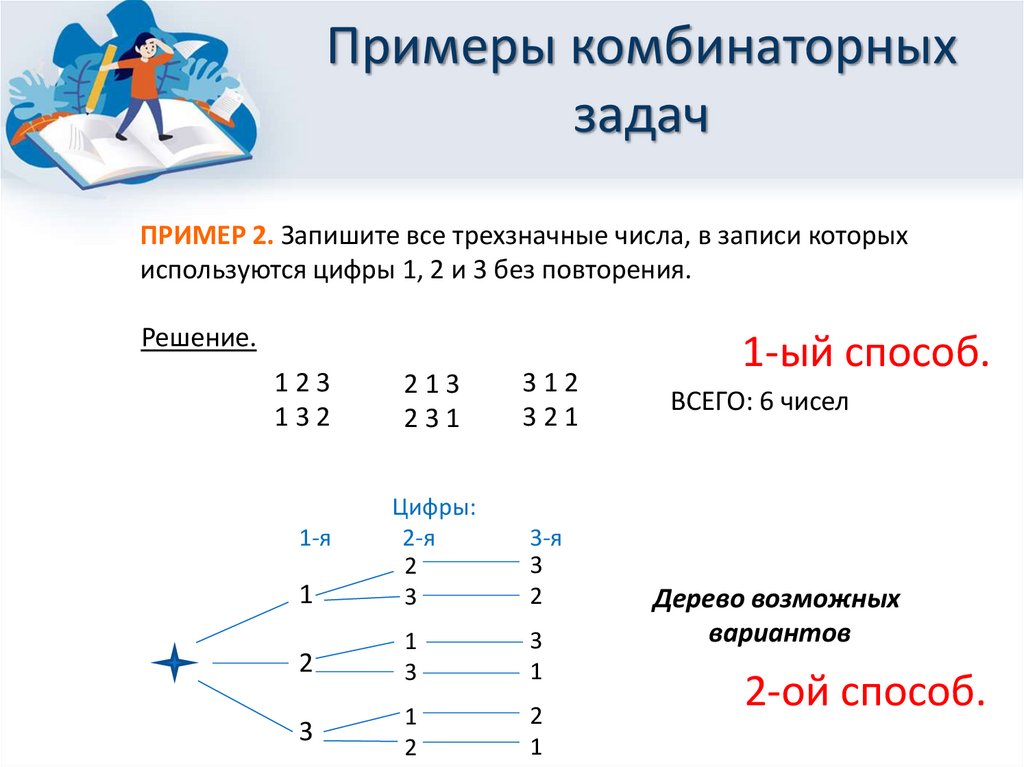
ПРИМЕР 2. Запишите все трехзначные числа, в записи которых
используются цифры 1, 2 и 3 без повторения.
Решение.
123
132
1-я
1
213
231
312
321
Цифры:
2-я
2
3
3-я
3
2
2
1
3
3
1
3
1
2
2
1
1-ый способ.
ВСЕГО: 6 чисел
Дерево возможных
вариантов
2-ой способ.
7.
Примеры комбинаторныхзадач
ПРИМЕР 3. Какие двузначные числа можно записать, используя
цифры 1, 2 и 3 ?
Решение.
11
12
13
21
22
23
ВСЕГО: 9 чисел
31
32
33
1-ый способ.
8.
Комбинаторные правилаВернемся к примеру 1.
ПРИМЕР 1. В кафе предлагают два первых блюда: борщ, рассольник
– и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
Сколько различных обедов может заказать посетитель?
Решение.
С каждым первым блюдом может сочетаться
4 вторых блюда. Так как первых блюд 2, то
чтобы посчитать число всех возможных
комбинаций, надо 2 умножить на 4 :
2 · 4 = 8 (обедов)
3-ий способ –
использование
правил
и формул.
Правило умножения. Если имеется m способов выбрать элемент a
и n способов выбрать элемент b , то пару (a,b) можно выбрать
m · n способами.
9.
Комбинаторные правилаС помощью правила умножения решим
ПРИМЕР 3. Сколько двузначных чисел можно записать, используя
цифры 1, 2 и 3 ?
3-ий способ.
Решение.
Имеем 3 способа выбрать 1-ую цифру числа и 3 способа
выбрать 2-ую цифру числа. По правилу умножения всего
можно записать:
3 · 3 = 9 (чисел)
10.
Комбинаторные правилаПравило умножения можно обобщить для большего числа
элементов.
Правило умножения (в общем виде). Если имеется m способов
выбрать элемент a , n способов выбрать элемент b , … , k способов
выбрать элемент t , то набор (a, b, …, t) можно выбрать
m · n · … · k способами.
11.
Комбинаторные правилаС помощью правила умножения решим
ПРИМЕР 2. Сколько существует трехзначных чисел, в записи которых
используются цифры 1, 2 и 3 без повторения?
Решение.
Первой цифрой может быть любая из 3-х цифр, второй
цифрой – любая из 2-х оставшихся цифр, третьей цифрой –
одна цифра.
По правилу умножения количество чисел, в записи которых
используются цифры 1, 2 и 3 без повторения, равно:
3·2·1=6
3-ий способ.
12.
Комбинаторные правилаПРИМЕР 4. В классе 12 мальчиков и 15 девочек. Сколькими
способами можно выбрать одного человека из класса на
общешкольную конференцию?
Решение.
12 + 15 = 27 (способов)
Правило сложения. Если имеется m способов выбрать элемент a
и (независимо от них) n способов выбрать элемент b , то выбрать
один элемент – или a, или b - можно m + n способами.
Аналогичное правило применяется и для большего числа
элементов.
13.
Комбинаторные правила(обобщение)
И a, и в
Или a, или в
Правило
умножения
Правило
сложения
Если имеется m способов
выбрать элемент a и n
способов выбрать элемент b ,
то выбор a и b можно сделать
m · n способами.
Если имеется m способов
выбрать элемент a и n способов
выбрать элемент b , то выбор
a или b можно сделать
m + n способами.
14.
Решаем на уроке№ 715 с. 185
№ 716
№ 718
15.
Сегодня на уроке узнали:Что такое «комбинаторные задачи»?
Какие правила применяются для решения
комбинаторных задач?
Какие способы используются для решения
комбинаторных задач?
16.
Домашнее задание№№ 719, 726, 727
с. 185
17.
Решаем на урокеЗадача.
При встрече 5 человек обменялись рукопожатиями.
Сколько всего было сделано рукопожатий?
Решение.
1-ый способ.
Б
АБ
АВ
АГ
АД
В
А
Сосчитаем отрезки.
ВГ
ВД
ГД
4 + 3 + 2 + 1 = 10 (рукопожатий)
Г
2-ой способ.
БВ
БГ
БД
Д
3-ий способ.
5 · 4 : 2 = 10
18.
Решаем на уроке№ 722 с. 186
В соревнованиях по футболу участвовало 12 команд. Каждая команда
провела с каждой из остальных по одной игре на своем поле и по одной
игре на поле соперника. Сколько игр всего было сыграно?
Решение.
3-ий способ.
Чем эта задача отличается от предыдущей?
12 · 11 = 132 (игры)
19.
Решаем на урокеЗадача
Государственные регистрационные номера состоят из буквы, трех цифр,
еще двух букв и номера региона. Буквы и цифры могут повторяться.
Можно использовать только 12 букв: А, В, Е, К, М, Н, О, Р, С, Т, У, Х.
Цифры можно брать любые от 0 до 9. В качестве номера для
московских автомобилей используется одно из чисел 77, 97, 99, 177,
197, 199, 777, 799.
Сколько всего можно составить регистрационных номеров для
автомобилей в Москве?
Решение.
12 ·10 · 10 · 10 · 12 · 12 · 8 =
123 · 103 · 8 = 13 824 000
3-ий способ.
20.
Домашнее задание№№ 720, 721
с. 185


















 Математика
Математика








