Процент. Сокращенные процентные соотношения. Задачи на проценты

1.

Задачи на проценты.
Аттар Лариса Борисовна, учитель математики ГБОУ школы 588

2.

Содержание
1. Процент . Сокращенные процентные
соотношения.
2. Разминка.
3. Основные задачи на проценты:
Нахождение процентов числа.
Нахождение числа по его процентам
Нахождение процентного отношения двух чисел
4. Задачи на смеси.

3.

Процент
Проце́нт (нем. Prozent, от
новолат. per centum «на сотню;
сотая») — сотая часть;
обозначается знаком «%»;
используется для обозначения доли
чего-либо по отношению к целому
https://ru.wikipedia.org/

4.

Сокращенные процентные
соотношения
1% = 1/100
100% = 1
10% = 1/10
50% = ½
5% = 1/20
25% = 1/4
200% = 2

5.

Задание 1. Какие из утверждений означают
одно и то же:
величины относятся как 1:2
А) одна величина вдвое меньше другой;
Б) вторая величина на 300% больше первой;
В) вторая величина на 100% больше первой;
Г) одна величина составет от другой 50%;

6.

Задание 2.
50% от 200р =……..
150р.
250р.
100р.

7.

Задание 3. Установите соответствие
7%
16%
113%
0,4%
25%
0,04
0,25
0,07
0,16
1,13

8.

Основные задачи на проценты
р % = 0,01р = р/100
1. Нахождение процентов данного числа.
Чтобы найти р % от а, надо а·0,01р
2. Нахождение числа по его процентам.
Если известно, что р% числа равно b,
то
а = b: 0,01р
3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо
отношение этих чисел умножить на 100%
а/b ·100

9.

Задание 4. Произвести расчеты
1. Найти 25% от 56
14
2. Сколько % составит 30 от 75?
40
3.Найдите число, 20% которого равны 12
4. Какое число, увеличенное на 13%
составит 339?
60
300
5. В избирательном округе нашего посёлка 1005 человек. В
голосовании приняло 40%.Сколько человек голосовало?
402
Банк начисляет на вклад ежегодно 8% от вложенной суммы.
Сколько рублей будет начислено через год на вклад в 5000 р.?
400 р.

10.

Задание 5
• Выполните тест:

11.

12.

13.

ЗАДАЧА 1.
При оплате услуг через платежный терминал
взимается комиссия 5%. Терминал принимает
суммы кратные 10 рублям. Аня хочет
положить
на
счет
своего
мобильного
телефона не менее 300 рублей. Какую
минимальную сумму она должна положить в
приёмное устройство данного терминала?
Решение: 300 · 0,05= 15 (р) – комиссия
300+15 = 315 (р) – можно положить
320 р. надо положить на счёт
Ответ:320р.

14.

ЗАДАЧА 2.
На покупку планшета взяли кредит 20000 р. на
1 год под 20 % годовых . Вычислите, сколько
денег необходимо вернуть банку? Какова
ежемесячная сумма выплат?
Решение : 20000 · 0,20 = 4000(р) составляют
проценты
20000 + 4000 = 24000 (р) вся сумма выплат
24000:12= 2000(р)- за 1 месяц
Ответ:24000р., по 2000р.в месяц.

15.

ЗАДАЧА 3.
Мобильный телефон стоил 5000 рублей. Через
некоторое время цену на эту модель снизили
до 3000 рублей. На сколько процентов была
снижена цена?
Решение:
5000 – 3000 = 2000(р) – на столько снижена
цена на телефон
(2000: 5000) · 100% = (2:5) · 100% = 0,4 · 100 =
=40 % на столько снижена цена
Ответ: на 40 %.

16.

Задачи для дополнительного решения:
1.В магазине цены были сначала повышены на 10%, а
потом снижены на 10%. Как изменились цены?
2.На сколько процентов новая цена меньше старой и на
сколько процентов старая цена больше новой, если:
Цена снижена наполовину;
Цена повышена наполовину;
Цена увеличена в 4 раза;
Цена уменьшена в 3 раза?
3.Фирма платит рекламным агентам 5% от стоимости
заказа. На какую сумму надо найти заказ, чтобы
заработать 1000р.?
4.Предприниматель покупает кондитерские изделия по
оптовой цене 96 р. и продает их в розницу с надбавкой в
30%. Какова розничная цена?

17.

5.Владелец дискотеки имел стабильный доход. В
погоне за прибылью он увеличил цену на билеты на
25%. Количество посетителей резко уменьшилось, и он
стал нести убытки. Тогда он вернулся к
первоначальной цене билетов. На сколько процентов
владелец дискотеки снизил новую цену билетов, чтобы
она стала первоначальной?
6.После уплаты всех налогов, которые в сумме
составили 30% от дохода, предприниматель оставил
себе на законном основании 35000р.Какова была
величина чистого дохода предпринимателя?
7.В Санкт-Петербурге месячный проездной билет для
студентов стоит 350р. Сколько процентов составляет
от стипендии цена проездного билета, если стипендия 900р.?

18.

8.Владелец дискотеки имел стабильный доход. В
погоне за прибылью он увеличил цену на билеты на
25%. Количество посетителей резко уменьшилось, и он
стал нести убытки. Тогда он вернулся к
первоначальной цене билетов. На сколько процентов
владелец дискотеки снизил новую цену билетов, чтобы
она стала первоначальной?
9.После уплаты всех налогов, которые в сумме
составили 30% от дохода, предприниматель оставил
себе на законном основании 35000р.Какова была
величина чистого дохода предпринимателя?
10.В Санкт-Петербурге месячный проездной билет для
студентов стоит 350р. Сколько процентов составляет
от стипендии цена проездного билета, если стипендия
-900р.?

19.

11.В одном магазине на товар установили цену 200р., а в другом
аналогичный товар стоит 180р.
а) На сколько процентов в первом магазине цена на товар выше,
чем в первом?
б)На сколько процентов во втором магазине цена ниже, чем в
первом?
12.Первоначально цена на аналогичный товар в двух магазинах
была одинакова.
В первом магазине цену сначала снизили
на 20%, а потом еще на 20%, а во втором магазине ее сразу
снизили на 40%. Одинаковы ли стали цены в магазинах?
13.Цена на бензин в первом квартале увеличилась на 20%, а во
втором- на 30%. На сколько процентов увеличилась цена на
бензин за два квартала?
14.Зарплату рабочему повысили на 10%, а через год еще на 20%.
На сколько процентов повысилась зарплата по сравнению с
первоначальной?
15.Определите первоначальную стоимость продукта, если после
подорожания на 120%,200%,100% его конечная стоимость
составила 264р.?

20.

Задачи по теме «Проценты» по банковским операциям
1.Банк выплачивает вкладчикам каждый год 8% от
внесенной суммы. Клиент сделал вклад в размере
200000р. Какая сумма будет на его счете через 5 лет.
Через 10 лет?
2.При какой процентной ставке вклад на сумму 55р.
Возрастет за 6 месяцев до 650р.
3.Каким должен быть начальный вклад, чтобы при ставке
4% в месяц он увеличился за 8 месяцев до 33000р.
4.Вкладчик открыл счет в банке, внеся 200р. На вклад,
годовой доход по которому составляет 12%, и и решил в
течение 6 лет не брать процентные начисления. Какая
сумма будет лежать на его счете через 6 лет?
5.Каким должен быть первоначальный капитал, чтобы при
начислении 5% в месяц получить через полгода 10000р.?
Какой должна быть процентная ставка в банке, чтобы
каждые три года капитал увеличивался в 4 раза?

21.

Задачи по теме «Проценты» геометрического содержания.
1.Каждую сторону квадрата увеличили на 20%.
На сколько процентов увеличилась площадь
квадрата?
2.На сколько процентов увеличится объем
куба, если его ребро увеличили на 10%.
3.Длину прямоугольника уменьшили на 20%.
На сколько процентов надо увеличить ширину
прямоугольника, чтобы его площадь не
изменилась?

22.

Задачи по теме «Проценты» произвольного содержания.
1.Произведение двух чисел равно 10, а их сумма составляет 70% от
произведения. Найдите эти числа.
2.В одном из городов часть жителей умеет говорить только по-грузински,
часть только по-русски. По-грузински говорят 85% всех жителей, а по-русски75%. Сколько процентов всех жителей говорят на обоих языках?
3.Ученик прочитал в первый день 15% всей книги, что составило 60 страниц,
во второй день прочитал 200страниц. Сколько страниц ему осталось
прочитать?
4.Сравните числа а и в, если 3% числа а равны 27, а 5% числа в равны 45.
Определите, какую массу картофеля (сырья) нужно взять для получения
120кг полуфабриката, если потери при холодной обработке составляют 20%
массы сырья.
5.В двух бочках было воды поровну. Количество воды в первой бочке сначала
уменьшили на 10%, а затем увеличили на 10%. Количество воды во второй
бочке сначала увеличили на 10%, а затем уменьшили на 10%. В какой бочке
стало больше воды?
6.За три года население города увеличилось с 2000000 до 2315250 человек.
Найдите годовой прирост населения в процентах.
7.Производительность труда на заводе снизилась на 20%. На сколько
процентов ее надо повысить, чтобы достигнуть первоначальной?

23.

Задачи по теме «Проценты» с историческими сюжетами.
1.
Завещание Бенджамина Франклина: «Препоручаю 1000
фунтов стерлингов бостонским жителям. Если они примут эту
тысячу фунтов, то должны поручить ее отборнейшим гражданам,
а они будут давать ее с процентами по 5 на 100 в год в заем
молодым ремесленникам. Сумма эта через 100 лет возвысится
до 131000 фунтов. Я желаю, чтобы тогда 100000 фунтов
употреблены были на постройку общественных зданий, а
остальные 31000 фунтов отданы были в проценты на 100 лет. По
истечении второго столетия сумма возрастет до 4061000 фунтов,
из коих 1061000 фунтов оставляю в распоряжение бостонских
жителей, а 3000000 фунтов правлению Массачусетской общины.
Далее не осмеливаюсь простирать своих видов».мы видим, что
завещав всего 1000 фунтов, Б.Франклин распоряжается
миллионами. Проверьте, не ошибся ли он в своих расчетах.

24.

25.

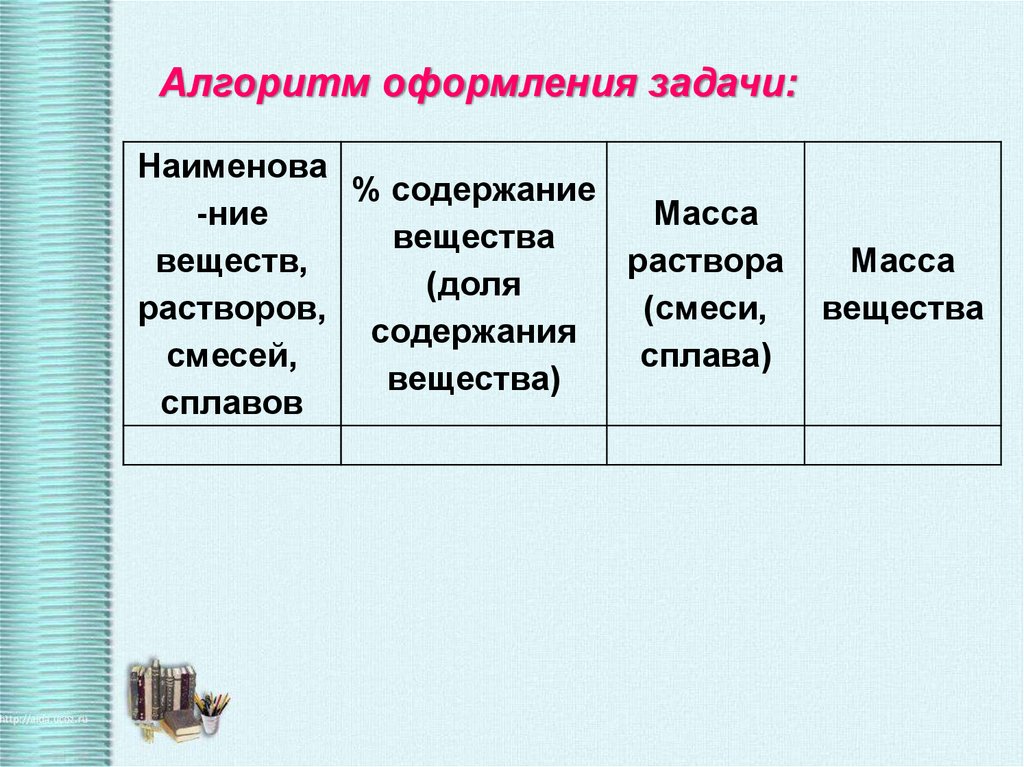
Алгоритм оформления задачи:
Наименова
% содержание
-ние
Масса
вещества
веществ,
раствора
(доля
растворов,
(смеси,
содержания
смесей,
сплава)
вещества)
сплавов
Масса
вещества

26.

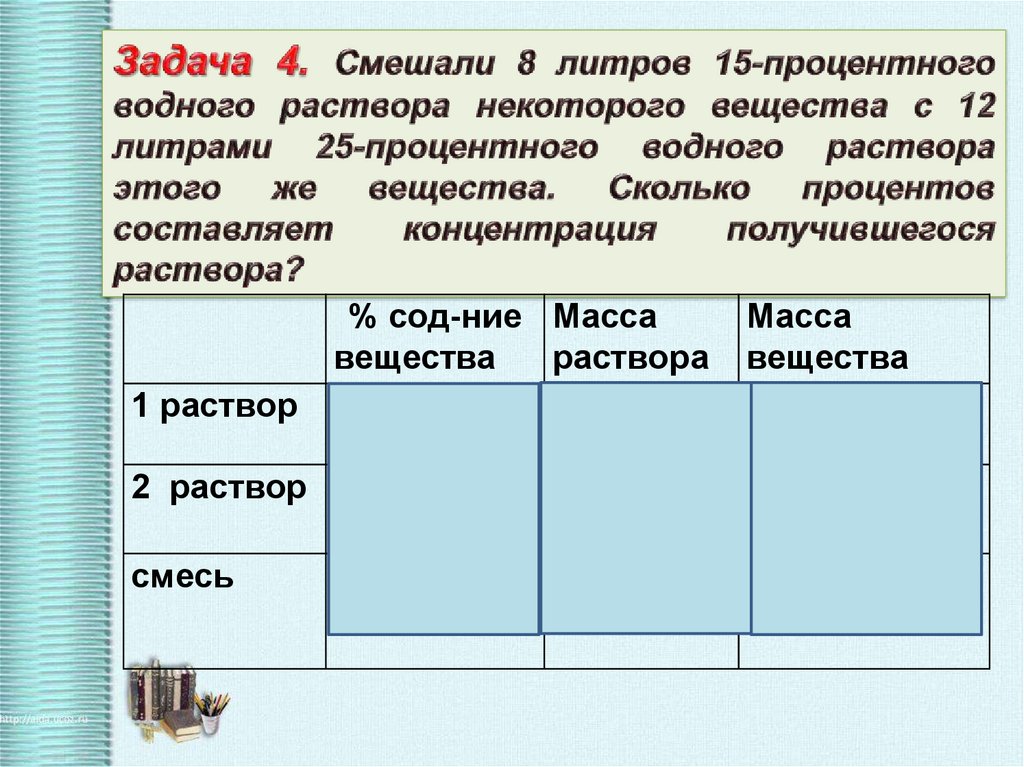
1 раствор
% сод-ние Масса
вещества
раствора
15% = 0,15
8 л.
Масса
вещества
8 ∙0,15 =1,2л.
2 раствор 25% = 0,25
12 л.
12 ∙ 0,25 =3л.
смесь
20 л.
4,2л.

27.

Решение.
С =(m вещества : m раствора)·100%
где, С-концентрация раствора
С=( 4,2 : 20)·100%= 21%
Ответ: 21%.

28.

. Один раствор содержит 20 %
соли, а второй – 70 %. Сколько
граммов первого и второго раствора
нужно взять, чтобы получить 100 г
50% раствора.
.
% сод-ние Масса
Масса
вещества раствора вещества
1 раствор 20%=0,2
х гр.
0,2х гр.
2 раствор 70%=0,7
у гр.
0,7у гр.
смесь
50%=0,5
100 гр..
0,2х+0,7у гр..

29.

Решение.
50% от 100гр = 50 гр.
{
Система уравнений:
х + у = 100
0,2х + 0,7 у = 50

30.

Первый сплав содержит 10 %
меди, второй - 25 % меди. Из
этих двух сплавов получили
третий сплав массой 3 кг,
содержащий 20 % меди. Какое
количество каждого сплава было
использовано?

31.

1способ % содержания Масса
вещества
Масса меди
сплава
1 сплав
10% = 0,1
Х
кг.
2 сплав
25% = 0,25
У
кг.
сплав
20 % = 0,2
3
кг.
0,1 х кг.
0,25 у кг.
3 ∙ 0,2=0,6 кг.
0,1х + 0,25у = 3 ∙ 0,2
х + у = 30
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
х =3-у
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
0,15 у = 0,3
у = 2 , значит
х = 1.
Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.

32.

% содержания Масса
2 способ вещества
сплава
Масса меди
1 сплав 10% = 0,1
0,1 х
( 3 – х) ∙ 0,25
2 сплав 25% = 0,25
сплав
20 % = 0,2
х кг
(3-х)
кг
3 кг
3 ∙ 0,2
х ∙ 0,1 + ( 3 - х ) ∙ 0,25 = 3 ∙ 0,2
х ∙ 0,1 + 0,75 - х ∙ 0,25 = 0,6
- 0,15 х = - 0,15
х = 1, значит 3 – 1 = 2.
Ответ: 1 сплав – 1 кг,
2 сплав – 2 кг

33.

3 способ
По формуле
m1·p1 +m2·p2 +…+ mn· p =p(m1+ m2 + … + mn ),
n
где m1, m2 , m-nмассы растворов, Р –процентное
содержание нового раствора, p1 и p2, p-n процентное
содержание растворов.
Решение:
Пусть масса первого раствора Х кг, масса второго
раствора у кг. Используя формулу составим систему
уравнений.
10(3-х)+25у=60
15у=30
10х +25у =20·3
У=2
Х + у =3
Х=3-2=1
10х +25у =60
Ответ:1 сплав – 1 кг,
Х =3-у
2 сплав – 2 кг.

34.

Задача 7
При смешивании первого раствора кислоты,
концентрация которого 20%, и второго раствора этой
же кислоты, концентрация которого 50%, получился
раствор, содержащий 30% кислоты.
В каком отношении были взяты первый и второй
растворы?
Решение.
х
20%=1/5
получили
у
х+у
50%=1/2
Составим уравнение:
1/5 ·х + 1/2·у = 3/10·(х + у)
30%=3/10

35.

Решаем уравнение:
1/5·х + 1/2·у = 3/10·(х + у)
1/5·х + 1/2·у = 3/10·х + 3/10·у
1/5·х - 3/10·х = 3/10·у - 1/2·у
х (1/5 - 3/10) = у (3/10 - 1/2 )
Надо найти отношение первого и второго
растворов, т.е. как х : у, поэтому уравнение
делим на у:
Получаем: х/у ·(-1/10) = -1/5
х/у = (-1/5) : (-1/10) = -1/5 · (-10/1) = + 2
Значит х : у = 2:1
Ответ: 2:1

36.

Задачи по теме «Проценты» на растворы, сплавы, смеси.
1.
Сколько граммов воды можно выпарить из 80г 6%го раствора соли, чтобы получить раствор, содержащий
10% соли?
2.
Имеется два кислотных раствора: один 20%,
другой 30%.Взяли 0,5л первого и 1,5л второго и
образовали новый раствор. Какова концентрация кислоты
в новом растворе?
3.
Смешали 300г 50% и 100г 30% раствора кислоты.
Определите процентное содержание кислоты в
полученной смеси.
4.
Сколько чистой воды надо добавить к 300г
морской воды, содержащей 4% соли, чтобы получить воду,
содержащую 3% соли?
5.
Имеется два сосуда, содержащие 4кг и 6кг
раствора кислоты различной концентрации. Если их слить
вместе, то получим раствор, содержащий 35% кислоты.
Если же слить равные массы этих растворов, то получим
раствор, содержащий 36% кислоты. Сколько килограммов
кислоты содержится в каждом растворе?

37.

6.
имеется два раствора серной кислоты в воде, первый 40%,
второй 60%. Эти растворы смешали, после чего добавили5 кг чистой
воды и получили 20% раствор кислоты. Если бы вместо 5кг воды
добавили 5кг 80% раствора, то получили бы 70% раствор. Определите
количество 40% и 60% раствора.
7.
Имеются две смеси апельсинового и ананасового соков.
Первая смесь содержит 40% апельсинового сока, а вторая -80%.
Сливаются р литров первой смеси и g литров второй, в результате
получается 20л смеси, содержащей 70% апельсинового сока.
Определите р и g.
8.
Имеется раствор№1 и раствор №2 некоторой кислоты в воде.
При смешивании 5л раствора №1, 6л раствора №2 и 3л чистой воды
получается раствор с концентрацией кислоты, равной 30%. При
смешивании 10л раствора№1, 3л расивора№2 и 2л чистой воды
получается раствор с концентрацией кислоты равной 33 %.
Определите α- и β- концентрации раствора№1 и раствора № 2
соответственно.
9.
Сколько граммов воды надо добавить к 50г раствора,
содержащего 8% соли, чтобы получить 5% раствор?

38.

10.
Сколько граммов 30%-го раствора надо добавить к 80г
12%-го раствора этой же соли, чтобы получить 20% раствор
соли?
11.
Кусок сплава меди и цинка массой 36кг содержит 45%
меди. Сколько килограммов меди нужно добавить к этому куску,
чтобы получить новый сплав. Который будет содержать 60%
меди?
12.
Два слитка, один из которых содержит 35% серебра, а
другой 65%, сплавляют и получают слиток массой 30г,
содержащий 47% серебра. Какова масса каждого из слитков?
13.
В 500кг руды содержится некоторое количество
железа. После удаления из руды 200кг примесей, содержащих
в среднем 12,5%железа, содержание железа в оставшейся руде
повысилось на 20% Определите, какое количество железа
осталось еще в руде?