Вписанная и описанная окружность

1.

2.

Если все стороны многоугольника касаются
окружности, то окружность называется вписанной
в многоугольник.
А многоугольник
D
С
называется
описанным около
этой окружности.
О
E
В
А

3.

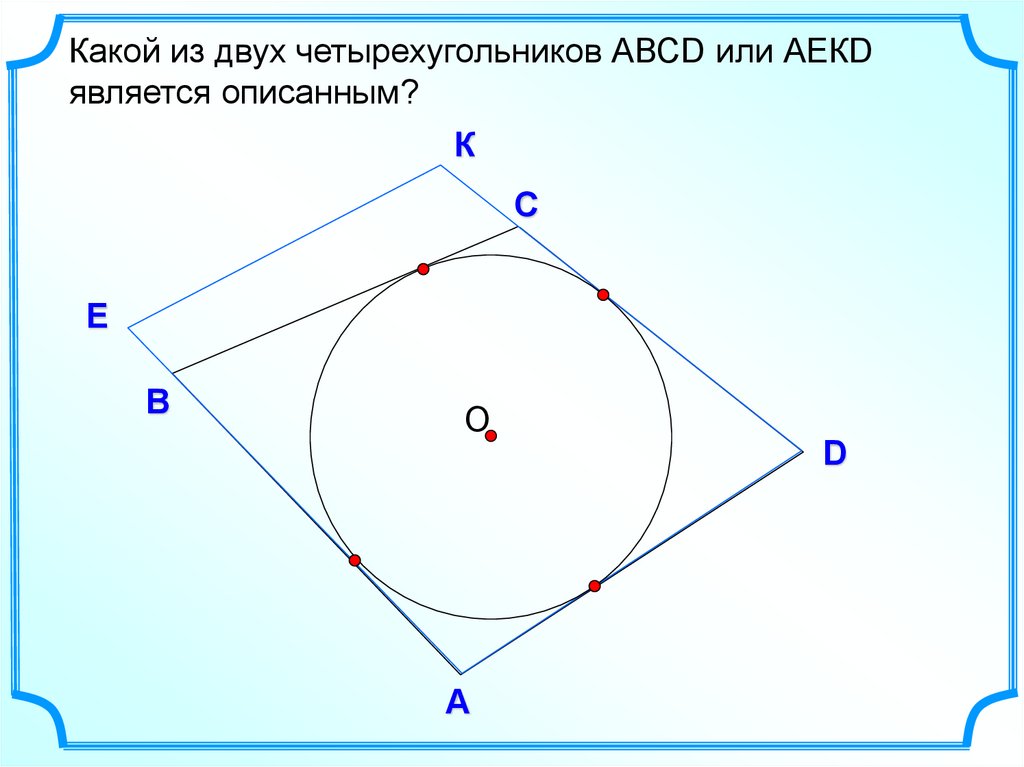
Какой из двух четырехугольников АВСD или АЕКD
является описанным?
К
С
E
В
О
D
А

4.

В прямоугольник нельзя вписать окружность.
С
В
О
А
D

5.

Какие известные свойства нам пригодятся при изучении
вписанной окружности?
Свойство касательной
С
E
Свойство отрезков
касательных
F
В
О
D
P
К
А

6.

В любом описанном четырехугольнике суммы
противоположных сторон равны.
E
d
С
d
R
c
a
В
О
D
c
a
F
N
b
А
b

7.

Верно и обратное утверждение.
Если суммы противоположных сторон выпуклого
четырехугольника равны, то в него можно вписать
окружность.
С
ВС + АD = АВ + DC
В
О
D
А

8.

Теорема
А
В любой треугольник можно
вписать окружность.
Дано: АВС
Доказать, что в
треугольник можно
вписать окружность
С
В

9.

1) ДП: биссектрисы углов треугольника
Проведем из точки О перпендикуляры к сторонам треугольника
2)
СOL = COМ, по гипотенузе и ост. углу
А
ОL = MО
3)
МОА= КОА, по гипотенузе и ост. углу
МО = КО
4) LО=MО=KО
точка О равноудалена от сторон
треугольника. Значит, окружность с
центром в т.О проходит через точки
K, L и M. Стороны треугольника АВС
касаются этой окружности. Значит,
окружность является вписанной
АВС.
В
M
K
О
С
L

10.

Центр окружности,
вписанной в
треугольник, является
точкой пересечения его
биссектрис.
А
О
С
В

11.

Площадь описанного многоугольника
равен половине произведения его
периметра на радиус вписанной
окружности.
a2
В
a1
С
r
r
r
a3
D
О
+ S ВОС
1
a2 r
2
SCOD
…
1
a3 r
2
1
S n (a1 a2 a3 ...) r
2
А
К
S AOB
1
a1 r
2
1
S n Pn r
2
F

12.

Если все вершины многоугольника лежат на
окружности, то окружность называется описанной
около многоугольника.
А многоугольник
С
В
D
О
А
E
называется
вписанным в эту
окружность.

13.

Какой из многоугольников, изображенных на рисунке
является вписанным в окружность?
С
С
D
D
P
В
В
О
О
E
L
А
E
X
А
E

14.

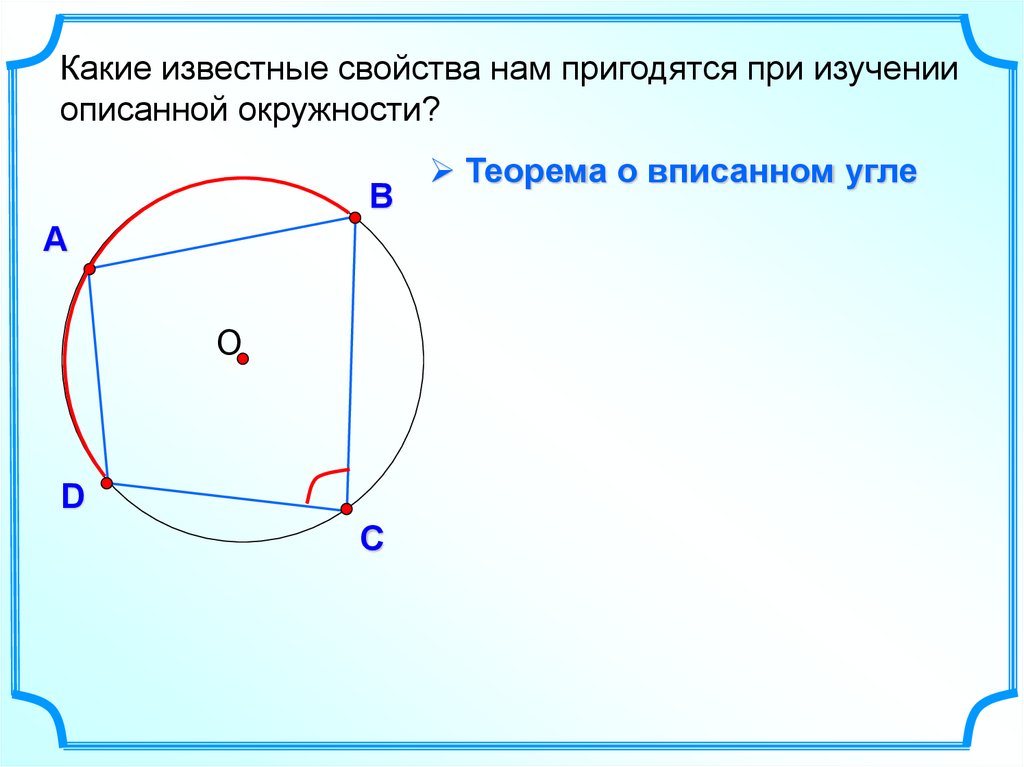
Какие известные свойства нам пригодятся при изучении
описанной окружности?
В
А
О
D
С
Теорема о вписанном угле

15.

В любом вписанном четырехугольнике сумма
противоположных углов равна 1800.
В
А
О
1
А ВCD
2
+
1
C ВAD
2
3600
D
С
1
А С ( ВСD ВАD )
2
А С 1800

16.

Верно и обратное утверждение.
Если сумма противоположных углов
четырехугольника равна 1800, то около него можно
вписать окружность.
В
А
670
А
1000
D
В
990
О
1130
770
О
800
1230
С
D
790
С

17.

Теорема
Около любого треугольника можно
описать окружность.
А
Дано: АВС
Доказать, что можно
описать окружность
С
В

18.

1) ДП: серединные перпендикуляры к сторонам
ВOL = CO L, по катетам ВО = СО
3) СОМ = АOМ, по катетам СО = АО
2)
4) ВО=СО=АО, т.е. точка О
равноудалена от вершин
треугольника. Значит,
окружность с центром в т.О
и радиусом ОА пройдет
через все три вершины
треугольника, т.е. является
описанной окружностью.
А
M
K
С
О
L
В

19.

Центр окружности,
описанной около
треугольника, является
точкой пересечения
серединных
K
перпендикуляров к
сторонам треугольника
А
M
О
С
L
В

20.

Центр описанной
около
остроугольного
треугольника
окружности лежит
внутри
треугольника.

21.

Центром
описанной около
прямоугольного
треугольника
окружности
является середина
гипотенузы.

22.

Центр описанной
около
тупоугольного
треугольника
окружности лежит
вне треугольника.