Правильные многогранники, 10 класс

1. Платновы тела, 10 класс

Правильные
многогранники

2. Определение:

Многогранник
называется правильным,
если все его грани –
равные между собой
правильные
многоугольники

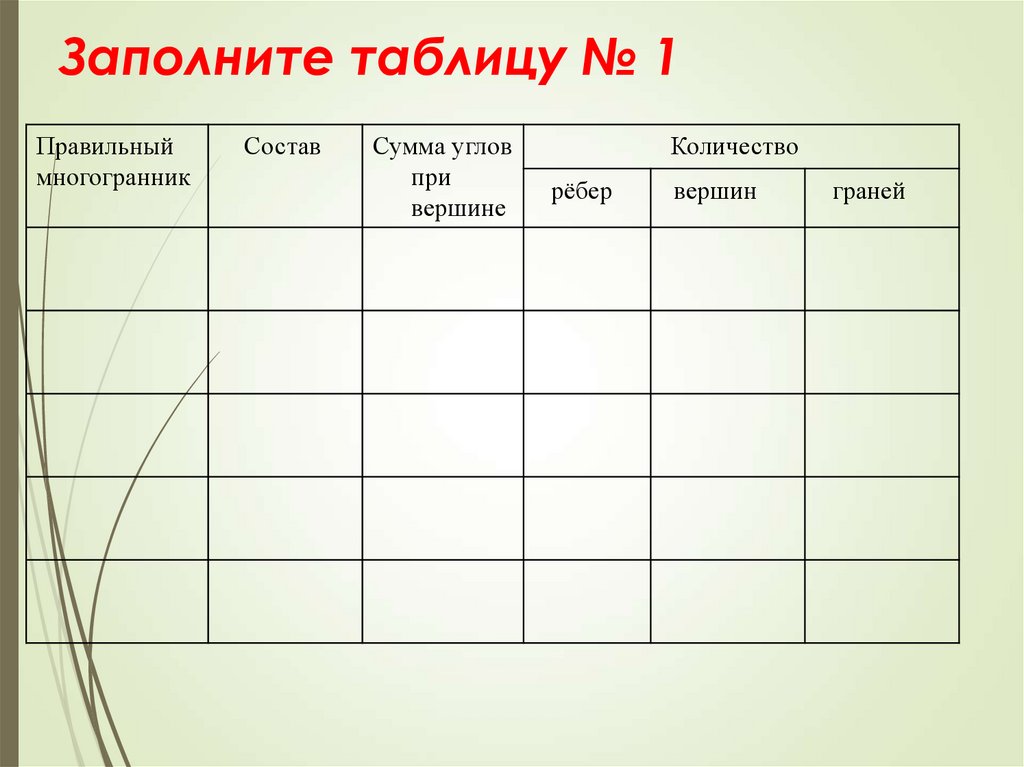
3. Заполните таблицу № 1

Правильный
многогранник
Состав
Сумма углов
при
вершине
Количество
рёбер
вершин
граней

4. тетраэдр

Составлен из четырёх
равносторонних
треугольников. Каждая его
вершина является вершиной
трёх треугольников.
Следовательно, сумма плоских
углов при каждой вершине
равна 180º.
Рис. 1

5.

октаэдр
Составлен из восьми
равносторонних
треугольников. Каждая
вершина октаэдра является
вершиной четырёх
треугольников. Следовательно,
сумма плоских углов при
каждой вершине 240º.
Рис. 2

6.

икосаэдр
Составлен из двадцати
равносторонних треугольников.
Каждая вершина икосаэдра
является вершиной пяти
треугольников. Следовательно,
сумма плоских углов при каждой
вершине равна 300º.
Рис. 3

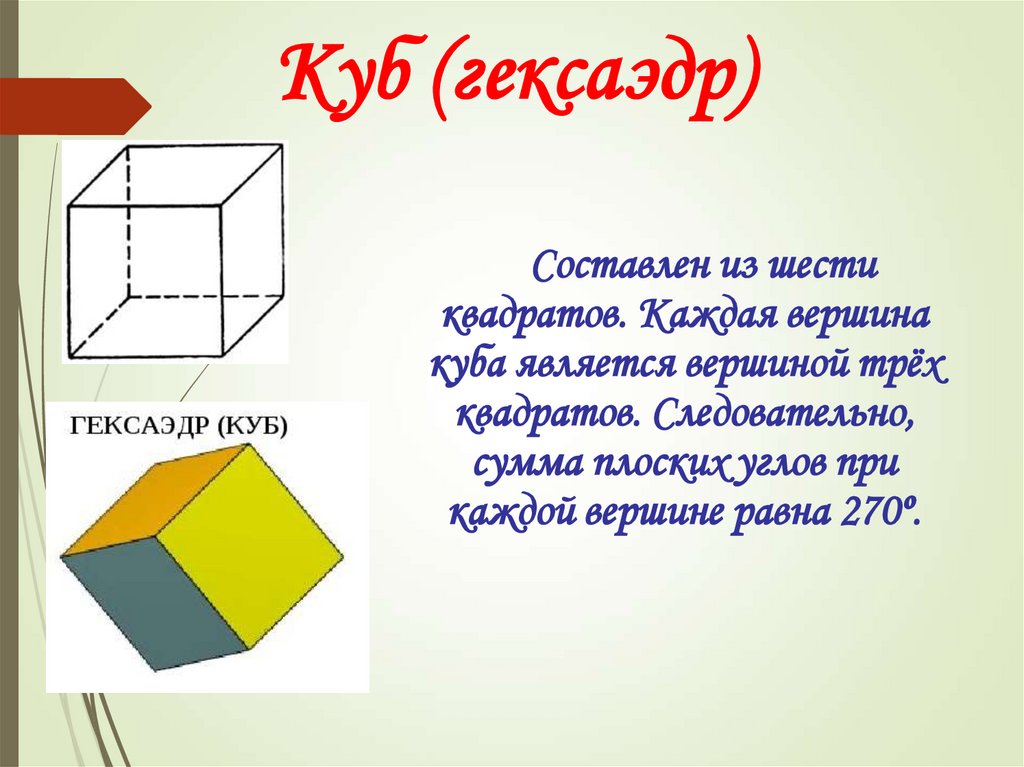
7. Куб (гексаэдр)

Составлен из шести
квадратов. Каждая вершина
куба является вершиной трёх
квадратов. Следовательно,
сумма плоских углов при
каждой вершине равна 270º.
Рис. 4

8.

додекаэдр
Составлен из двенадцати
правильных пятиугольников.
Каждая вершина додекаэдра
является вершиной трёх
правильных пятиугольников.
Следовательно, сумма плоских
углов при каждой вершине
равна 324º.
Рис. 5

9.

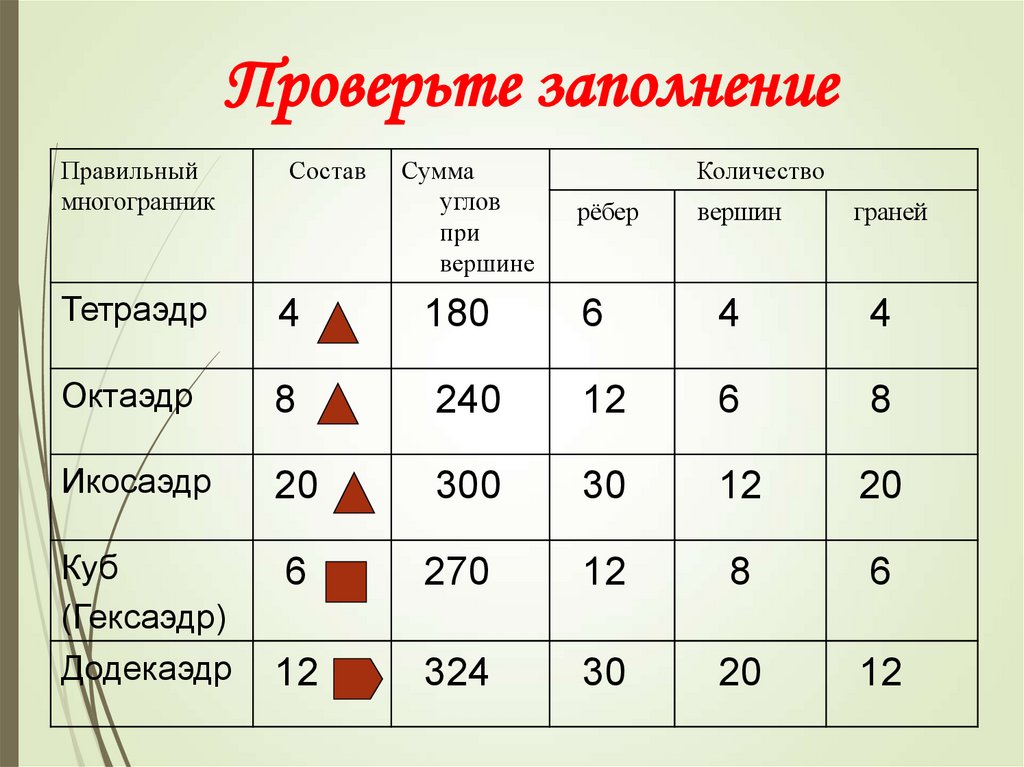
Проверьте заполнение
Правильный
многогранник
Состав
Сумма
углов
при
вершине
Тетраэдр
Количество
рёбер
вершин
граней
4
180
6
4
4
Октаэдр
8
240
12
6
8
Икосаэдр
20
300
30
12
20
Куб
(Гексаэдр)
Додекаэдр
6
270
12
8
6
12
324
30
20
12

10. Названия многогранников

пришли из Древней Греции,
в них указывается число граней:
«эдра» грань;
«тетра» 4;
«гекса» 6;
«окта» 8;
«икоса» 20;
«додека» 12.

11.

Платон (ок. 428 – ок.348 до
н.э.)
Правильные многогранники
иногда называют
платоновыми телами,
поскольку они занимают
видное место в философской
картине мира, разработанвеликим мыслителем
Древней Греции Платоном

12. Платоновы тела

Гексаэдр Тетраэдр Октаэдр Икосаэдр Додекаэдр

13. Правильные многогранники в философской картине мира Платона

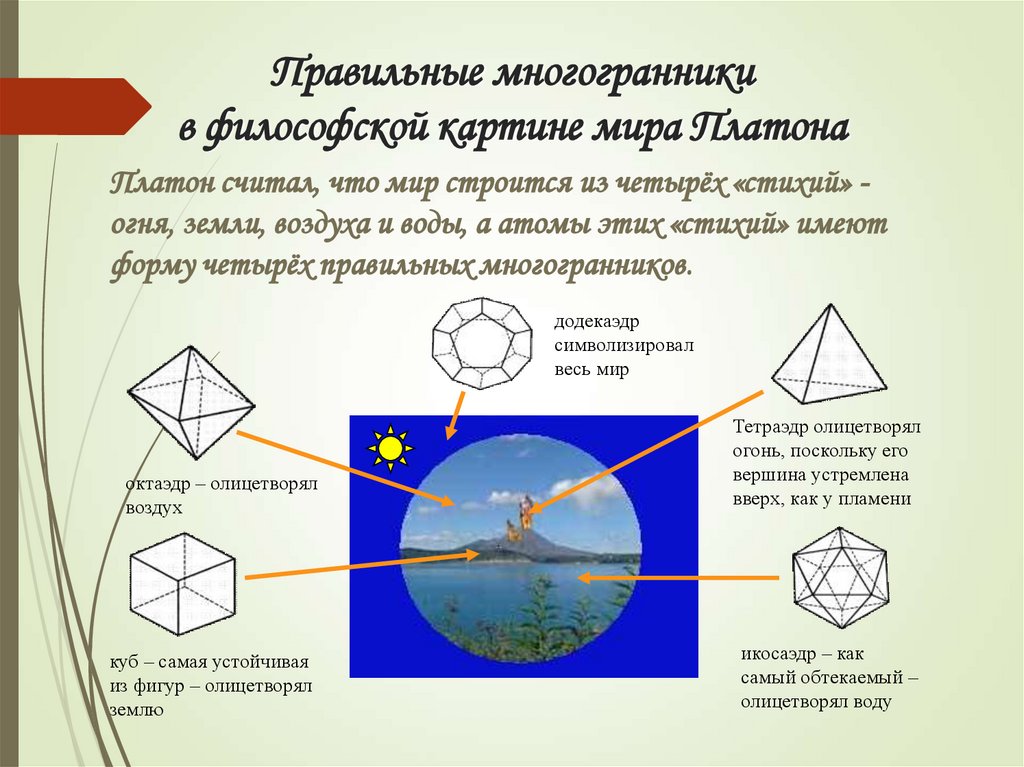
Платон считал, что мир строится из четырёх «стихий» огня, земли, воздуха и воды, а атомы этих «стихий» имеют
форму четырёх правильных многогранников.
додекаэдр
символизировал
весь мир
октаэдр – олицетворял
воздух
Тетраэдр олицетворял
огонь, поскольку его
вершина устремлена
вверх, как у пламени
куб – самая устойчивая
из фигур – олицетворял
землю
икосаэдр – как
самый обтекаемый –
олицетворял воду

14.

Заполните таблицу № 2
Число
Правильный
многогранник
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
граней и вершин
(Г + В)
рёбер
(Р)

15.

Таблица № 2
Число
Правильный
многогранник
граней и вершин
(Г + В)
рёбер
(Р)
Тетраэдр
4 + 4 = 8
6
Куб
6 + 8 = 14
12
Октаэдр
8 + 6 = 14
12
Додекаэдр
12 + 20 = 32
30
Икосаэдр
20 + 12 = 32
30

16.

Формула Эйлера
Сумма числа граней и вершин любого многогранника
равна числу рёбер, увеличенному на 2.
Г+В=Р+2
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г+В Р=2

17. Задачи

1. Ребро икосаэдра равно 4 см.
Найдите площадь поверхности этого
многогранника.
2. Площадь поверхности октаэдра
равна 72 3дм 2 Найдите ребро
данного многогранника.
3. Найдите площадь и объём
гексаэдра с ребром 5 см.