Похожие презентации:
Логические основы компьютера
1. Логические основы компьютера
1Логические
основы
компьютера
§ 21. Упрощение логических
выражений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
2. Упрощение логических выражений
Логические основы компьютеров, 10 класс2
Упрощение логических выражений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
3. Упрощение логических выражений
Логические основы компьютеров, 10 класс3
Упрощение логических выражений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
4. Логические основы компьютеров
4Логические
основы
компьютеров
§ 22. Синтез логических
выражений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
5. Определения
Логические основы компьютеров, 10 класс5
Определения
Если логическая функция выражена через
дизъюнкцию, конъюнкцию и отрицание переменных,
то такая форма представления называется
нормальной.
Среди нормальных форм выделяют такие, в которых
функции записываются единственным образом.
Их называют совершенными.
Формулу называют элементарной конъюнкцией,
если она является конъюнкцией одной или нескольких
переменных, взятых с отрицанием или без отрицания.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
6. Определения
Логические основы компьютеров, 10 класс6
Определения
Формула называется дизъюнктивной нормальной
формой (ДНФ), если она является дизъюнкцией
неповторяющихся элементарных конъюнкций.
Формула называется совершенной дизъюнктивной
нормальной формой (СДНФ), если:
1) она является ДНФ, в которой каждая элементарная
конъюнкция есть конъюнкция всех переменных,
причем на i-м месте стоит либо i-я переменная, либо
ее отрицание.
2) все элементарные конъюнкции в такой ДНФ
попарно различны.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
7. Синтез логических выражений (СДНФ)
Логические основы компьютеров, 10 класс7
Синтез логических выражений (СДНФ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 1.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат.
распределительный
X A B A B A B A (B B) A B
A A B ( A A) ( A B) A B
исключения
третьего
распределительный
К.Ю. Поляков, Е.А. Ерёмин, 2013
исключения
третьего
http://kpolyakov.spb.ru
8. Синтез логических выражений (СКНФ)
Логические основы компьютеров, 10 класс9
Синтез логических выражений (СКНФ)
A B
X
0
0
1
1
0
1
0
1
0
1
0
1
A B
A B
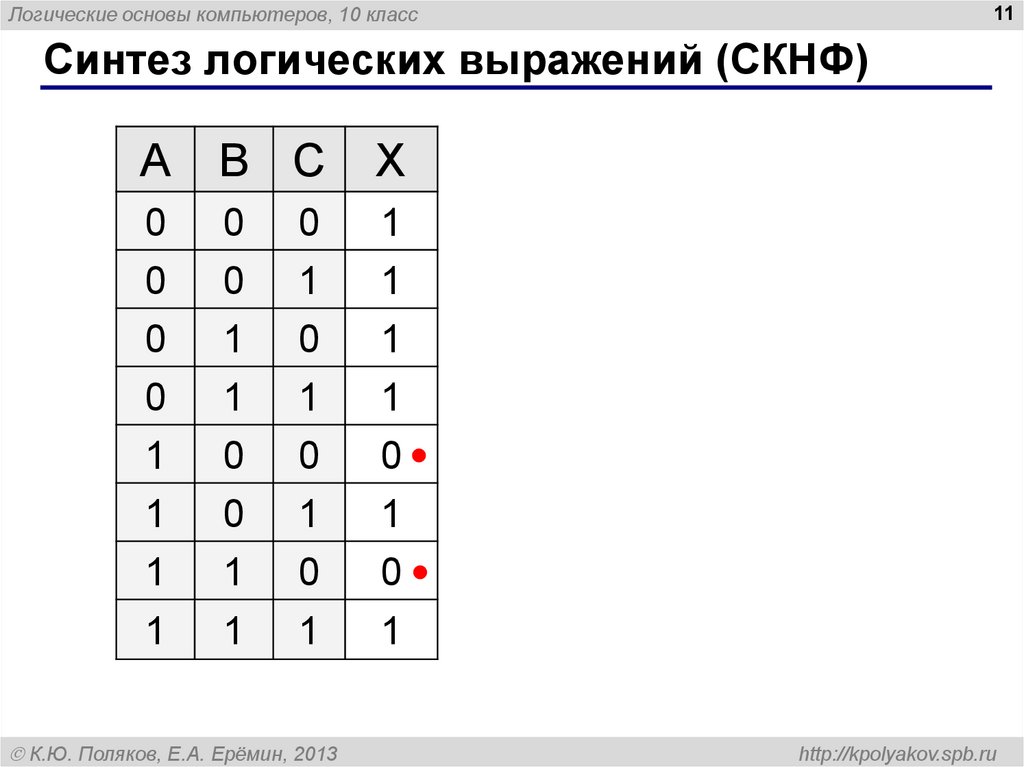
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое ложно
только для этой строки.
Шаг 3. Перемножить эти
выражения и упростить
результат.
X (A B) ( A B) A A B A A B B B
B (A A) B B
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
9. Синтез логических выражений (СКНФ)
Логические основы компьютеров, 10 класс10
Синтез логических выражений (СДНФ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
X A B C A B C
A B C
A B C
A B C
A B C
A B C
A B C
A B C A B C
A B C A B C
A B ( C C)
A B ( C C)
A C ( B B)
A B A B A C
A (B B) A C
A A C
(A A) (A C) A C
http://kpolyakov.spb.ru
10. Синтез логических выражений (СДНФ)
Логические основы компьютеров, 10 класс11
Синтез логических выражений (СКНФ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
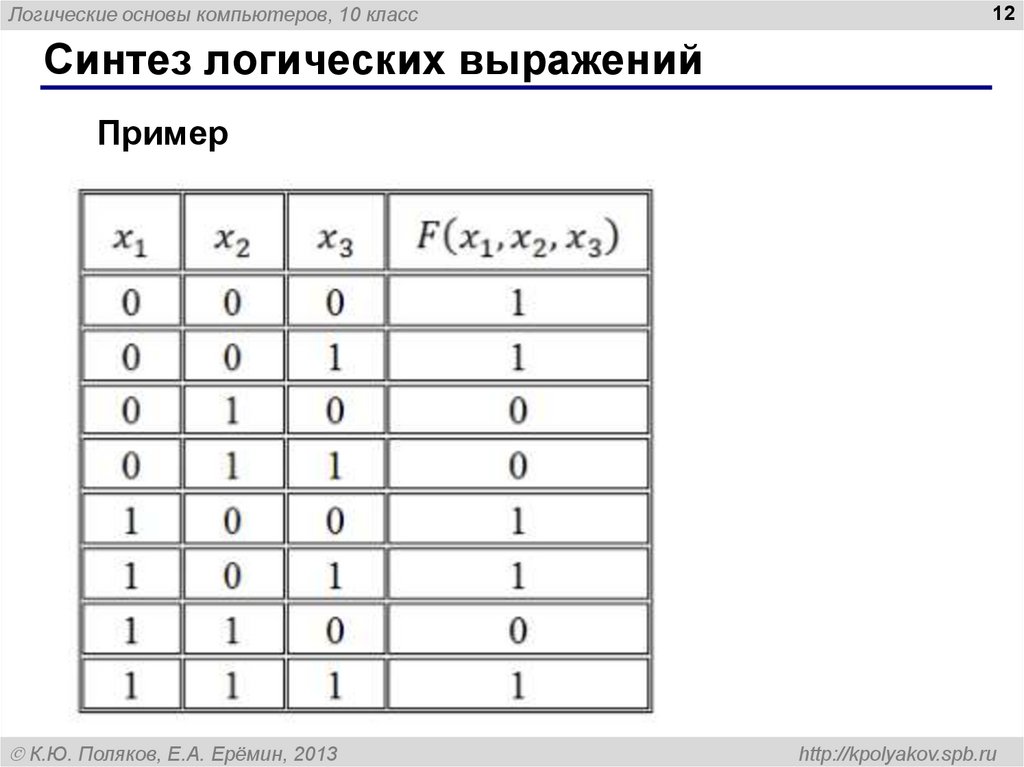
11. Синтез логических выражений (СКНФ)
Логические основы компьютеров, 10 класс12
Синтез логических выражений
Пример
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru









 Информатика
Информатика








