Система подготовки к ЕГЭ по информатике (на примере задания №26)

1.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №44
ГОРОДА СУРГУТА
МАСТЕР-КЛАСС
СИСТЕМА ПОДГОТОВКИ К ЕГЭ ПО ИНФОРМАТИКЕ
(НА ПРИМЕРЕ ЗАДАНИЯ №26)
учитель информатики высшей
квалификационной категории,
Петрова Татьяна Валентиновна,
учитель информатики первой
квалификационной категории
Андреева Оксана Евгеньевна
Сургут, 2020г.

2.

Сегодня уже не имеет смысла рассуждать о
плюсах и минусах экзамена в форме ЕГЭ, надо принять
это как данность. Значение ЕГЭ трудно переоценить.
Низкая оценка ЕГЭ может повлиять на всю дальнейшую
судьбу выпускника.
Задумываясь над секретами успешной подготовки
к сдаче экзамена на государственной итоговой
аттестации, каждый учитель старается разработать свою
стратегию, зависящую от специфики предмета.
Эффективность подготовки к ЕГЭ зависит от
множества факторов, но самое главное – это мотивация.
Эффективность подготовки и степень мотивации
готовящегося находятся в прямой зависимости.

3.

Теперь нужно определиться с критериями, по которым
мы будем оценивать эффективность подготовки. Самый
главный критерий – это балл на ЕГЭ и поступление в вуз.
Немаловажным мы считаем начальный уровень подготовки,
то есть тот уровень, с которого УЧЕНИК НАЧИНАЕТ
ПОДГОТОВКУ. Третий критерий – это скорость усвоения
материала, то есть способности ребёнка, который решил
сдать ЕГЭ. У каждого свой темп, свои пробелы в знаниях и
нужно реалистично их оценивать.
КРИТЕРИИ
ЭФФЕКТИВНОСТИ
ПОДГОТОВКИ
КОНЕЧНЫЙ
РЕЗУЛЬТАТ
СТАРТОВЫЕ
ПОЗИЦИИ
СКОРОСТЬ

4.

Система подготовки к ЕГЭ
ЕГЭ 2020
ИНФОРМАТИКА
ДОПОЛНИТЕЛЬНЫЕ
ШКОЛЬНЫЕ ЗАНЯТИЯ
САМОСТОЯТЕЛЬНАЯ
ПОДГОТОВКА
ДИСТАНЦИОННАЯ
ПОДГОТОВКА
ЗАНЯТИЯ С
КВАЛИФИЦИРОВАННЫМ
РЕПЕТИТОРОМ
СЕКРЕТЫ
УСПЕШНОЙ
ПОДГОТОВКИ
Я УЧИТЕЛЬ
СТУПЕНЬКИ ИНТЕЛЛЕКТА
ПРИСТАЛЬНОГО ВЗГЛЯДА
ТРЕНИРОВКА
ОПЫТ УЧИТЕЛЕЙ, НАКОПЛЕННЫЙ НА ПРАКТИКЕ

5.

Задание 26. Умение построить
дерево игры по заданному
алгоритму и обосновать
выигрышную стратегию

6.

Спецификация КИМ для проведения
в 2020 году ЕГЭ по информатике и ИКТ
Элементы содержания, Цепочки (конечные
проверяемые на ЕГЭ
последовательности), деревья, списки,
графы, матрицы (массивы),
псевдослучайные последовательности
Проверяемые умения
или способы действий
Строить информационные модели
объектов, систем и процессов в виде
алгоритмов
Уровень сложности
задания
В (ВЫСОКИЙ)
Макс. балл за
выполнение задания
3
Макс. балл за
выполнение задания
30 мин (НО, МОЖНО ГОРАЗДО
МЕНЬШЕ)

7.

Указания по оцениванию
В задаче требуется выполнить три задания. Их
трудность возрастает. Количество баллов в целом
соответствует количеству выполненных заданий.
Ошибка в решении, не искажающая основного
замысла и не приведшая к неверному ответу –
например, арифметическая ошибка при вычислении
количества камней в заключительной позиции – при
оценке решения не учитывается.

8.

Содержание
1. Формализация игровой ситуации;
2. Определение выигрышной стратегии для игры
двух игроков;
3. Определение выигрышной стратегии для
произвольной ситуации

9.

Формализация игровой ситуации
• Игра - многоходовый процесс, в котором
участвуют 2 и более игроков;
• выбор (ход) игрока – делается каждом шаге
игры, из конечной альтернативы вариантов
действий

10.

Игра с полной информацией
(«крестики-нолики», шахматы)
• S0 - начальная ситуация;
• D={a,b, …} - множество альтернатив на каждом
шаге постоянное;
• Si – новая ситуация (после сделанных ходов всеми
игроками);
• Sn - конечная ситуация;
• S0 Sn - траектория игрока или его стратегией.

11.

Выигрышная стратегия
В простых играх, у которых исходная
ситуация
описывается
малым
количеством
вариаций, количество игроков невелико (2 или 3
игрока), и количество альтернатив действий так же
невелик - все множество стратегий игроков можно
отобразить графом (обычно графом типа «дерево»).

12.

Выигрышная позиция
Если у игрока имеется четкая стратегия,
которая однозначно приводит его из некоторой
позиции (Si) к выигрышу, то говорят, что игрок
«имеет выигрышную позицию» в позиции (Si).

13.

Определение выигрышной стратегии
для игры двух игроков
Выигрышная позиция – это такая позиция, в
которой игрок, делающий первый ход, обязательно
выиграет при любых действиях соперника, если не
допустит ошибки; при этом говорят, что у данного
игрока есть выигрышная стратегия – алгоритм
выбора очередного хода, позволяющий ему
выиграть;
Проигрышная позиция – это такая позиция,
при которой игрок, делающий первый ход,
проигрывает независимо от выбора очередного хода.

14.

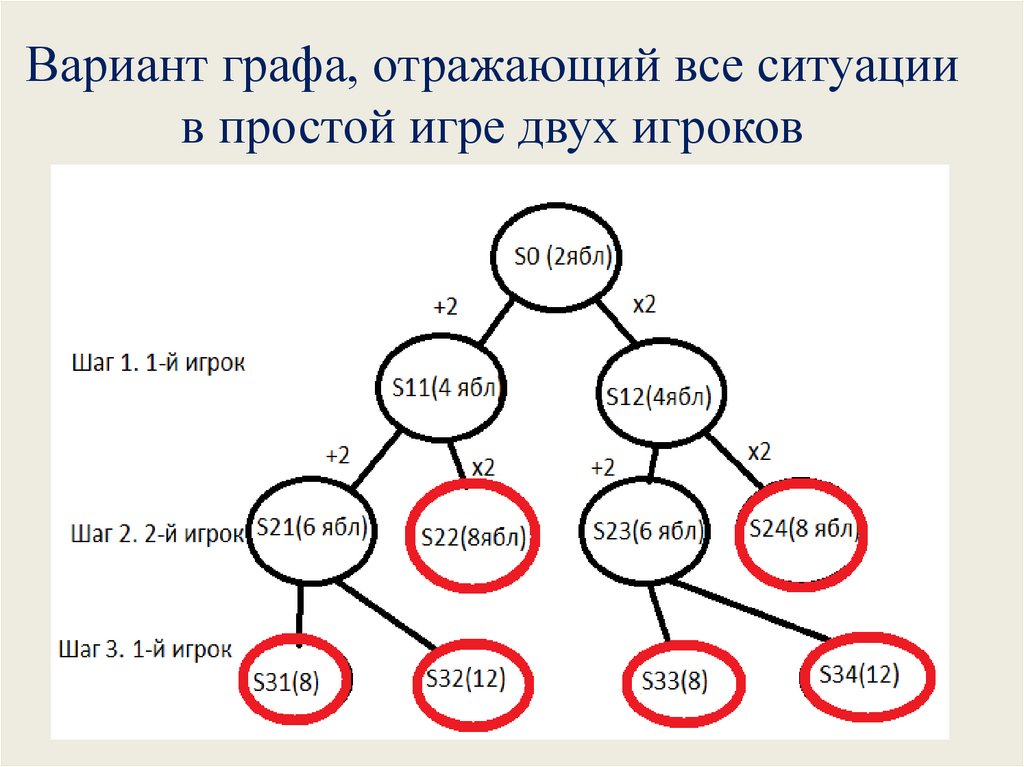
Вариант графа, отражающий все ситуации
в простой игре двух игроков

15.

Граф отображающий все множество
стратегий в игре
Ответ: Выигрывает первый игрок. Своим первым ходом он
должен добавить 2 камня в первую кучу.

16.

Вариант
таблицы,
отражающий
все ситуации в
простой игре
двух игроков

17.

Примечание для эксперта. Дерево всех партий может
быть изображено любым способом. Важно, чтобы
множество полных путей в графе (таблице)
находилось во взаимно однозначном соответствии со
множеством партий, при описании возможных
стратегий.
Не является ошибкой указание только одного
заключительного хода выигрывающего игрока в
ситуации, когда у него есть более одного
выигрышного хода.

18.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две
кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок
может добавить в одну из куч (по своему выбору) один камень или увеличить
количество камней в куче в три раза. Например, пусть в одной куче 10 камней, а
в другой 7 камней; такую позицию в игре будем обозначать (10,7) . Тогда за один
ход можно получить любую из четырёх позиций:
(11,7) – 10+1
(30,7) – 10*3
(10,7)
(10,8) – 7+1
(10,21) – 7*3
Для того чтобы делать ходы, у каждого игрока есть неограниченное количество
камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах
становится не 68 менее.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший
такую позицию, при которой в кучах будет 68 или больше камней.

19.

Запишем условие:
+1
*3
S ≥ 68
1) В первой куче 6 камней.
2) Во второй – S ( 1 ≤ S ≤ 61)
3) Петя ходит первый.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть
за один ход.
То есть, надо найти все возможные варианты (количества камней во второй
куче), при которых Петя выиграет за один ход. Очевидно, что выгоднее
использовать команду – *3.
Имеем:
6 + 3S ≥ 68
S = 21 → выигрышная позиция будет (6, 21)
ПРОВЕРЯМ:

20.

(7, 21)
(18,21)
(6,21)
(6, 22)
(6, 63) – 21*3
К = 6 + 63 = 69 / условие выполнено, игра завершена
Если S < 21, то К max = 66 / (6,20) → (6, 20*3) → S = 66
Если S > 21, то К max = 72, при позиции (6, 22); К max = 75, при позиции (2, 23) и т.д.
То есть, при 21 ≤ S ≤ 61, Петя однозначно выиграет за один ход.
Записать надо так:
Задание 1
а) Петя может выиграть при 21 ≤ S ≤ 61.
ЛИШНЕГО НИЧЕГО ПИСАТЬ НЕ НАДО!

21.

Задание 1
b) Известно, что Ваня выиграл своим первым ходом после неудачного первого хода
Пети. Укажите минимальное значение S, когда такая ситуация возможна.
То есть, S < 21, так как, исходя из п.а), если 21 ≤ S ≤ 61, то Петя выиграет первым.
Надо найти такое Smin, при котором, Петей будет создана выигрышная позиция (6, 21).
Следовательно Smin = 7.
ПРОВЕРИМ:
(6, 7) → первый возможный неудачный ход Пети, который даст возможность Ване
выиграть своим первым ходом: (6, 7*3) → (6, 21), а это выигрышная позиция (см.
п.а). Если S < 7, например 6, то максимальное значение K = 24:
(6,6) → (6, 6*3) → (6, 18).
Записать надо так:
Задание 1
b) S = 7.
ЛИШНЕГО НИЧЕГО ПИСАТЬ НЕ НАДО!

22.

Задание 2
Укажите такое значение S, при котором у Пети есть выигрышная стратегия,
причём одновременно выполняются два условия:
Петя не может выиграть за один ход.
Петя может выиграть своим вторым ходом независимо от того, как будет ходить
Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
То есть, надо найти такое значение S (количество камней во второй куче), при
котором Петя не выиграет с первого хода, но и не даст возможность Ване
выиграть его первым ходом. Причем, любой ход Вани для второго Петиного хода,
создаст выигрышную ситуацию.
S max = 20 (это число легко увидеть из решения первого задания).
(6,20) П1: (6+1,20) В1:
(7,20)
(8,20)
(8,60) → К = 68
(21,20)
(21,60) → К = 81
(7,21)
(7,60)
П2:
(7,63) → К = 70
(7,180) → К = 187
количество камней во второй куче умножает на 3
Как бы Ваня не сыграл, любая его позиция выигрышная для Пети.
Возможно, вы найдете еще значение S, которое создаст для Пети выигрышную
стратегию со второго хода. Его надо описать аналогично.

23.

Записать надо так:
Задание 2
Возможное значение S = 20. В этом случае Петя, очевидно, не может выиграть
первым ходом. Однако он может получить позицию (7,20). После хода Вани может
возникнуть одна из 4-х позиций: (8,20), (21,20), (7,21), (7,60). В каждой из этих
позиций Петя может выиграть одним ходом, утроив количество камней во второй
куче.
ВАЖНО!
Достаточно указать одно значение S и описать для него
выигрышную стратегию. Можно нарисовать дерево всех
возможных при выбранной стратегии Пети партий (и только
их).

24.

Задание 3
Укажите значение S, при котором одновременно выполняются два
условия:
• у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
• у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной
стратегии Вани (в виде рисунка или таблицы).
В узлах дерева указывайте позиции, на рёбрах рекомендуется указывать
ходы. Дерево не должно содержать партии, невозможные при реализации
выигрывающим игроком своей выигрышной стратегии. Например, полное
дерево игры не является верным ответом на это задание.

25.

Еще раз: надо найти S, причем
обязательно
учитывать условия:
у Вани есть выигрышная стратегия (первым или
вторым ходом) при любой игре Пети;
первый ход не гарантированно выигрышный.
То есть, первая стратегия может быть выигрышная,
может, нет, но вторая – однозначно должна быть
выигрышная!
Smin, при котором однозначен выигрыш со второго
хода – 20, позиция (6,20) (см. задание 2).
Следовательно рассмотрим S = 19.

26.

(8,60) → К = 68
выигрывает
В2:
(8,20) → К = 28
В2:
(7,21) → К = 28
(7,20) → К = 27 П2: (21,20) → К = 41
В1
:
(6,20) → К = 26
(6,19) П1:
В2: (21,60) → К = 81
выигрывает
(7,60) → К = 67
В2:
В1:
(7,19) → К = 26
(18,19) → К = 37
В1:
(6,57) → К = 63
(7,63) → К = 70
выигрывает
(7,180) → К = 187
выигрывает
(7,20) → К = 27П2: такая же партия
(18,57) → К = 75
выигрывает
В1:
(6,171) → К = 177
выигрывает
Возможные партии описанной стратегии Вани: с первого хода Ваня возможно выиграет, а
после второго хода Пети, Ваня выиграет гарантированно.

27.

Записать надо так:
Задание 3
Возможное значение S = 19. После первого хода Пети
возможны позиции: (7,19), (18,19), (6,20), (6,57). В позициях
(18,19) и (6,57) Ваня может выиграть первым ходом, утроив
количество камней во второй куче. Из позиций (7,19) и
(6,20) Ваня может получить позицию (7,20). Эта позиция
разобрана в п.2. Игрок, который её получил (теперь это
Ваня), выигрывает своим вторым ходом.
Кроме того, надо нарисовать дерево или
представить ситуации в виде таблицы.

28.

Литература и источники:
1. Станкевич А. Игры на графах https://ejudge.lksh.ru/archive/2014/08/A/games.pdf
2. Построение графической схемы алгоритма https://megapredmet.ru/1-3657.html
3. Основные комбинаторные ситуации
https://cyberpedia.su/16x3e61
4. https://4ege.ru/informatika/57717-zadacha-26-egepo-informatike.html
5. https://rosuchebnik.ru/material/razbor-zadaniya-26ege-2019-po-informatike-i-ikt/