Основы теории множеств. Введение. Лекция 1

1.

Лекция 1. Введение
Основы теории множеств
1

2.

Математика – наука, изучающая
пространственные формы и
количественные отношения
Основные понятия математики: число, цифра, натуральный
ряд чисел, система счисления, счетная, вычислительная,
измерительная деятельность, величина, форма,
геометрическая фигура, время, пространство.
2

3.

Немного из истории математики:
Академик Андрей Николаевич Колмогоров (1903-1987гг) выделяет 4
периода развития математики:
1. Зарождение математики (Др. Греция в IV-V вв. до н.э.);
2. Период элементарной математики (зарождение теории чисел,
алгебры, геометрии Евклида) ;
3. Математика переменных величин (в XVII веке создаются методы
оценки движения, процессов изменения величин, преобразования
геометрических фигур, дифференциальное и интегральное
исчисление, зарождение математического анализа)
4. Современная математика (XIX-XX вв., геометрия Лобачевского,
теория игр, исследование операций, финансовая математика и др.)
3

4.

Черты современной математики:
В основе построения математической теории лежит
аксиоматический метод, при котором в фундамент теории
закладываются некоторые исходные положения, называемые
аксиомами теории, а все остальные предложения
рассматриваются как логические следствия аксиом.
Основным инструментом в математических исследованиях
являются математические доказательства – строгие
логические рассуждения.
4

5.

Черты современной математики:
В математике изучаются математические модели. Это могут
быть модели реальных явлений, а также структуры для
изучения этих моделей.
Для математика важна не природа рассматриваемых
объектов, а существующие между ними отношения. Поэтому
одна модель может быть для оценки процесса роста
населения и распада радиоактивного вещества.
5

6.

В математике используется два вида умозаключений:
Дедукция – «от общего к частному», т.е. на основе общих знаний
делать выводы для конкретного случая
Индукция – «от частного к общему», то есть на основе частных случаев
делать обобщающую оценку.
**
При формулировке математических утверждений часто используются необходимые
и достаточные условия.
Если из В следует А, то А называется необходимым условием для В.
Если же из А следует В, то А называется достаточным условием для В.
Если одновременно верны утверждения «из В следует А» и «из А следует В»,
то А называется необходимым и достаточным условием для В.
6

7.

Разделы математики:
Линейная алгебра
Аналитическая геометрия
Математический анализ
в том числе Множества
Комбинаторика
Графы
Дифференциальное и Интегральное исчисление
Теория вероятностей
Математическая статистика
7

8.

Модули дисциплины:
Модуль 1 Основы дискретной математики
(множества, комбинаторика, графы)
Модуль 2- Основы теории вероятностей (случайные
события, случайные величины, предельные
теоремы)
Модуль 3 – Основы математической статистики
Модуль 4 - Основы общей теории статистики
8

9.

Цель изучения дисциплины «Специальная
математика и основы статистики»:
-формирование основных знаний, базовых
умений и практического опыта, позволяющих
применять теоретико-вероятностный и
математико-статистический инструментарий к
решению задач прикладного характера
9

10.

Задачи изучения дисциплины
сформировать знания основных дискретных понятий курса, как
важнейшего инструмента исследования, приспособленного к
задачам практики;
формулировать и излагать теоретические вопросы в общем виде,
анализировать накопившийся конкретный материал с общих
позиций, создавая основу для введения фундаментальных понятий
дискретной математики;
объяснять закономерности, возникающие при взаимодействии
большого числа случайных факторов, в создании методов сбора и
обработки статистических данных для получения научных и
практических выводов;
10

11.

Задачи изучения дисциплины (продолжение)
сформировать знания, умения и практический опыт по
формированию информационной базы статистики, в том числе
статистического наблюдения, сводки и группировки, абсолютных,
относительных и средних величин; методов сбора, анализа и
обработки данных, необходимых для решения поставленных
экономических задач; сформировать практический опыт
применения современных технических средств и
информационных технологий для решения аналитических и
исследовательских задач.
11

12.

Учебная литература: Основная
1. Балдин, К.В. Теория вероятностей и математическая статистика : учебник /
К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. – 3-е изд., стер. – Москва :
Дашков и К°, 2020. – 472 с. : ил. – Режим доступа: по подписке. – URL:
http://biblioclub.ru
2. Статистика : учебник для вузов / И. И. Елисеева [и др.] ; ответственный
редактор И. И. Елисеева. — 5-е изд., перераб. и доп. — Москва : Издательство
Юрайт, 2021. — 572 с. — (Высшее образование). — ISBN 978-5-534-10130-0. —
Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL:
https://urait.ru/bcode/47547
3. Редькин, Н.П. Дискретная математика : учебник / Н.П. Редькин. – Москва :
Физматлит, 2009. – 263 с.[Электронный ресурс]. - URL: URL:
http://biblioclub.ru/
12

13.

Учебная литература: Дополнительная
1. Анализ данных : учебник для вузов / В. С. Мхитарян [и др.] ; под редакцией В. С.
Мхитаряна. — Москва : Издательство Юрайт, 2021. — 490 с. — (Высшее образование). —
ISBN 978-5-534-00616-2. — Текст : электронный // Образовательная платформа Юрайт
[сайт]. — URL: https://urait.ru/bcode/469022
2. Черткова, Е. А. Статистика. Автоматизация обработки информации : учебное пособие
для вузов / Е. А. Черткова. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2021.
— 195 с. — (Высшее образование). — ISBN 978-5-534-01429-7. — Текст : электронный //
Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/471254
3. Яковлев, В. Б. Статистика. Расчеты в Microsoft Excel : учебное пособие для вузов / В.
Б. Яковлев. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2021. — 353 с. —
(Высшее образование). — 15 ISBN 978-5-534-01672-7. — Текст : электронный //
Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/471895
4. Гашков, С. Б. Дискретная математика: учебник и практикум для вузов / С. Б. Гашков, А.
Б. Фролов. — 3-е изд., испр. и доп. — Москва: Издательство Юрайт, 2021. — 483 с. —
(Высшее образование). — ISBN 978-5-534-11613-7. — Текст : электронный //
Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/469349
13

14.

Учебная литература: Дополнительная
5.Кремер, Н. Ш. Математический анализ. В 2-х частях. Ч.1 : учебник и практикум для вузов—
Москва : Издательство Юрайт, 2022. — 244 с. (Теория множеств - глава 14)
6. Гмурман, В. Е. Теория вероятностей и математическая статистика : учебник для вузов / В. Е.
Гмурман. — 12-е изд. — Москва : Издательство Юрайт, 2022. — 479 с. — (Высшее образование).
— ISBN 978-5-534-00211-9. — Текст : электронный // Образовательная платформа Юрайт [сайт].
— URL: https://urait.ru/bcode/488573
7. Хамидуллин Р.Я, Гулиян Б.Ш. Математика. Базовый курс: учебник- 5 изд., переб. И доп. –М.:
Университет «Синергия», 2019, 720с. ( глава 14)
8. Хамидуллин Р.Я. Теория вероятностей и математическая статистика. Учебное пособие. М.:
Университет «Синергия», 2020, 276с.
14

15.

Перечень ресурсов информационно-коммуникационной
сети «Интернет»
Наименование ресурса
Ссылка
Современная Россия. Информационноаналитический портал
http://www.nasledie.ru/
Математическая энциклопедия онлайн
https://gufo.me/dict/mathematics_encyclopedia
Математическая онлайн-библиотека
http://math.ru/
Справочники по математике
http://eqworld.ipmnet.ru/ru/library/mathematics/ha
ndbooks.htm
Теория вероятностей. Базовые термины и
понятия
http://www.mathprofi.ru/
Электронный учебник по статистике
http://www.statsoft.ru/home/textbook
Федеральная служба государственной
статистики
http://www.gks.ru/
15

16.

Вопросы лекции №1 :
1. Понятие о множествах. Виды множеств.
2. Способы отображения множеств
3. Операции на множествах, их свойства
4. Отношения над множествами
16

17.

Понятие о множествах.
Виды множеств.
17

18.

Определение
множества:
Множество – это совокупность объектов (элементов),
которые понимаются как единое целое
Синонимы множества:«семейство», «класс»,
«система», «собрание», «ансамбль», «коллекция» и
др.
18

19.

Обозначения множеств:
•Множества
обозначаются
буквами: A, B, C, …, X, ….
прописными
•Предметы (объекты), составляющие данное
множество, называют его элементами, они
обозначаются строчными буквами - а, в, с, ….
19

20.

Основатель теории множеств Георг Кантор (1845 - 1918)
нем. Georg Ferdinand Ludwig Philipp Cantor
20

21.

Основатель теории множеств немецкий математик Георг Кантор
(1845 - 1918).
"Под многообразием или множеством я понимаю вообще
все многое, которое возможно мыслить как единое, т. е.
такую совокупность определенных элементов, которая
посредством одного закона может быть соединена в одно
целое."
21

22.

Эволюция теории множеств
Георга Кантора
Теория Кантора о трансфинитных числах (т.е. бесконечные
порядковые числа) первоначально была воспринята как
нарушение многовековых традиций, заложенных ещё древними
греками и отрицающих актуальную бесконечность как
легальный математический объект. Со временем канторовская
теория множеств была поставлена на аксиоматическую основу и
стала
краеугольным
камнем
в
современном
построении
оснований
математики.
На
неё
опираются математический анализ, топология, функциональный
анализ, теория меры и многие другие разделы математики.
22

23.

Принадлежность элемента
к множеству
Записывается
Если элемент не принадлежит множеству, то запись следующая
23

24.

Условные обозначения
24

25.

25

26.

множества
Виды множеств:
По содержанию элементов (числа, буквы,
уравнения, точки, векторы, объекты
материального и нематериального мира)
По числу элементов ( конечные и
бесконечные, равные, неравные)
По упорядоченности (неупорядоченные,
упорядоченные)
Пересекающиеся и непересекающиеся
26

27.

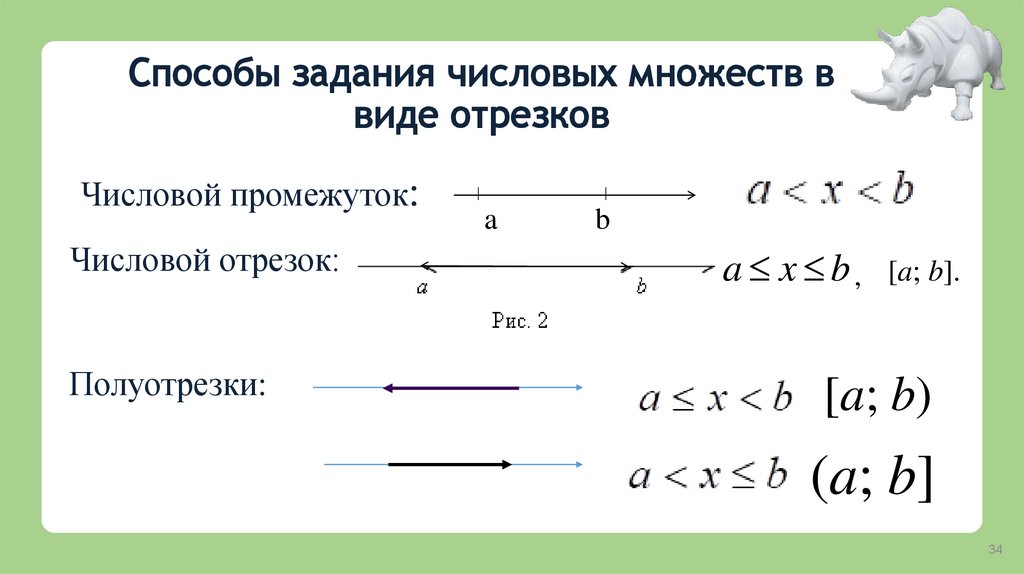
Пример множеств:
Числовые множества:
а)
множество всех натуральных чисел (N );
б)
множество всех положительных рациональных чисел (