Дробно-рациональные уравнения

1. Урок алгебры в 8 классе

«Не делай никогда того,
чего не знаешь, но научись
всему, что нужно знать».
Пифагор

2. Тема урока: Дробно-рациональные уравнения

3. Предметные знания и умения

Обогатить методологический аппарат
правомерностью использования нового
алгоритма для решения дробно-рациональных
уравнений
Учиться распознавать дробно-рациональные
уравнения
Учиться находить корни дробно-рациональных
уравнений с помощью нового алгоритма

4.

А
В
В
7 8
26 + 15 84 : 12
100 – 65 60 : 12 37 + 19
18 + 27 6 12
9 4
72 : 12 46 – 18 51 – 38
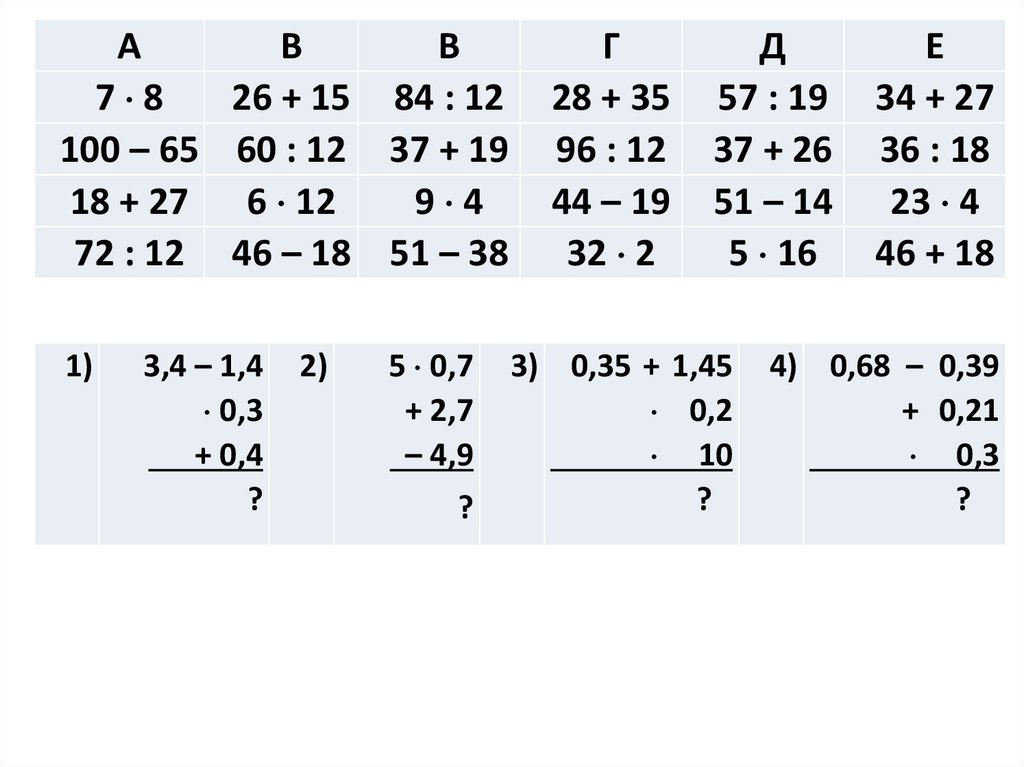
1)
3,4 – 1,4
0,3
+ 0,4
?
2)
5 0,7
+ 2,7
– 4,9
?
Г
28 + 35
96 : 12
44 – 19
32 2
Д
57 : 19
37 + 26
51 – 14
5 16
3) 0,35 + 1,45
0,2
10
?
Е
34 + 27
36 : 18
23 4
46 + 18
4) 0,68 – 0,39
+ 0,21
0,3
?

5. Мозговой штурм

1) Что такое уравнение?
2) Где здесь уравнения?
3х + 4; 2х – 5 = х; (3х+2)∙х = 0; 3х + 5х;
45 :(6 + 3) = 5?
3) Что называется корнем уравнения?
4) Что значит решить уравнение?
5) Сформулируйте условие равенства нулю
рациональной дроби.

6.

Если обе части уравнения являются рациональным
выражением, то такое уравнение называют
рациональным уравнением.
Рациональные уравнения
Целые рациональные
уравнения
2х 3
5 х;
5
2
х 6 х 8 0;
х 5 х 9
.
4
6
Дробно-рациональные
уравнения
2х 3
4 х;
5 х
х2 6х 8
0;
х 2
х 5 х 9
.
4х
6

7. Распознай уравнения

х 7
2
х 5
- дробно-рациональное уравнение
х 7
15
5
- целое рациональное уравнение
х 9 х 17 х 8
х 5
х
2
х 7 х 2
5
7
-дробно-рациональное
уравнение
2
- целое рациональное уравнение

8.

Решаем дробно-рациональное уравнение
Пример 1:
х2 6 х 8
0;
х 2
Ответ:

9.

Решаем дробно-рациональное уравнение
Пример 2:
х2
2х
х 5 х 5
Ответ:

10. Алгоритм решения дробно- рациональных уравнений

Алгоритм решения дробнорациональных уравнений
Перенести все члены уравнения влево (в
одну часть) – справа 0.
P( x)
0
Привести уравнение к виду
Q(х)
(сделать одну дробь)
P ( x) 0;
Составить и решить систему
Q ( x ) 0
Записать ответ
Примечание: не следует записывать в
ответ посторонние корни

11.

Отклонение от алгоритма может привести к приобретению
посторонних корней данного уравнения
x 2 x 3 1,
x 3
х-3
( x 2)( x 3)
1 0
x 3
x 2 3x 2 x 6 x 3
0
x 3 2
x 6x 9
0
x 3
2
( x 3)
0
x 3
x = 3 обращает знаменатель
в нуль, значит уравнение
корней не имеет.
Отклонимся от алгоритма
Сократим дробь в левой
части уравнения на (х – 3)
x 2 x 3 1,
x 3
x 2 1
x 3
При таком «способе
решения» мы получили
посторонний корень.

12. Тренировка

• № 212 (1,3,5,7), 214
Домашнее задание:
• № 213 (1,3,5), 216

13.

Пример 3:
х 1 х 3
х 2 х 2
Ответ:
0,5

14.

Пример 4:
2у 2 у 3
5
у 3 у 3
Ответ:
6; 5

15.

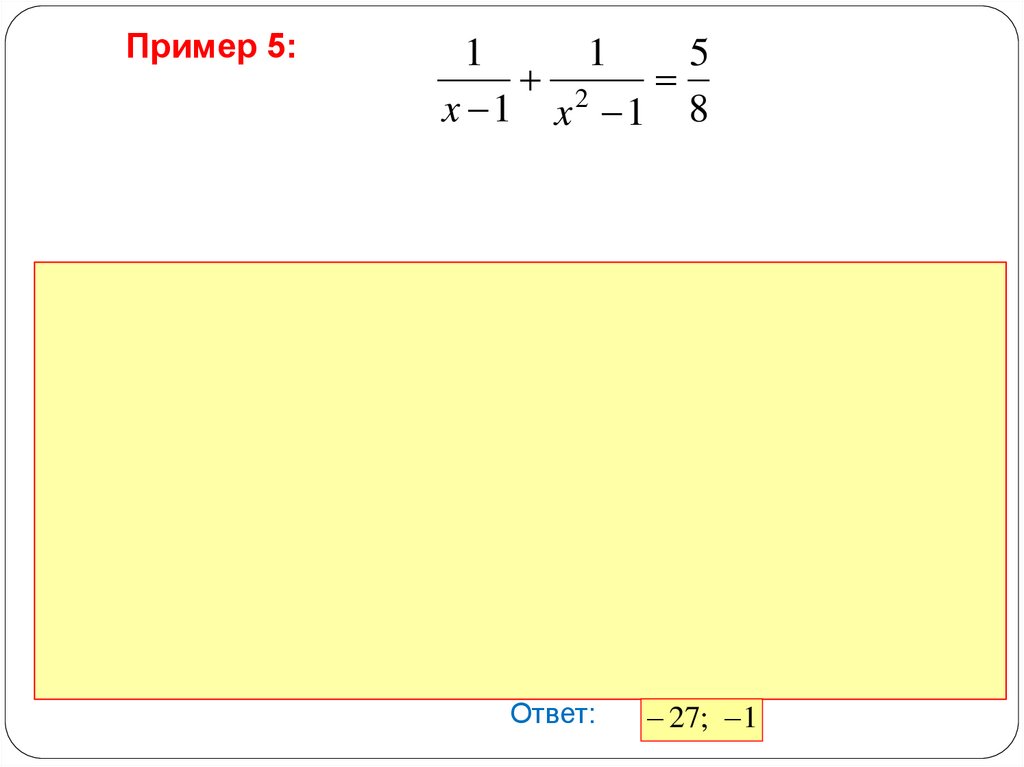
Пример 5:
1
1
5
2
x 1 x 1 8
Ответ:
27; 1