Пример выполнения типового расчета. Графы

1.

Пример выполнения типового расчета в
виде презентации

2.

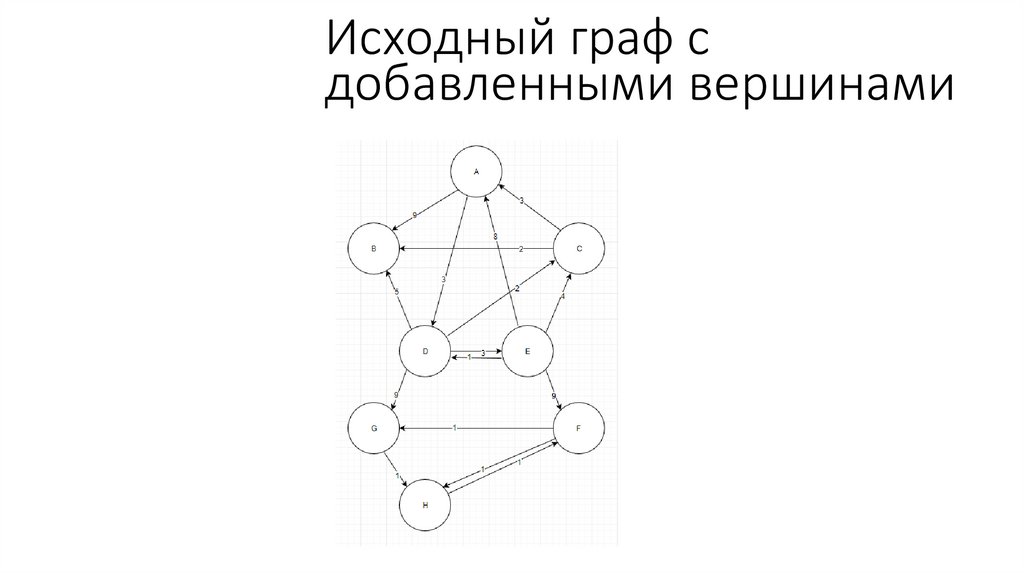
Исходный граф с
добавленными вершинами

3.

Задание 1
AB
A
B
C
D
E
F
G
H
AC
1
1
0
0
0
0
0
0
AD
1
0
1
0
0
0
0
0
Построение матрицы
инцидентности
AE
1
0
0
1
0
0
0
0
BC
1
0
0
0
1
0
0
0
BD
0
1
1
0
0
0
0
0
CD
0
1
0
1
0
0
0
0
CE
0
0
1
1
0
0
0
0
DE
0
0
1
0
1
0
0
0
DG
0
0
0
1
1
0
0
0
EF
0
0
0
1
0
0
1
0
Матрица инцидентности графа
*описание структуры графа в виде матрицы инцидентности
см в Приложении 1
FG
0
0
0
0
1
1
0
0
GH
0
0
0
0
0
1
1
0
FH
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1

4.

Задание 2
Вершина
Mark
Fin
A
0
-
B
0
-
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

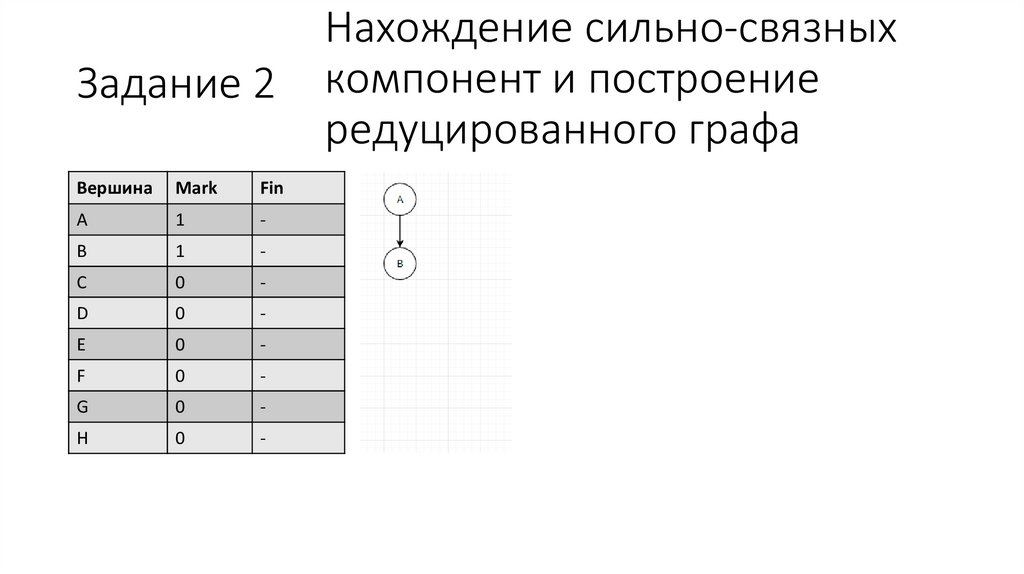
5.

Задание 2
Вершина
Mark
Fin
A
1
-
B
0
-
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

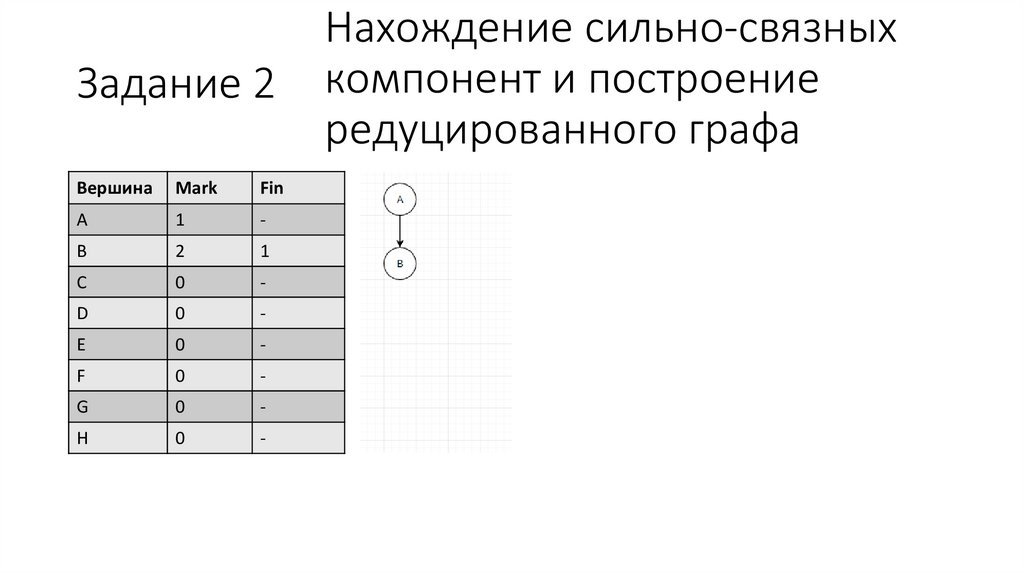
6.

Задание 2
Вершина
Mark
Fin
A
1
-
B
1
-
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

7.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

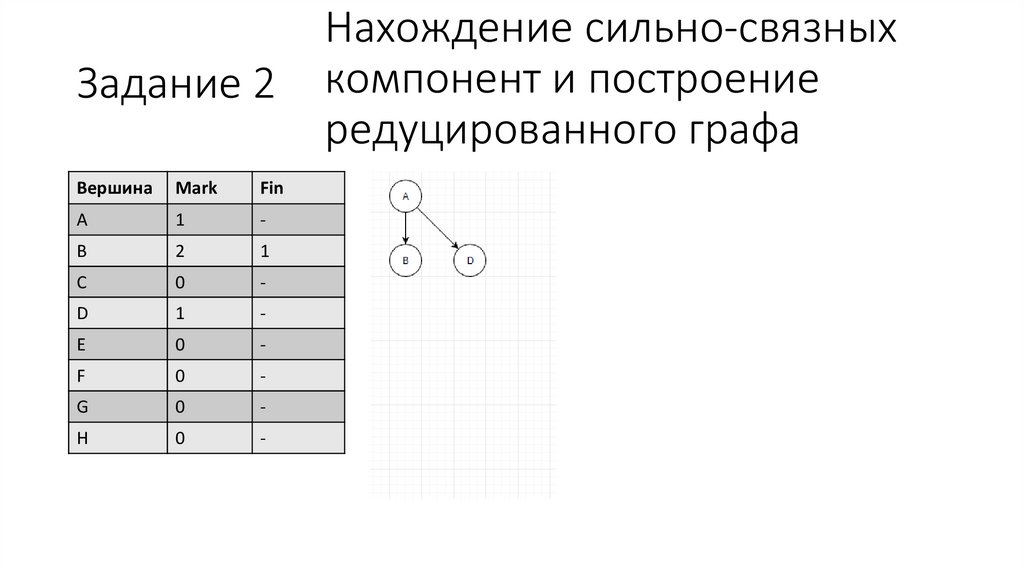
8.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
0
-
D
1
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

9.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
0
-
D
1
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа
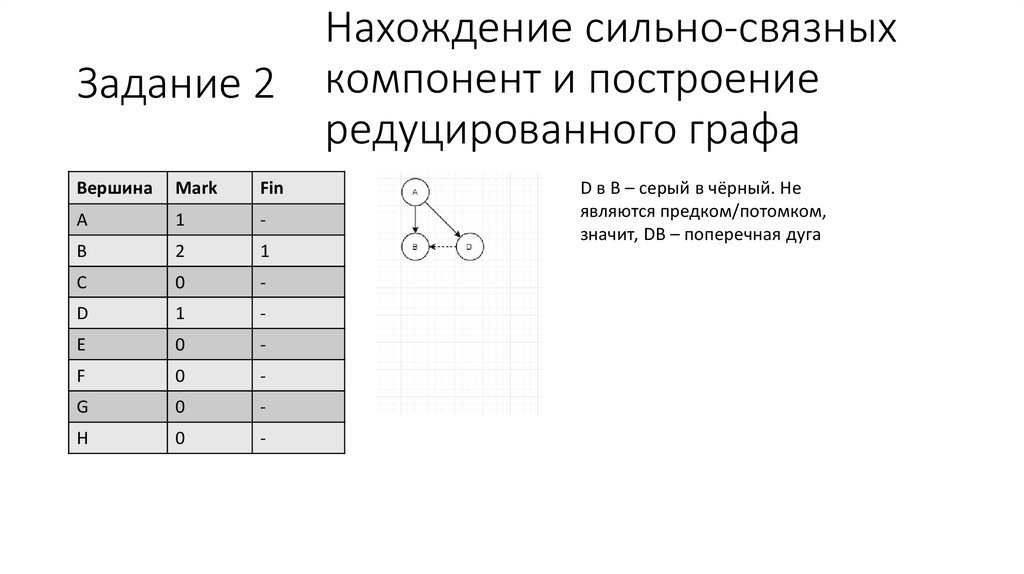
D в B – серый в чёрный. Не
являются предком/потомком,
значит, DB – поперечная дуга

10.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
1
-
D
1
-
E
0
-
F
0
-
G
0
-
H
0
-
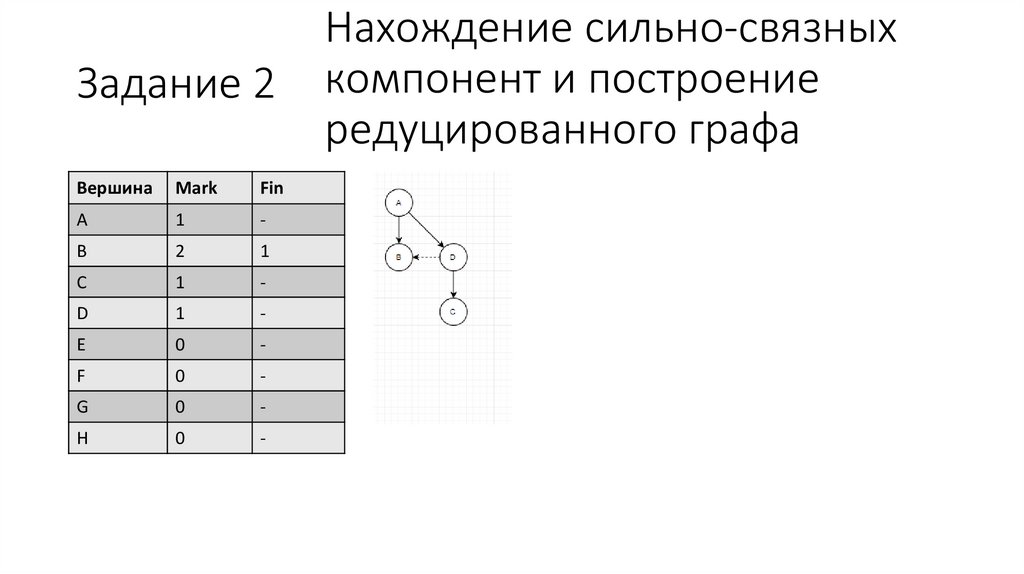
Нахождение сильно-связных
компонент и построение
редуцированного графа

11.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
1
-
D
1
-
E
0
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа
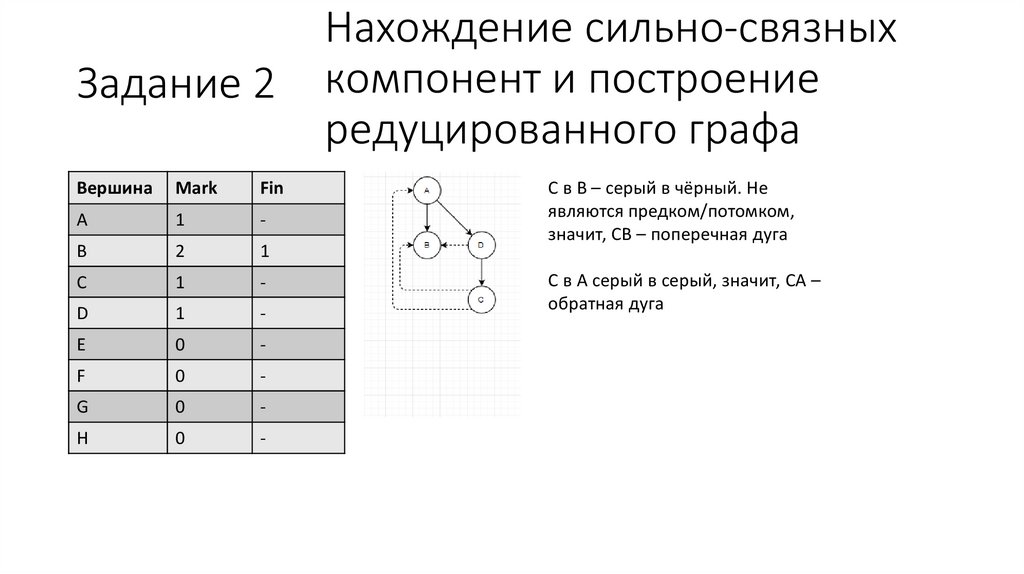
C в B – серый в чёрный. Не
являются предком/потомком,
значит, CB – поперечная дуга
C в A серый в серый, значит, CA –
обратная дуга

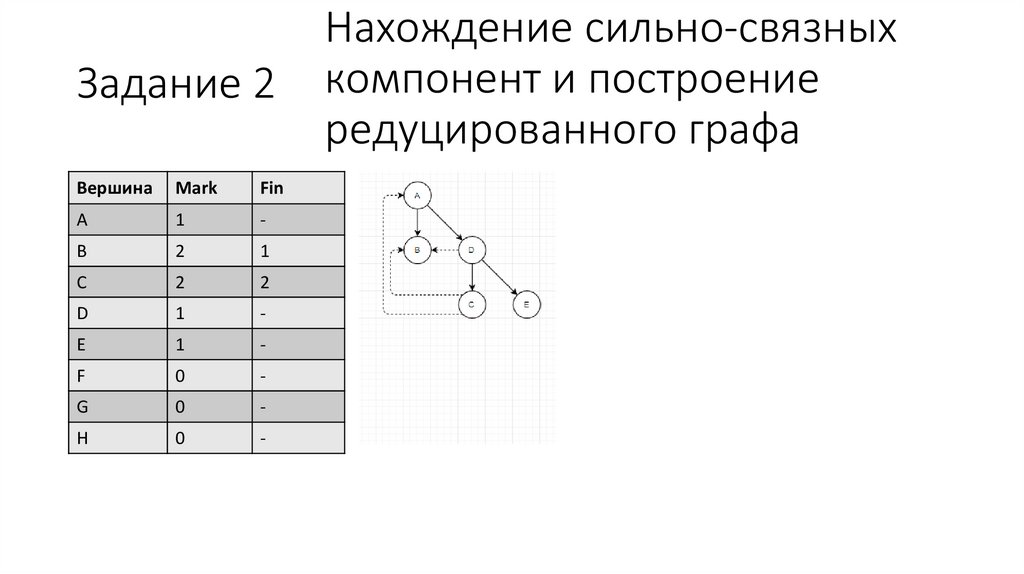
12.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
0
-
F
0
-
G
0
-
H
0
-
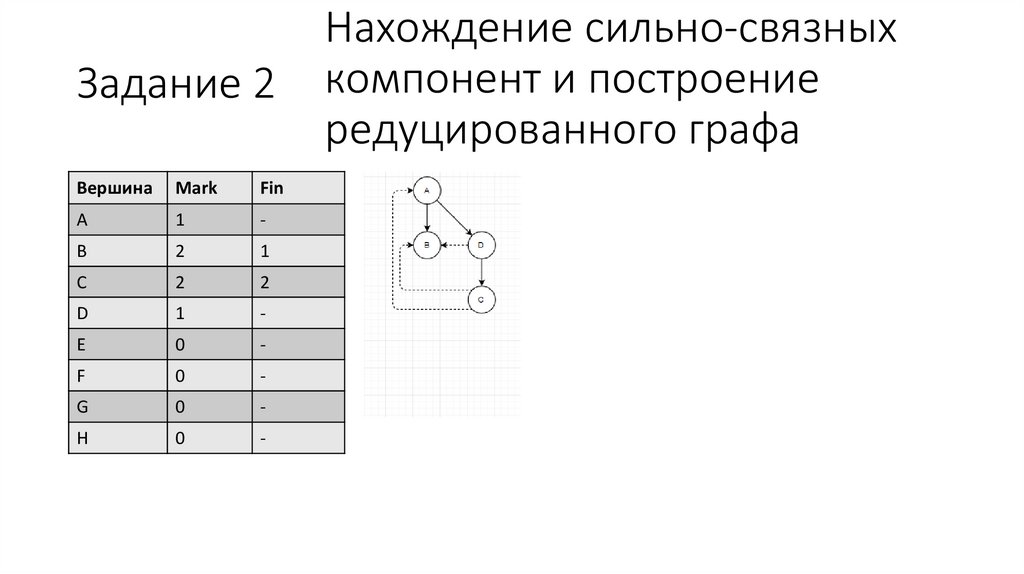
Нахождение сильно-связных
компонент и построение
редуцированного графа

13.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
0
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

14.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
0
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа
E в C – серый в чёрный. Не
являются предком/потомком,
значит, EC – поперечная дуга
E в A серый в серый, значит, EA –
обратная дуга
E в D серый в серый, значит, ED –
обратная дуга

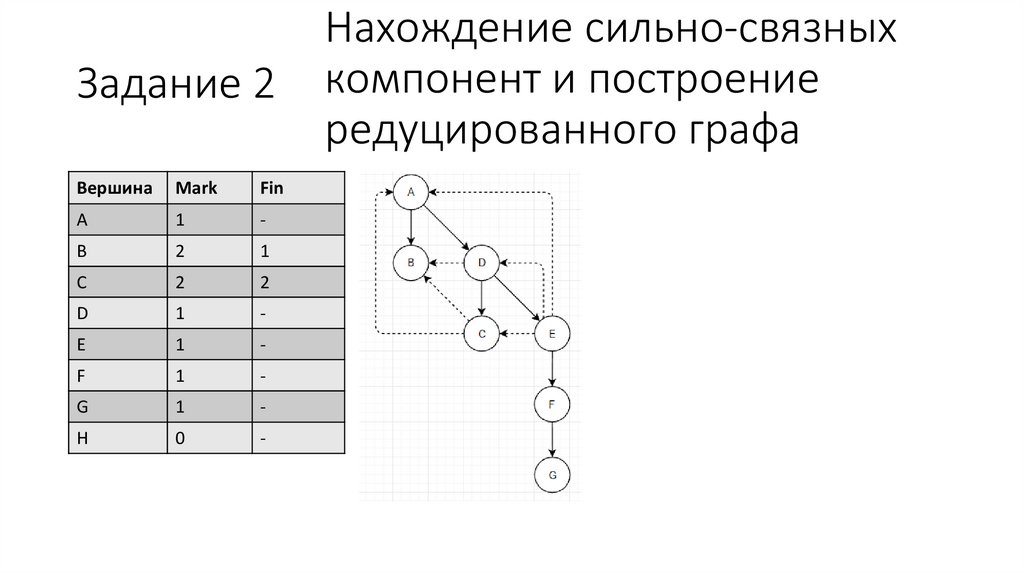
15.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
1
-
H
0
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

16.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
1
-
H
1
-
Нахождение сильно-связных
компонент и построение
редуцированного графа

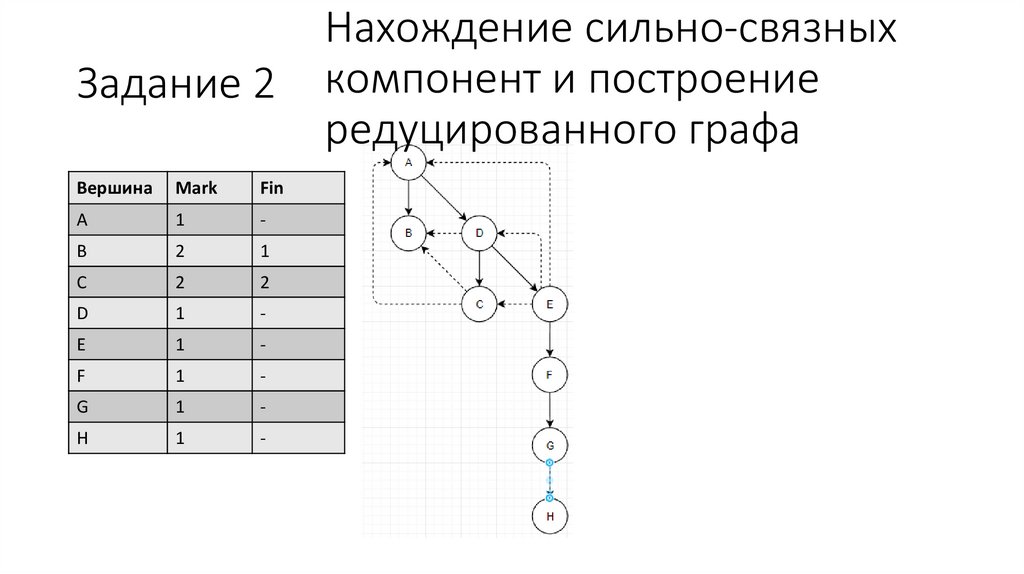
17.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
1
-
H
1
-
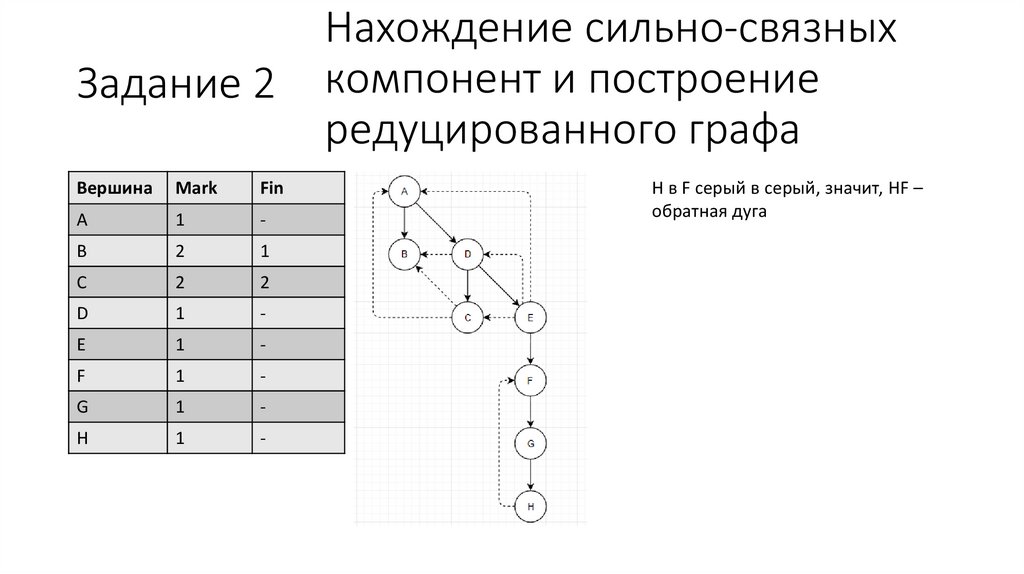
Нахождение сильно-связных
компонент и построение
редуцированного графа
H в F серый в серый, значит, HF –
обратная дуга

18.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
1
-
H
2
3
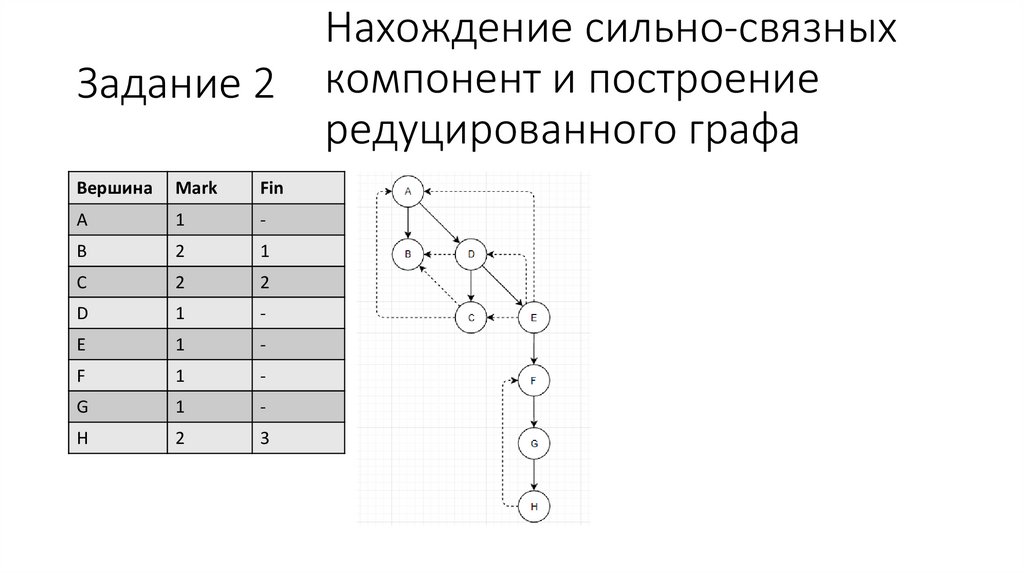
Нахождение сильно-связных
компонент и построение
редуцированного графа

19.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
2
4
H
2
3
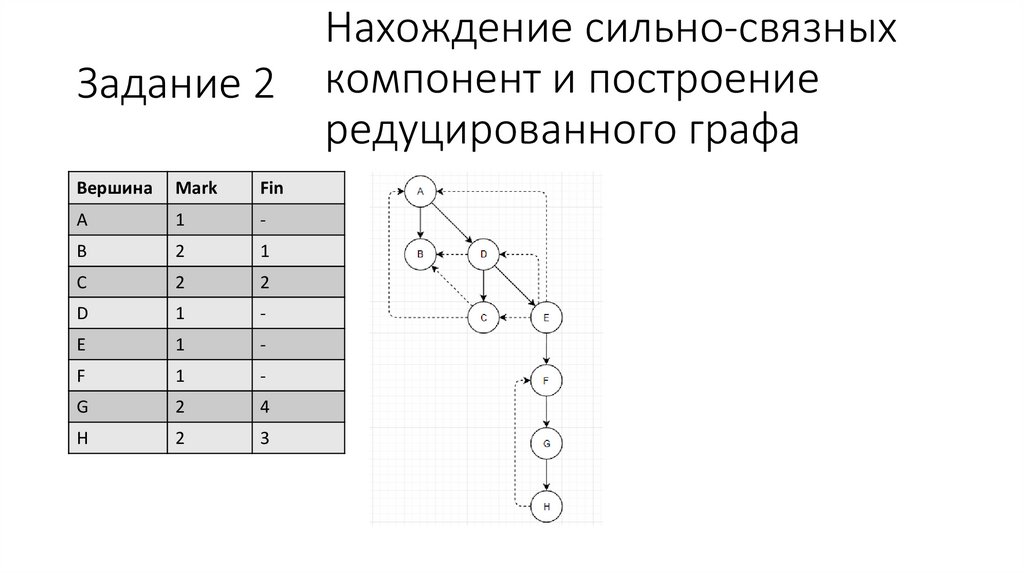
Нахождение сильно-связных
компонент и построение
редуцированного графа

20.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
1
-
G
2
4
H
2
3
Нахождение сильно-связных
компонент и построение
редуцированного графа
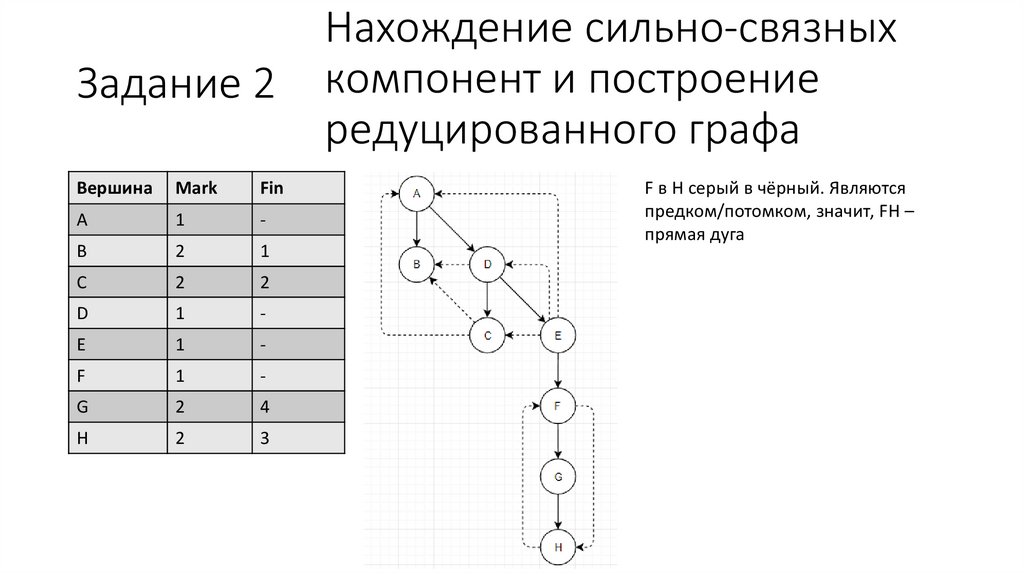
F в H серый в чёрный. Являются
предком/потомком, значит, FH –
прямая дуга

21.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
1
-
F
2
5
G
2
4
H
2
3
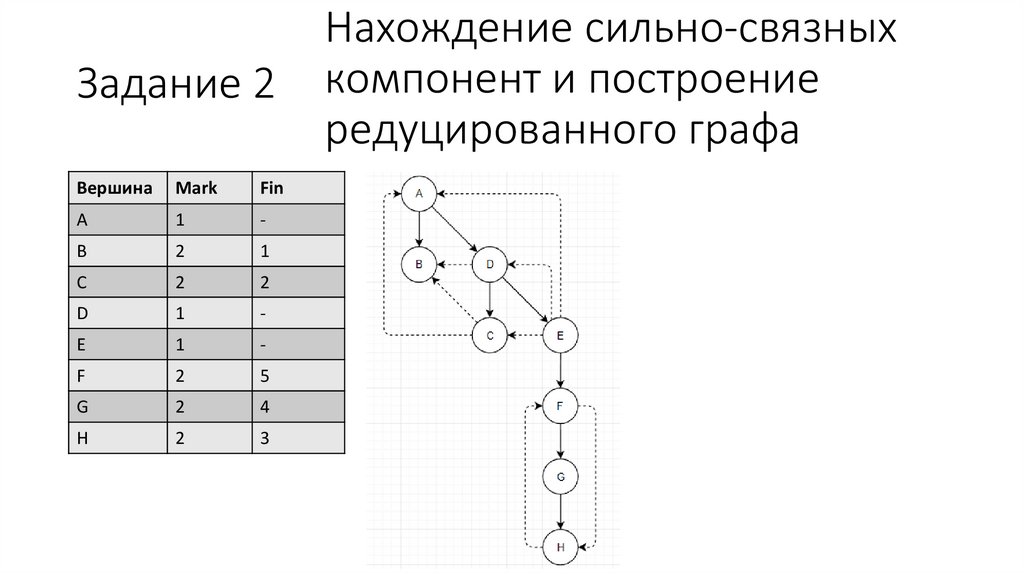
Нахождение сильно-связных
компонент и построение
редуцированного графа

22.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
1
-
E
2
6
F
2
5
G
2
4
H
2
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

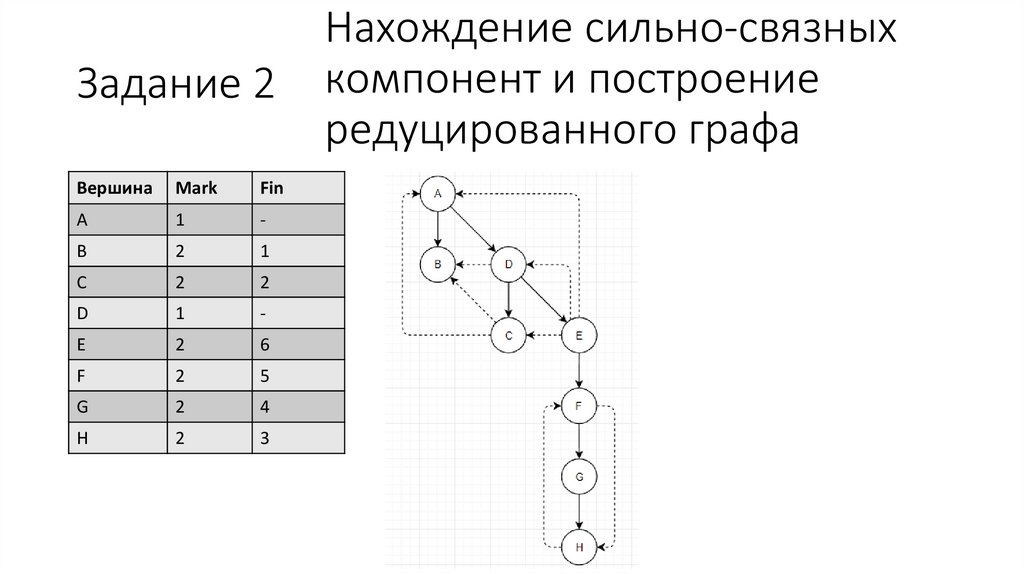
23.

Задание 2
Вершина
Mark
Fin
A
1
-
B
2
1
C
2
2
D
2
7
E
2
6
F
2
5
G
2
4
H
2
3
Нахождение сильно-связных
компонент и построение
редуцированного графа
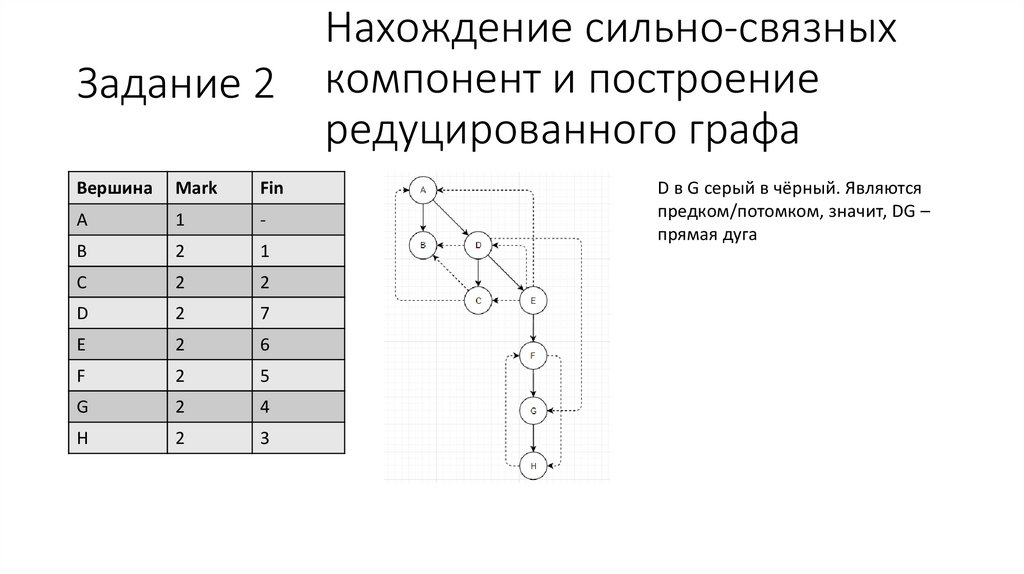
D в G серый в чёрный. Являются
предком/потомком, значит, DG –
прямая дуга

24.

Задание 2
Вершина
Mark
Fin
A
2
8
B
2
1
C
2
2
D
2
7
E
2
6
F
2
5
G
2
4
H
2
3
Нахождение сильно-связных
компонент и построение
редуцированного графа
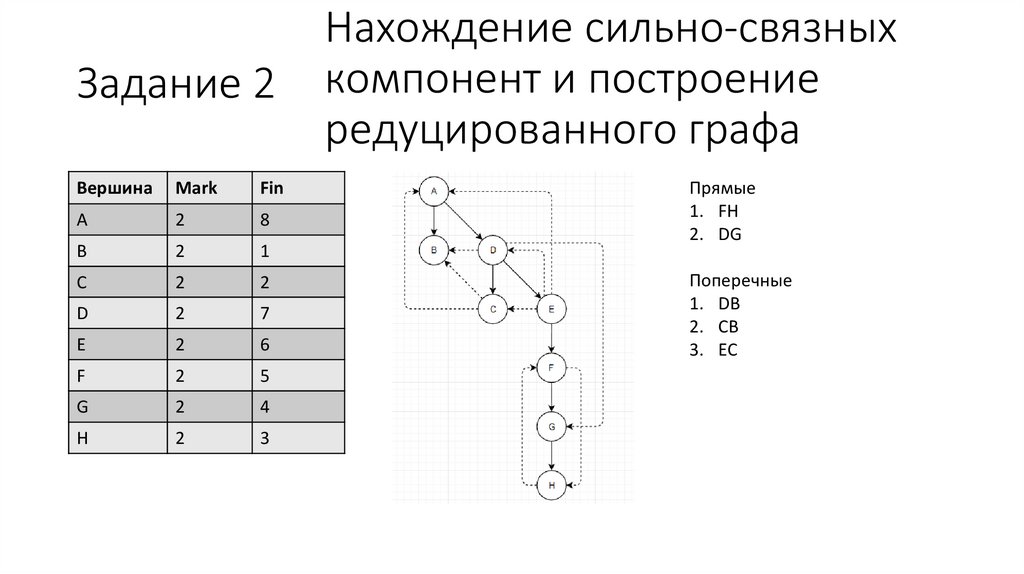
Прямые
1. FH
2. DG
Поперечные
1. DB
2. CB
3. EC

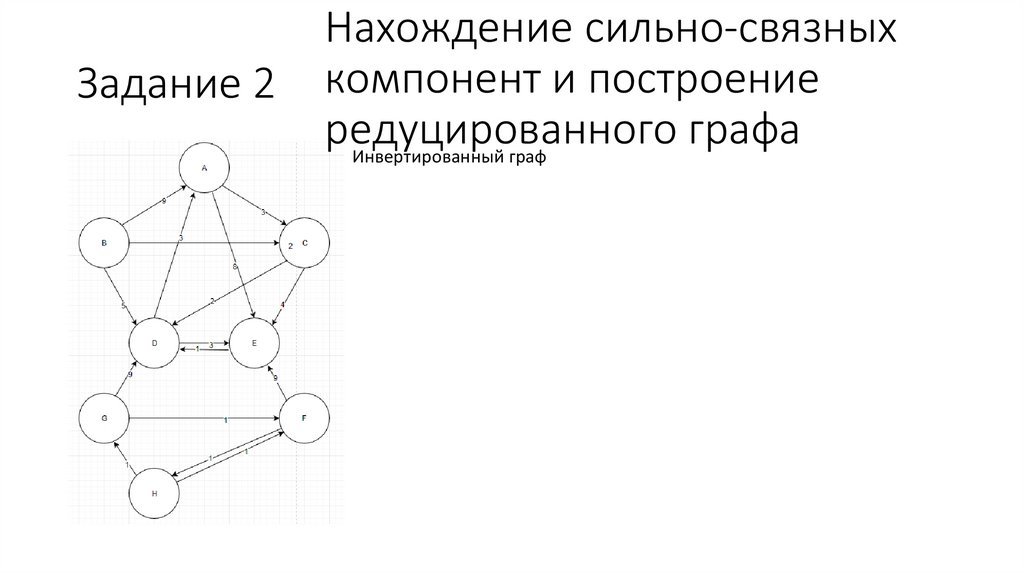
25.

Задание 2
Нахождение сильно-связных
компонент и построение
редуцированного
графа
Инвертированный граф

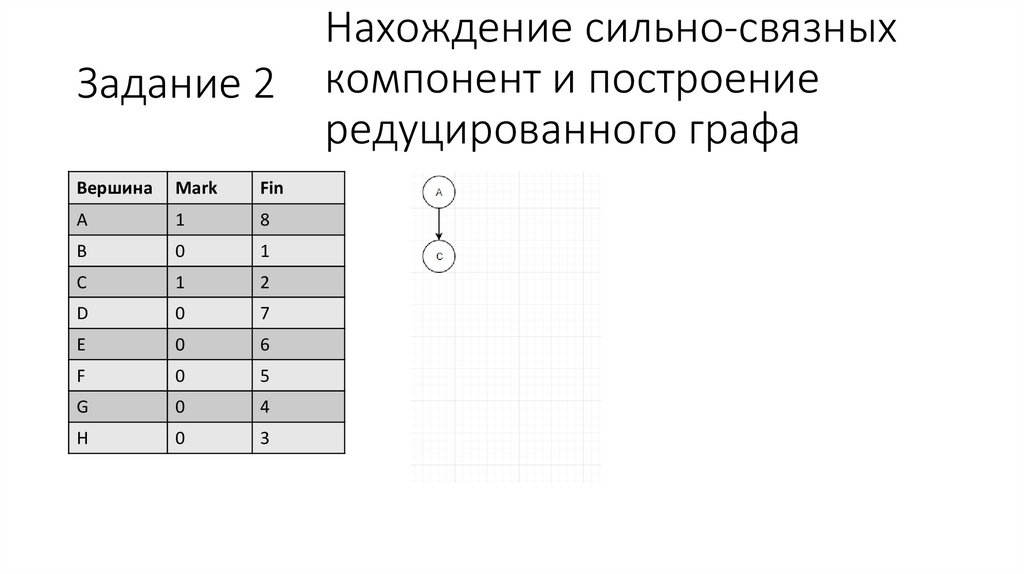
26.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
0
2
D
0
7
E
0
6
F
0
5
G
0
4
H
0
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

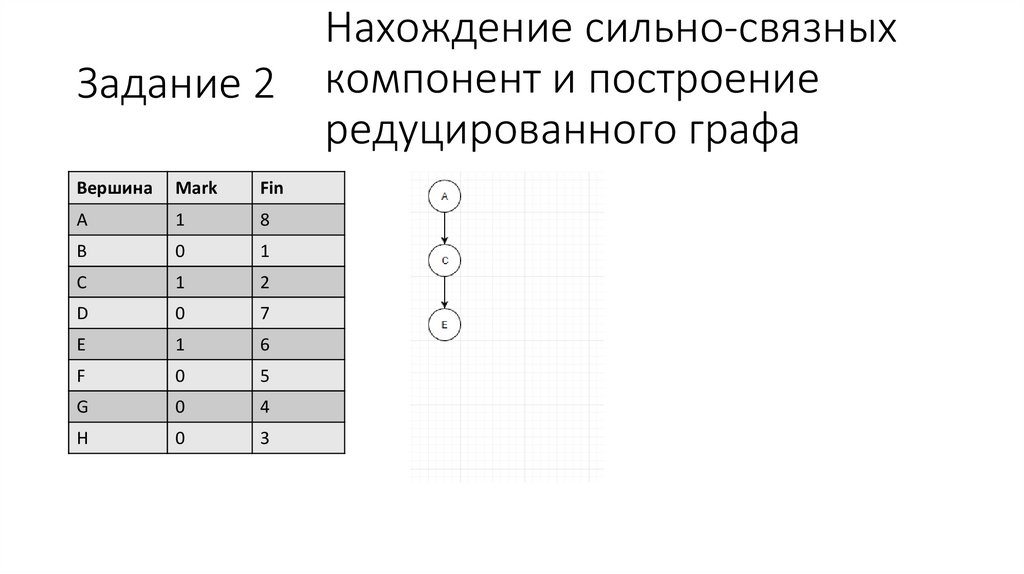
27.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
0
7
E
0
6
F
0
5
G
0
4
H
0
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

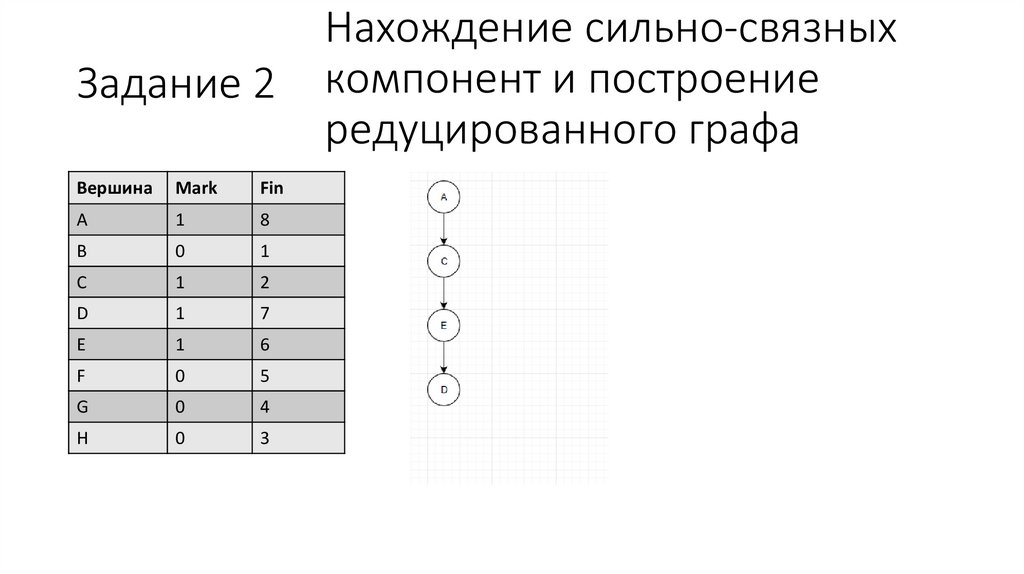
28.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
0
7
E
1
6
F
0
5
G
0
4
H
0
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

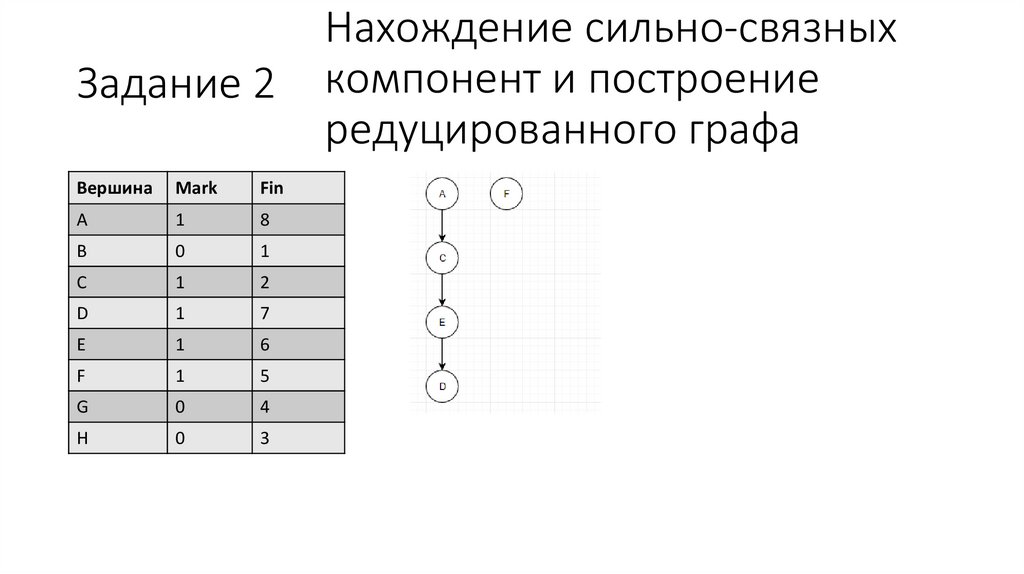
29.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
1
7
E
1
6
F
0
5
G
0
4
H
0
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

30.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
1
7
E
1
6
F
1
5
G
0
4
H
0
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

31.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
1
7
E
1
6
F
1
5
G
0
4
H
1
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

32.

Задание 2
Вершина
Mark
Fin
A
1
8
B
0
1
C
1
2
D
1
7
E
1
6
F
1
5
G
1
4
H
1
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

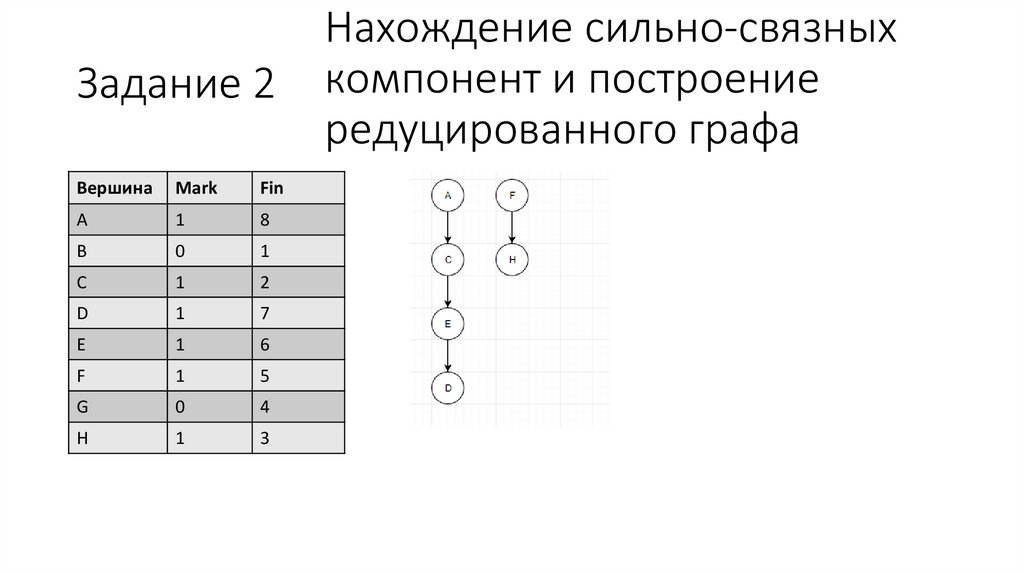
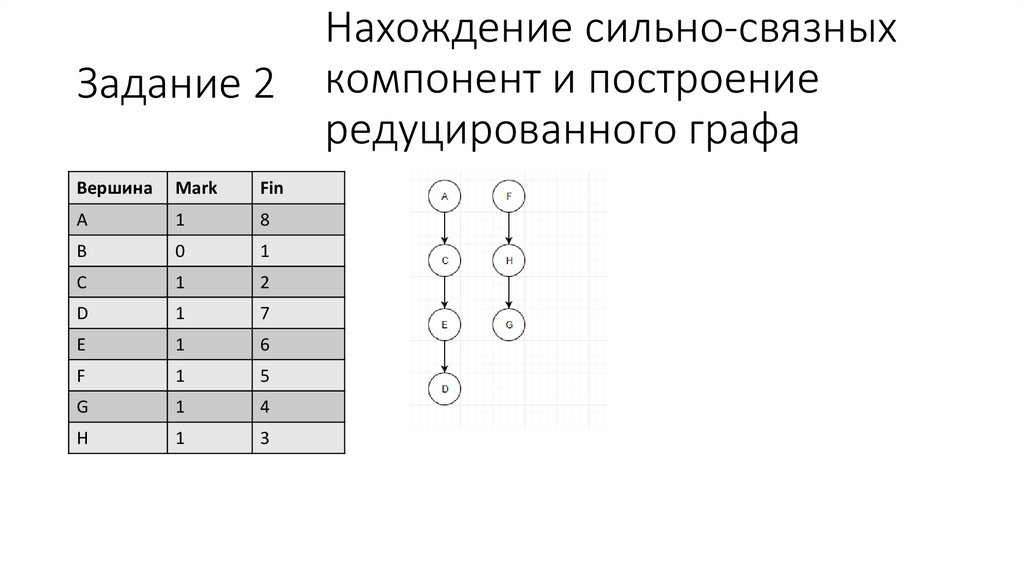
33.

Задание 2
Вершина
Mark
Fin
A
1
8
B
1
1
C
1
2
D
1
7
E
1
6
F
1
5
G
1
4
H
1
3
Нахождение сильно-связных
компонент и построение
редуцированного графа

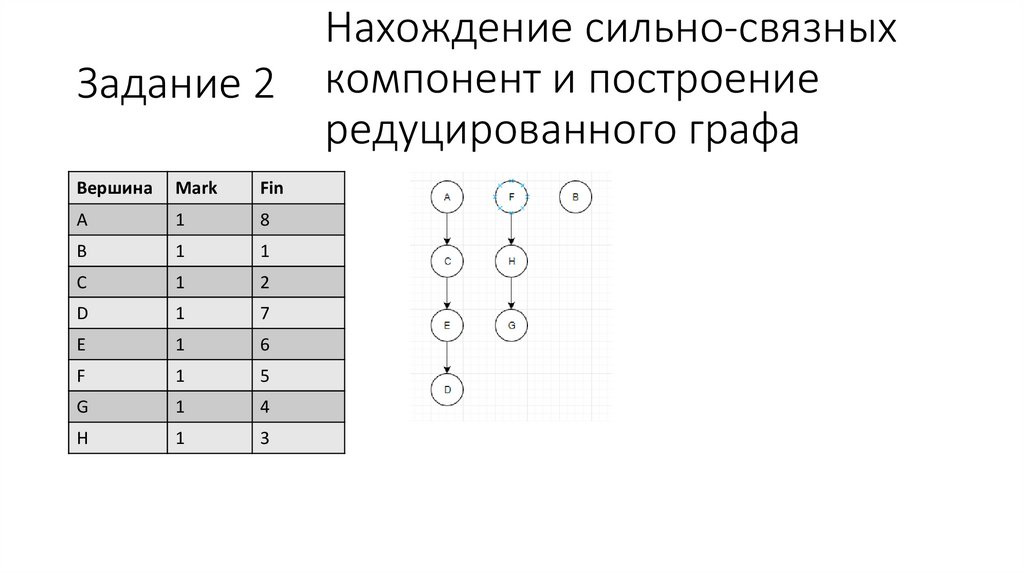
34.

Нахождение сильно-связных
Задание 3 компонент и построение
редуцированного
графа
Поиск ССК и построение редуцированного графа
Вершина
Mark
Fin
A
1
8
B
1
1
C
1
2
D
1
7
E
1
6
F
1
5
G
1
4
H
1
3
Редуцированный граф
Три ССК

35.

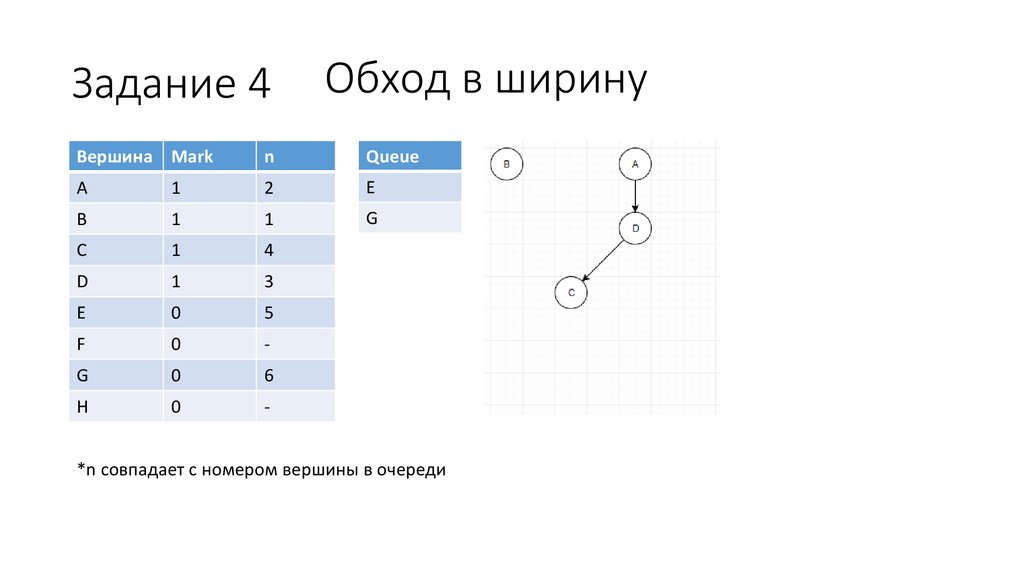
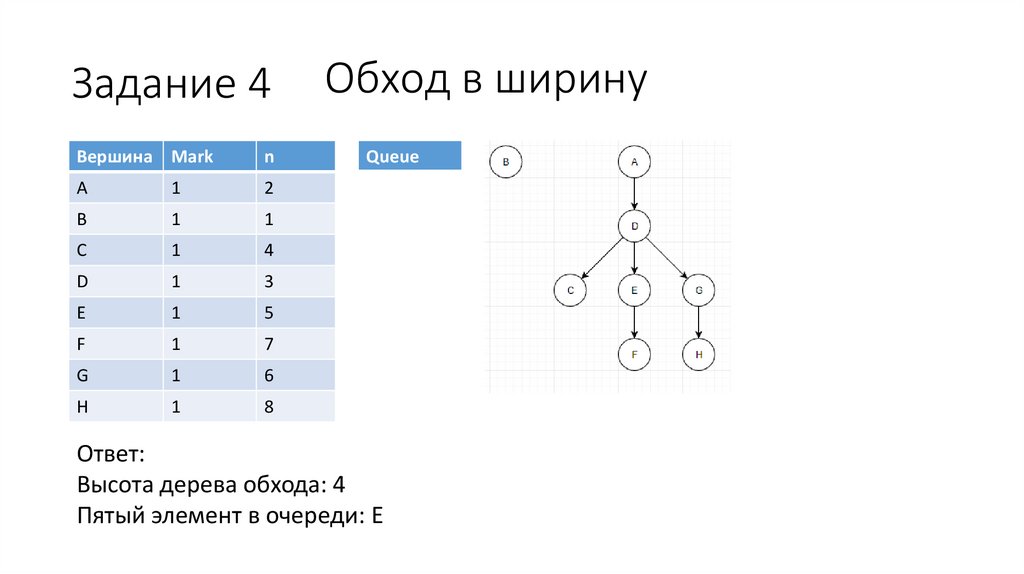
Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
0
-
B
B
0
1
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
*n совпадает с номером вершины в очереди

36.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
0
2
A
B
1
1
C
0
-
D
0
-
E
0
-
F
0
-
G
0
-
H
0
-
*n совпадает с номером вершины в очереди

37.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
D
B
1
1
C
0
-
D
0
3
E
0
-
F
0
-
G
0
-
H
0
-
*n совпадает с номером вершины в очереди

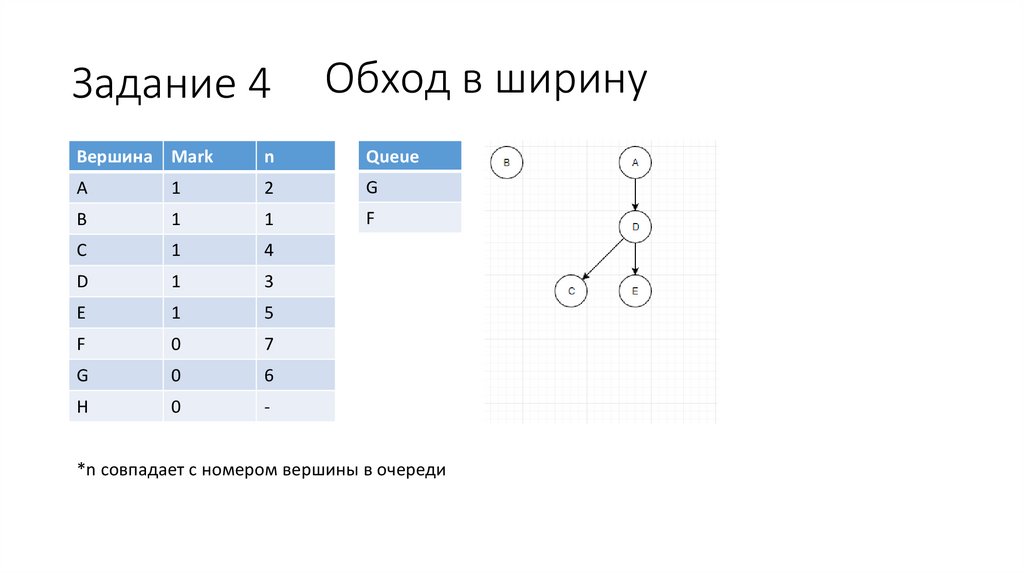
38.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
C
B
1
1
E
C
0
4
G
D
1
3
E
0
5
F
0
-
G
0
6
H
0
-
*n совпадает с номером вершины в очереди

39.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
E
B
1
1
G
C
1
4
D
1
3
E
0
5
F
0
-
G
0
6
H
0
-
*n совпадает с номером вершины в очереди

40.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
G
B
1
1
F
C
1
4
D
1
3
E
1
5
F
0
7
G
0
6
H
0
-
*n совпадает с номером вершины в очереди

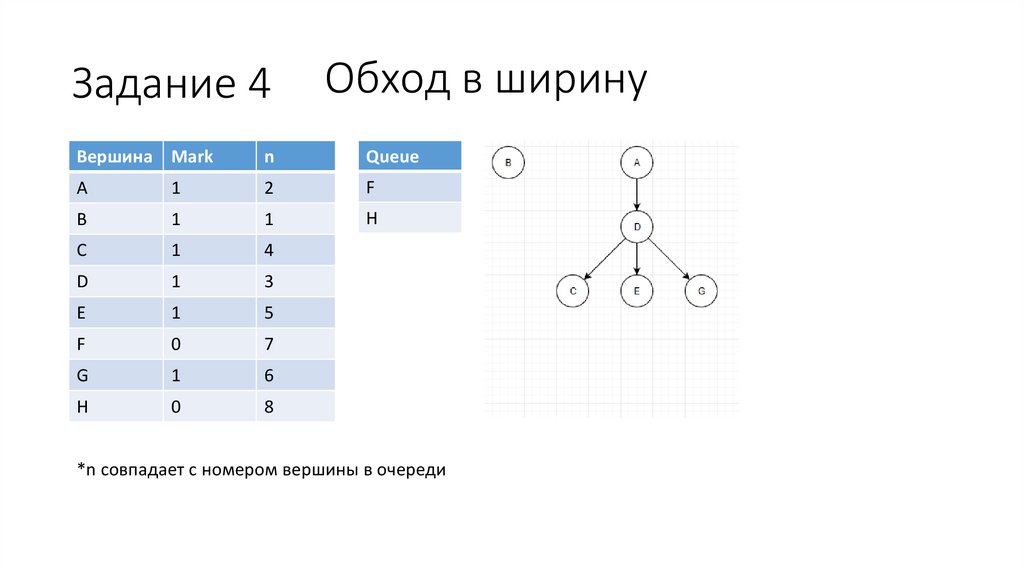
41.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
F
B
1
1
H
C
1
4
D
1
3
E
1
5
F
0
7
G
1
6
H
0
8
*n совпадает с номером вершины в очереди

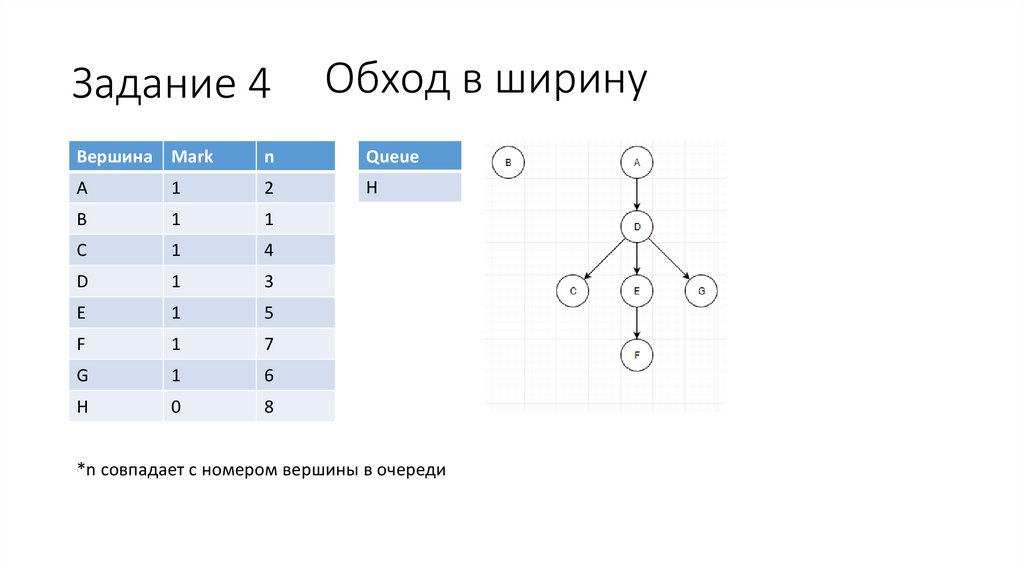
42.

Задание 4
Обход в ширину
Вершина Mark
n
Queue
A
1
2
H
B
1
1
C
1
4
D
1
3
E
1
5
F
1
7
G
1
6
H
0
8
*n совпадает с номером вершины в очереди

43.

Задание 4
Вершина Mark
n
A
1
2
B
1
1
C
1
4
D
1
3
E
1
5
F
1
7
G
1
6
H
1
8
Обход в ширину
Queue
*n совпадает с номером вершины в очереди

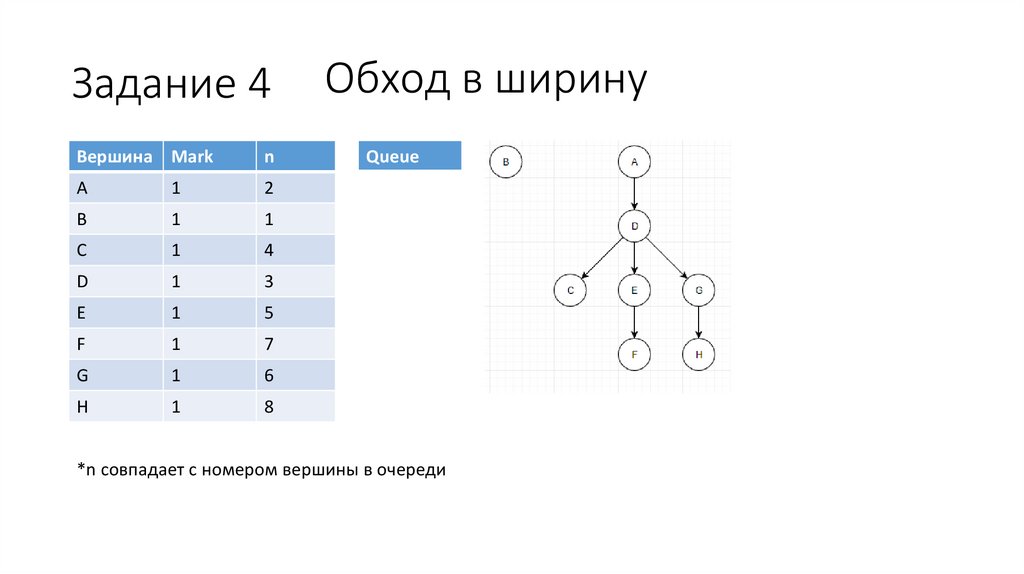
44.

Задание 4
Вершина Mark
n
A
1
2
B
1
1
C
1
4
D
1
3
E
1
5
F
1
7
G
1
6
H
1
8
Обход в ширину
Queue
Ответ:
Высота дерева обхода: 4
Пятый элемент в очереди: E

45.

Нахождение цепи/цикла
заданной длины
Задание 5
A
B
C
D
E
F
G
H
A
0
1
0
1
0
0
0
0
B
0
0
0
0
0
0
0
0
C
1
1
0
0
0
0
0
0
D
0
1
1
0
1
0
1
0
E
1
0
1
1
0
1
0
0
F
0
0
0
0
0
0
1
1
G
0
0
0
0
0
0
0
1
H
0
0
0
0
0
0
1
0
Матрица инцидентности графа G

46.

Нахождение цепи/цикла
заданной длины
Задание 5
G
F
H
G
0
0
1
F
1
0
1
H
0
1
0
Можно сразу исключить из графа вершину B,
т.к. она имеет только входящие дуги, поэтому
не может быть частью цикла.
A
C
D
E
A
0
0
1
0
C
1
0
0
0
D
0
1
0
1
E
1
1
1
0
Также можно разделить оставшийся граф на две
ССК, чтобы упростить вычисления.

47.

Нахождение цепи/цикла
заданной длины
Задание 5
G
F
H
G
0
0
1
F
1
0
1
H
0
1
0
G
F
H
G
0
1
0
F
0
1
1
H
1
0
1
A^1
G-H
F-G
F-H
H-F
A^2
G-H-F
F-H-F
F-G-H
H-F-G
H-F-H

48.

Нахождение цепи/цикла
заданной длины
Задание 5
G
F
H
G
1
0
1
F
1
1
1
H
0
1
1
G
F
H
G
0
1
1
F
1
1
2
H
1
1
1
A^3
G-H-F-G
G-H-F-H
F-H-F-G
F-G-H-F
F-H-F-H
H-F-H-F
H-F-G-H
A^4
G-H-F-H-F
G-H-F-G-H
F-G-H-F-G
F-H-F-H-F
F-H-F-G-H
F-G-H-F-H
H-F-H-F-G
H-F-G-H-F
H-F-H-F-H

49.

Нахождение цепи/цикла
заданной длины
Задание 5
G
F
H
G
1
1
1
F
1
2
2
H
1
1
2
Циклы длины 5 для ССК (G,F,H):
G-H-F-H-F-G
F-H-F-G-H-F
F-G-H-F-H-F
H-F-H-F-G-H
H-F-G-H-F-H
A^5
G-H-F-H-F-G
F-H-F-G-H-F
F-G-H-F-H-F
H-F-H-F-G-H
H-F-G-H-F-H

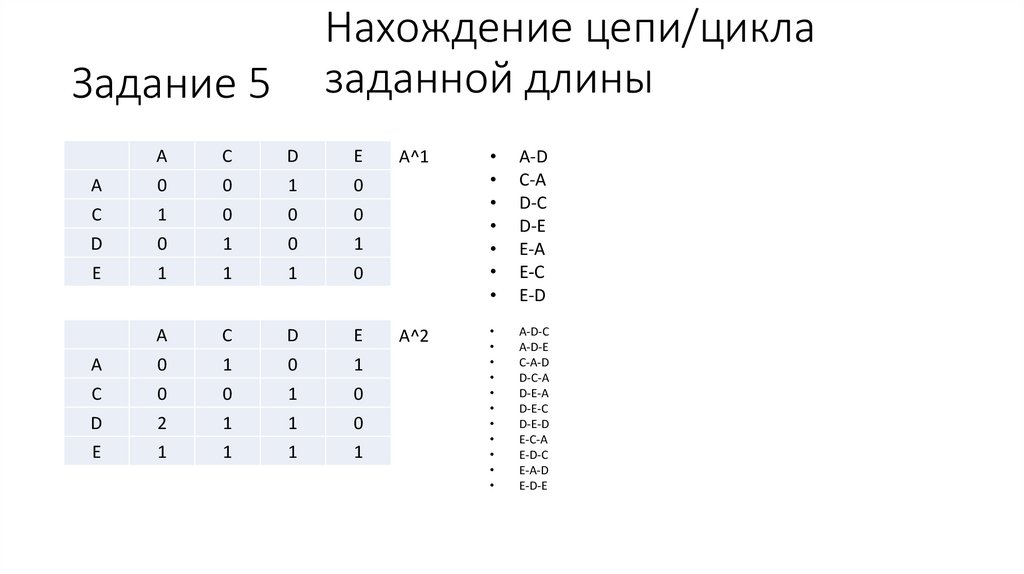
50.

Нахождение цепи/цикла
заданной длины
Задание 5
A
C
D
E
A
0
0
1
0
C
1
0
0
0
D
0
1
0
1
E
1
1
1
0
A
C
D
E
A
0
1
0
1
C
0
0
1
0
D
2
1
1
0
E
1
1
1
1
A^1
A-D
C-A
D-C
D-E
E-A
E-C
E-D
A^2
A-D-C
A-D-E
C-A-D
D-C-A
D-E-A
D-E-C
D-E-D
E-C-A
E-D-C
E-A-D
E-D-E

51.

Нахождение цепи/цикла
заданной длины
Задание 5
A
C
D
E
A
2
1
1
0
C
0
1
0
1
D
1
1
2
1
E
2
2
2
1
A^3
A-D-C-A
A-D-E-A
A-D-E-C
C-A-D-C
C-A-D-E
D-E-C-A
D-E-D-C
D-C-A-D
D-E-A-D
D-E-D-E
E-D-E-A
E-D-C-A
E-A-D-C
E-D-E-C
E-C-A-D
E-D-E-D
E-A-D-E

52.

Нахождение цепи/цикла
заданной длины
Задание 5
A
C
D
E
A
1
1
2
1
C
2
1
1
0
D
2
3
2
2
E
3
3
3
2
A^4
A-D-E-C-A
A-D-E-D-C
A-D-E-A-D
A-D-C-A-D
A-D-E-D-E
C-A-D-C-A
C-A-D-E-A
C-A-D-E-C
C-A-D-E-D
D-E-D-C-A
D-E-D-E-A
D-C-A-D-C
D-E-A-D-C
D-E-D-E-C
D-E-D-E-D
D-E-C-A-D
D-E-A-D-E
D-C-A-D-E
E-D-E-C-A
E-A-D-E-A
E-A-D-C-A
E-A-D-E-C
E-D-E-D-C
E-C-A-D-C
E-A-D-E-D
E-D-C-A-D
E-D-E-A-D
E-C-A-D-E
E-D-E-D-E

53.

Нахождение цепи/цикла
заданной длины
Задание 5
A
C
D
E
A
2
3
2
2
C
1
1
2
1
D
5
4
4
2
E
5
5
5
3
Циклы длины 5 для ССК (A,C,D,E):
A-D-E-D-C-A
A-D-E-D-E-A
C-A-D-E-D-C
D-E-D-C-A-D
D-E-D-E-A-D
D-E-A-D-E-D
D-C-A-D-E-D
E-A-D-E-D-E
E-D-C-A-D-E
E-D-E-A-D-E
A^5
A-D-E-D-C-A
A-D-E-D-E-A
C-A-D-E-D-C
D-E-D-C-A-D
D-E-D-E-A-D
D-E-A-D-E-D
D-C-A-D-E-D
E-A-D-E-D-E
E-D-C-A-D-E
E-D-E-A-D-E

54.

Задание 5
Циклы длины 5 для графа G:
1. G-H-F-H-F-G
2. F-H-F-G-H-F
3. F-G-H-F-H-F
4. H-F-H-F-G-H
5. H-F-G-H-F-H
6. A-D-E-D-C-A
7. A-D-E-D-E-A
8. C-A-D-E-D-C
9. D-E-D-C-A-D
10. D-E-D-E-A-D
11. D-E-A-D-E-D
12. D-C-A-D-E-D
13. E-A-D-E-D-E
14. E-D-C-A-D-E
15. E-D-E-A-D-E
Нахождение цепи/цикла
заданной длины

55.

Алгоритм Дейкстра
Задание 6
A
B
C
D
E
F
G
H
Mark
0
0
0
0
1
0
0
0
D
Inf
Inf
Inf
Inf
0
Inf
Inf
inf
P
5
5
5
5
5
5
5
5
Источник алгоритма Дейкстры: E
Искомое значение: P[4]
P[4] – вершина, в которую необходимо пойти, чтобы попасть в вершину E из вершины E.
Для источника это значение равно самому себе, поэтому нет смысла прогонять алгоритм целиком.
Можно сразу сказать, что P[4] = 5 (вершина E).

56.

Задание 6. Методы построения ОДМС:
алгоритм Прима
Изображение
3
a
2
7
b
6
Ребро (u, v)
Множество
невыбранных
вершин V \ U
Описание
{a, b, c, d, e}
Исходный взвешенный
граф. Числа возле ребер
показывают их веса,
которые можно
рассматривать как
расстояния между
e
6
10
Множество
выбранных
вершин U
c 1
12
{}
d
2
вершинами.
3
a
10
2
7
b
6
e
6
c 1
2
12
d
{a}
(a, b)=2 +
(a, c)=10
(a, d)=7
(a, e)=3
{b, c, d, e}
В качестве начальной
выбирается вершина a.
Каждая из вершин b, c, d и e
соединена с a единственным
ребром. Вершина b —
ближайшая к a, и
выбирается как вторая
вершина вместе с ребром
ab.

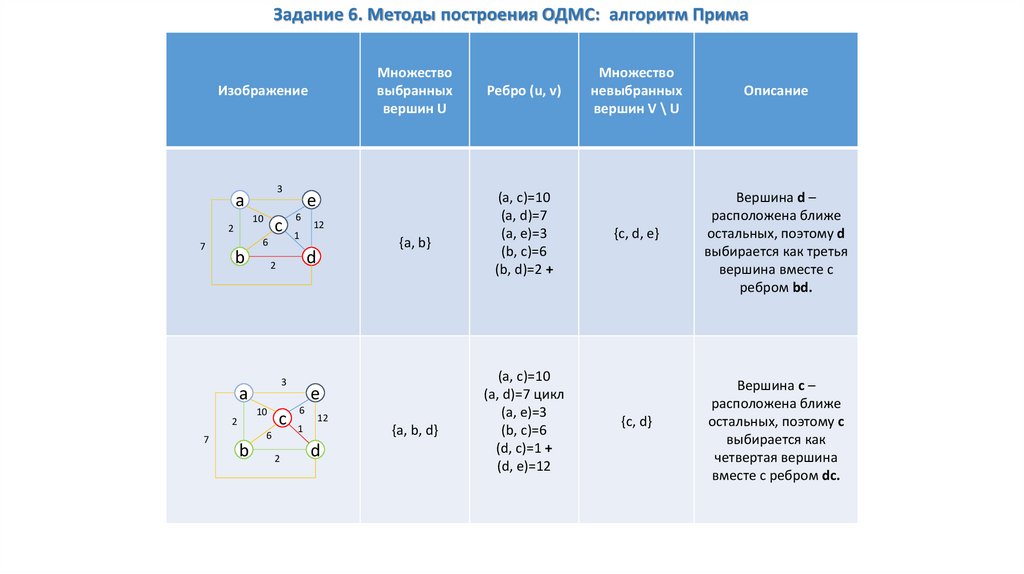
57.

Задание 6. Методы построения ОДМС: алгоритм Прима
Множество
выбранных
вершин U
Изображение
3
a
7
6
10
2
b
c 1
6
3
10
7
b
6
12
{a, b}
d
2
a
2
e
e
6
c 1
2
12
d
{a, b, d}
Ребро (u, v)
(a, c)=10
(a, d)=7
(a, e)=3
(b, c)=6
(b, d)=2 +
(a, c)=10
(a, d)=7 цикл
(a, e)=3
(b, c)=6
(d, c)=1 +
(d, e)=12
Множество
невыбранных
вершин V \ U
{c, d, e}
{c, d}
Описание
Вершина d –
расположена ближе
остальных, поэтому d
выбирается как третья
вершина вместе с
ребром bd.
Вершина c –
расположена ближе
остальных, поэтому c
выбирается как
четвертая вершина
вместе с ребром dc.

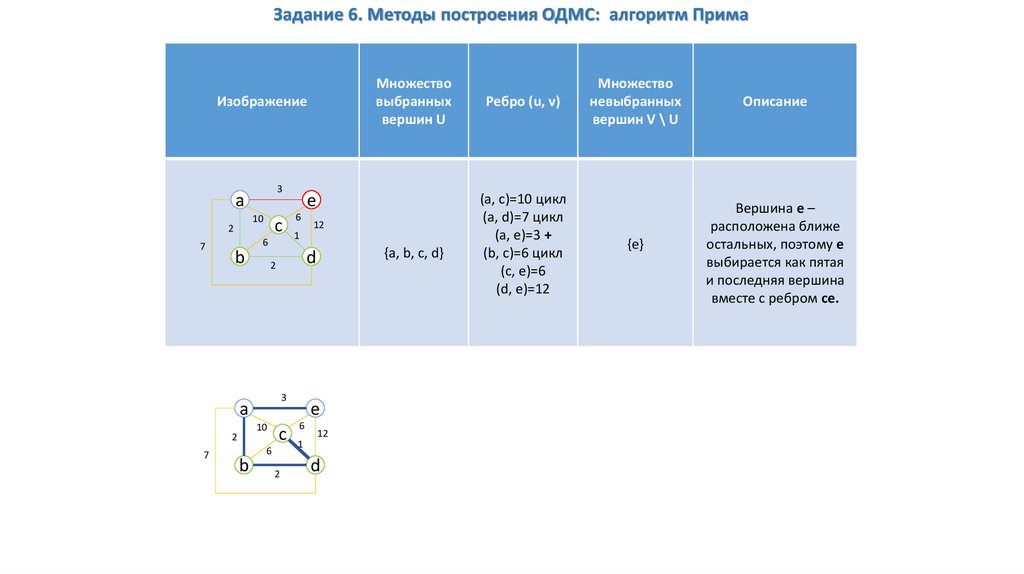
58.

Задание 6. Методы построения ОДМС: алгоритм Прима
Множество
выбранных
вершин U
Изображение
3
a
10
2
7
b
c 1
6
2
3
10
7
b
6
12
{a, b, c, d}
d
a
2
e
6
e
6
c 1
2
12
d
Ребро (u, v)
(a, c)=10 цикл
(a, d)=7 цикл
(a, e)=3 +
(b, c)=6 цикл
(c, e)=6
(d, e)=12
Множество
невыбранных
вершин V \ U
{e}
Описание
Вершина e –
расположена ближе
остальных, поэтому e
выбирается как пятая
и последняя вершина
вместе с ребром ce.

59.

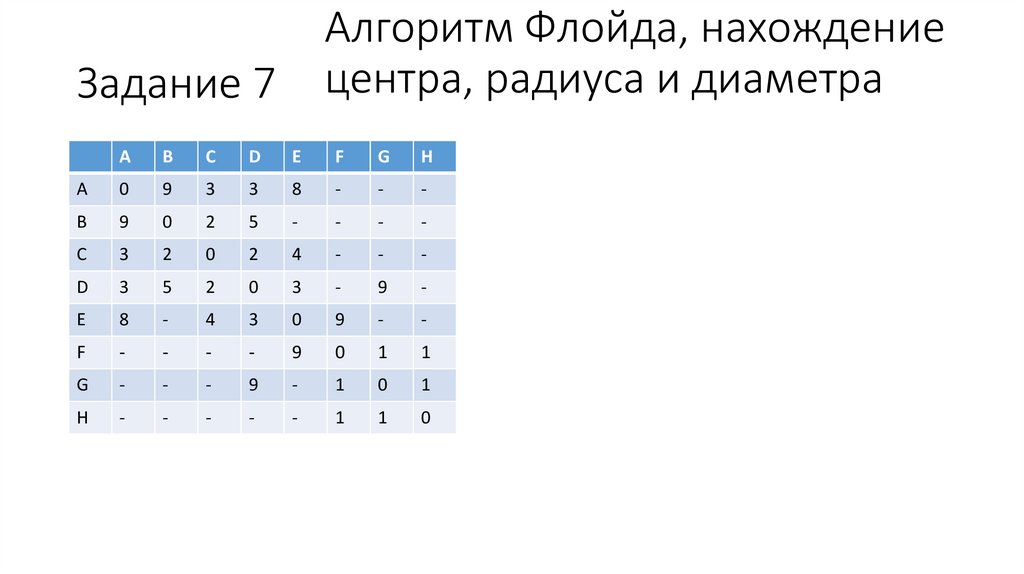
Алгоритм Флойда, нахождение
центра, радиуса и диаметра
Задание 7
A
B
C
D
E
F
G
H
A
0
9
3
3
8
-
-
-
B
9
0
2
5
-
-
-
-
C
3
2
0
2
4
-
-
-
D
3
5
2
0
3
-
9
-
E
8
-
4
3
0
9
-
-
F
-
-
-
-
9
0
1
1
G
-
-
-
9
-
1
0
1
H
-
-
-
-
-
1
1
0

60.

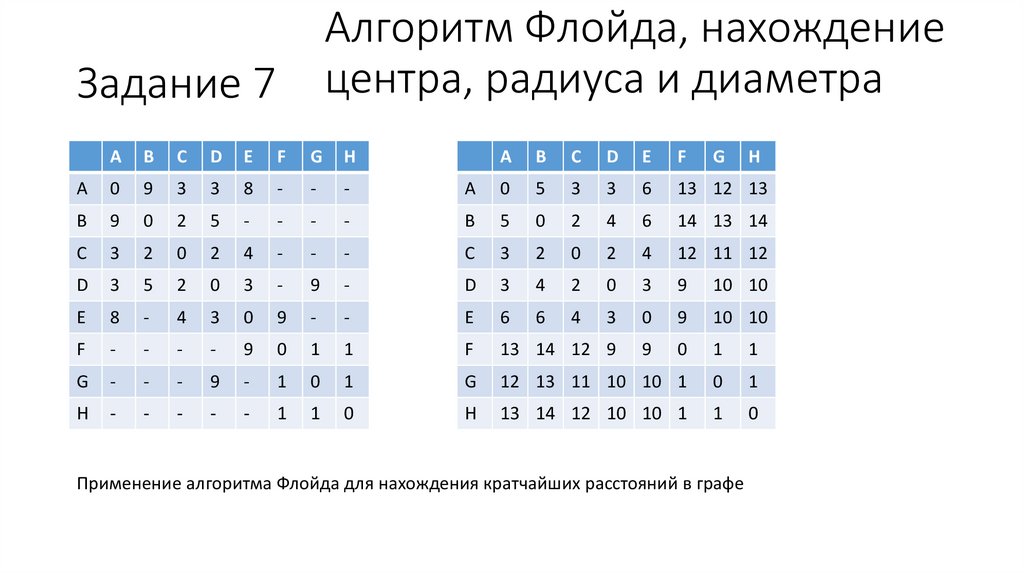
Алгоритм Флойда, нахождение
центра, радиуса и диаметра
Задание 7
A
B
C
D
E
F
G
H
A
B
C
D
E
F
A
0
9
3
3
8
-
-
-
B
9
0
2
5
-
-
-
C
3
2
0
2
4
-
D
3
5
2
0
3
E
8
-
4
3
F
-
-
-
G
-
-
H
-
-
G
A
0
5
3
3
6
13 12 13
-
B
5
0
2
4
6
14 13 14
-
-
C
3
2
0
2
4
12 11 12
-
9
-
D
3
4
2
0
3
9
10 10
0
9
-
-
E
6
6
4
3
0
9
10 10
-
9
0
1
1
F
13 14 12 9
9
0
1
1
-
9
-
1
0
1
G
12 13 11 10 10 1
0
1
-
-
-
1
1
0
H
13 14 12 10 10 1
1
0
Применение алгоритма Флойда для нахождения кратчайших расстояний в графе
H

61.

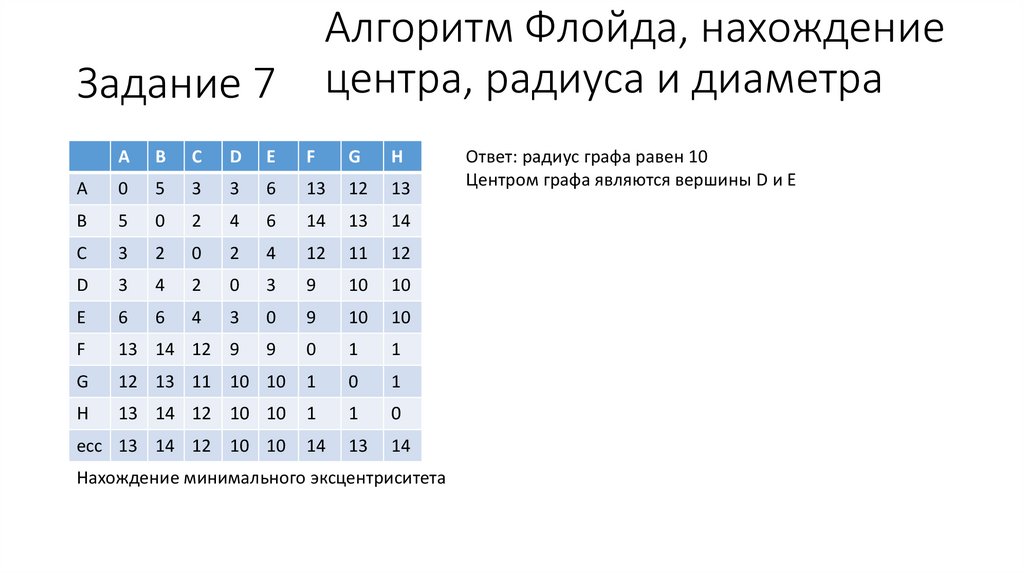
Алгоритм Флойда, нахождение
центра, радиуса и диаметра
Задание 7
A
B
C
D
E
F
G
H
A
0
5
3
3
6
13
12
13
B
5
0
2
4
6
14
13
14
C
3
2
0
2
4
12
11
12
D
3
4
2
0
3
9
10
10
E
6
6
4
3
0
9
10
10
F
13 14 12 9
9
0
1
1
G
12 13 11 10 10
1
0
1
H
13 14 12 10 10
1
1
0
ecc 13 14 12 10 10
14
13
14
Нахождение минимального эксцентриситета
Ответ: радиус графа равен 10
Центром графа являются вершины D и E

62.

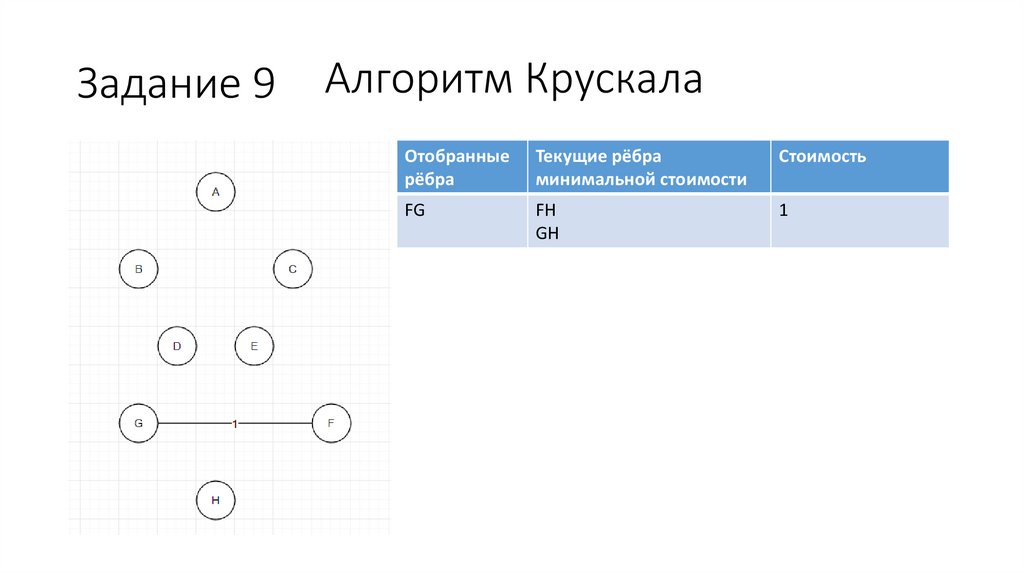
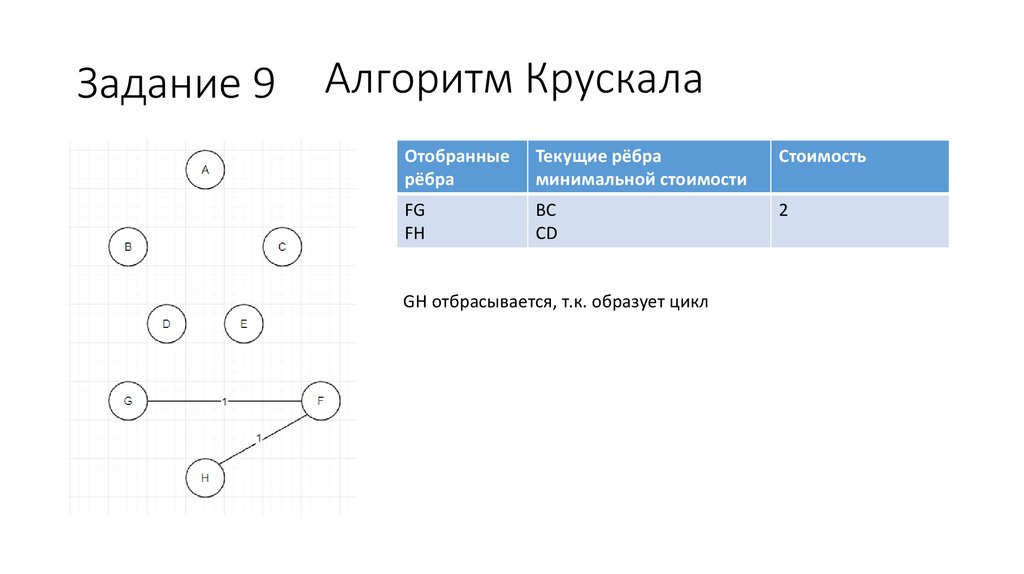
Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
GH
1

63.

Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
GH
1

64.

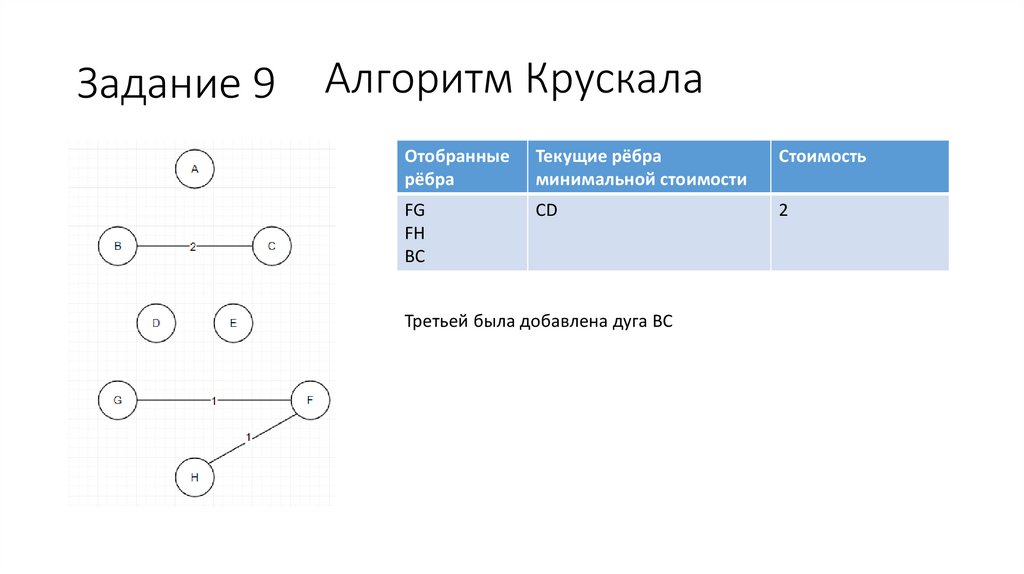
Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
2
GH отбрасывается, т.к. образует цикл

65.

Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
2
Третьей была добавлена дуга BC

66.

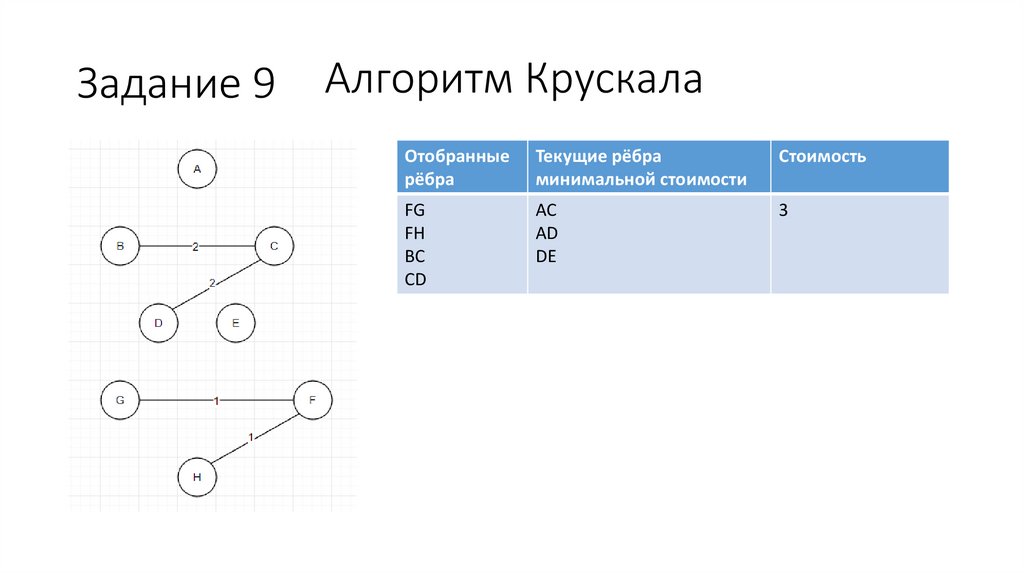
Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
AC
AD
DE
3

67.

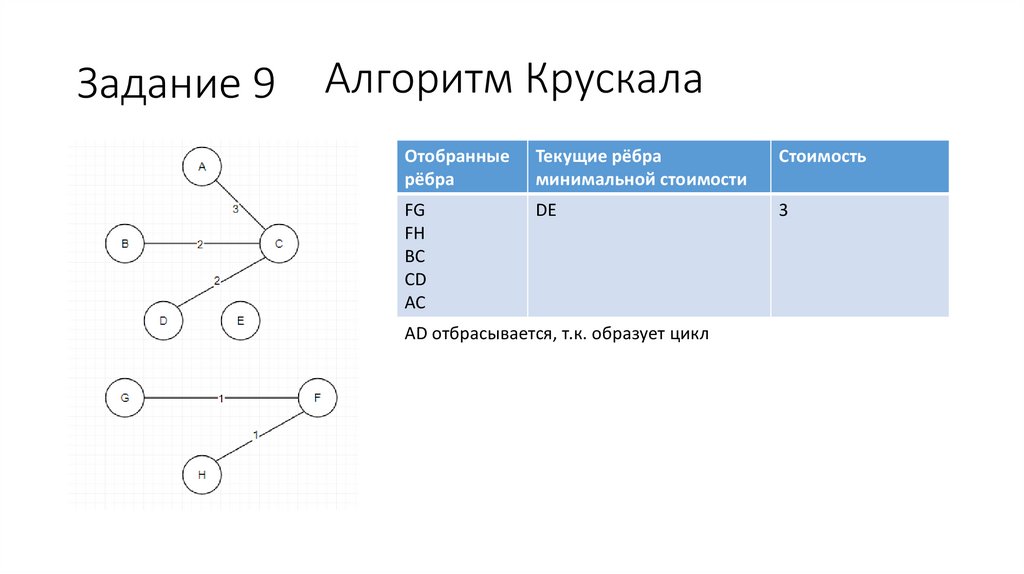
Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
AC
DE
3
AD отбрасывается, т.к. образует цикл

68.

Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
AC
DE
DG
EF
9
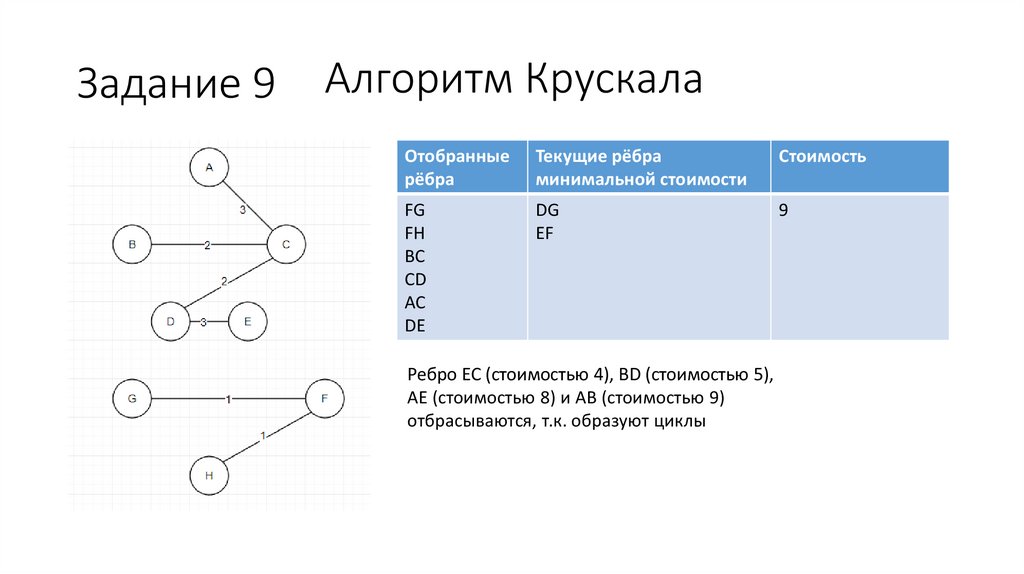
Ребро EC (стоимостью 4), BD (стоимостью 5),
AE (стоимостью 8) и AB (стоимостью 9)
отбрасываются, т.к. образуют циклы

69.

Задание 9
Алгоритм Крускала
Отобранные
рёбра
Текущие рёбра
минимальной стоимости
Стоимость
FG
FH
BC
CD
AC
DE
DG
EF
9
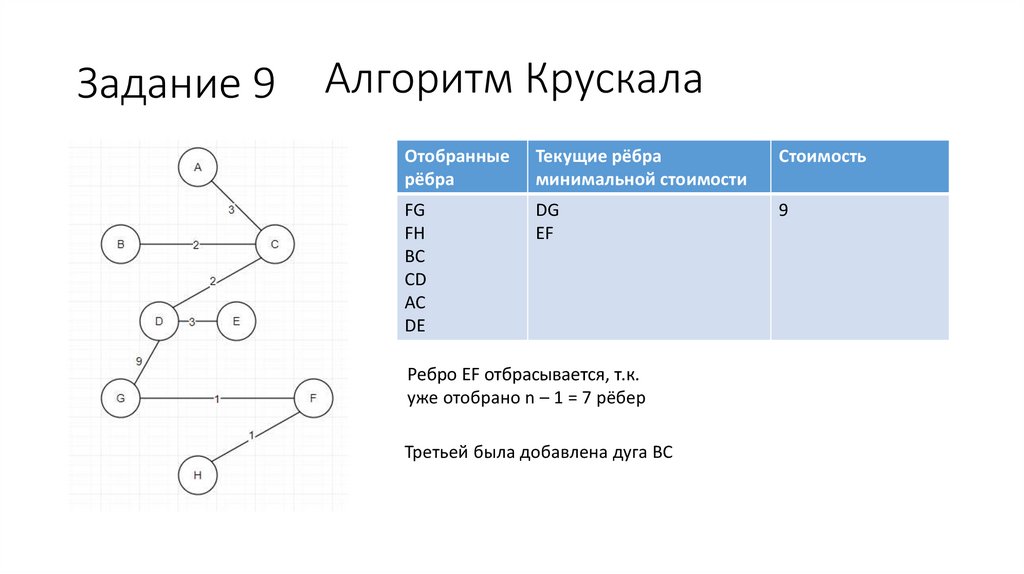
Ребро EF отбрасывается, т.к.
уже отобрано n – 1 = 7 рёбер
Третьей была добавлена дуга BC

70.

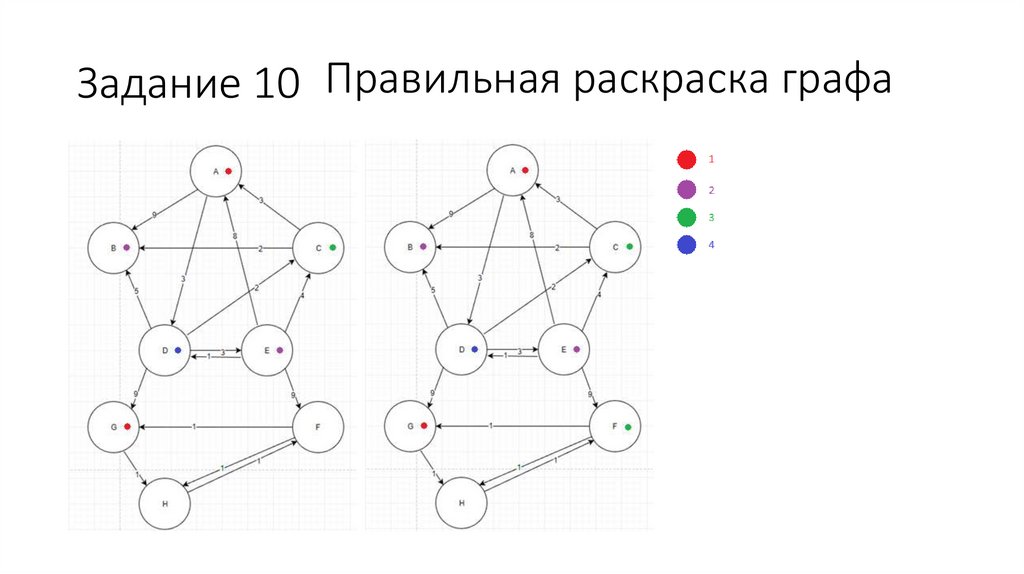
Задание 10 Правильная раскраска графа

71.

Задание 10 Правильная раскраска графа

72.

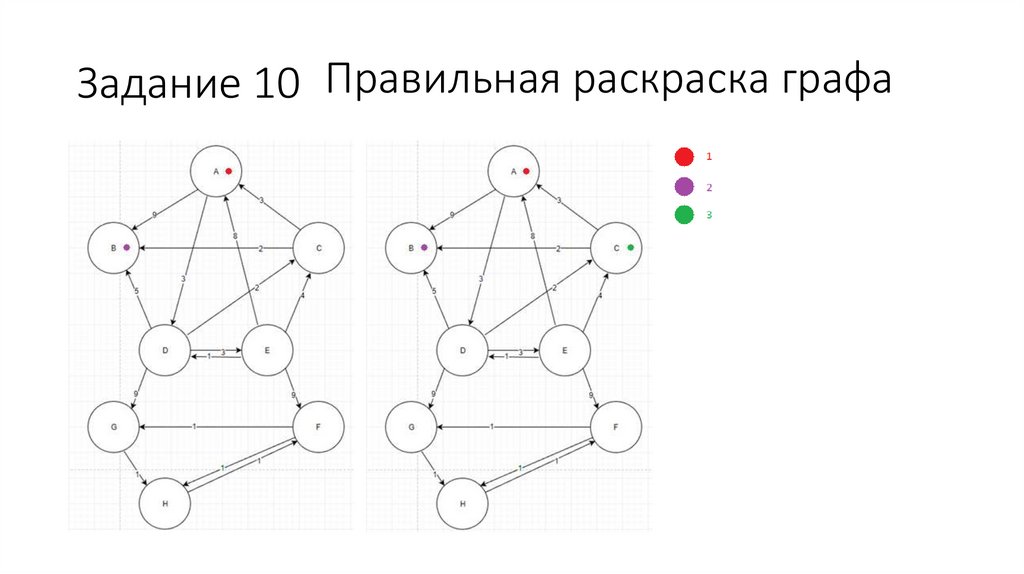
Задание 10 Правильная раскраска графа

73.

Задание 10 Правильная раскраска графа

74.

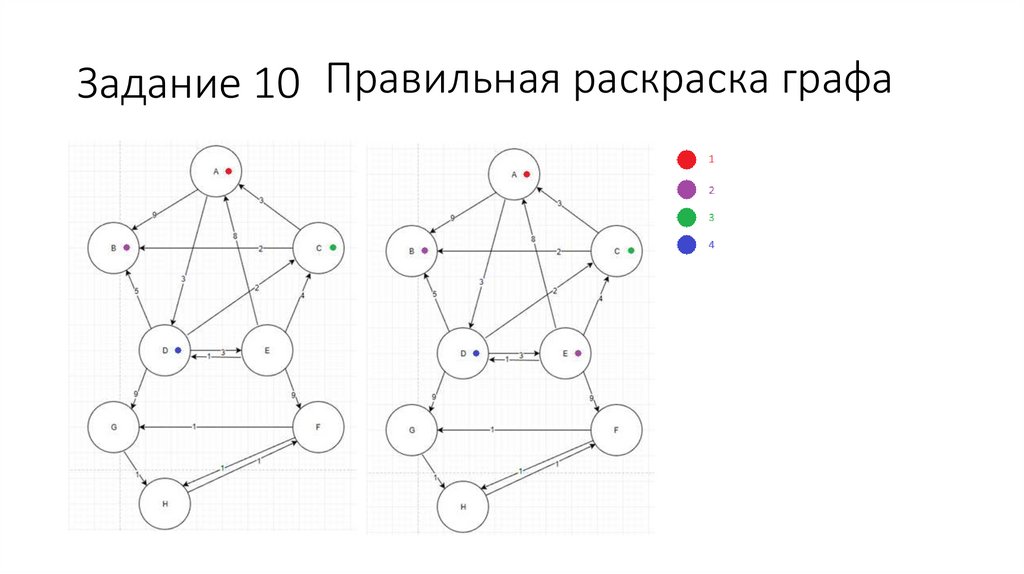
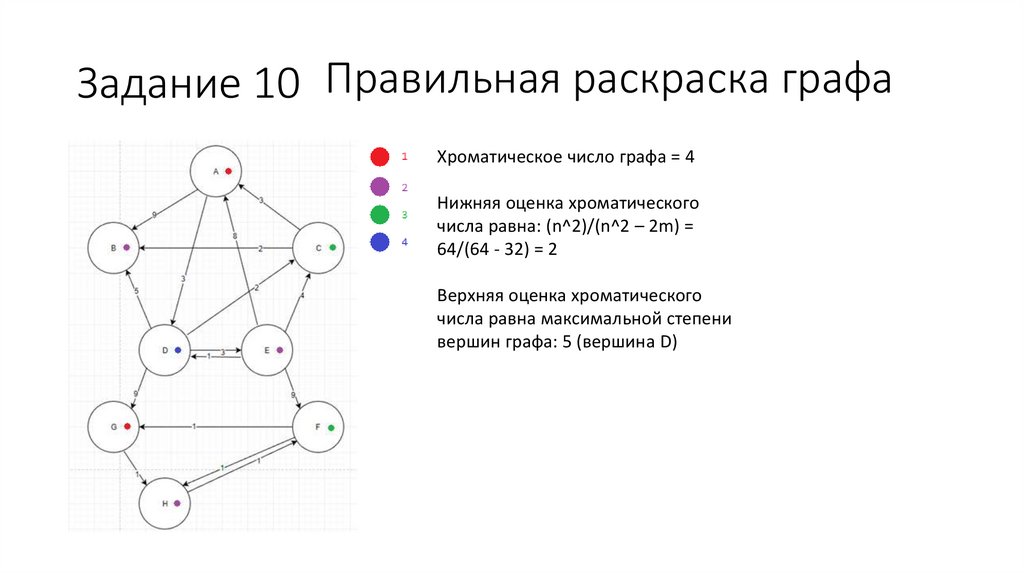
Задание 10 Правильная раскраска графа
Хроматическое число графа = 4
Нижняя оценка хроматического
числа равна: (n^2)/(n^2 – 2m) =
64/(64 - 32) = 2
Верхняя оценка хроматического
числа равна максимальной степени
вершин графа: 5 (вершина D)

75.

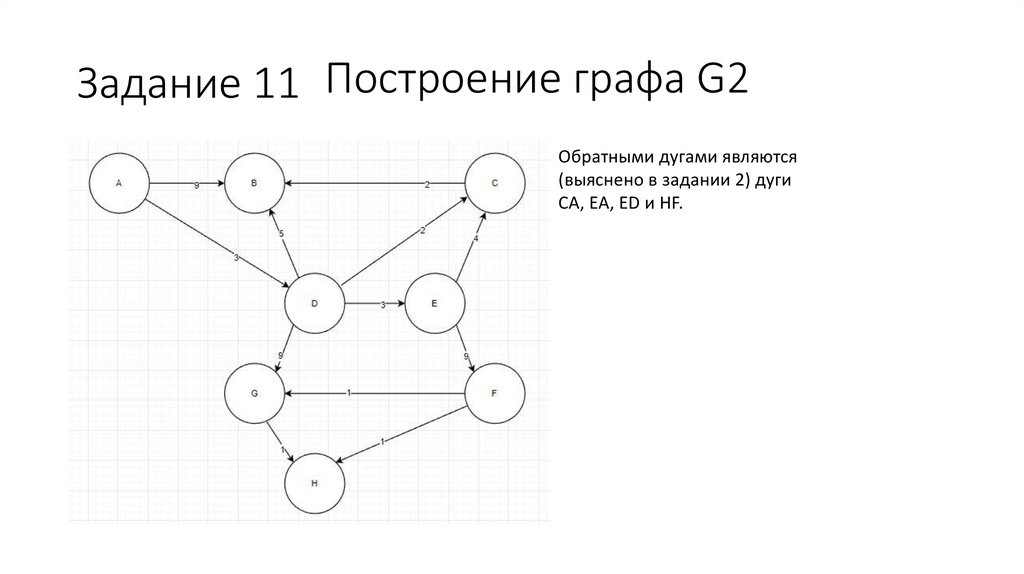
Задание 11 Построение графа G2
Обратными дугами являются
(выяснено в задании 2) дуги
CA, EA, ED и HF.

76.

Задание 11 Построение графа G2
0
1
0
1
0
0
0
0
0
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
0
0
1
0
0
0
1
1
0
0
1
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Матрица смежности
Матрица транзитивного замыкания
Вычислена алгоритмом Уоршала

77.

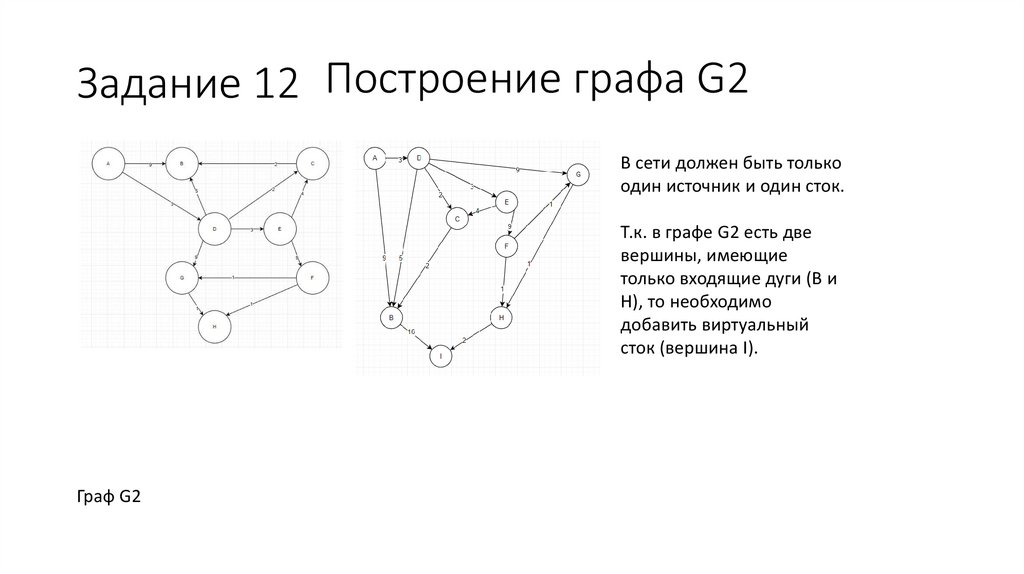
Задание 12 Построение графа G2
В сети должен быть только
один источник и один сток.
Т.к. в графе G2 есть две
вершины, имеющие
только входящие дуги (B и
H), то необходимо
добавить виртуальный
сток (вершина I).
Граф G2

78.

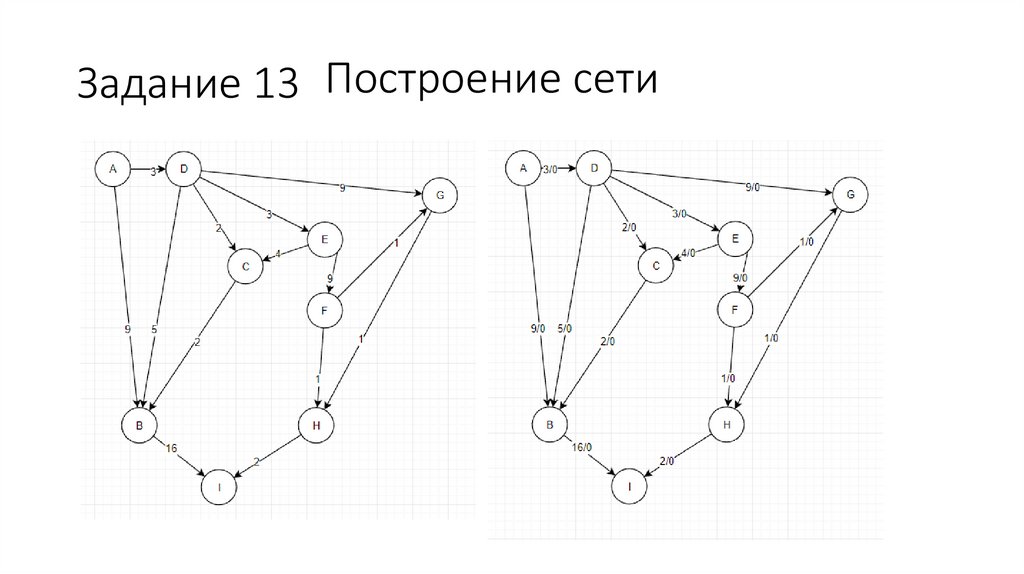
Задание 13 Построение сети

79.

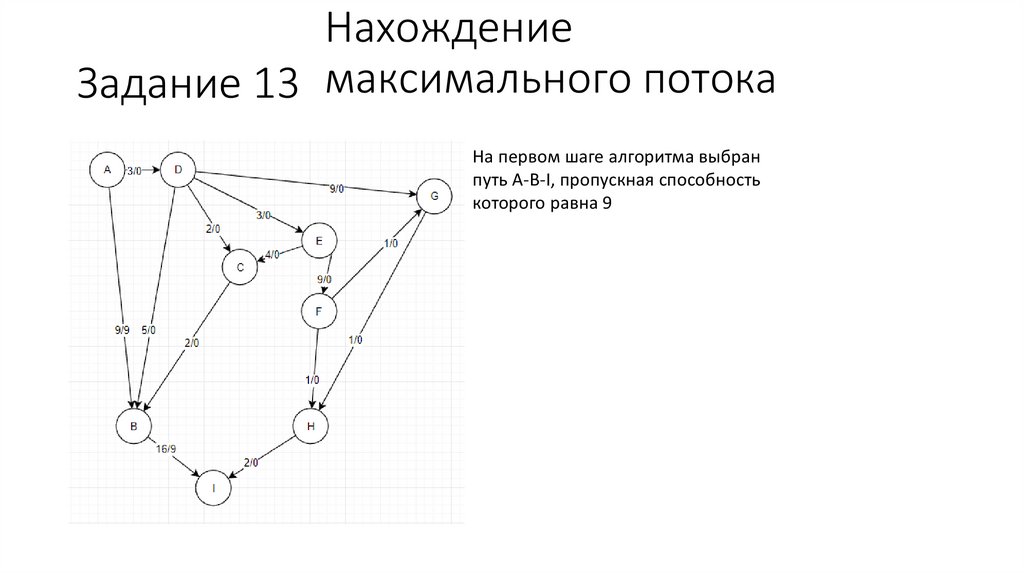
Нахождение
Задание 13 максимального потока
На первом шаге алгоритма выбран
путь A-B-I, пропускная способность
которого равна 9

80.

Нахождение
Задание 13 максимального потока
На следующем шаге стоится сеть G’.
При этом дуга AB инвертируется, т.к.
была полностью заполнена на
предыдущем шаге, а дуга BI
расщепляется на две дуги, давая
алгоритму путь для отмены
предыдущих решений.

81.

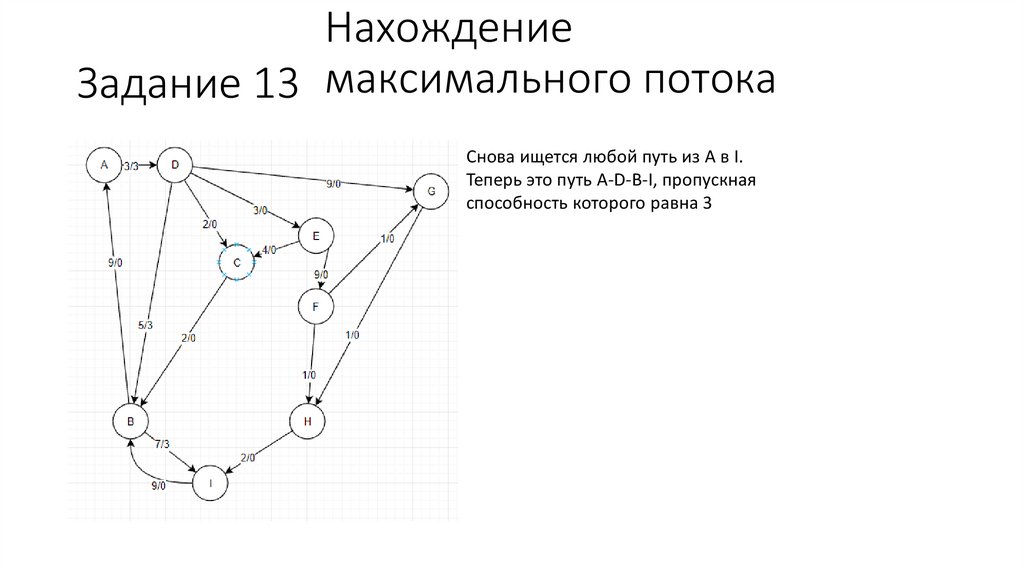
Нахождение
Задание 13 максимального потока
Снова ищется любой путь из A в I.
Теперь это путь A-D-B-I, пропускная
способность которого равна 3

82.

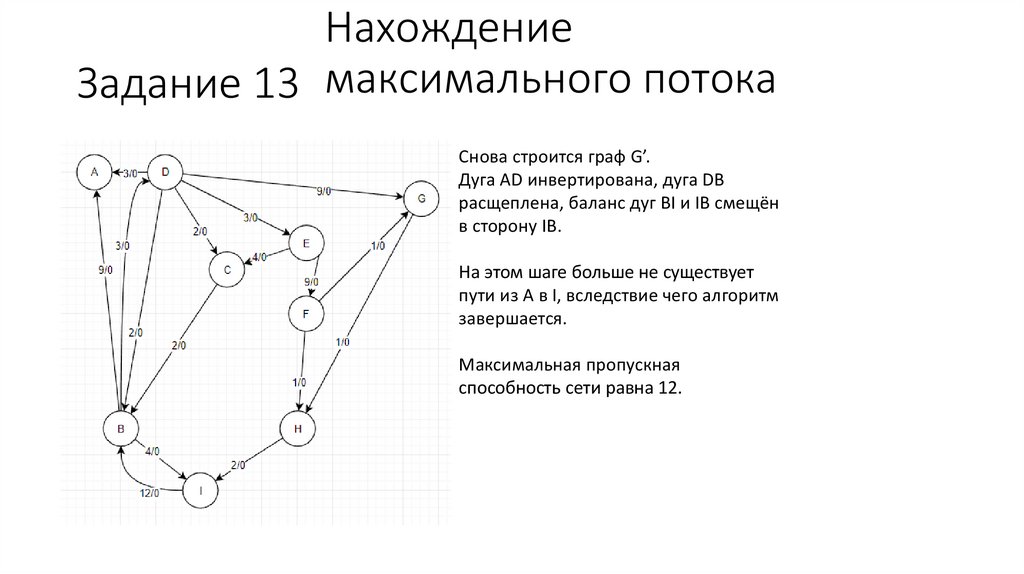
Нахождение
Задание 13 максимального потока
Снова строится граф G’.
Дуга AD инвертирована, дуга DB
расщеплена, баланс дуг BI и IB смещён
в сторону IB.
На этом шаге больше не существует
пути из A в I, вследствие чего алгоритм
завершается.
Максимальная пропускная
способность сети равна 12.

83.

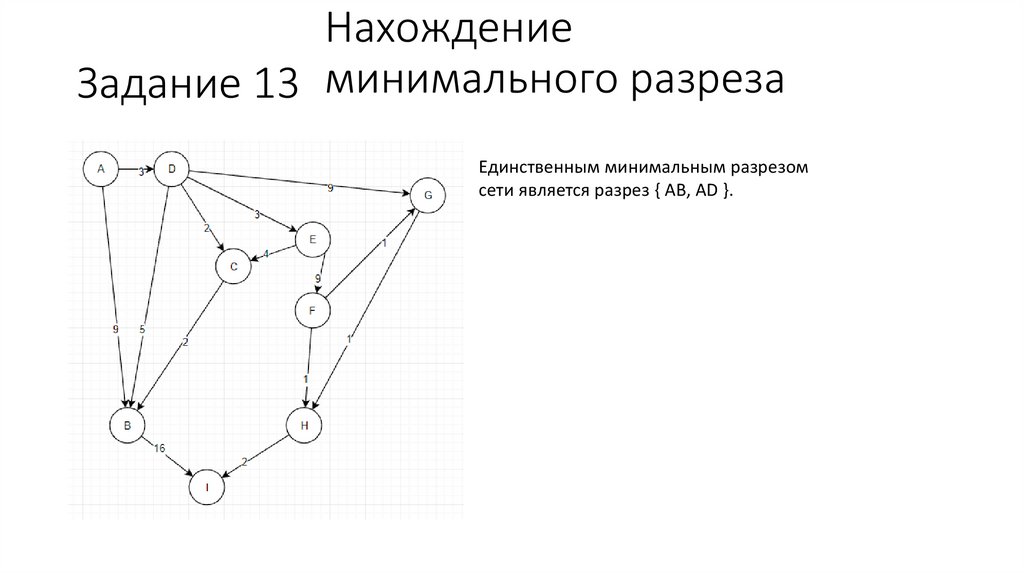
Нахождение
Задание 13 минимального разреза
Единственным минимальным разрезом
сети является разрез { AB, AD }.

84.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
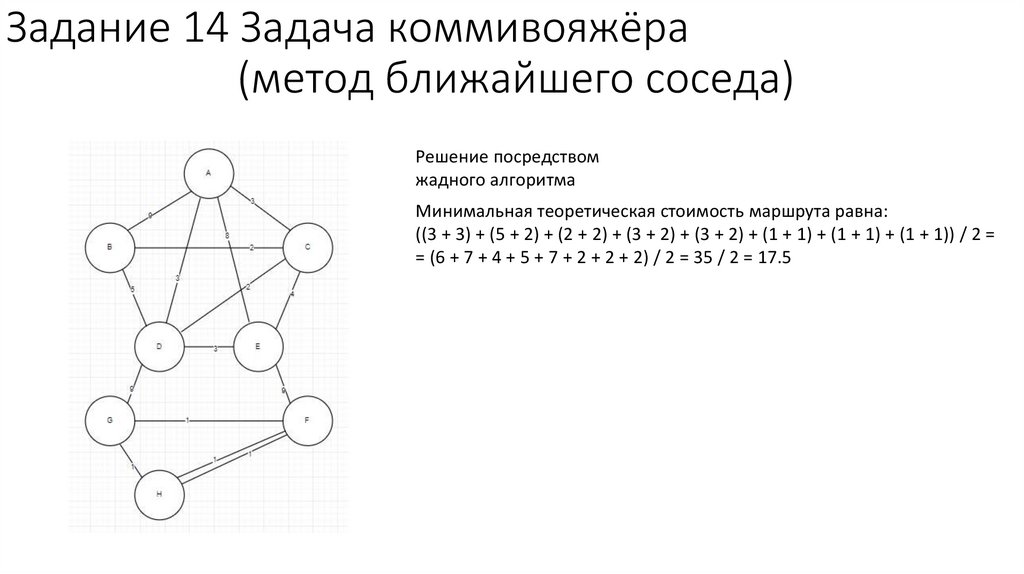
Решение посредством
жадного алгоритма
Минимальная теоретическая стоимость маршрута равна:
((3 + 3) + (5 + 2) + (2 + 2) + (3 + 2) + (3 + 2) + (1 + 1) + (1 + 1) + (1 + 1)) / 2 =
= (6 + 7 + 4 + 5 + 7 + 2 + 2 + 2) / 2 = 35 / 2 = 17.5

85.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V Доступные дуги
A
B, C, D, E, F, G, H A
AB (9)
AC (3)
AD (3)
AE (8)

86.

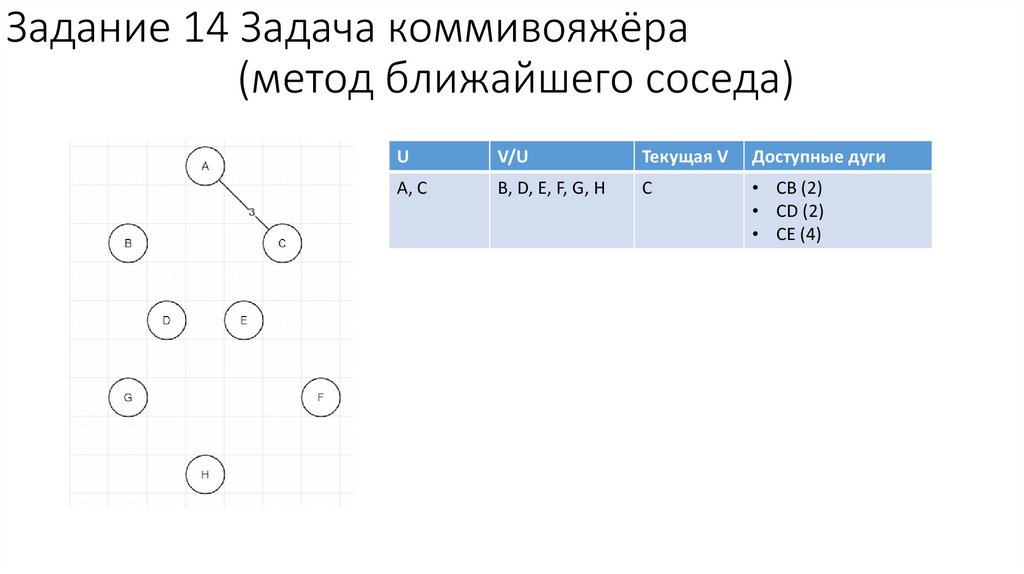
Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C
B, D, E, F, G, H
C
• CB (2)
• CD (2)
• CE (4)

87.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C, B
D, E, F, G, H
B
• BD (5)

88.

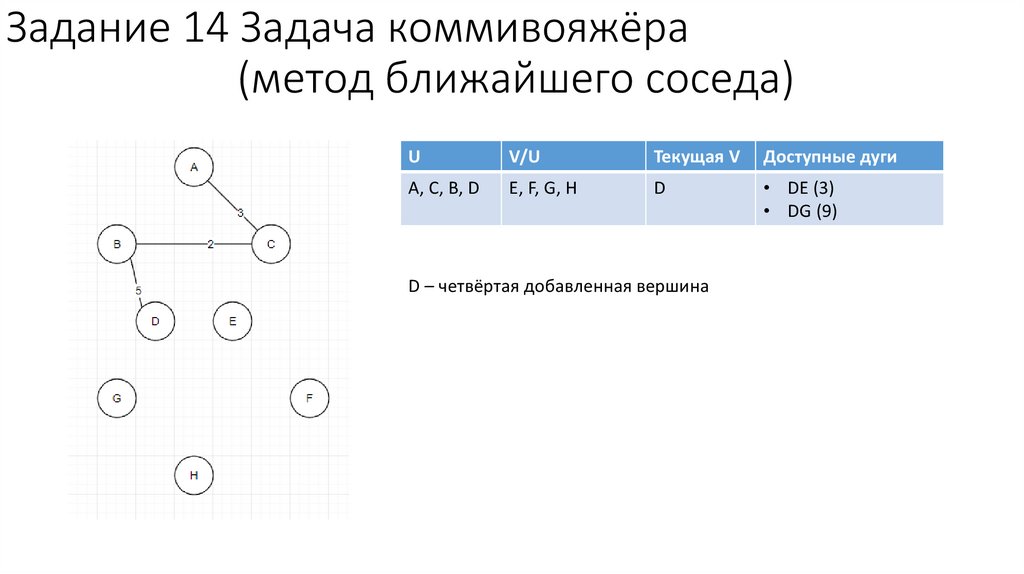
Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C, B, D
E, F, G, H
D
• DE (3)
• DG (9)
D – четвёртая добавленная вершина

89.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C, B, D, E
F, G, H
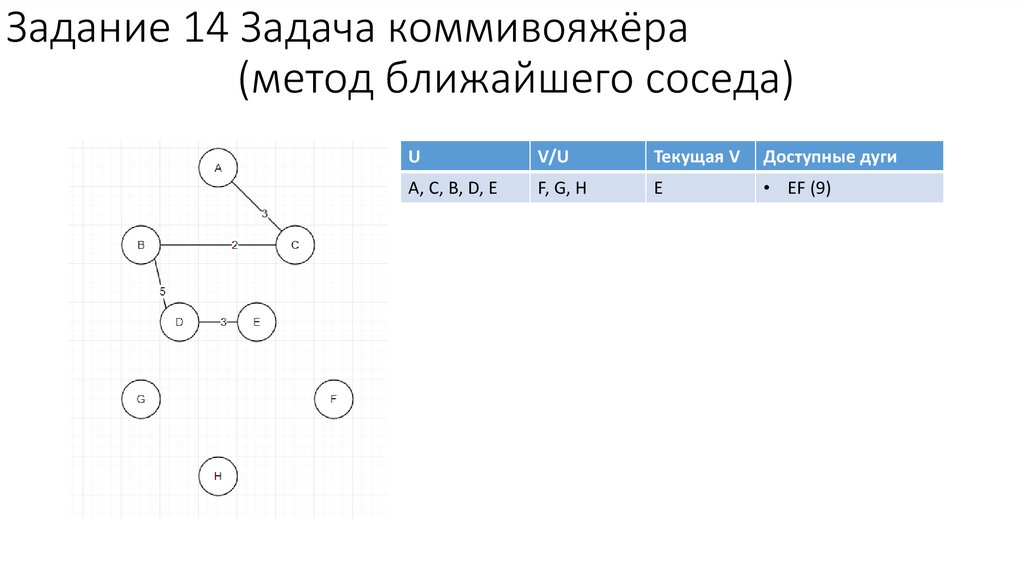
E
• EF (9)

90.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C, B, D, E, F
G, H
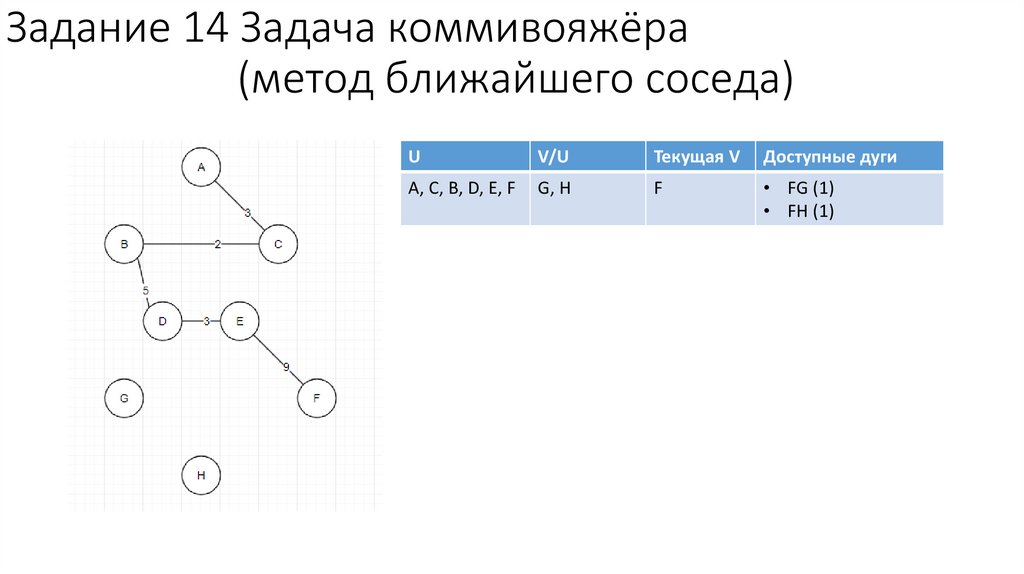
F
• FG (1)
• FH (1)

91.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
V/U
Текущая V
Доступные дуги
A, C, B, D, E, F, G
H
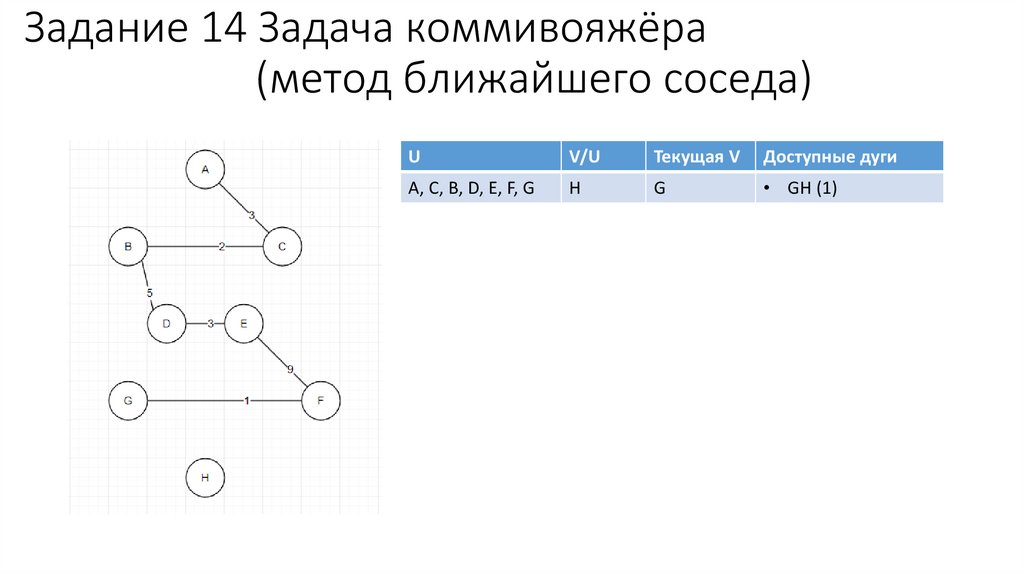
G
• GH (1)

92.

Задание 14 Задача коммивояжёра
(метод ближайшего соседа)
U
A, C, B, D, E, F, G, H
V/U
Текущая V
Доступные дуги
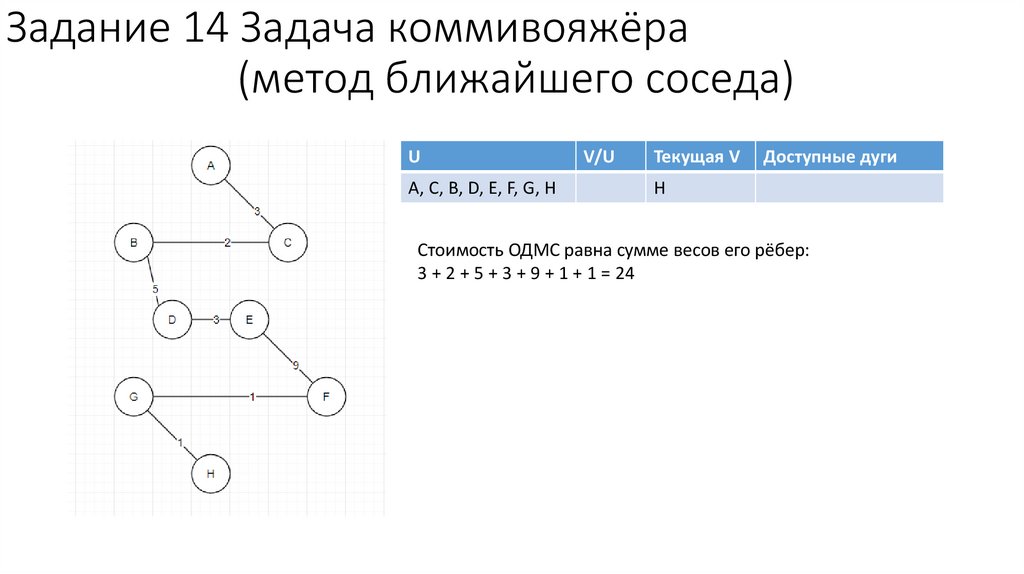
H
Стоимость ОДМС равна сумме весов его рёбер:
3 + 2 + 5 + 3 + 9 + 1 + 1 = 24

93.

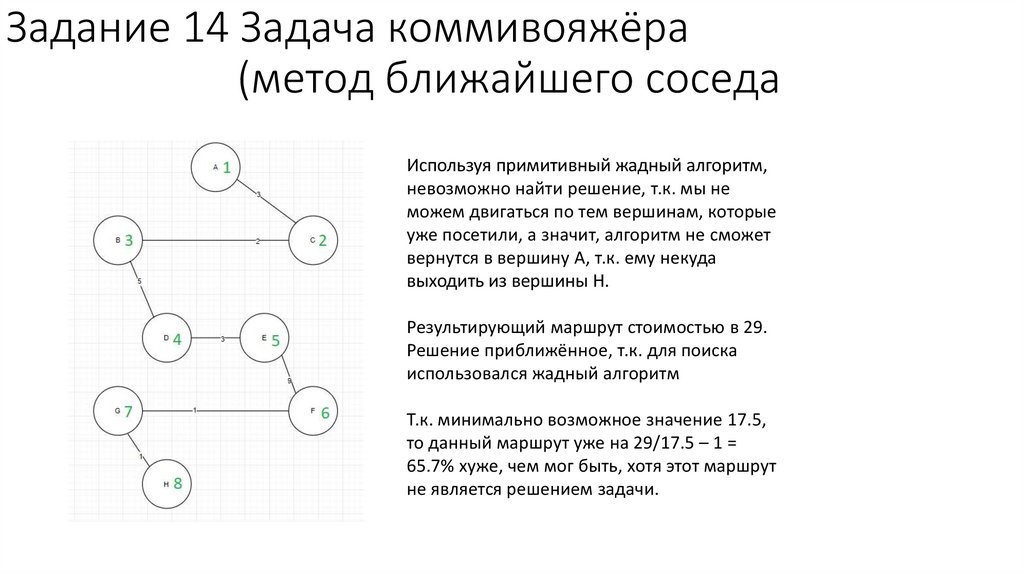
Задание 14 Задача коммивояжёра
(метод ближайшего соседа
Используя примитивный жадный алгоритм,
невозможно найти решение, т.к. мы не
можем двигаться по тем вершинам, которые
уже посетили, а значит, алгоритм не сможет
вернутся в вершину A, т.к. ему некуда
выходить из вершины H.
Результирующий маршрут стоимостью в 29.
Решение приближённое, т.к. для поиска
использовался жадный алгоритм
Т.к. минимально возможное значение 17.5,
то данный маршрут уже на 29/17.5 – 1 =
65.7% хуже, чем мог быть, хотя этот маршрут
не является решением задачи.