Множество и подмножество. Операции над множествами

1. Множество и подмножество. Операции над множествами

2.

При изучении параграфа «Множества и
операции над ними» вы познакомитесь с
начальными понятиями общепринятого
в математике языка теории множеств:
-элемент множества;
-подмножество данного множества;
-объединение множеств;
-пересечение множеств.

3.

Объекты, составляющие множество, называются
элементами множества.
Среди множеств выделяют особое множество пустое множество.
Пустое множество- множество, не содержащее ни
одного элемента.
Пустое множество является частью любого множества.
Примеры пустых множеств.
Решение:
1) Множество квадратных уравнений, которые имеют более
двух разных корней;
2) множество простых делителей числа 1;
3) множество точек пересечения двух параллельных прямых;
4) множество прямых углов равностороннего треугольника;
5) множество людей на Солнце;
6) множество двузначных положительных чисел,
расположенных на числовом луче левее 9.

4.

Множество состоит из элементов. Если этих элементов
немного, то удобно все элементы просто перечислить в
каком-нибудь порядке. Чтобы не забыть, что перечисляемые
элементы объединены в некоторое множество, такое
перечисление производят внутри фигурных скобок { , }.
Словесное описание
множества
Поэлементное
описание множества
Задание множества
перечислением его
элементов
Цифры десятичной
системы счисления
Множество состоит из
цифр 0, 1, 2, 3, 4, 5, 6,
7, 8, 9
{0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
Гласные буквы
русского алфавита
Множество букв
состоит из букв А, Е,
Ё, И, О, У, Ы, Э, Ю, Я
{А, Е, Ё, И, О, У, Ы, Э,
Ю, Я}
Корни уравнения
Х2 + 10х = 39
Множество состоит из
чисел 3 и -13
{3 ; -13}
Президенты
Российской
Федерации
Множество состоит из
трех людей: Ельцин,
Путин, Медведев
{Ельцин, Путин,
Медведев}

5.

Множества, элементами которых являются числа,
называются числовыми множествами.
Пример
Множество А состоит из всех корней уравнения х3 + х2 – 6х = 0
1) Решить это уравнение.
2) Задать множество А перечислением его элементов.
3) Записать все возможные способы перечисления элементов множества А.
4) Сколько всего имеется способов перечисления элементов множества А?
Решение:
1) х3 + х2 – 6х = 0
2)А={-3; 0; 2}
х(х2 + х – 6) = 0
х(х + 3)(х – 2) = 0
х=0; х=-3; х=2
3) {-3; 0; 2} , {-3; 2; 0},
{0; 2; -3}, {0; -3; 2},
{2; -3; 0}, {2; 0; -3}
4) 6

6.

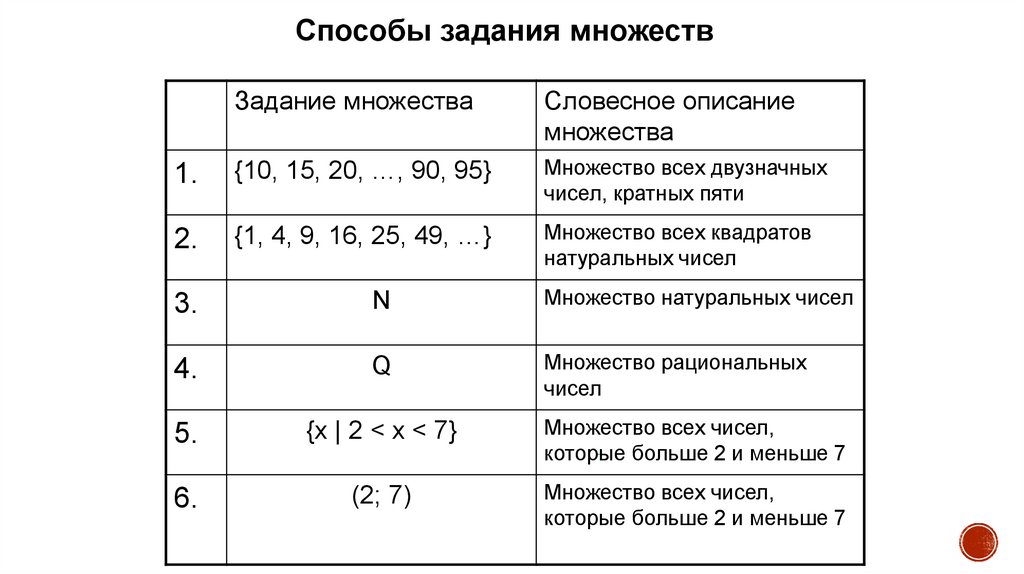
Способы задания множеств
Задание множества
Словесное описание
множества
1.
{10, 15, 20, …, 90, 95}
Множество всех двузначных
чисел, кратных пяти
2.
{1, 4, 9, 16, 25, 49, …}
Множество всех квадратов
натуральных чисел
3.
N
Множество натуральных чисел
4.
Q
Множество рациональных
чисел
5.
{х | 2 < x < 7}
Множество всех чисел,
которые больше 2 и меньше 7
6.
(2; 7)
Множество всех чисел,
которые больше 2 и меньше 7

7.

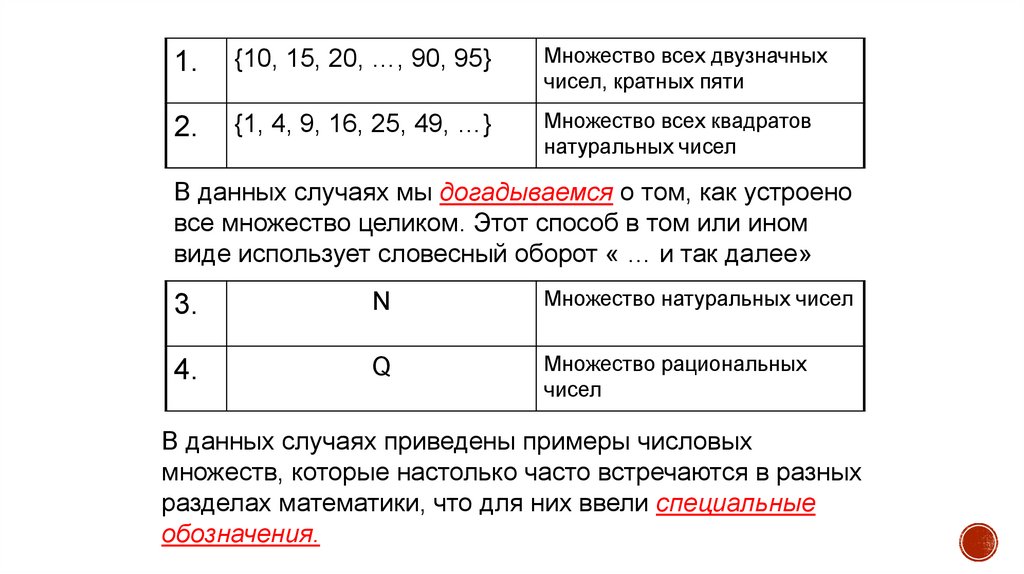
1.
{10, 15, 20, …, 90, 95}
Множество всех двузначных
чисел, кратных пяти
2.
{1, 4, 9, 16, 25, 49, …}
Множество всех квадратов
натуральных чисел
В данных случаях мы догадываемся о том, как устроено
все множество целиком. Этот способ в том или ином
виде использует словесный оборот « … и так далее»
3.
N
Множество натуральных чисел
4.
Q
Множество рациональных
чисел
В данных случаях приведены примеры числовых
множеств, которые настолько часто встречаются в разных
разделах математики, что для них ввели специальные
обозначения.

8.

5.
{х | 2 < x < 7}
Множество всех чисел,
которые больше 2 и меньше 7
6.
(2; 7)
Множество всех чисел,
которые больше 2 и меньше 7
В случае 5 множество задано с помощью его
характеристического свойства (самый распространенный
способ)
Чтение записи
Символы
Как они читаются
{…}
Множество …
{х …}
Множество всех х…
{х | …}
Множество всех х таких, что …
{х | 2 < x < 7}
Множество всех х таких, что 2 < x < 7

9.

Пример
По указанному заданию множества дать его словесное
описание:
а) {0, 2, 4, 6, 8}
Множество всех четных цифр (все цифры, кроме 1,3,5,7,9)
б) {2, 4, 6, … 18, 20}
Множество всех четных натуральных чисел, которые меньше 21
( все числа, полученные из чисел 1, 2, … 9, 10 умножением на 2)
в) {12, 22, 32, … 92}
Множество всех двузначных чисел, оканчивающихся на 2
г) {1, 8, 27, 64, 125, …}
Множество всех кубов натуральных чисел

10.

Пример
Решив соответствующее неравенство, составить более
привычную запись числового множества:
а) {х | х2 + 1 >0}; б) {х | х2 + 1 < 0,5}; в) {х | 1/х >0};
г) {х | 35х2 < 24x +35}
Ответы:
а) (-∞; +∞) или R
б) Ø (пустое множество)
в) (0; 1)
г) [-5/7; 7/5]

11.

Элементы, образующие множество А, можно
объединять не сразу все вместе, а группируя их в
разных комбинациях. Так можно получать различные
подмножества данного множества.
Пример
На поле в составе футбольной команды должны выйти
два нападающих, а у тренера команды есть четыре
кандидата х, у, z, t на эти позиции.
а) Из скольких вариантов придется выбирать тренеру?
б) Как изменится ответ в а), если игрок х не может играть
с игроком у?
в) Как изменится ответ в а), если игрок z может играть
только вместе с игроком t?
г) Как изменится ответ в а), если на поле должны выйти
три нападающих?

12.

Решение:
А = {х, у, z, t} – это множество, из которого тренеру следует выбрать
двух игроков, т.е. выбрать два элемента. Значит, задача свелась к
подсчету числа всех двухэлементных подмножеств данного множества
А = {х, у, z, t}
а) Для игрока х: {х, у}, {х, z}, {х, t}
Для игрока у: {у, z}, {у, t}, вариант {х, у} – уже учтен.
Для игрока z: {z, t}, варианты {х, z}, {у, z} –уже учтены.
Для игрока t все варианты выхода на игру уже указаны
Ответ: 6 вариантов: {х, у}, {х, z}, {х, t}, {у, z}, {у, t}, {z, t}
б)из перечисленных вариантов следует убрать {х, у}.Ответ: 5 вариантов
в) из а) следует убрать: {х, z}, {у, z}. Ответ: 4 варианта
г) считаем все трехэлементные подмножества:
{х, у, z}, {х, у, t}, {х, z, t}, {у, z, t} Ответ: 4 варианта

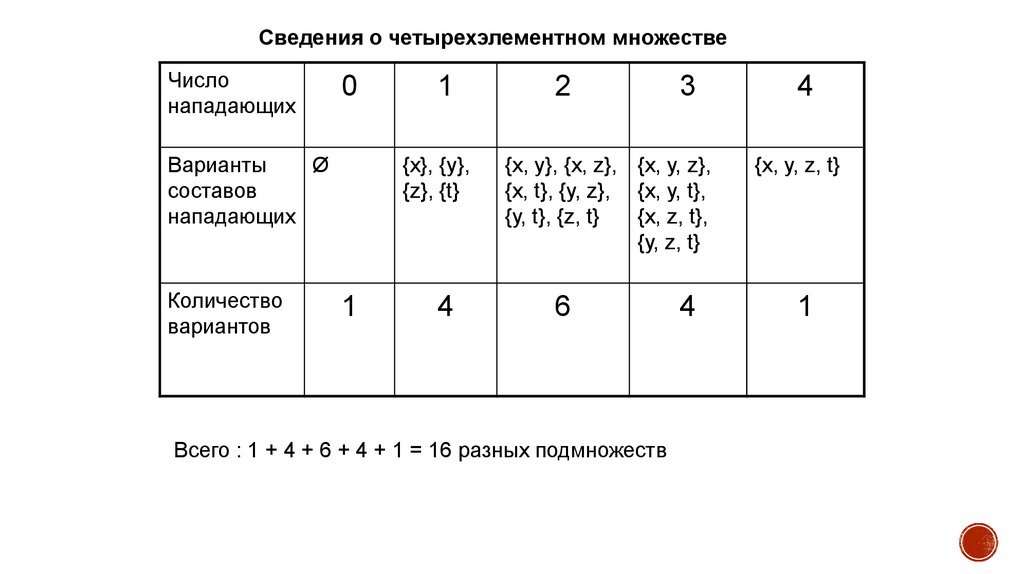
13.

Сведения о четырехэлементном множестве
Число
нападающих
0
Варианты
Ø
составов
нападающих
Количество
вариантов
1
{х}, {у},
{z}, {t}
1
4
2
3
{х, у}, {х, z}, {х, у, z},
{х, t}, {у, z}, {х, у, t},
{у, t}, {z, t}
{х, z, t},
{у, z, t}
6
Всего : 1 + 4 + 6 + 4 + 1 = 16 разных подмножеств
4
4
{х, у, z, t}
1

14. Определение

15. Примеры подмножеств

Множество учеников вашего класса является
подмножеством множества учеников вашей школы;
Множество млекопитающих является подмножеством
множества позвоночных;
Множество прямоугольников является подмножеством
множества параллелограммов;

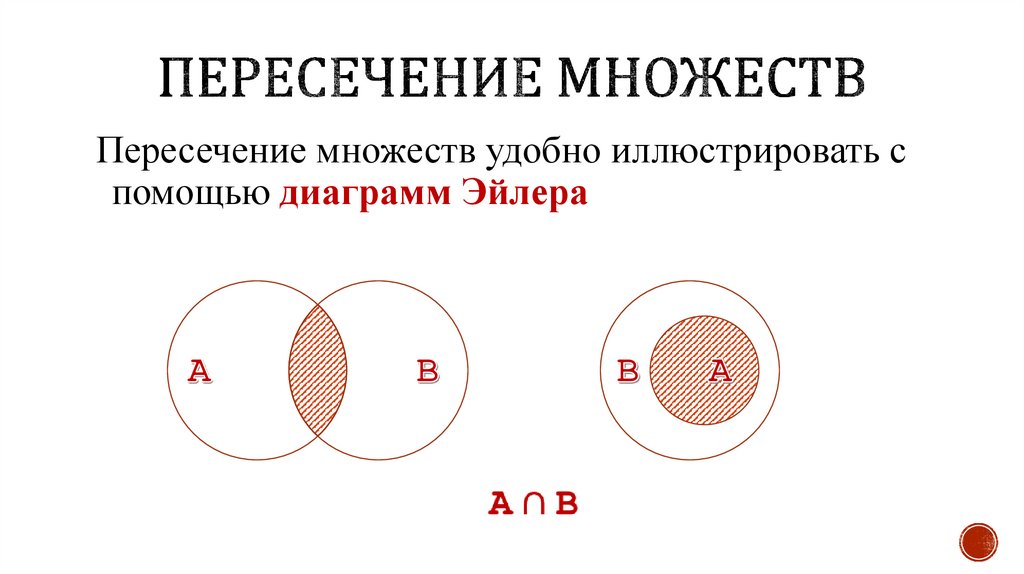
16. Диаграммы Эйлера

Для иллюстрации соотношений между множествами
пользуются схемами, которые называются
диаграммами Эйлера

17.

Изображение множеств в
виде плоских фигур очень
удобно для наглядного
объяснения различных
операций над
множествами. Обычно
множества при этом
изображают в виде
некоторых кругов. Такие
круги называют кругами
Эйлера в честь великого
немецкого математика
Леонарда Эйлера (1707 1783), который долгое
время работал в России.
А – подмножество В

18. пример

19.

Пересечение множеств
Объединение множеств
Пересечением множеств А и В
называют множество,
состоящее из всех общих
элементов множеств А и В, т.е.
из всех элементов, которые
принадлежат и множеству А, и
множеству В
Объединением множеств А и В
называют множество,
состоящее из всех элементов,
которые принадлежат хотя бы
одному из множеств – или
множеству А, или множеству В.
Обозначение:
Обозначение:
={х | х
А и х В}
= {х | х
Круги
Эйлера
{1,2,3}
{2,3,4} = {2,3}
А или х В}
Круги
Эйлера
{1,2,3}
{2,3,4} = {1,2,3,4}.

20. Определение

21. Пересечение множеств

удобно иллюстрировать с
помощью диаграмм Эйлера

22. Пример

Найдите пересечение множеств A и B, если:
1) A – множество ромбов,
B – множество прямоугольников;
2) A – множество четных чисел,
B – множество простых чисел.

23. пример

24. Определение

25. объединение множеств

Объединение множеств удобно иллюстрировать с
помощью диаграмм Эйлера

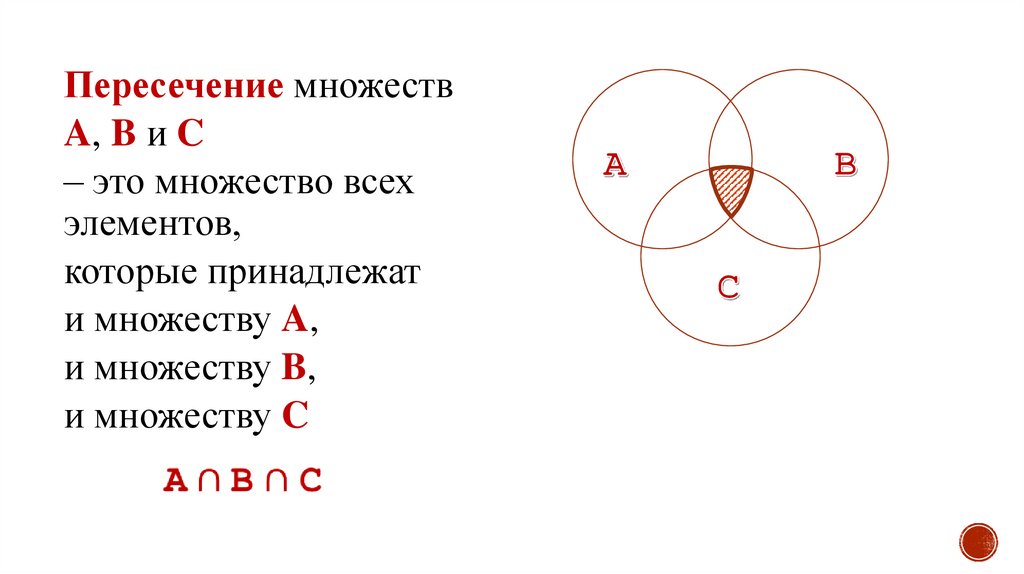
26.

Пересечение множеств
A, B и C
– это множество всех
элементов,
которые принадлежат
и множеству A,
и множеству B,
и множеству C

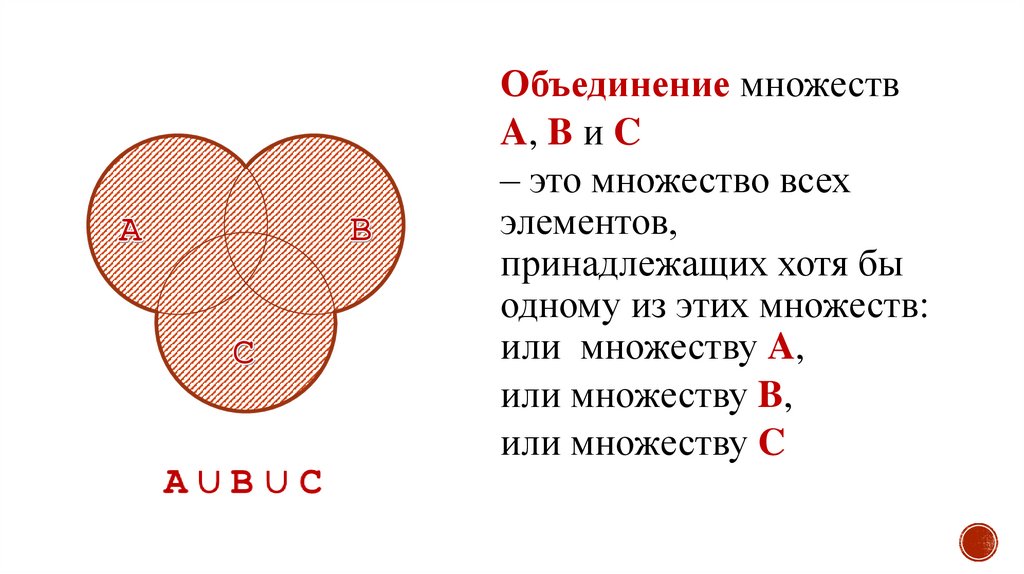
27.

Объединение множеств
A, B и C
– это множество всех
элементов,
принадлежащих хотя бы
одному из этих множеств:
или множеству A,
или множеству B,
или множеству C

28. Пример

Найдите объединение множеств A и B, если:
1) A – множество нечетных натуральных чисел,
B – множество четных натуральных чисел;
2) A – множество целых выражений,
B – множество дробных выражений.

29. пример

30.

Пример. Найти пересечение множеств А и В:
а) А = {11, 22, …, 88, 99}, В = {3, 6, 9, …}
б) А – множество различных букв, используемых в слове
«перераспределение», В – множество различных букв,
используемых в слове « реформирование»
в) А = ( 1, √10), В = N;
г) А – множество точек окружности радиуса 1 с центром в
начале координат, В – множество точек прямой у = 3х – 5.
Ответ:
а) А∩В = {33, 66, 99}
б) А∩В = {е, р, а, н, и}
в) А∩В = {2, 3}
г) А∩В = Ø

31.

Можно рассматривать пересечения не только двух
множеств, но и трех, четырех и т.д. множеств.
Пересечением множеств А, В и С называют множество,
состоящее из всех элементов, которые принадлежат и
множеству А, и множеству В, и множеству С.
Пересечение множеств А, В и С обозначают так: А∩В∩С.
Пример выполнения нескольких условий : решение
системы уравнений.

32.

Пример. Найти объединение множеств А и В.
а) А – множество делителей числа 105, В – множество
делителей числа 55;
б) А – множество цифр числа 35, в – множество цифр числа
210;
в) А = (1; √10), В = [ 2, 4];
г) А – множество точек координатной плоскости, у которых
абсцисса больше 3, В – множество точек координатной
плоскости, у которых ордината не больше 2.
Ответ:
а) АUВ = {1, 3, 5, 7, 11, 15, 21, 35, 55, 105}
б) АUВ = {0, 1, 2, 3, 4}
в) АUВ = (1,; 4]

33.

Можно рассматривать объединения не только двух, но
и трех, четырех и т.д. множеств.
Объединением множеств А, В, С называют множество,
состоящее из всех элементов, которые принадлежат
или множеству А, или множеству В, или множеству С.
Объединение множеств А, В, С обозначают так:
АUВUС
Пример: решение неравенств