Похожие презентации:
Преобразование логических выражений
1.
Если хочешь иметь досуг,не теряй времени даром.
Бенджамин Франклин
2.
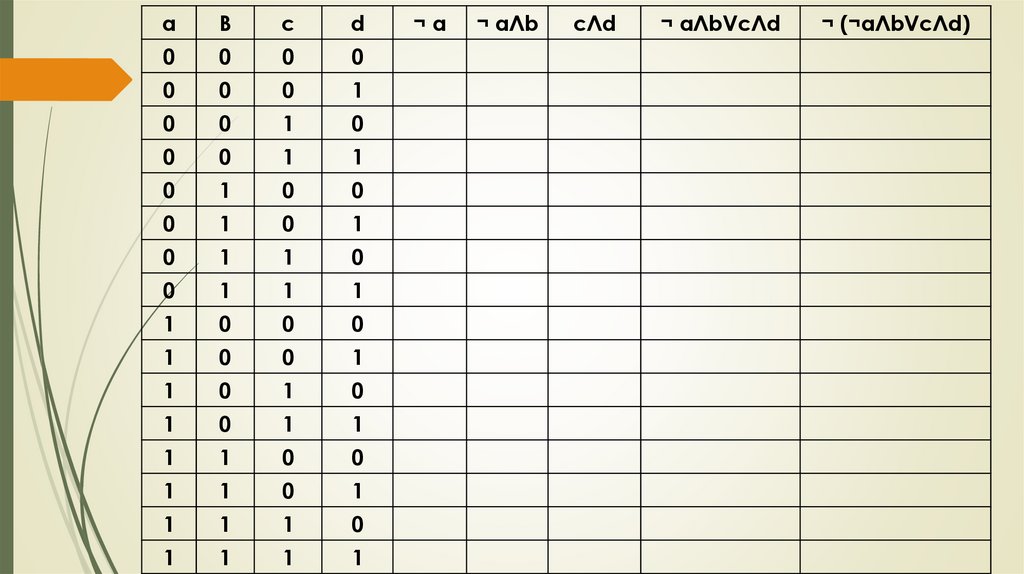
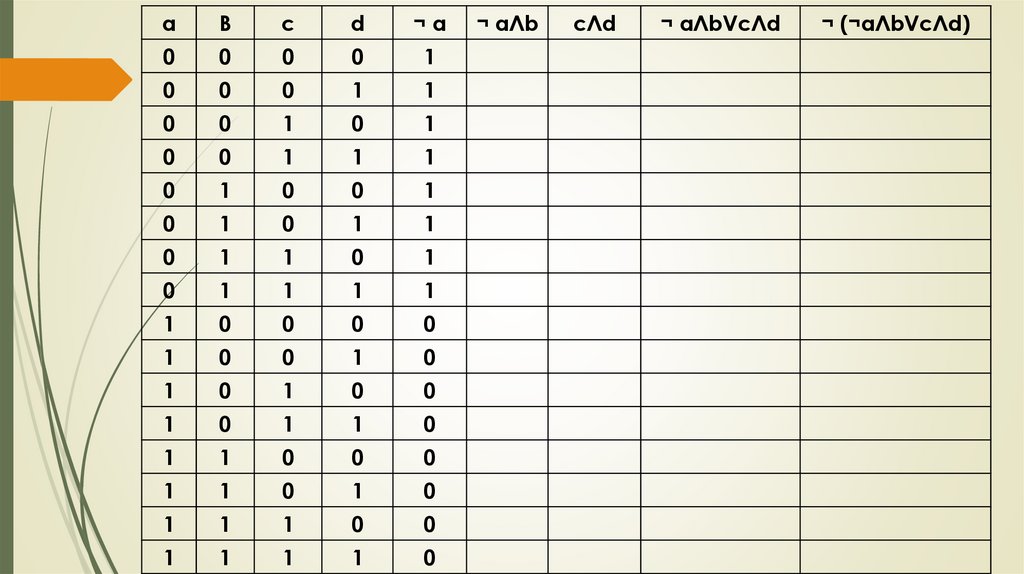
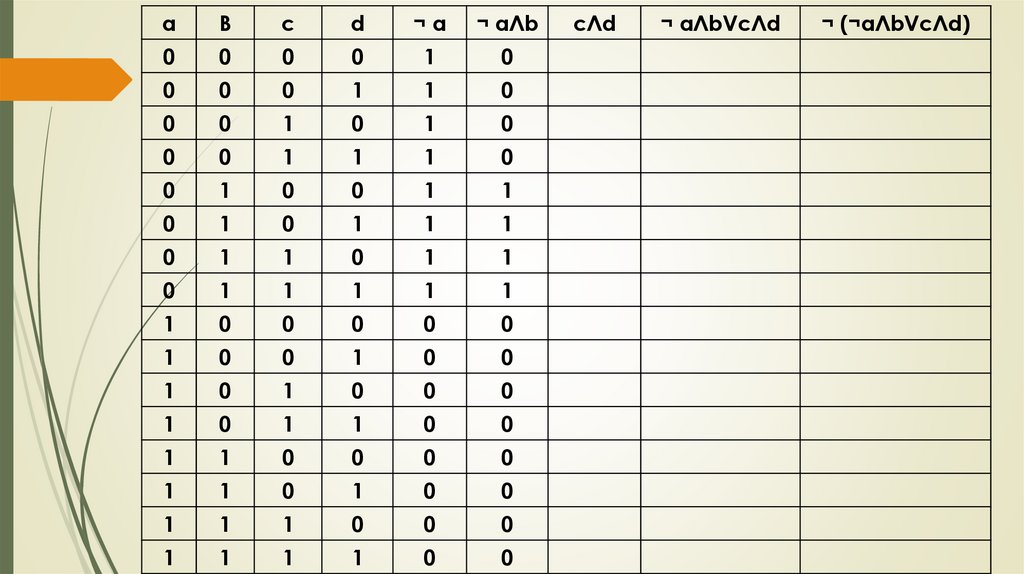
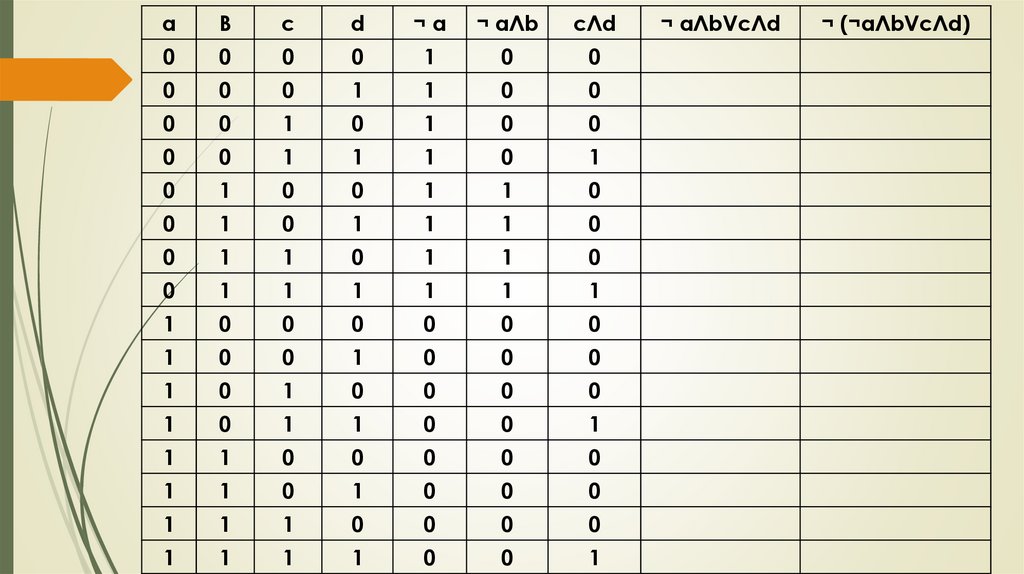
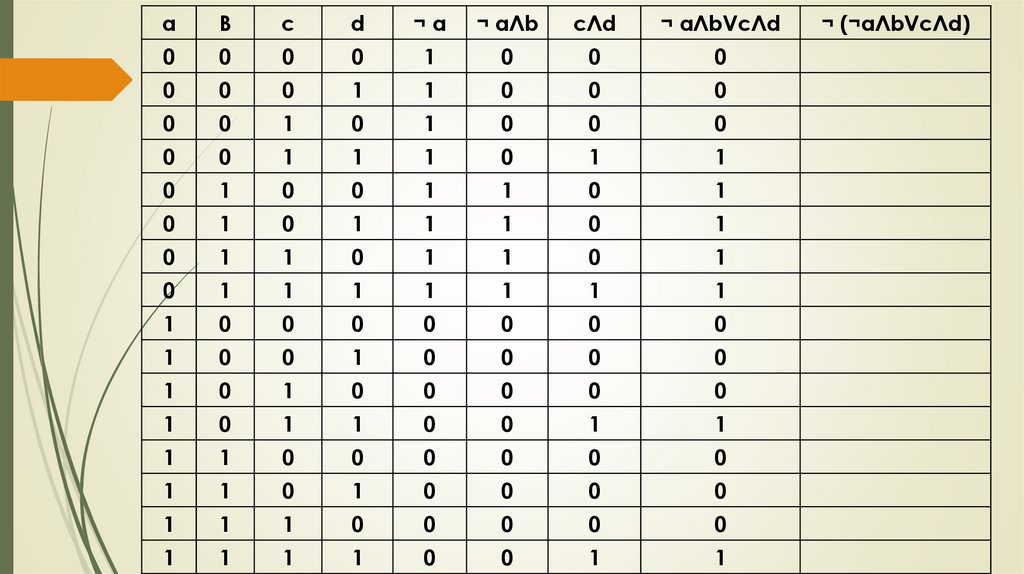
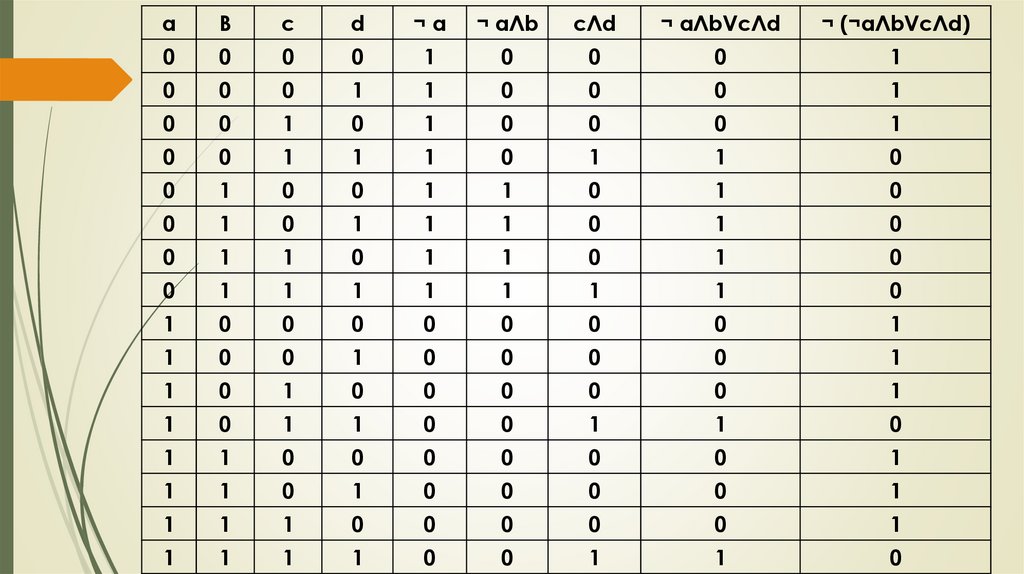
Проверка домашнего заданияПостройте таблицу истинности логического выражения:
¬ (¬ a Л b V c Л d)
3.
aB
c
d
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
¬a
¬ aЛb
cЛd
¬ aЛbVcЛd
¬ (¬aЛbVcЛd)
4.
aB
c
d
¬a
0
0
0
0
1
0
0
0
1
1
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
¬ aЛb
cЛd
¬ aЛbVcЛd
¬ (¬aЛbVcЛd)
5.
aB
c
d
¬a
¬ aЛb
0
0
0
0
1
0
0
0
0
1
1
0
0
0
1
0
1
0
0
0
1
1
1
0
0
1
0
0
1
1
0
1
0
1
1
1
0
1
1
0
1
1
0
1
1
1
1
1
1
0
0
0
0
0
1
0
0
1
0
0
1
0
1
0
0
0
1
0
1
1
0
0
1
1
0
0
0
0
1
1
0
1
0
0
1
1
1
0
0
0
1
1
1
1
0
0
cЛd
¬ aЛbVcЛd
¬ (¬aЛbVcЛd)
6.
aB
c
d
¬a
¬ aЛb
cЛd
0
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
1
0
1
0
1
0
0
1
1
0
0
1
0
1
1
1
0
0
1
1
0
1
1
0
0
1
1
1
1
1
1
1
0
0
0
0
0
0
1
0
0
1
0
0
0
1
0
1
0
0
0
0
1
0
1
1
0
0
1
1
1
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
0
0
0
0
1
1
1
1
0
0
1
¬ aЛbVcЛd
¬ (¬aЛbVcЛd)
7.
aB
c
d
¬a
¬ aЛb
cЛd
¬ aЛbVcЛd
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
1
1
0
1
0
0
1
1
0
1
0
1
0
1
1
1
0
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
0
0
0
0
0
1
1
0
1
0
0
0
0
1
1
1
0
0
0
0
0
1
1
1
1
0
0
1
1
¬ (¬aЛbVcЛd)
8.
aB
c
d
¬a
¬ aЛb
cЛd
¬ aЛbVcЛd
¬ (¬aЛbVcЛd)
0
0
0
0
1
0
0
0
1
0
0
0
1
1
0
0
0
1
0
0
1
0
1
0
0
0
1
0
0
1
1
1
0
1
1
0
0
1
0
0
1
1
0
1
0
0
1
0
1
1
1
0
1
0
0
1
1
0
1
1
0
1
0
0
1
1
1
1
1
1
1
0
1
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
1
0
0
0
0
0
1
1
0
1
1
0
0
1
1
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
0
1
1
1
1
1
0
0
1
1
0
9.
Критерии оценивания:«5» – все выполнено верно без ошибок,
«4» – допущены ошибки в 1-3 строках,
«3» - допущены ошибки в 4-6 строках,
«не справился с заданием» - допущены
ошибки в 7 и более строках.
10.
Способ определения истинности логическоговыражения путем построения его таблицы
истинности становится неудобным при увеличении
количества логических переменных, т. к. за счет
существенного увеличения числа строк таблицы
становятся громоздкими.
В таких случаях выполняются преобразования
логических выражений в равносильные. Для
этого используют законы алгебры логики.
11.
Преобразование логическихвыражений.
Цели урока:
Научиться
преобразовывать
логические
выражения в равносильные с помощью законов
алгебры логики.
Вспомнить построение таблицы истинности
логического выражения средствами MS Excel
12.
Видео фрагмент урока сдистанционного образовательного
ресурса РЭШ
13.
Решение задач на преобразованиелогических выражений
Стр. 190 №1(а,в)
№2 (в)
№3 (г)
Дополнительное задание: №2 (е); №3 (в)
14.
Домашнее задание:П. 21 прочитать, №1 (б,г), №2(и,д), №3(б)
Дополнительное домашнее задание:
№3(е)+задание на листах
15.
16.
Практическая работаУпростить логическое выражение,
полученный результат проверить с помощью
построения таблицы истинности в MS Excel.
¬А ¬ С А B ¬А С А ¬В











 Информатика
Информатика








