Сложность алгоритмов

1.

Сложность алгоритмов
Нотация Big O

2.

Определение
• Сложность алгоритма - это количественная
характеристика, которая говорит о том, сколько времени,
либо какой объём памяти потребуется для выполнения
алгоритма.
• Развитие технологий привело к тому, что память перестала быть
критическим ресурсом. Поэтому когда говорят об анализе
сложности алгоритма, обычно подразумевают то, насколько
быстро он работает.
• Также, выполнения алгоритма зависит от того, на каком
устройстве его запустить. Один и тот же алгоритм запущенный на
разных устройствах выполняется за разное время. Поэтому было
предложено измерять сложность алгоритмов в количестве
действий, которое необходимо совершить для выполнения
алгоритма.

3.

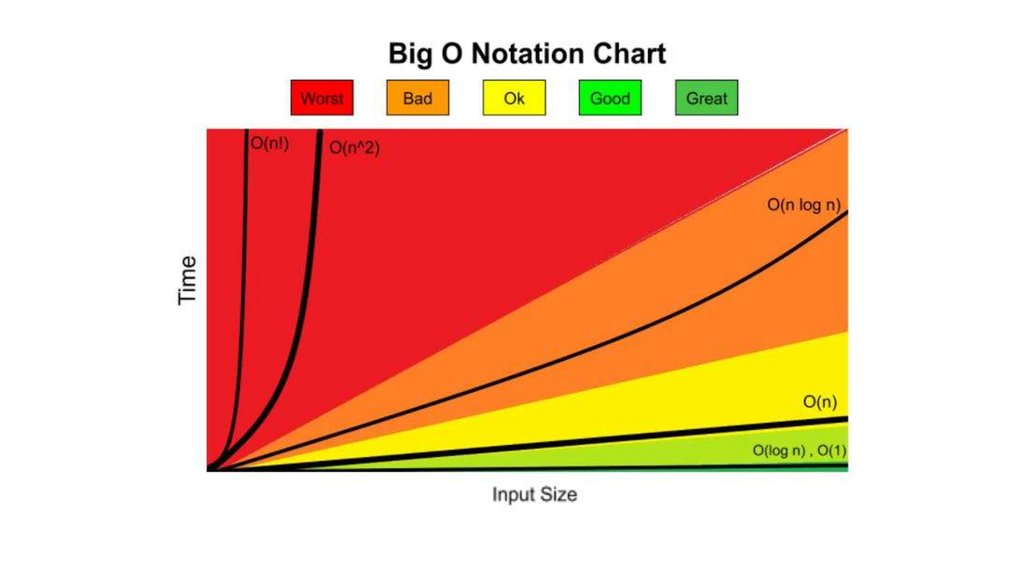
Нотация Big O
• Любой алгоритм включает в себя определённое количество
шагов и не важно на каком устройстве он будет запущен,
количество шагов останется неизменным. Эту идею принято
представлять в виде Big O (или О-нотации).
• Big O показывает то, как сложность алгоритма растёт с
увеличением входных данных. При этом она всегда показывает
худший вариант развития событий - верхнюю границу.

4.

Зачем изучать Big O
• Концепцию Big O необходимо понимать, чтобы уметь видеть и
исправлять неоптимальный код.
• Ни один серьёзный проект, как ни одно серьёзное
собеседование, не могут обойтись без вопросов о Big O.
• Непонимание Big O ведёт к серьёзной потере
производительности ваших алгоритмов.

5.

Константная сложность O(1)
• Означает, что вычислительная сложность алгоритма не зависит от
входных данных. Однако, это не значит, что алгоритм
выполняется за одну операцию или требует очень мало времени.
Это означает, что время не зависит от входных данных.
• Пример 1: получение данных по индексу/ключу
• Пример 2: сложение двух чисел
• Пример 3: нахождение размера контейнера (если класс
контейнера изначально содержит поле размера)
• Пример 4: узнайте, четное или нечетное число.

6.

Линейная сложность O(N)
• Означает, что сложность алгоритма линейно растёт с
увеличением входных данных.
• Другими словами, удвоение размера входных данных удвоит и
необходимое время для выполнения алгоритма.
• Такие алгоритмы легко узнать по наличию цикла по каждому
элементу массива.
• Пример 1: распечатайте все значения в списке.
• Пример 2: нахождение максимума в несортированном списке.
• Пример 3: нахождение суммы списка.
• Пример 4: нахождение среднего значения в списке.
• Пример 5: найдите данный элемент в коллекции.

7.

2
Квадратическая сложность O(N )
• Означает, что удвоение размера входных данных увеличивает
время выполнения в 4 раза.
• Например, при увеличении данных в 10 раз, количество
операций (и время выполнения) увеличится примерно в 100 раз.
• Если алгоритм имеет квадратичную сложность, то это повод
пересмотреть необходимость использования данного алгоритма.
Но иногда этого не избежать.
• Такие алгоритмы легко узнать по вложенным циклам.
• Пример 1: пузырьковая сортировка.
• Пример 2: проверьте, есть ли в коллекции повторяющиеся
значения (неоптимизированное решение).

8.

Логарифмическая сложность O(log n)
• Означает, что сложность алгоритма растёт логарифмически с
увеличением входных данных. Другими словами это такой
алгоритм, где на каждой итерации берётся половина элементов.
• К алгоритмам с такой сложностью относятся алгоритмы типа
“Разделяй и Властвуй” (Divide and Conquer), например бинарный
поиск.
• Пример: поиск слова в физическом словаре (открывая словарь с
середины).

9.

Линейноарифметическая O(n * log n)
• Означает, что удвоение размера входных данных увеличит время
выполнения чуть более, чем вдвое.
• Пример: сортировка слиянием.

10.

n
Экспоненциальное время O(2 )
• Экспоненциальное (основание 2) время выполнения означает,
что вычисления, выполняемые алгоритмом, удваиваются каждый
раз по мере увеличения входных данных.
• Пример: Фибоначчи, задача коммивояжера с использованием
динамического программирования

11.

Факторное время O(N!)
• 5 элементов = 5*4*3*2*1 = 120 действий
• Пример: все перестановки букв в слове

12.

13.

14.

Суммируем
• Получение элемента коллекции это O(1). Будь то получение по
индексу в массиве, или по ключу в словаре в нотации Big O это
будет O(1)
• Перебор коллекции это O(n)
• Вложенные циклы по той же коллекции это O(n^2)
• Разделяй и властвуй (Divide and Conquer) всегда O(log n)
• Итерации которые используют Divide and Conquer это O(n log n)

15.

Структуры данных

16.

Сортировка

17.

Поиск

18.

Кучи

19.

Представление графов