Похожие презентации:
Фигура и размеры Земли. Понятие о картографических проекциях
1.
НАО Кар ТУКафедра МД и Г
Автор: доцент, к.т.н. Старостина О.В.
Фигура и размеры земли
2. План лекции:
1) Фигура Земли;2) Понятие о
картографических проекциях;
3) Классификация по виду
вспомогательной сетки;
3. Фигура Земли
Необходимостьприменения
картографических
проекций
возникает во всех случаях, когда
требуется графически изобразить на
плоскости в виде карты или
аналитически выразить с помощью
плоских
координат
абсолютное
положение точек земной поверхности.
4.
В первом приближении фигуруЗемли можно принимать за шар.
Для
приближенных
суждений
можно принять радиус земного шара
равным R = 6400 км.
При
изображении
земной
поверхности как шаровой, шар
обыкновенно берется равновеликим
по поверхности с земным сфероидом.
5.
Условие равенства поверхностейопределяет
радиус
R
шара
уравнением:
R
2
M
N
cos
d
0
6.
При изображении части земнойповерхности удобно брать радиус
шара равным среднему радиусу Rcp
кривизны
в
средней
точке
изображаемой области:
Rср M N
7.
В этих формулах М и N —радиусы
кривизны
земного
сфероида
по
главным
нормальным сечениям в данной
точке:
М
—
наименьший
радиус
кривизны, по меридиональному
сечению;
8.
N—
наибольший
радиус
кривизны, по сечению, перпендикулярному
меридиану,
равный
длине нормали от поверхности
сфероида до оси вращения.
9. Эллипсоид Ф. Н. Красовского
Большая полуось а = 6378245,0000 м;сжатие a b
1
= 0,00335233;
a
298.3
малая полуось в = 6356863,0188 м.
10. Понятие о картографических проекциях
Математическаякартография
изучает
вопросы
изображения
математической поверхности Земли,
Луны, планет и звездного неба на
плоскости.
При создании карт прибегают к
картографическим проекциям, т. е. к
отображению
поверхности
на
плоскости.
11.
В основу такого изображенияположены
линии
системы
географических координат.
Изображаемая поверхность в
одних частях искусственно как бы
растягивается, а в других —
сжимается.
12.
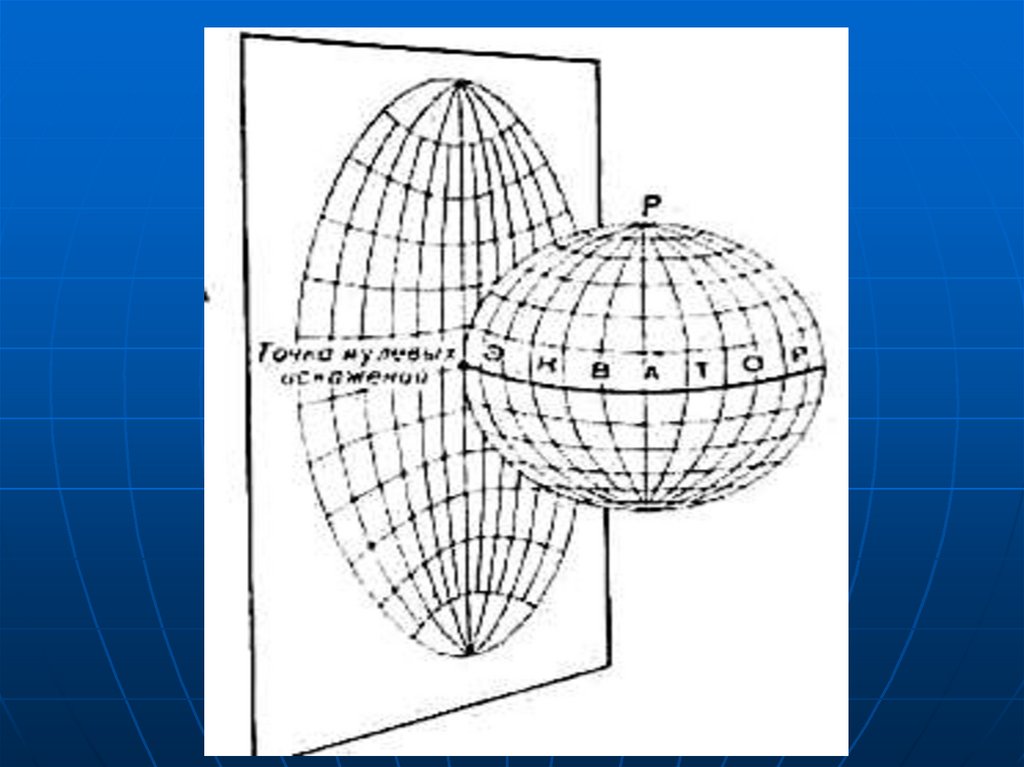
Для того чтобы проводить накарте точные измерения, нужно
знать картографическую проекцию,
в которой она составлена, и закон
распределения искажений.
13. Понятие о картографических проекциях
Основные задачи математическойкартографии:
1) изучение картографических
проекций, их свойств, взаимосвязей
и целесообразности применения на
практике;
14.
2)совершенствование
имеющихся
картографических
проекций и разработка новых (в
соответствии с требованиями науки
и производства) ;
3) совершенствование методов
изысканий новых картографических
проекций;
15.
4)разработка
новых
математических элементов карт
(рамок, разграфки и номенклатуры,
необходимых для многолистных
карт);
5) изучение способов и средств
измерений
по
картам
(с
использованием картографических
сеток);
16.
6) изучение и решение задачматематического
характера,
возникающих при составлении
карт
(например,
разработка
технических
средств,
облегчающих
измерения
по
картам, и др.).
17. Понятие о картографических проекциях
Картографируемые поверхностипринимают (для Земли) за шар или
за эллипсоид вращения, малая ось
которого совпадает с осью вращения
Земли.
18.
Картографическаяпроекция
определяет переход от поверхности
эллипсоида (или шара) к плоскости,
а также закон распределения
искажений, возникающих при этом
на карте.
Поверхность эллипсоида нельзя
развернуть
в
плоскость
с
сохранением
подобия
всех
очертаний.
19.
Еслиповерхность
глобуса
(модель
земного
эллипсоида),
разрезанную
на
полоски
по
меридианам
(или
параллелям),
развернуть
в
плоскость,
в
картографическом
изображении
произойдут
разрывы
или
перекрытия, и с удалением от
экватора
(или
от
среднего
меридиана) они будут возрастать.
20.
Поверхность глобуса, разрезанная попараллелям на пояса
21.
Карта мира, полученнаярастяжением поясов
22.
При переходе от физическойповерхности
Земли
к
ее
отображению
на
плоскости
выполняют две операции:
во-первых, проектирование земной
поверхности с ее сложным рельефом
на поверхность земного эллипсоида,
размеры
которого
установлены
посредством
геодезических и
астрономических измерений;
23.
во-вторых,изображение
поверхности
эллипсоида
на
плоскости посредством одной из
картографических проекций.
24. Классификация картографических проекций
Способизображения
поверхности земного эллипсоида или
шара на плоскости называется
картографической проекцией
25.
Изображение меридианов ипараллелей земного эллипсоида на
плоскости, выполненное в той или
иной
проекции,
называется
картографической сеткой.
26.
Такиепроекции,
которые
сохраняли
бы
подобие
и
пропорциональность всех частей
земной поверхности, может иметь
место только на модели эллипсоида.
Вместе с тем есть проекции,
свободные от искажения углов или
от искажения площадей.
27. Картографические проекции обычно различают:
1) по характеру искажений;2) по виду картографической
сетки, с помощью которой сеть
меридианов
и
параллелей
с
эллипсоида переносят на плоскость;
3) по территориальному охвату.
28. По характеру искажений проекции делятся на:
равноугольные,равновеликие и
произвольные .
29.
Равноугольные(конформные)
проекции сохраняют величину углов
и формы бесконечно малых фигур.
Масштаб длин в каждой точке
постоянен по всем направлениям и
зависит только от положения точки.
Эллипсы искажений выражаются
окружностями различных радиусов.
30.
Равноугольная проекция(стереографическая)
31. Равноугольная цилиндрическая проекция (Меркатора)
32.
В равноугольных проекциях накарте отсутствуют искажения углов, в
них
не
искажаются
формы
бесконечно малых фигур, а масштаб
длин в любой точке остается
одинаковым по всем направлениям,
но в этих проекциях карты больших
территорий
отличаются
значительными
искажениями
площадей.
33.
В равновеликих проекциях неискажаются площади. В этих
проекциях
площади
эллипсов
искажений равны.
Увеличение масштаба длин по
одной оси эллипса искажений
компенсируется
уменьшением
масштаба длин по другой оси, что
вызывает сильное искажение форм.
34. Равновеликая проекция
35.
Равновеликие, это проекции вкоторых
на
карте
отсутствуют
искажения площадей, следовательно,
соотношения площадей территорий
передаются правильно.
В этих проекциях карты больших
территорий отличаются значительными искажениями углов и форм.
36. Равновеликая цилиндрическая проекция
37. Задание СРС 3:
1. Когда применяется шаровая модель Земли?2.
Какие
параметры
определяют
сфероидическую модель?
3. Какие радиусы кривизны эллипсоида
вращения
используются
при
картографировании?
4. Чем отличаются сферические долготы и
широты от геодезических долгот и широт?
5.
Что
понимается
под
термином
«географическая сетка»?
38. Произвольные проекции
Произвольные проекции - этопроекции в которых на карте в
любых
соотношениях
имеются
искажения и углов, и площадей.
39. Запомните
Проекций, совершеннолишенных
искажений длин,
не существует.
40.
Существует множество проекций,которые не являются:
ни равноугольными,
ни равновеликими, —
их называют произвольными.
41.
Но нет и не может бытьпроекции,
которая
была
бы
одновременно равноугольной и
равновеликой
эти
качества
исключают друг друга.
Вообще говоря, чем больше
искажения углов, тем меньше
искажения площадей, и наоборот.
42.
Среди произвольных проекцийвыделяют равнопромежуточные,
во всех точках которых масштаб по
одному из направлений, например
по меридианам или параллелям,
постоянен и равен главному.
По
своим
свойствам
произвольные
проекции
лежат
между
равноугольными
и
равновеликими.
43.
Равнопромежуточнаяцилиндрическая проекция
44.
Вравнопромежуточных
проекциях, масштаб длин по одному
из главных направлений сохраняется
постоянным.
В них искажения углов
и
искажения
площадей как бы
уравновешены.
45.
В картографической практикераспространена
классификация
проекций по виду вспомогательной
геометрической
поверхности,
которая может быть использована
при их построении.
46.
С этой точки зрения выделяютпроекции:
цилиндрические,
когда
вспомогательной
поверхностью
служит
боковая
поверхность
цилиндра,
касательного
к
эллипсоиду
или
секущего
эллипсоид; после чего последний
разрезается по образующей и
развертывается в плоскость;
47.
конические,когда
вспомогательной
поверхностью
является
боковая
поверхность
касательного или секущего конуса;
азимутальные,
когда
вспомогательная поверхность —
касательная или секущая плоскость.
48.
Геометрическоепостроение
названных проекций отличается
большой наглядностью.
Для простоты рассуждения
вместо эллипсоида воспользуемся
шаром.
49. Классификация по виду вспомогательной сетки
50. Классификация по ориентировке вспомогательной поверхности
Рассмотренные проекции, припостроении которых оси цилиндра
и конуса совмещались с полярной
осью земного шара, а плоскость
размещалась касательно в точке
полюса, называются
н о р м а л ь н ы м и.
51.
Таким образом, в нормальнойсетке
любой
цилиндрической
проекции параллели и меридианы
образуются двумя семействами
взаимно
перпендикулярных
прямых линий, причем меридианы
всегда являются равноотстоящими.
52.
Наряду с нормальными сетками вкартографии широко используют
для
цилиндрических
и
азимутальных проекций другие
ориентировки
цилиндра
и
плоскости: поперечные, когда ось
цилиндра лежит в плоскости
экватора , а плоскость касается
шара в одной из точек экватора;
53.
Косые проекции, когда осьцилиндра или конуса образует с
полярной осью острый угол, а
плоскость касается шара в какой-либо
точке между полюсом и экватором.
Нормальную
азимутальную
проекцию часто называют полярной, а
поперечную азимутальную проекцию
— экваториальной.
54. Азимутальные проекции
55.
56.
57.
58. Цилиндрические проекции (поперечная и косая)
59. Равнопромежуточная коническая проекция
60.
Повиду
нормальной
картографической сетки прежде
всего выделяют проекции, в которых
параллели
изображаются
на
плоскости линиями постоянной
кривизны, т. е. прямыми линиями,
окружностями или их дугами.
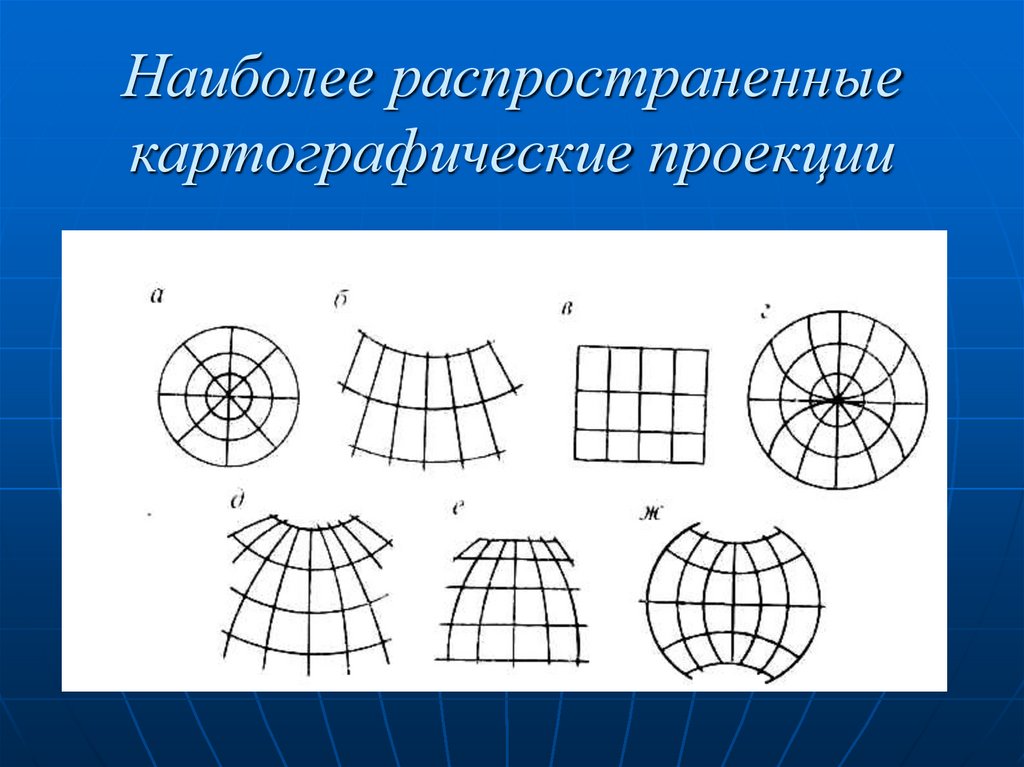
61.
Наиболее распространенныекартографические проекции
62. азимутальные ( а)
Вкоторых
параллели
изображаются
концентрическими
окружностями, а меридианы —
прямыми, исходящими из общего
центра параллелей под углами,
равными разности их долгот;
63. конические (б)
которыхпараллели
изображаются
дугами
концентрических окружностей, а
меридианы
—
прямыми,
расходящимися из общего центра
параллелей
под
углами,
пропорциональными разности их
долгот.
В
64. конические (б)
Известны также обобщенныеконические проекции, которые
отличаются от конических тем, что
угол между прямыми меридианами
есть более сложная функция
долготы;
65. цилиндрические (в)
Вкоторых
меридианы
изображаются
равноотстоящими
параллельными
прямыми,
а
параллели — перпендикулярными
к ним прямыми, в общем случае не
равноотстоящими.
66. цилиндрические (в)
Известныобобщенные
цилиндрические
проекции,
в
которых
расстояния
между
меридианами есть более сложная
функция долготы.
67.
Условныминазываются
проекции, при построении которых
не прибегают к использованию
вспомогательных геометрических
поверхностей.
Сеть меридианов и параллелей
строят по какому-нибудь заранее
заданному условию.
68.
Средиусловных
проекций
можно
выделить
псевдоцилиндрические
и
псевдоконические
проекции,
сохраняющие
от
исходных
цилиндрических и конических
проекций вид параллелей.
69.
В этих проекциях средниймеридиан
прямая
линия,
остальные меридианы - кривые
линии.
Условные проекции получили
весьма широкое применение.
70. псевдоазимутальные (г)
Вкоторых
параллели
изображаются
концентрическими
окружностями,
меридианы
—
кривыми, сходящимися в точке
полюса;
средний
меридиан —
прямой.
71. псевдоконические (д)
которыхпараллели
изображаются
дугами
концентрических
окружностей,
средний меридиан — прямой,
проходящей через их общий центр, а
остальные меридианы — кривыми;
В
72. псевдоцилиндрические (е),
Вкоторых
параллели
изображаются
параллельными
прямыми, средний меридиан —
прямая,
перпендикулярная
к
параллелям, а остальные меридианы
— кривые или прямые, наклоненные
к параллелям;
73. поликонические (ж),
Вкоторых
параллели
изображаются
дугами
эксцентрических окружностей с
радиусами тем большими, чем
меньше их широта, средний
меридиан — прямой, на которой
расположены
центры
всех
параллелей, остальные меридианы
— кривые.
74.
Принцип построения поликонической проекции. а — положение конусов; б — полосы; в— развертка.
Принцип построения поликонической проекции.
а — положение конусов; б — полосы;
в — развертка.
75.
Поликоническими называютсяпроекции,
в
которых
сеть
меридианов и параллелей с
поверхности
эллипсоида
переносится
на
боковые
поверхности нескольких конусов,
каждый из которых разрезается, по
образующей и развертывается в
плоскость.
76.
Впоперечных
и
косых
цилиндрических и азимутальных
проекциях сетки меридианов и
параллелей образуются кривыми
линиями и потому , классификация
проекций по виду меридианов и
параллелей
производится
применительно
к
нормальным
сеткам.
77.
Кромеперечисленных
существуют проекции, в которых
параллели изображаются линиями
переменной кривизны.
Иногда проекции, не входящие
ни в один из этих классов, называют
условными.
78.
Иногдаособо
выделяют
круговые проекции, в которых и
меридианы,
и
параллели
изображаются окружностями или
их дугами, однако их можно
рассматривать и как частный
случай поликонических проекций.
79.
Производныепроекции,
получают преобразованием одной
или нескольких ранее известных
проекций путем комбинирования и
обобщения их уравнений,
введением
в
уравнения
дополнительных постоянных и т. п.
80.
Схема многогранной проекции ирасположение листов карт
81.
По особенностям использованияразличают проекции:
-многогранные,
в
которых
параметры проекции подобраны
для каждого листа или группы
листов многолистной карты;
82.
-многополосные,в
которых
параметры подобраны для каждой
отдельной полосы, на которые при
отображении
разбивается
поверхность эллипсоида или шара.
83. Задание СРС:
1. Что понимается под прямой задачейматематической картографии? Какие можно
указать прямые способы получения проекций?
2. Где располагают центр проектирования
(точку глаза) и плоскость проектирования при
перспективном проектировании шара на
плоскость?
3. Как изменяются свойства перспективных
азимутальных
проекций
с
изменением
положения центра проектирования?
84. Задание СРС:
4. Какими отличительными свойствамиобладают гномоническая, стереографическая и
ортографическая перспективные азимутальные
проекции?
5. С какой целью строят многополосные
проекции? Какими линиями ограничивают эти
полосы?
Назовите
известные
вам
многополосные проекции.
6. Какие
проекции
называют
многогранными? Какие у них достоинства и
какой недостаток?
85.
Среди азимутальных проекцийвыделяют перспективные проекции,
получаемые
проектированием
поверхности шара на плоскость по
закону перспективы посредством
лучей из точки зрения,
86.
располагаемойна
прямой,
проходящей через центр шара и
перпендикулярной
плоскости
касания (картинной плоскости).
87.
88. В частности, различают перспективные проекции:
—центральные(гномонические),
когда точка зрения находится в
центре шара, в этой проекции все
большие круги шара изображаются
прямыми линиями;
89.
— стереографические, когда точказрения
располагается
на
поверхности шара и диаметрально
противоположна точке касания
картинной
плоскости;
стереографическая
проекция
равноугольна; любая окружность на
поверхности шара изображается в
этой проекции также окружностью;
90.
—ортографические,когда точка
зрения удалена в бесконечность
и проектирование производится
пучкам параллельных лучей ( в
этой проекции мы практически
видим поверхность луны);
91.
—внешние
центр
проектирования
лежит
вне
поверхности Земли, но на
конечном расстоянии.
92.
Практическое применение имеютдве первые.
Если шар проектируется изнутри
—
получают
перспективные
проекции с негативным изображением, при проектировании снаружи,
когда из центра проектирования
видна внешняя поверхность шара,
получают проекции с позитивным
изображением.
93. Эмблема Объединенных наций – равнопромежуточная азимутальная проекция
94.
Поперечныеи
косые
конические
проекции
в
картографической
практике
употребляются весьма редко.
95.
Потерриториальному
охвату
выделяются картографические проекции:
- для карт мира;
- полушарий материков и океанов;
- карт отдельных государств и их
частей.
По этому принципу построены
таблицы
определители
картографических проекций.
96.
Азимутальные проекции чащевсего применяются для территорий,
протяжённость которых по широте
и долготе примерно одинакова:
-полярные азимутальные - для
северного и южного полушарий;
-экваториальные
для
восточного и западного полушарий
и для карт Африки;
-горизонтальные - для карт Азии,
Австралии и т.п.
97.
В нормальных цилиндрическихпроекциях строятся мировые и
морские навигационные карты.
Азимутальным, коническим и
цилиндрическим
проекциям
свойственны
определенные
системы
распределения
искажений.
98.
В них все искажения являютсяфункцией лишь одной координаты
—
широты
или
зенитного
расстояния.
Поэтому
изоколы
в
этих
проекциях
совпадают
с
альмукантаратами, в нормальной
ориентировке — с параллелями.
99.
Есливспомогательные
поверхности проекций касательны к
эллипсоиду или шару, то искажения
на
картах
нарастают
по
направлениям от мест касания.
100.
Так, в азимутальных проекцияхискажения
нарастают
в
направлениях от точки нулевых
искажений, в конических — в
направлениях от главной параллели,
в цилиндрических—в направлениях
от
экватора
в
нормальной
ориентировке и в направлениях от
дуги касания
101.
В косых и поперечных проекцияхкартографические сетки отличаются
от сетки нормальных проекций.
В этих проекциях с нормальной
сеткой схожи сетки вертикалов и
альмукантаратов.
102.
Вертикал (от лат. verticalis —oтвесный), большой круг небесной
сферы, проходящий через зенит и
данную точку на сфере.
Вертикал, проходящий через точки
севера и юга, называется небесным
меридианом, через точки запада и
востока — первым вертикалом.
103.
Альмукантарат — (Almacantar)малый круг небесной сферы,
параллельный
истинному
горизонту наблюдателя.
А., проходящий через данное
светило на сфере, называется А.
данного светила.
104.
Вертикалы и альмукантаратыможно
рассматривать
как
смещенные меридианы и параллели,
получившиеся после перемещения
географического
полюса
в
положение Q (рисунок), которое
показано в косой ориентировке.
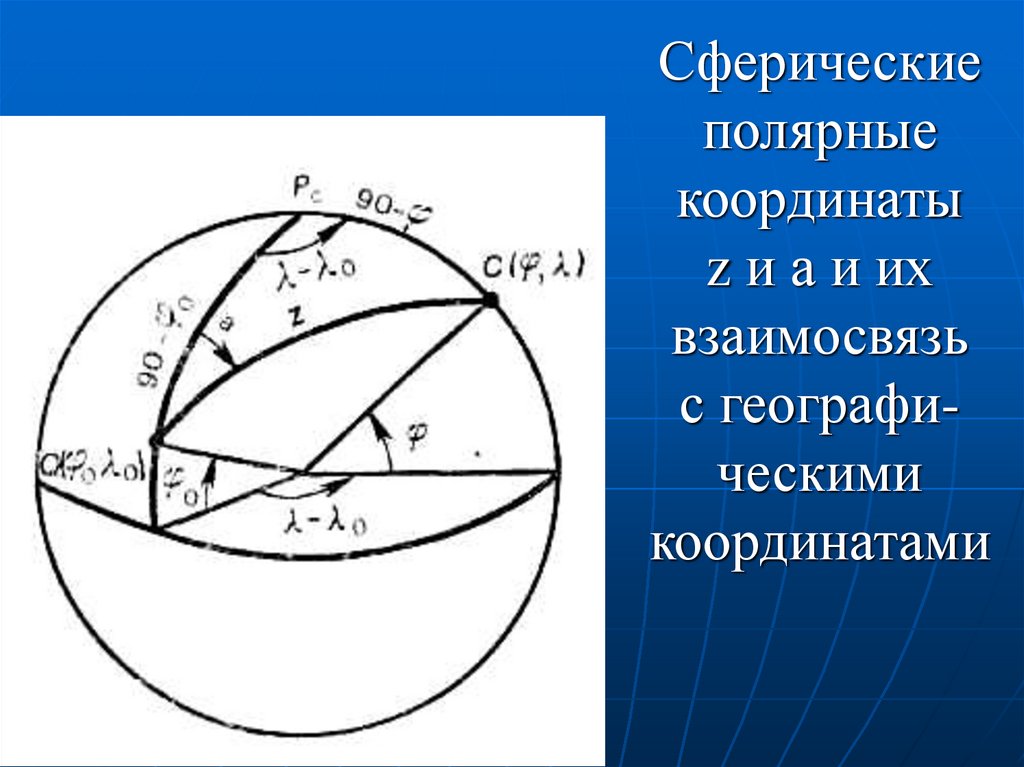
105.
Сферическиеполярные
координаты
z и а и их
взаимосвязь
с географическими
координатами
106.
Положениеальмукантарата
определяется зенитным расстоянием
z, отсчитываемым от полюса Q до
текущей точки С.
Вертикалы — линии, для которых
а = const.
Альмукантараты — линии, для
которых
z = const.
107.
Впоперечной
ориентировке
полюс Q лежит на экваторе, а в
нормальной
—
совпадает
с
географическим полюсом.
108.
Положениевертикала
определяется
азимутом
и
двугранным
углом
между
плоскостью меридиана полюса Q и
плоскостью, проведенной через
нормаль в точке Q в направлении на
секущую точку С (см. рисунок).
109.
Послеперемещения
на
поверхности относимости полюса Q в
географический полюс:
-вертикалы
совпадают
с
меридианами;
-альмукантараты
—
с
параллелями.
110.
В случае шара вертикалы — дугибольших кругов, альмукантараты—
дуги малых кругов. Величины z, а
называют полярными сферическими
координатами.
Переход от широт, долгот
к
азимутам а и зенитным расстояниям z
осуществляется
по
формулам
сферической тригонометрии:
111.
где о, о — широта и долготаполюса Q.
В
случае
поперечной
ориентировки
формулы
упрощаются.
112.
Искажения в картографическихпроекциях
В результате растяжений или
сжатий
в
картографическом
изображении возникают искажения
в длинах, площадях, формах и
углах.
113.
Линииили
точки
касания
поверхности
эллипсоида
с
плоскостью, изображаемые без
искажений,
принято
называть
линиями или точками нулевых
искажений.
114.
Масштаб изображения на этихлиниях или в точках - главным
масштабом.
Масштабы в других местах карты
называются частными.
115.
Масштаб карты — степеньуменьшения объектов на карте относительно их размеров на земной
поверхности
(точнее,
на
поверхности эллипсоида).
Строго
говоря,
масштаб
постоянен только на планах
116.
На географических картах онменяется от места к месту и даже в
одной точке — по разным
направлениям, что связано с
переходом от сферической поверхности
планеты
к
плоскому
изображению. Поэтому различают
главный и частный масштабы карт.
117.
Главный масштаб показывает,во сколько раз линейные размеры на
карте уменьшены по отношению к
эллипсоиду или шару. Этот масштаб
подписывают на карте, но он
справедлив лишь для отдельных
линий и точек, где искажения
отсутствуют.
118.
Частный масштаб отражаетсоотношения размеров объектов на
карте и эллипсоиде (шаре) в данной
точке. Он может быть больше или
меньше главного.
119.
Искажения на географическихкартах тем больше, чем больше
изображаемая территория, а в
пределах, одной карты искажения
возрастают с удалением от точки или
линии нулевых искажений, причем
скорость нарастания меняется по
разным от них направлениям.
120.
Искажениеизображения,
выражающееся
в
переменности
масштаба
и
присуще
всем
картографическим проекциям.
Это
—
основное
свойство
проекций.
121.
Частныймасштаб
длин,
показывает
отношение
длины
бесконечно малого отрезка на карте
ds' к длине бесконечно малого
отрезка
ds
на
поверхности
эллипсоида или шара, а частный
масштаб площадей р передает
аналогичные
соотношения
бесконечно малых площадей.
122.
В общем случае чем мельчемасштаб картографического изображения
и
чем
обширнее
территория,
тем
сильнее
сказываются
различия
между
главным и частным масштабами.
123.
Проекцияустанавливает
однозначное соответствие между
геодезическими координатами точек
(широтой В и долготой L) и их
прямоугольными координатами (X и
Y) на карте. Уравнения проекций в
общей форме выглядят предельно
просто
X=f1(B, L);Y=f2(B, L).
124.
Конкретные реализации функцийf1 и f2 часто выражены довольно
сложными
математическими
зависимостями, их число бесконечно,
а
следовательно,
разнообразие
картографических
проекций
практически
неограниченно.
125.
Изображение семейств линиймеридианов и параллелей в проекции называется картографической
сеткой. Эта сетка будет иметь
наиболее
простой
вид,
если
проекция описывается уравнениями
x f1 ( )
y f 2 ( ) ,
126.
в этом случае и параллели имеридианы изображаются взаимно
перпендикулярными прямыми.
Если
x f1 ( ), a y f 2 ( ; ),
то параллели изображаются прямыми линиями, параллельными оси
Y, а меридианы кривыми.
127.
x f1 ( ; ), a y f 2 ( )Если,
то меридианы будут прямыми, параллельными оси X, а параллели —
кривыми.
x f1 ( ; ), a y f 2 ( ; )
Если ,
то можно получить проекции с
разнообразными картографическими
сетками, вид которых зависит от f1 и
f2.
128.
Исходная аксиома при изысканиилюбых картографических проекций
состоит в том, что сферическую
поверхность
земного
шара
(эллипсоида,
глобуса)
нельзя
развернуть на плоскости карты
без
искажений.
Неизбежно
возникают деформации — сжатия и
растяжения, различные по величине
и направлению.
129.
Естькарты,
на
которых
Гренландия
больше
Южной
Америки, хотя, в действительности,
она меньше ее в восемь с лишним
раз, а Антарктида иногда вообще
занимает
весь
юг
карты.
Искажаются не только размеры, но и
формы объектов.
130.
контур Россиив трех разных
проекциях
131.
В картографических проекцияхмогут присутствовать следующие
виды искажений:
- искажения длин — вследствие
этого масштаб карты непостоянен в
разных точках и по разным
направлениям, а длины линий и
расстояния искажены;
132.
- искажения площадей —масштаб площадей в разных точках
карты различен, что является
прямым следствием искажений длин
и нарушает размеры объектов;
- искажения углов — углы между
направлениями на карте искажены
относительно тех же углов на
местности;
133.
искажения форм — фигуры накарте деформированы и не подобны
фигурам на местности, что прямо
связано с искажениями углов.
Любая
бесконечно
малая
окружность на шаре (эллипсоиде)
предстает на карте бесконечно
малым эллипсом — его называют
эллипсом искажений.
134.
Эллипс искаженийа — направление наибольшего растяжения масштаба;
в— направление наибольшего сжатия масштаба;
т — масштаб по меридиану; п — масштаб по параллели
135.
Его размеры и форма отражаютискажения длин, площадей и углов,
а ориентировка большой оси
относительно меридиана и параллели
—
направление
наибольшего растяжения.
Для оценки достоинств проекции
используют показатели искажения
площадей
р
и
углов
.
136.
Вычисление этих величин дляряда точек картографической сетки и
последующее проведение по ним
изокол (линий, соединяющих точки с
одинаковыми значениями искажений
площадей и углов), во-первых, дает
наглядную картину распределения
искажений, во-вторых, позволяет
учитывать
искажения
при
пользовании картой.
137.
Внормальных
конических
проекциях
—
параллельно
параллели касания (или параллелям
сечения);
в нормальных азимутальных
проекциях изоколы параллельны
концентрическим
окружностям
параллелей;
138.
в нормальных цилиндрическихпроекциях изоколы располагаются
параллельно
экватору
(или
параллелям сечения).
Очевидно,
нормальные
цилиндрические
проекции
целесообразно
применять
для
изображения экваториальной зоны и
вообще территорий, вытянутых вдоль
экватора.
139. Изоколы площадей в равноугольной цилиндрической проекции
140.
Нормальныеконические
проекции — для территорий,
лежащих в средних широтах и
вытянутых с востока на запад
(например, для бывшей СССР).
Нормальные
азимутальные
проекции — для полярных районов.
141.
Такжелегко
представить
расположение изокол в поперечных
и косых проекциях, в поперечной
цилиндрической проекции изоколы
параллельны меридиану касания и,
следовательно,
такие проекции
выгодны для передачи территорий,
вытянутых вдоль этого меридиана с
севера на юг.
142.
В любой азимутальной проекцииизоколы
образуют
окружности,
концентрические относительно точки
касания
плоскости;
поэтому
азимутальные проекции удобны для
территорий округлой формы (при
центральном
положении
точки
касания). В некоторых проекциях
изоколы
могут
образовывать
сложную систему кривых линий .
143. Стереографическая проекция с изоколами площадей
144. Равновеликая азимутальная проекция с изоколами углов
145. Задание на СРС 4
Формирование представлений офигуре Земли.
Геоид — фигура Земли. Уровенная
поверхность
Градусные измерения Эратосфена.
Размеры Земли.
Глобус — модель Земли.
146. Задание СРС5:
Каков вид нормальных сеток азимутальных,псевдоазимутальных
и
полиазимутальных
проекций?
2. Каков
вид нормальных сеток конических,
псевдоконических и поликонических проекций?
3. Каков вид нормальных сеток цилиндрических,
псевдоцилиндрических и полицилиндрических
проекций?
4. Какие
проекции называют обобщенными
азимутальными,
коническими
или
цилиндрическими?
1.
147. Литература
5 Берлянт А.М. Картография. – М.:Аспект Пресс, 2001, 2002. 336с.
6 Картоведение: Учебник для вузов/
А.М. Берлянт, А.В. Востокова,
В.И.Кравцова и др.: Под ред.
А.М.Берлянта – М.: Аспект Пресс,
2003. - 477с. (серия «Классический
университетский учебник»)

















































































































































 География
География








