Похожие презентации:
Этапы изучения математических предложений
1.
Этапы изучения математическихпредложений
Введение –
ситуация для «открытия» новой теоремы,
самостоятельной формулировки нового определения,
аксиомы, либо подготовка к их пониманию.
Усвоение
сводится к тому, чтобы учащиеся научились
применять определения, аксиомы, теоремы, быстро и
безошибочно запомнили их, понимали каждое слово в их
формулировках.
Закрепление
– осуществляется на последующих уроках
и сводится к повторению формулировок и отработке
навыков применения к решению задач.
2.
Введение математическихпредложений
1способ - Учащиеся подготавливаются к самостоятельному
формулированию определения, аксиомы, к «открытию»
теоремы.
2способ – Учащиеся готовятся к сознательному восприятию,
к пониманию нового предложения, формулировка которого
им сообщается затем в готовом виде.
Эвристический метод (метод целесообразных задач)
3способ - Учитель сам формулирует новые определения,
аксиомы, теоремы без какой-либо предварительной
подготовки, а затем сосредотачивает усилия учащихся на их
усвоении и закреплении.
3.
Введение математическихпредложений . Упражнения.
Определение
вписанного
угла
«Открытие»
теоремы о
диаметре
перпендикулярном
хорде
Диаметр окружности,
перпендикулярный хорде,
делит эту хорду пополам
4.
Введение математическихпредложений . Упражнения.
Определение вписанного угла
- Через точку окружности
проведите две хорды.
- Вы получили угол, который
называется вписанным.
- Дайте его определение.
- Постройте угол вершина
которого лежит на
окружности, а стороны
пересекают окружность.
- Полученный угол
называется вписанным.
- Дайте его определение
5.
Введение математическихпредложений . Упражнения.
Открытие теоремы о диаметре,
перпендикулярном хорде.
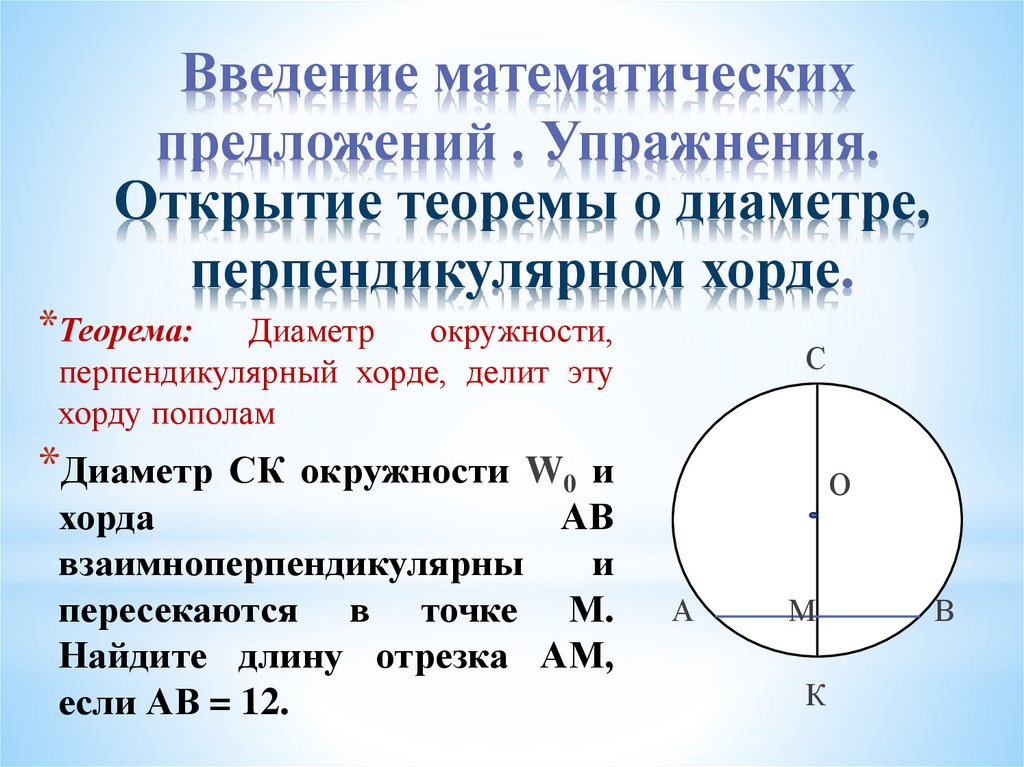
*Теорема:
Диаметр
окружности,
перпендикулярный хорде, делит эту
хорду пополам
С
*Диаметр
СК окружности W0 и
хорда
АВ
взаимноперпендикулярны
и
пересекаются в точке М.
Найдите длину отрезка АМ,
если АВ = 12.
О
А
М
К
В
6.
Методы усвоенияРаздельный-
когда процесс запоминания определения и
формирования навыков его применения протекают раздельно.
Компактный
– когда математическое предложение
читается по частям и по ходу чтения одновременно
выполняют упражнения.
Комбинация
методов
раздельного
Алгоритмический
заменяется алгоритмом.
–
и
компактного
математическое
предложение
7.
Методы усвоенияБиссектриса угла
Луч,
выходящий из вершины угла
и делящий его на две равные части,
называется биссектрисой угла
8.
Методы усвоенияПараллельность прямой и плоскости
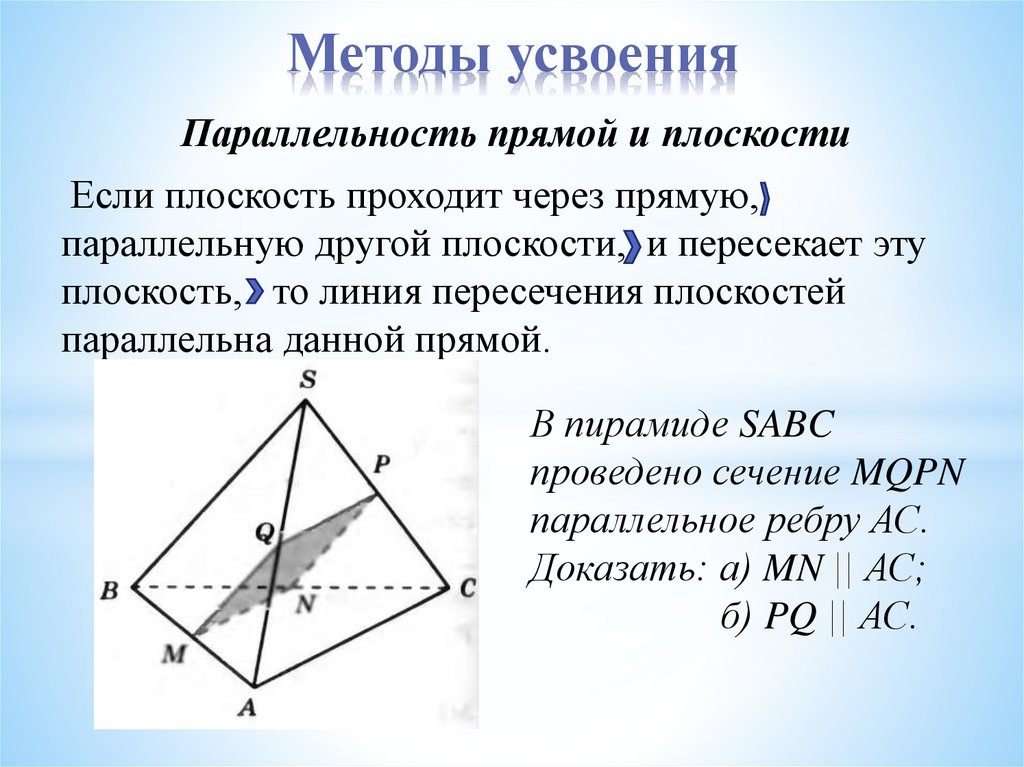
Если плоскость проходит через прямую,
параллельную другой плоскости, и пересекает эту
плоскость, то линия пересечения плоскостей
параллельна данной прямой.
В пирамиде SABC
проведено сечение MQPN
параллельное ребру АС.
Доказать: а) MN || АС;
б) PQ || АС.
9.
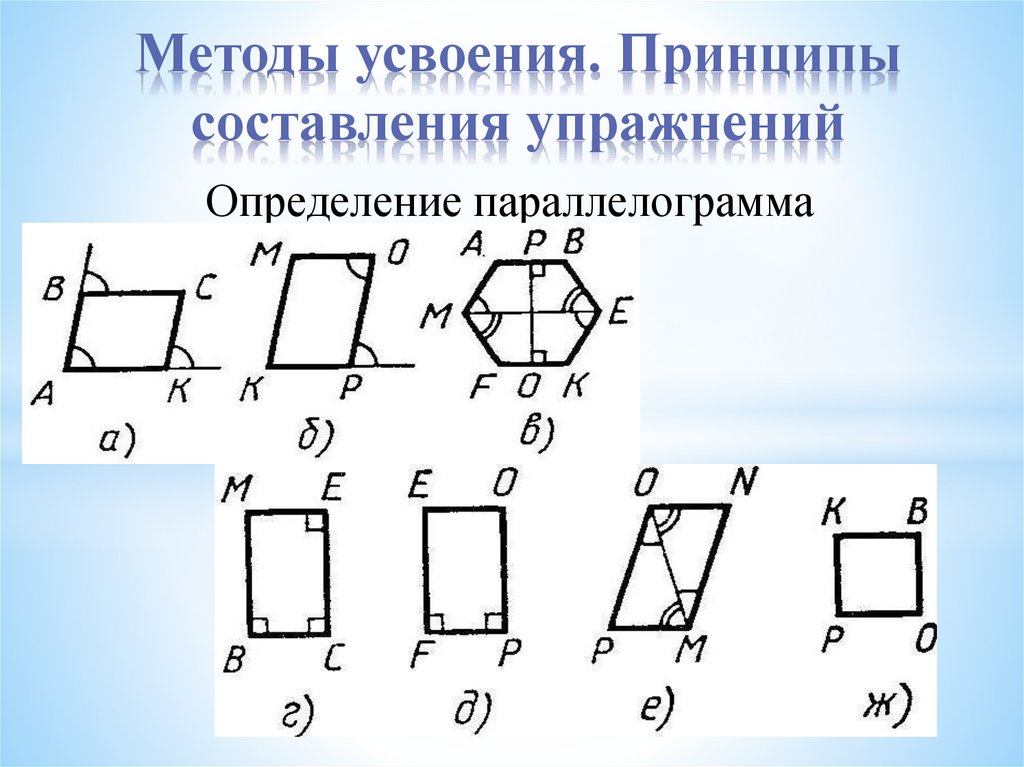
Методы усвоения. Принципысоставления упражнений
Определение параллелограмма
10.
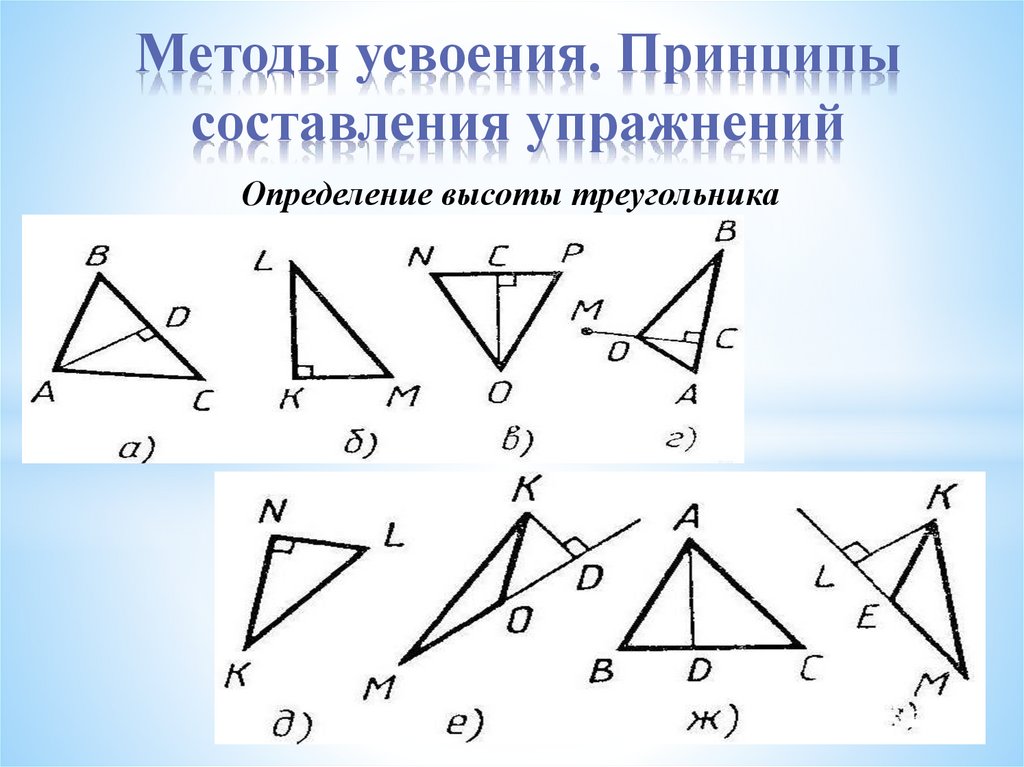
Методы усвоения. Принципысоставления упражнений
Определение высоты треугольника
11.
Методы усвоения. Принципысоставления упражнений
Определение
смежных
углов
Определение
трапеции
12.
Методы усвоения. Принципысоставления упражнений
Определение смежных углов
13.
Методы усвоения. Принципысоставления упражнений
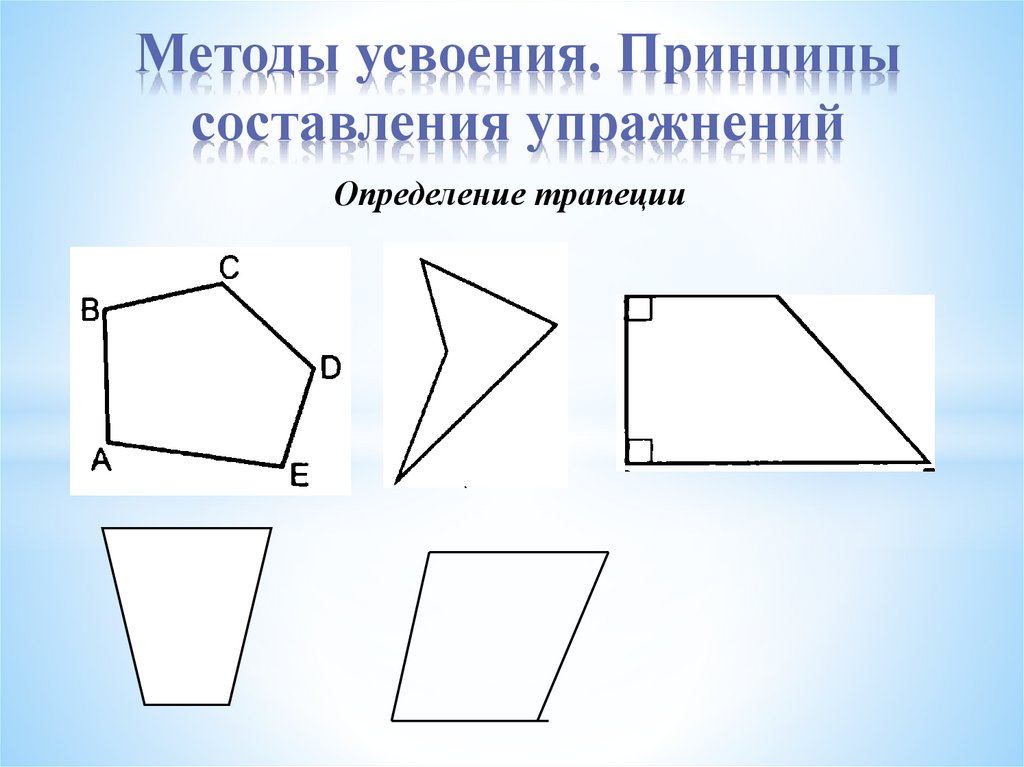
Определение трапеции
14.
Методы усвоения. Принципысоставления упражнений
Однотипность;
Непрерывного повторения;
Контрпримеры;
Сравнения;
Полноты;
Доступности и др.
15.
Приёмы закрепленияматематических предложений
I
-
формулировка определений,
встречающихся по ходу решения задач;
аксиом,
теорем,
II
- формулировка определений, аксиом, теорем, во время
фронтального опроса, проверить помнят ли;
III -
во время фронтального опроса сопровождая примером
или контрпримером с демонстрацией классу;
IV - отработка нескольких из перечня формулировок;
V-
во время фронтального опроса предлагаю упражнения в
которых требуется применение формулировки.
16.
Определения и поясняющиеописания
Определение – это такое математическое предложение, в
котором определяемое понятие сводится к ранее введенным
понятиям.
Часть прямой, ограниченная двумя точками, называется
отрезком.
Поясняющее описание – легко понятное, доступное
учащимся предложение, которое вызывает у всех учащихся
один и тот же наглядный образ и помогает хорошо усвоить
новое понятие.
Многогранник. Призма
17.
«рабочие» и «нерабочие»формулировки
Определения должны быть доступными для учащихся и
удобными в применении, поэтому:
•некоторые определения возможно заменять поясняющими
описаниями;
•теоремы «разъединять» В
параллелограмме
противоположные
стороны
и
противоположные углы равны
•изменять последовательность указаний в правиле прежде поставить знак результата, а потом складывать,
умножать и т.д. модули чисел, а не наоборот, как
рекомендуют учебники.
18.
1признак равенстватреугольников
Введение – «открытие» теоремы
Закрепление – во время
фронтального опроса, сопровождая
примером или контрпримером с
демонстрацией классу.
Усвоение – комбинация раздельного
и компактного метода
19.
ПризмаПризма
Прямая призма














 Математика
Математика








